Заряды равносторонний треугольник потенциал

Чертов А. Г., Воробьев А. А. Задачник по физике: Учебное пособие для вузов. 7 изд., 2001 г.

• версия для печати
• Войдите или зарегистрируйтесь, чтобы отправлять комментарии

Комментарии

В центре треугольника напряженность равна геометрической сумме напряженностей, создаваемых зарядами 1, 2 и 3.

Заряды по модулю равны, поэтому:

E₁ = E₂ = E₃ = 3k|q| / a 2 , так как a(√3) / 3 — расстояние от вершины треугольника до центра треугольника О.

Напряженность поля в точке О: E = E₃ + E₁ cos 60° + E₂ cos 60° = 2E₁ = 6k|q| / a 2 .

Потенциал в точке O равен алгебраической сумме потенциалов, создаваемых зарядами 1, 2 и 3:

В двух вершинах равностороннего треугольника со стороной

Задача. В двух вершинах равностороннего треугольника со стороной длиной см находятся два заряда, модули которых нКл. Определите потенциал поля в третьей вершине треугольника, если: a) оба заряда положительные; b) оба заряда отрицательные; c) заряды противоположных знаков.

Дано:

Решение

Думаем: источником электростатического поля в задаче являются точечные заряды, тогда для потенциала точечного заряда:

Т.к. зарядов несколько,, то для поиска общих параметров системы будем использовать принцип суперпозиции для потенциала (полный потенциал, создаваемый в точке равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в этой точке):

Решаем: для визуализации системы нарисуем её (рис. 1).

Рис. 1. Система зарядов для поиска потенциала

Точка А — точка, где по нашему условию нужно найти потенциал. Каждый из зарядов создаёт свой потенциал в искомой точке, который мы можем найти из (1):

Тогда, исходя из (2), получим общий потенциал в точке A:

А теперь адаптируем получившееся соотношение (5) под условия задачи. Разница в условиях задачи по пунктам состоит в том, что значения зарядов различные.

a) в случае 0″ title=»displaystyle <_>=<_>>0″ data-lazy-src=»https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%7B%7Bq%7D_%7B1%7D%7D%3D%7B%7Bq%7D_%7B2%7D%7D%3E0&is-pending-load=1#038;bg=ffffff&fg=000000&s=0″ srcset=»data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7″>:

Считаем: вспоминаем константы Н*м /Кл , И не забываем перевести все параметры (расстояния) в единицы СИ.

Принцип суперпозиции сил и полей

теория по физике 🧲 электростатика

Принцип суперпозиции сил

Результирующая, или равнодействующая, сила равна векторной сумме всех сил, действующих на тело:

F_i— сила, с которой электрическое поле зарядом q действует на пробный заряд q_i, помещенный в это поле на расстоянии r_iот этого заряда. Численно ее можно вычислить по формуле:

F i = k q i q r 2 i . .

Алгоритм решения задач на определение равнодействующей силы (точечный заряд находится в поле, созданном другими точечными зарядами):

1. Сделать чертеж. Указать расположение всех зарядов и их знаки.
2. Выделить заряд, для которого определяют равнодействующую.
3. Пронумеровать остальные заряды.
4. Определить расстояния от выделенного заряда до всех остальных.
5. Построить все силы, действующие на интересующий нас заряд. При этом необходимо учитывать знаки зарядов, их модули и расстояния между зарядами.
6. Найти геометрическую (векторную) сумму всех сил, действующих на выделенный заряд.
7. Пользуясь формулами геометрии и законом Кулона, определить модуль равнодействующей.

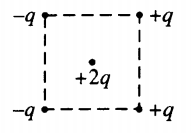
Пример №1. Как направлена (вправо, влево, вверх, вниз) кулоновская сила − F K , действующая на положительный точечный электрический заряд +2q, помещенный в центр квадрата, в вершинах которого находятся заряды +q, +q, –q, –q?

Известно, что одноименные заряды отталкиваются, а разноименные – притягиваются. Из рисунка видно, что заряд +2q, находящийся в центре квадрата, будет отталкиваться от зарядов +q, находящихся справа, и будет притягиваться к зарядам –q, находящимся слева.

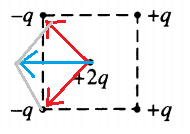
Сила Кулона обратно пропорциональна квадрату расстояния между зарядами, то есть с увеличением расстояния r убывает по квадратическому закону. Так как заряд +q находится точно в центре квадрата, то расстояния от зарядов +q, +q, -q, -q будут равны, следовательно, равна по модулю и сила Кулона, действующая на заряд +2q. Суперпозиция сил, действующих на заряд +2q:

Из рисунка видно, что кулоновская сила − F K , действующая на положительный точечный электрический заряд +2q, направлена влево.

Принцип суперпозиции полей

Если в некоторой точке пространства складываются электрические поля от нескольких зарядов, то результирующая напряженность находится как векторная сумма напряженностей отдельных полей:

− E i — напряженность, создаваемая зарядом q i в точке, находящейся на расстоянии r i :

− E i = k q i r 2 i . .

Векторное сложение напряженностей аналогично нахождению равнодействующей сил Кулона, только в интересующую нас точку пространства помещают положительный пробный заряд. Чтобы найти результирующий потенциал в точке, необходимо алгебраически сложить потенциалы всех полей. Нельзя забывать, что знак потенциала определяется знаком заряда, создающим электрическое поле:

φ i — потенциал электростатического поля, создаваемого зарядом q i на расстоянии r i от него. Численно он равен:

φ i = ± k q i r i . .

Для определения полной энергии надо сложить потенциальные энергии всех пар зарядов:

W i p — потенциальная энергия взаимодействия зарядов q i и q n , находящихся на расстоянии r i друг от друга. Численно она равна:

W i p = ± k q i q n r i . .

Примеры определения расстояний

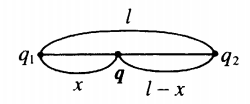Два заряда лежат на одной прямой на расстоянии l друг от друга. Изучаемый заряд лежит между ними:

r 1 = x ; r 2 = l − x

Изучаемый заряд лежит в вершине квадрата со стороной a:

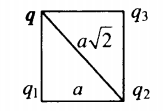
r 1 = r 3 = a ; r 2 = a √ 2

Изучаемый заряд лежит в центре равностороннего треугольника со стороной a:

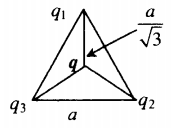
r 1 = r 2 = r 3 = a √ 3 . .

Изучаемый заряд лежит в вершине прямоугольника со сторонами a и b:

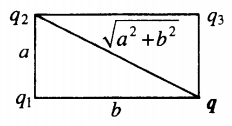
r 1 = b ; r 2 = √ a 2 + b 2 ; r 3 = a

Изучаемый заряд лежит в точке пересечения диагоналей ромба со стороной a. Угол при вершине ромба 120 о :

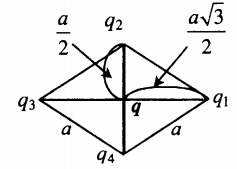
r 1 = r 3 = a √ 3 2 . . ; r 2 = r 4 = a 2 . .

Изучаемый заряд лежит в центре правильного шестиугольника со стороной a:

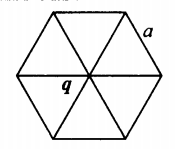
r 1 = r 2 = r 3 = r 4 = r 5 = r 6 = a

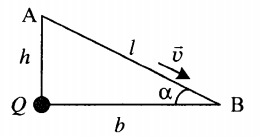
Пример №2. Маленький заряженный шарик массой m, имеющий заряд q, движется с высоты h по наклонной плоскости с углом наклона α. В вершине прямого угла, образованного высотой и горизонталью, находится неподвижный заряд Q. Какова скорость шарика у основания наклонной плоскости v, если его начальная скорость равна нулю? Трением пренебречь.

Применим закон сохранения энергии, согласно которому полная энергия шарика в точке А равна полной энергии шарика в точке В (трением пренебрегаем):

Полная энергия шарика с зарядом qв точке А равна сумме его механической потенциальной энергии и потенциальной энергии взаимодействия с зарядом Q:

E A = m g h + k q Q h . .

В точке В механическая потенциальная энергия шарика равна нулю, но в этой точке максимальная его кинетическая энергия. Полная энергия шарика в точке В равна:

E B = m v 2 2 . . + k q Q b . .

Расстояние между точкой В и местом, где находится заряд Q:

Приравняем правые части уравнений:

m g h + k q Q h . . = m v 2 2 . . + k q Q b . .

m g h + k q Q h . . = m v 2 2 . . + k q Q tan . α h . .

m v 2 2 . . = m g h + k q Q h . . − k q Q tan . α h . . = m g h + k q Q h . . ( 1 − tan . α )

v =   .  ⎷ 2 ( m g h + k q Q h . . ( 1 − tan . α ) ) m . . = √ 2 g h + 2 k Q m h . . ( 1 − tan . α )

Точка В находится в середине отрезка АС. Неподвижные точечные заряды + q и −2q расположены в точках А и С соответственно (см. рисунок). Какой заряд надо поместить в точку С взамен заряда −2q, чтобы напряжённость электрического поля в точке В увеличилась в 2 раза?

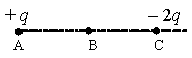
💥 Видео