Треугольник, вписанный в окружность. Теорема синусов
 Серединный перпендикуляр к отрезку Серединный перпендикуляр к отрезку |
 Окружность описанная около треугольника Окружность описанная около треугольника |
 Свойства описанной около треугольника окружности. Теорема синусов Свойства описанной около треугольника окружности. Теорема синусов |
 Доказательства теорем о свойствах описанной около треугольника окружности Доказательства теорем о свойствах описанной около треугольника окружности |
- Серединный перпендикуляр к отрезку
- Окружность, описанная около треугольника
- Свойства описанной около треугольника окружности. Теорема синусов
- Доказательства теорем о свойствах описанной около треугольника окружности
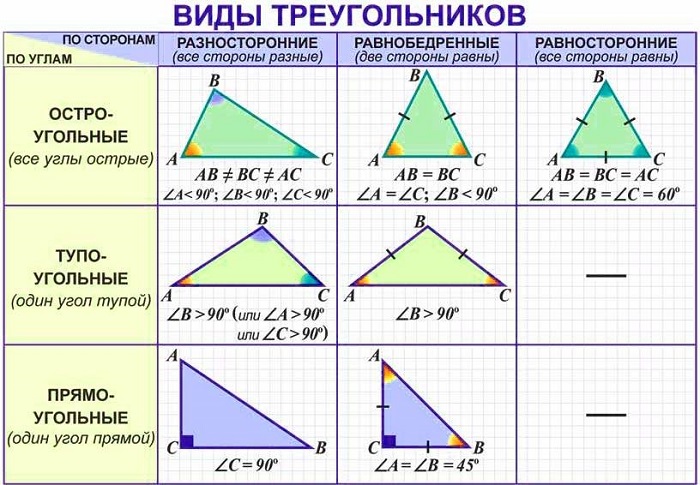
- Остроугольный треугольник — виды, свойства и признаки
- Виды, признаки и свойства остроугольных треугольников
- Равносторонний треугольник
- Разносторонний треугольник
- Равнобедренный остроугольный треугольник
- Равнобедренный тупоугольный треугольник
- Треугольник описанный около окружности
- Определение
- Формулы
- Радиус вписанной окружности в треугольник
- Радиус описанной окружности около треугольника
- Площадь треугольника
- Периметр треугольника
- Сторона треугольника
- Средняя линия треугольника
- Высота треугольника
- Свойства
- Признаки существования
- Признаки равенства
- Термины
- 🎥 Видео
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Серединный перпендикуляр к отрезку
Определение 1 . Серединным перпендикуляром к отрезку называют, прямую, перпендикулярную к этому отрезку и проходящую через его середину (рис. 1).
Теорема 1 . Каждая точка серединного перпендикуляра к отрезку находится на одном и том же расстоянии от концов этого отрезка.
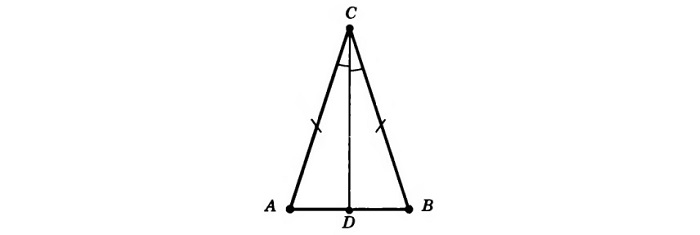
Доказательство . Рассмотрим произвольную точку D , лежащую на серединном перпендикуляре к отрезку AB (рис.2), и докажем, что треугольники ADC и BDC равны.
Действительно, эти треугольники являются прямоугольными треугольниками, у которых катеты AC и BC равны, а катет DC является общим. Из равенства треугольников ADC и BDC вытекает равенство отрезков AD и DB . Теорема 1 доказана.
Теорема 2 (Обратная к теореме 1) . Если точка находится на одном и том же расстоянии от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.
Доказательство . Докажем теорему 2 методом «от противного». С этой целью предположим, что некоторая точка E находится на одном и том же расстоянии от концов отрезка, но не лежит на серединном перпендикуляре к этому отрезку. Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точки E и A лежат по разные стороны от серединного перпендикуляра (рис.3). В этом случае отрезок EA пересекает серединный перпендикуляр в некоторой точке, которую мы обозначим буквой D .
Докажем, что отрезок AE длиннее отрезка EB . Действительно,
Таким образом, в случае, когда точки E и A лежат по разные стороны от серединного перпендикуляра, мы получили противоречие.
Теперь рассмотрим случай, когда точки E и A лежат по одну сторону от серединного перпендикуляра (рис.4). Докажем, что отрезок EB длиннее отрезка AE . Действительно,
Полученное противоречие и завершает доказательство теоремы 2
Видео:№711. Начертите три треугольника: тупоугольный, прямоугольный и равносторонний. ДляСкачать

Окружность, описанная около треугольника
Определение 2 . Окружностью, описанной около треугольника , называют окружность, проходящую через все три вершины треугольника (рис.5). В этом случае треугольник называют треугольником, вписанным в окружность, или вписанным треугольником .
Видео:№701. Начертите три треугольника: остроугольный, прямоугольный и тупоугольный. В каждыйСкачать

Свойства описанной около треугольника окружности. Теорема синусов
| Фигура | Рисунок | Свойство | |
| Серединные перпендикуляры к сторонам треугольника |  | Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке. Посмотреть доказательство | |
| Окружность, описанная около треугольника |  | Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника. Посмотреть доказательство | |
| Центр описанной около остроугольного треугольника окружности | Центр описанной около остроугольного треугольника окружности лежит внутри треугольника. | ||
| Центр описанной около прямоугольного треугольника окружности |  | Центром описанной около прямоугольного треугольника окружности является середина гипотенузы. Посмотреть доказательство | |
| Центр описанной около тупоугольного треугольника окружности |  | Центр описанной около тупоугольного треугольника окружности лежит вне треугольника. | |
| Теорема синусов |  | ||
| Площадь треугольника |  | ||
| Радиус описанной окружности |  |
| Серединные перпендикуляры к сторонам треугольника |
 |
Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.

Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.

Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.

Центром описанной около прямоугольного треугольника окружности является середина гипотенузы.

Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.

Для любого треугольника справедливы равенства (теорема синусов):

где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности.

Для любого треугольника справедливо равенство:
где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности.

Для любого треугольника справедливо равенство:
где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности.
Видео:Построить описанную окружность (Задача 1)Скачать

Доказательства теорем о свойствах описанной около треугольника окружности
Теорема 3 . Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.
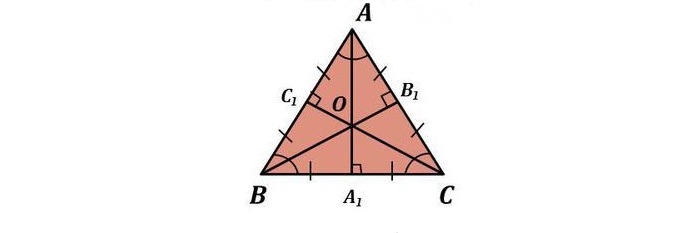
Доказательство . Рассмотрим два серединных перпендикуляра, проведённых к сторонам AC и AB треугольника ABC , и обозначим точку их пересечения буквой O (рис. 6).
Поскольку точка O лежит на серединном перпендикуляре к отрезку AC , то в силу теоремы 1 справедливо равенство:
Поскольку точка O лежит на серединном перпендикуляре к отрезку AB , то в силу теоремы 1 справедливо равенство:
Следовательно, справедливо равенство:
откуда с помощью теоремы 2 заключаем, что точка O лежит на серединном перпендикуляре к отрезку BC. Таким образом, все три серединных перпендикуляра проходят через одну и ту же точку, что и требовалось доказать.
Следствие . Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.
Доказательство . Рассмотрим точку O , в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника ABC (рис. 6).
При доказательстве теоремы 3 было получено равенство:
из которого вытекает, что окружность с центром в точке O и радиусами OA , OB , OC проходит через все три вершины треугольника ABC , что и требовалось доказать.
Теорема 4 (теорема синусов) . Для любого треугольника (рис. 7)

Доказательство . Докажем сначала, что длина хорды окружности радиуса R хорды окружности радиуса R , на которую опирается вписанный угол величины φ , вычисляется по формуле:
| l = 2Rsin φ . | (1) |
Рассмотрим сначала случай, когда одна из сторон вписанного угла является диаметром окружности (рис.8).
Поскольку все вписанные углы, опирающиеся на одну и ту же дугу, равны, то для произвольного вписанного угла всегда найдется равный ему вписанный угол, у которого одна из сторон является диаметром окружности.
Формула (1) доказана.
Из формулы (1) для вписанного треугольника ABC получаем (рис.7):
Видео:Строим вписанную в данный треугольник окружность (Задача 2).Скачать

Остроугольный треугольник — виды, свойства и признаки
Одна из центральных тем на уроках геометрии – остроугольный треугольник, составная часть своих более сложных аналогов и иных тригонометрических форм.
Азы изучения точной науки начинаются с рассмотрения уникальной комбинации из трех сторон и острых углов.
Видео:32. Остроугольный, прямоугольный и тупоугольный треугольникиСкачать

Виды, признаки и свойства остроугольных треугольников
Трехсторонние фигуры разделяются на множество подвидов и категорий.
Общая классификация по наибольшему углу делит их на 3 группы:
Они располагают как общими для формы с тремя сторонами характеристиками, так и специфическими признаками.
3 угла, сумма которых равна 180°, (величина каждого меньше 90°) и 3 стороны;
сумма длин любых двух сторон больше оставшейся третьей.
Свойства остроугольной фигуры определяются вспомогательными геометрическими линиями, всегда находящимися внутри него:
1. Биссектрисы, делящие углы пополам, являются центром, вокруг которого можно нарисовать вписанную окружность.
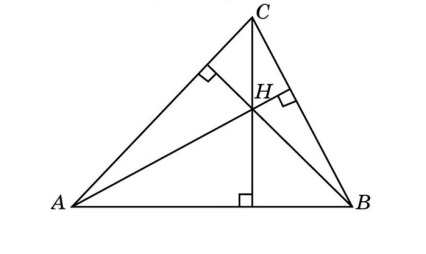
2. Высоты пересекаются в одной точке, образуя ортоцентр.
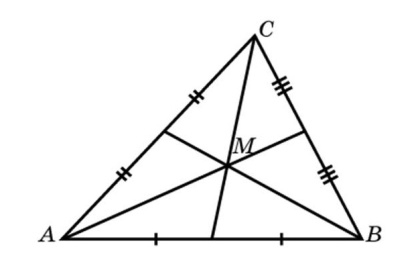
3. Медианы в точке пересечения пролегают в пропорции 2:1 (2 трети до центра и 1 треть после).
Уникальные особенности зависят от разновидностей фигуры.
Видео:7 класс, 32 урок, Остроугольный, прямоугольный и тупоугольный треугольникиСкачать

Равносторонний треугольник
«Идеальный» правильный треугольник, облегчающий решение задач. Определение, форма и свойства данной геометрической формы исходят из названия — все углы равны 60°, а стороны равны друг другу.
Полное равенство придает и другую особенность: медианы, биссектрисы и высоты полностью совпадают.
Видео:Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

Разносторонний треугольник
Наиболее часто встречаемый на чертежах в геометрии вариант, один из самых трудноразрешимых видов. Разносторонними бывают и прямоугольные, и тупоугольные фигуры.
Уникальных отличий не имеет, только общие:
все параметры имеют разные значения;
совпадений между вспомогательными линиями нет.
Видео:Виды треугольниковСкачать

Равнобедренный остроугольный треугольник
Здесь при основании (стороне, не равной остальным) находятся равные друг другу 2 стороны и 2 угла. Выглядит как вытянутый в одну сторону равносторонний треугольник.
проведенная к основанию линия – и биссектриса, и высота, и медиана;
вспомогательные линии из крайних точек при основании совпадают.
Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Равнобедренный тупоугольный треугольник
Пусть он и называется равнобедренным, но из-за наличия угла более 90° не является остроугольным и является представителем другой группы.
Начертить его сложнее (рисунок следует начинать с основания и 2 острых углов и уже после создавать тупой), но процесс решения и изучения прост.
Отличие у него одно – точка пересечения двух высот, проведенных от углов при основании, выходит за периметр треугольника. Чтобы ее обозначить, необходимо нарисовать «продолжения» равнобедренных линий. Все остальные свойства совпадают.
В ключевых и фундаментальных разделах математики именно треугольник является основой для доказательства многих теорем и помощью в решении множества задач. Твердое знание его свойств откроет путь к успехам в расчетах, вычислениях, оформлении чертежей и фото в проектных работах.
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Треугольник описанный около окружности
Видео:Остроугольный треугольникСкачать
Определение
Треугольник, описанный около окружности — это треугольник,
который находится около окружности и соприкасается
с ней всеми тремя сторонами.
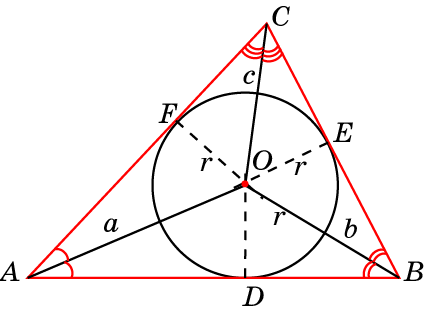
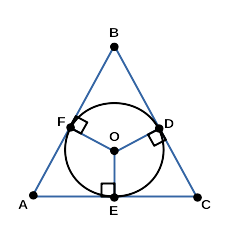
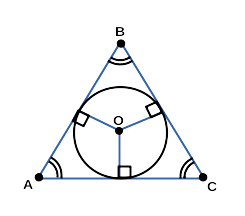
На рисунке ниже изображена окружность, вписанная в треугольник;
и треугольник, описанный около окружности.
△ ABC — треугольник, описанный около окружности;
A, B, C — вершины треугольника, описанного около окружности;
F, D, E — точки касания треугольника, описанного около окружности;
O — центр окружности, вписанной в треугольник;
OD = OF = OE — радиусы треугольника, описанного около окружности;
AB, BC, CA — касательные;
FA = AE, EC = CD, FB = BD — отрезки касательных;
OF ⟂ AB, OD ⟂ BC, OE ⟂ AC;
Треугольник ABC имеет три точки, где соприкасаются
стороны и сама окружность, эти точки называют точками
касания. У данного треугольника их всего три.
В любой треугольник можно вписать окружность, причем
только одну. Треугольник, в который вписана окружность
называется треугольником описанным около окружности.
Треугольники, описанные около окружности, обладают рядом
рядом отличительных свойств, характерных признаков, уникальными
терминами, а также формулам, по которым можно найти разные величины.
Формулы радиуса вписанной окружности, радиуса описанной окружности,
диаметра, средней линии, периметра, площади стороны позволяют выразить
одни величины через другие, рассчитать длину величины, узнать во сколько
раз одна величина отличается от другой, какая прослеживается взаимосвязь.
Длина любой величины произвольного
треугольника может измеряется в мм, см, м, км.
Видео:Высоты треугольника.Скачать

Формулы
Радиус вписанной окружности в треугольник
r — радиус вписанной окружности треугольника, описанного около окружности.
- Радиус вписанной окружности в треугольник,
если известна площадь и все стороны:
Радиус вписанной окружности в треугольник,
если известны площадь и периметр:
Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:
Радиус описанной окружности около треугольника
R — радиус описанной окружности треугольника, описанного около окружности.
- Радиус описанной окружности около треугольника,
если известна одна из сторон и синус противолежащего стороне угла:
Радиус описанной окружности около треугольника,
если известны все стороны и площадь:
Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:
Площадь треугольника
S — площадь треугольника, описанного около окружности.
- Площадь треугольника вписанного в окружность,
если известен полупериметр и радиус вписанной окружности:
Площадь треугольника вписанного в окружность,
если известен полупериметр:
Площадь треугольника вписанного в окружность,
если известен высота и основание:
Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:
Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:
[ S = fracab cdot sin angle C ]
Периметр треугольника
P — периметр треугольника, описанного около окружности.
- Периметр треугольника вписанного в окружность,
если известны все стороны:
Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:
Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:
Сторона треугольника
a — сторона треугольника, описанного около окружности.
- Сторона треугольника вписанного в окружность,
если известны две стороны и косинус угла между ними:
Сторона треугольника вписанного в
окружность, если известна сторона и два угла:
Средняя линия треугольника
l — средняя линия треугольника, описанного около окружности.
- Средняя линия треугольника вписанного
в окружность, если известно основание:
Средняя линия треугольника вписанного в окружность,
если известны две стороны, ни одна из них не является
основанием, и косинус угла между ними:
Высота треугольника
h — высота треугольника, описанного около окружности.
- Высота треугольника вписанного в окружность,
если известна площадь и основание:
Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:
[ h = b cdot sin alpha ]
Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:
Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Свойства
Свойства треугольника, описанного около окружности,
а также окружности, вписанной в треугольник, медиан,
высот, биссектрис, радиусов-перпендикуляров.
Свойство 1. Окружность, можно вписать
в любой треугольник, только один раз.
Свойство 2. Центр окружности, вписанной в треугольник —
точка пересечения биссектрис, центр окружности.
Свойство 3. Центр окружности, описанной около треугольника —
точка пересечения серединных перпендикуляров.
Свойство 4. Центры вписанной и описанной окружностей
равностороннего треугольника, описанного около
окружности совпадают, имеют одну общую точку.
Свойство 5. Отрезок, проведенный из центра треугольника,
описанного около окружности, к любой из сторон,
является радиусом.
Свойство 6. У любого треугольника центр
вписанной окружности находится только внутри.
Свойство 7. Окружность находящаяся внутри
треугольника, описанного около окружности,
касается всех его сторон.
Свойство 8. Вписанная окружность и треугольник,
описанный около окружности, имеют три общие точки,
которые лежат на трех сторонах треугольника.
Свойство 9. Формула радиуса вписанной окружности
у треугольника, описанного около окружности, и четырехугольника,
у которого суммы противоположных равны, совпадает.
Свойство 10. Радиус описанной около треугольника окружности,
можно выразить и рассчитать через Теорему Синусов.
Свойство 11. У треугольника, описанного около
окружности, радиус вписанной окружности, можно
рассчитать через площадь и полупериметр.
Свойство 12. Радиус в точку касания есть перпендикуляр.
Свойство 13. Окружность, вписанная в треугольник, разделяет
стороны треугольника на 3 пары равных отрезков.
Свойство 14. Стороны треугольника, описанного около
окружности, можно также называть касательными.
Свойство 15. Отрезки, которые проведены из центра вписанной
окружности, к точкам касания, перпендикулярны сторонам.
Свойство 16. Сумма углов треугольника, описанного
около окружности, равна 180 градусам.
Свойство 17. Центр вписанной окружности
равноудален от всех сторон треугольника.
Свойство 18. Центр вписанной в треугольник окружности в научных
кругах называется замечательной точкой треугольника, либо инцентром.
Свойство 19. Правильный треугольник, описанный около
окружности, имеет точки касания с окружность, в серединах сторон.
Свойство 20. Равнобедренный, прямоугольный, равносторонний
треугольники, описанные около окружности, в точке пересечения
биссектрис и центре окружности, имеют одну общую точку.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Признаки существования
Признак 1. Центр вписанной окружности —
это точка пересечения биссектрис.
Признак 2. На сторонах треугольника лежат
три точки касания вписанной окружности.
Признак 3. Вписанная окружность делит смежные
стороны треугольника на равные отрезки касательных.
Признак 4. У вписанной окружности три радиуса в точку касания быть перпендикулярами.
Исходя из вышеперечисленных признаков, исходных
данных, внешнего вида, можно определить является ли
треугольник описанным около окружности или же нет.
Видео:Виды треугольников: остроугольный, прямоугольный ,тупоугольный. Как начертить треугольникСкачать
Признаки равенства
Признак 1. По двум сторонам и углу между ними.
Если две стороны и угол между ними одного треугольника, описанного
около окружности, равны двум сторонам и углу между ними другого
треугольника, описанного около окружности, то такие треугольники равны.
Признак 2. По стороне и двум прилежащим к ней углам.
Если сторона и два прилежащих к ней угла одного треугольника, описанного
около окружности, равны стороне и двум прилежащим к ней углам другого
треугольника, описанного около окружности, то такие треугольники равны.
Признак 3. По трем сторонам.
Если три стороны одного треугольника, описанного
около окружности, равны трем сторонам другого
треугольника, описанного около окружности.
Как мы знаем, любой треугольник может быть описан около
окружности, исходя из этого можно сказать, что около
окружности, могут быть описаны следующие виды треугольников:
- Разносторонний треугольник
- Равносторонний / правильный треугольник
- Прямоугольный треугольник
- Равнобедренный треугольник
- Равнобедренныйпрямоугольный треугольник
- Прямоугольный треугольник, описанный около окружности
Характерные признаки: один из углов прямой,
длину сторон можно найти через Теорему
Пифагора, сумма острых углов 90 градусов.
Основные формулы:
- Равнобедренный треугольник, описанный около окружности
Характерные признаки: два угла равны,
две стороны равны, третий угол можно
найти зная два других.
Основные формулы:
- Равносторонний треугольник, описанный около треугольника
Основные формулы:
Видео:№16 из ЕГЭ2022 и олимпиады. Красивое доказательство свойства ортоцентра остроугольного треугольникаСкачать

Термины
Точка касания — это точка, где соприкасается вписанная
окружность с треугольником; это общая точка, для окружности
и треугольника, которая лежит на любой из сторон треугольника.
Инцентр — это точка, где пересекаются три биссектрисы
треугольника; это центр вписанной окружности в треугольник;
это одна из замечательных точек в геометрии.
Касательная — это сторона треугольника, которая имеет с
вписанной окружностью одну общую точку — точку касания.
Ортоцентр — точка, где пересекаются высоты треугольника.
Ось симметрии — это прямая, которая делит
треугольник на равные половины.
Замечательная точка — это точка пересечения медиан,
высот, биссектрис, серединных перпендикуляров.
Отрезок касательной — это отрезок, который берет начало
у одной из вершин треугольника, и имеет конец в точке касания.
🎥 Видео
Построение высоты в треугольникеСкачать

Окружность и треугольникСкачать

Точка O центр окружности описанной около остроугольного треугольникаСкачать