Треугольники с общей высотой (4 видео) | Курс школьной геометрии

Треугольники общего вида

Содержание

Треугольники общего вида.
Свойства медиан:
Свойства высот:
Прямоугольный треугольник и его свойства:
Некоторые свойства прямоугольного треугольника:
Соотношение между сторонами и углами в прямоугольном треугольнике:
Значения тригонометрических функций некоторых углов:
Тригонометрические тождества:
Подобие треугольников
Признаки подобия треугольников:
Теорема синусов
Теорема косинусов
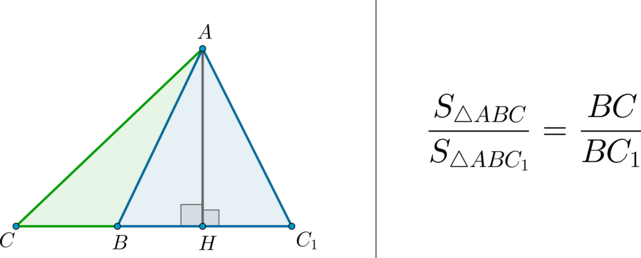
Отношение площадей треугольников, имеющих общую высоту (основание)
Основные свойства площадей треугольников
🌟 Видео

Видео:Какая из площадей больше? Треугольники с общей высотой. геометрия 8 классСкачать

Треугольники общего вида.

Основные свойства треугольников:

Сумма всех углов в треугольнике равна $180°$.
В равнобедренном треугольнике углы при основании равны.
В равнобедренном треугольнике высота, проведенная к основанию, одновременно является медианой и биссектрисой.
В равностороннем треугольнике все углы по $60°$.
Внешний угол треугольника равен сумме двух углов, не смежных с ним.
Средняя линия треугольника параллельна основанию и равна его половине.

$MN$ — средняя линия, так как соединяет середины соседних сторон.

Биссектриса — это линия, которая делит угол пополам.

В равнобедренном треугольнике биссектриса, проведённая из вершины к основанию, является также и медианой, и высотой.
Три биссектрисы в треугольнике пересекаются в одной точке, эта точка является центром вписанной в треугольник окружности.
Биссектрисы смежных углов перпендикулярны.
В треугольнике биссектриса угла делит противоположную сторону на отрезки, отношение которых такое же, как отношение сторон треугольника, между которыми эта биссектриса прошла.

Медиана — это линия, проведенная из вершины треугольника к середине противоположной стороны.

Свойства медиан:

1. Медиана делит треугольник на два равновеликих треугольника, т.е. на два треугольника, у которых площади равны.

2. Медианы пересекаются в одной точке и этой точкой делятся в отношении два к одному, считая от вершины.

3. В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы и радиусу описанной около этого треугольника окружности.

Высота в треугольнике — это линия, проведенная из вершины треугольника к противоположной стороне под углом в 90 градусов.

Свойства высот:

1. Три высоты (или их продолжения) пересекаются в одной точке.

2. Угол между высотами в остроугольном треугольнике равен углу между сторонами, к которым эти высоты проведены.

3. Высоты треугольника обратно пропорциональны его сторонам:

Прямоугольный треугольник и его свойства:

В прямоугольном треугольнике катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.

Некоторые свойства прямоугольного треугольника:

1. Сумма острых углов в прямоугольном треугольнике равна 90 градусов.

2. Катет прямоугольного треугольника, лежащий напротив угла в 30 градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)

3. Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности (R)

4. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями которых являются катеты данного треугольника.

5. В прямоугольном треугольнике радиус вписанной окружности равен: $r=/$ , где $а$ и $b$ – это катеты, $с$ – гипотенуза.

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$

Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.

Синусом (sin) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Косинусом (cos) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Тангенсом (tg) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Котангенсом (ctg) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения

Значения тригонометрических функций некоторых углов:

$α$	$30$	$45$	$60$
$sinα$	$/$	$/$	$/$
$cosα$	$/$	$/$	$/$
$tgα$	$/$	$1$	$√3$
$ctgα$	$√3$	$1$	$/$

Отношение площадей треугольников, имеющих общую высоту (основание)

Разделы: Математика

Цели урока:

Сформировать умение использовать формулу площади треугольника при решении задач;
Рассмотреть ключевые задачи об отношении площадей треугольников, имеющих общую высоту (основание). Познакомить учащихся с методами решения задач по теме.

Оборудование урока:

Компьютер.
Мультимедийный проектор.
Экран.

Раздаточный материал.

карточки с вопросами для опроса по домашнему заданию;
презентация к уроку (Приложение 1);
карточки для выполнения самостоятельной работы.

Этапы урока

Организационный момент.
Проверка домашнего задания (усвоение материала предыдущего урока)
Закрепление ранее изученного материала
Самостоятельная работа обучающего характера
Постановка домашнего задания.
Подведение итогов урока.

Ход урока

1. Организационный момент

Сообщаем тему урока. Поясняем важность рассматриваемого на уроке материала, говорим о том, что сведения последних уроков по площадям имеют широкое применение, сегодня на уроке используем их при решении задач.

Для эффективности работы в начале проверим домашнее задание и повторим изученный теоретический материал.

2. Проверка домашнего задания

Опрос учащихся у доски:

доказательство теоремы о площади ?.
доказательство следствий из неё
решение номеров домашнего задания.

В это время с классом работаем устно, по слайдам заранее подготовленной презентации.

3) Если AM=MC, то сравните площади этих треугольников.

Записать вывод в тетрадь:

Медиана делит треугольник на два равновеликих (равных по площади) треугольника, и площадь каждого из которых равна половине площади данного треугольника.

ВМ – медиана АВC

ВК – медиана АВМ

Найдите отношение площадей

5) Известно, что S_ABС=20см 2 (по условию предыдущего задания)

Чему равно отношение площадей двух треугольников, имеющих общее основание?

Записываем вывод в тетради:

Площади треугольников, имеющих общее основание, относятся как высоты, проведенные к основанию.

Далее заслушиваем и обсуждаем теоретические ответы учащихся по ДЗ.

3. Закрепление ранее изученного материала.

1. Выполняем задание №40 стр. 18-19 рабочей тетради по геометрии для 8 кл.

На рисунке точка М делит сторону АС АВС в отношении АМ : МС = 2 : 3

Площадь АВС равна 180 см 2 . Найдите площадь треугольника АВМ.

2. Решаем задачу №475 учебника.

Начертите АВС. Через вершину А проведите две прямые так, чтобы они разделили этот треугольник на три треугольника, имеющие равные площади.

Обсуждаем решение, используя слайды презентации

4. н/о (если позволяет время)

Данный параллелограмм разделите на три равновеликие части прямыми, выходящими из одной вершины.

Аналогично, ВВ₂ делит DВС на треугольники, имеющие одну высоту, их площади относятся как основания DB₂ : B₂C = 1 : 2 => Алгоритм построения: разделить каждую из сторон AD и DC параллелограмма в отношении 2 :1, считая от вершин А и С.

4. Самостоятельная работа обучающего характера

Вариант -1

1) СК – медиана АВС

S_СКВ = 32 см 2 . Найти S_ABС

2) S_КDM = 40 см 2

На стороне КМ отмечена точка А так, что КА : АМ = 2 :3

Вариант — 2

1) АМ – медиана АВС, площадь которого 48 см 2

Найти площадь АМС

2) S_DРК = 60 см 2

На стороне DК отмечена точка А так, что DА : АK = 3 :1

5. Постановка домашнего задания

Д.З. по учебнику стр. 124-125 № 473; 506; 511(а)

6. Подведение итогов урока

Литература

1. Геометрия 7-9. / Л.С. Атанасян, В.Ф. Бутузов и др./ “ Просвещение”, ОАО “Московский учебник”,М., 2008;

2. Рабочая тетрадь для 8 кл. об/об учреждений. Геометрия. / Атанасян Л.С. и др. / “Просвещение”, М, 2005;

2. Полонский В.Б., Рабинович Е.М., Якир М.С. / Геометрия: Задачник к школьному курсу М.: АСТ-ПРЕСС: Магистр-S, 1998.

Видео:Площади треугольников с равным углом.Скачать

Основные свойства площадей треугольников

Факт 1.
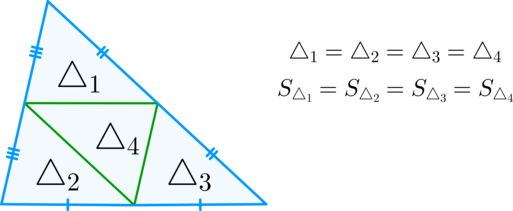
(bullet) Средние линии треугольника разбивают его на 4 равных треугольника.
Соответственно, площади этих треугольников равны.

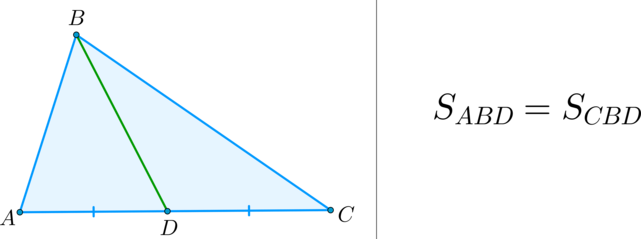
Факт 2.
(bullet) Медиана треугольника делит его на два треугольника, равных по площади (равновеликих).

Факт 3.
(bullet) Все 3 медианы треугольника делят его на 6 равновеликих треугольников.

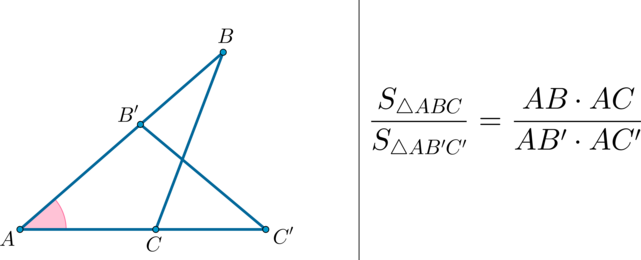
Факт 4.
(bullet) Площади треугольников, имеющих одинаковый угол, относятся как произведения сторон, образующих этот угол.

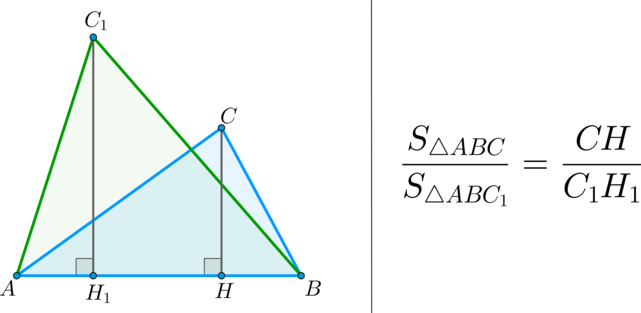
Факт 5.
(bullet) Площади треугольников, имеющих одинаковое основание, относятся как высоты, проведенные к этим основаниям.

Факт 6.
(bullet) Площади треугольников, имеющих одинаковую высоту, относятся как основания, к которым проведена эта высота.

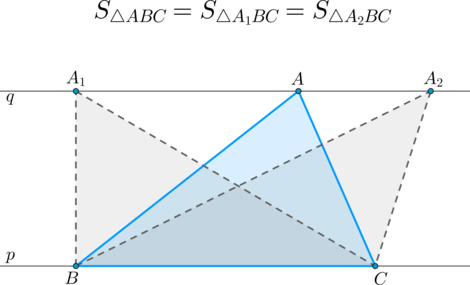
Факт 7.
(bullet) Если прямые (p) и (q) параллельны, то

Факт 8.
(bullet) Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
(bullet) Отношение периметров подобных треугольников равно коэффициенту подобия.