- Внутренние односторонние углы — теория, правило и свойства
- Углы по определению
- Доказательство теоремы
- Следствие из свойства прямых
- Построение параллелограмма
- Параллельность прямых
- Определение параллельности прямых
- Свойства и признаки параллельных прямых
- Задача 1
- Задача 2
- Углы при параллельных прямых и секущей. Вертикальные, смежные, односторонние, соответственные, накрест лежащие углы
- 🌟 Видео
Видео:Теорема 14.2 Если сумма односторонних углов равна 180 градусов, то прямые параллельны || Геометрия 7Скачать
Внутренние односторонние углы — теория, правило и свойства
Чтобы дать верное определение внутренним односторонним углам, нужно отличать их от вертикальных, смежных, соответственных и накрест лежащих. Их объединяет то, что они могут быть образованы двумя параллельными прямыми и пересекающей их линией. Утверждение о том, что сумма внутренних односторонних углов составляет 180 градусов, позволяет доказать теорему о параллельности прямых.
Видео:7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать
Углы по определению
Прямая, которая пересекает другие линии, идущие параллельно друг другу, образует не только внутренние, но и внешние углы. Один из них дополняет другой до 180 градусов. Это свойство можно доказать как для смежных, так и односторонних внутренних, каждый из которых имеет соответственный внешний.
Углы, расположенные на одной стороне от секущей, пересекающей 2 линии, идущие параллельно, называются накрест лежащими. Они отличаются от односторонних, образуя с ними смежные. В сумме они составляют 180 градусов.
Отрезок между линиями, проведенными параллельно между собой, можно обозначить AB. Если представить, что AB=0, то параллельные будут совпадать, а соответственные углы и односторонние станут смежными. Их сумма должна быть 180 градусов.
Видео:Параллельные прямые | Математика | TutorOnlineСкачать
Доказательство теоремы
Прямые являются параллельными, если сумма односторонних внутренних углов равна 180. Нужно доказать теорему по исходным данным. Секущая АВ является линией пересечения параллельных а и b.
Для доказательства теоремы можно допустить, что линии не являются параллельными, значит они пересекают друг друга в определенной точке С. Секущая АВ образует с а и b треугольник АВС, поскольку точка С лежит в одной из двух плоскостей относительно АВ. На линии а расположена сторона треугольника АС, а на b — ВС.
Если в противоположной полуплоскости отложить точку С1, то она образует с АВ другой треугольник АВС1. При этом по построению углы ВАС и АВС1 равны. Сумма САВ и СВА составляет 180, что указано в условии задачи. Следовательно, сторона АС1 принадлежит а, аналогично, ВС1 — линии b.
Точка пересечения С линий а и b принадлежит этим прямым. Вместе с тем точка С1 не может лежать на каждой из них, поскольку она находится в полуплоскости, где линии по построению не пересекаются.
Если в сумме односторонние углы составляют 180, то треугольника АВС1 не существует, значит а || b.
Видео:Пары углов в геометрииСкачать
Следствие из свойства прямых
На прямую а может быть опущен единственный перпендикуляр из любой точки А, которая не принадлежит данной линии. Доказательство утверждения состоит из следующих шагов:
Итак, отрезок АВ является единственным перпендикуляром, проходящим через точку А.
Видео:7 класс, 30 урок, Углы с соответственно параллельными или перпендикулярными сторонамиСкачать
Построение параллелограмма
Если односторонние углы не прямые, то один из них является острым, а другой — тупым, то есть меньшим или большим по величине. Если через каждый из них провести биссектрисы, то они должны пересечь противоположные стороны в определенных точках. Для этого достаточно отложить отрезки на параллельных линиях, равные AB, используя циркуль.
Секущая и отрезки, принадлежащие проведенным биссектрисам, образуют 2 треугольника вместе с параллельными. Напротив большего угла будет находиться биссектриса, отсекающая наибольший отрезок. Это подтверждает теорема о соотношении между углами и сторонами разностороннего треугольника.
Соединив точки пересечения биссектрис с параллельными прямыми, можно построить четырехугольник ABCD. Чтобы доказать, что полученная фигура является параллелограммом, достаточно учесть следующее:
Отложив от A и B равноудаленные точки C и D, можно получить линию CD, которая параллельна AB. Тогда CD — отрезок, перпендикулярный параллельным прямым BC и AD. Поскольку все отрезки полученной фигуры ABCD пересекаются перпендикулярно, то она является прямоугольником по построению.
Доказательство теоремы позволяет определять, какой является величина второго из двух внутренних односторонних углов при параллельных прямых и секущей. Решение задач по геометрии позволяет найти их градусную меру и в зависимости от разности между ними.
Видео:Углы при параллельных прямых и секущей. ОГЭ/ЕГЭ (часть 1)Скачать
Параллельность прямых
О чем эта статья:
10 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:7 класс. Глава4 - Параллельные прямые. сумма односторонних углов равна 180 градусовСкачать
Определение параллельности прямых
Начнем с главного — определимся, какие прямые параллельны согласно евклидовой геометрии. Мы недаром упомянули Евклида, ведь именно в его трудах, написанных за 300 лет до н. э., до нас дошли первые упоминания о параллельности.
Параллельными называются прямые в одной плоскости, не имеющие точек пересечения, даже если их продолжать бесконечно долго. Обозначаются они следующим образом: a II b.
Казалось бы, здесь все просто, но со времен Евклида над определением параллельных прямых и признаками параллельности прямых бились лучшие умы. Особый интерес вызывал 5-й постулат древнегреческого математика: через точку, которая не относится к прямой, в той же плоскости можно провести только одну прямую, параллельную первой. В XIX веке российский математик Н. Лобачевский смог опровергнуть постулат и указать на условия, при которых возможно провести как минимум 2 параллельные прямые через одну точку.
Впрочем, поскольку школьная программа ограничена евклидовой геометрией, вышеуказанное утверждение мы принимаем как аксиому.
На плоскости через любую точку, не принадлежащую некой прямой, можно провести единственную прямую, которая была бы ей параллельна.
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Видео:Углы при параллельных прямых и секущей | ЕГЭ 2023 Профильная математикаСкачать
Свойства и признаки параллельных прямых
Есть ряд признаков, по которым можно определить, что одна прямая параллельна другой. К счастью, свойства и признаки параллельности прямых тесно связаны, поэтому не придется запоминать много информации.
Начнем со свойств. Для этого проведем третью прямую, пересекающую параллельные прямые — она будет называться секущей. В результате у нас образуется 8 углов.
Если секущая проходит через две параллельные прямые, то:
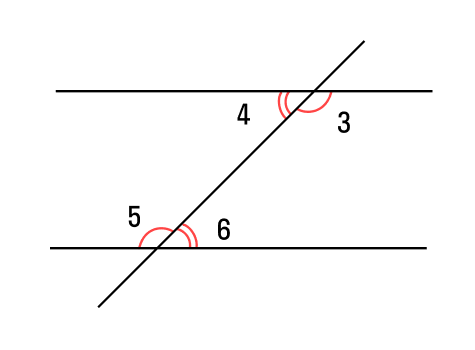
- два внутренних односторонних угла образуют в сумме 180°:
∠4 + ∠6 = 180°; ∠3 + ∠5 = 180°.
два внутренних накрест лежащих угла равны между собой:
два соответственных угла равны между собой:
∠1 = ∠5, ∠3 = ∠7, ∠4 = ∠8, ∠2 = ∠6.
Вышеуказанные свойства являются одновременно признаками, по которым мы можем сделать вывод о параллельности прямых. Причем достаточно установить и доказать лишь один признак — остальные будут к нему прилагаться.
А сейчас посмотрим, как все это помогает решать задачи и практиковаться в определении параллельности двух прямых.
Задача 1
Прямые MN и KP пересекают две другие прямые, образуя несколько углов. Известно, что ∠1 = 73°; ∠3 = 92°; ∠2 = 73°. Требуется найти величину ∠4.
Решение
Поскольку ∠1 и ∠2 являются соответственными, их равенство говорит о том, что MN II KP. Следовательно, ∠3 = ∠MPK = 92°.
Согласно другому свойству параллельных прямых ∠4 + ∠MPK = 180°.
Задача 2
Две параллельные прямые а и b удалены друг от друга на расстояние 27 см. Секущая к этим прямым образует с одной из них угол в 150°. Требуется найти величину отрезка секущей, расположенного между а и b.
Решение
Поскольку а II b, значит ∠MKD + ∠KDN = 180°.
Соответственно, ∠MKD = 180° — ∠KDN = 180° — 150° = 30°.
Теперь рассмотрим треугольник KDM. Мы знаем, что отрезок DM представляет собой расстояние между прямыми а и b, а значит, DM ┴ b и наш треугольник является прямоугольным.
Поскольку катет, противолежащий углу в 30°, равен ½ гипотенузы, DM = 1/2DK.
Видео:Параллельные прямые.Скачать
Углы при параллельных прямых и секущей. Вертикальные, смежные, односторонние, соответственные, накрест лежащие углы
Пусть прямая с пересекает параллельные прямые и . При этом образуется восемь углов. Углы при параллельных прямых и секущей так часто используются в задачах, что в геометрии им даны специальные названия.
Углы и — вертикальные. Очевидно, вертикальные углы равны, то есть
Конечно, углы и , и — тоже вертикальные.
Углы и — смежные, это мы уже знаем. Сумма смежных углов равна .
Углы и (а также и , и , и ) — накрест лежащие. Накрест лежащие углы равны.
Углы и — односторонние. Они лежат по одну сторону от всей «конструкции». Углы и — тоже односторонние. Сумма односторонних углов равна , то есть
Углы и (а также и , и , и ) называются соответственными.
Соответственные углы равны, то есть
Углы и (а также и , и , и ) называют накрест лежащими.
Накрест лежащие углы равны, то есть
Чтобы применять все эти факты в решении задач ЕГЭ, надо научиться видеть их на чертеже. Например, глядя на параллелограмм или трапецию, можно увидеть пару параллельных прямых и секущую, а также односторонние углы. Проведя диагональ параллелограмма, видим накрест лежащие углы. Это — один из шагов, из которых и состоит решение.
Ты нашел то, что искал? Поделись с друзьями!
1. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении , считая от вершины тупого угла. Найдите большую сторону параллелограмма, если его периметр равен .
Напомним, что биссектриса угла — это луч, выходящий из вершины угла и делящий угол пополам.
Пусть — биссектриса тупого угла . По условию, отрезки и равны и соответственно.
Рассмотрим углы и . Поскольку и параллельны, — секущая, углы и являются накрест лежащими. Мы знаем, что накрест лежащие углы равны. Значит, треугольник — равнобедренный, следовательно, .
Периметр параллелограмма — это сумма всех его сторон, то есть
2. Диагональ параллелограмма образует с двумя его сторонами углы и . Найдите больший угол параллелограмма. Ответ дайте в градусах.
Нарисуйте параллелограмм и его диагональ. Заметив на чертеже накрест лежащие углы и односторонние углы, вы легко получите ответ: .
3. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна ? Ответ дайте в градусах.
Мы знаем, что равнобедренной (или равнобокой) называется трапеция, у которой боковые стороны равны. Следовательно, равны углы при верхнем основании, а также углы при нижнем основании.
Давайте посмотрим на чертеж. По условию, , то есть .
Углы и — односторонние при параллельных прямых и секущей, следовательно,
🌟 Видео
ОДНОСТОРОННИЕ УГЛЫ, параллельные прямые, секущая. Учимся находить односторонние углы.Скачать
Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать
Параллельные прямые (задачи).Скачать
Углы при параллельных и секущей #математика #огэматематика #огэ #данирСкачать
Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать
Углы при параллельных прямых и секущей | Математика ЕГЭ 2024 #егэпрофиль #егэ #профиль #умскулСкачать
Параллельные прямые — Признак Параллельности Прямых и Свойства УгловСкачать
Геометрия 7 класс. Углы с соответственно параллельными или перпендикулярнымСкачать
ГЕОМЕТРИЯ 7 класс : Соответственные, односторонние и накрест лежащие углыСкачать
7 класс, 11 урок, Смежные и вертикальные углыСкачать
ГЕОМЕТРИЯ 7 класс. Признаки параллельности, накрест лежащие, соответственные и односторонние углыСкачать
