Пятой аксиомой Евклида была аксиома о параллельных прямых, так называемый постулат о параллельных линиях, который гласит: если две прямые образуют с третьей по одну ее сторону внутренние углы, сумма которых меньше развернутого угла, то такие прямые пересекаются при достаточном продолжении с одной стороны. То есть эта аксиома утверждает, что существует только одна прямая, проходящая через данную точку вне данной прямой и параллельной этой данной прямой.
Сложная формулировка пятого постулата Евклида о параллельных линиях породила множество гипотез и предположений о возможной зависимости его от других постулатов. Были предприняты многочисленные попытки вывести его из остальных аксиом геометрии, но, к сожалению, они оказались тщетны. Усилия доказать пятый постулат от противного также не увенчались успехом.
И все же, в начале XX века почти одновременно несколько выдающихся математиков того времени — Карл Гаусс из Германии, Я. Больяи из Венгрии и Николай Иванович Лобачевский из России пришли к мысли о существовании другой, неевклидовой геометрии, в которой верна аксиома: на плоскости через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, не пересекающие данную.
Поскольку Н. И. Лобачевский первым высказал эту идею в 1826 году, новая неевклидова геометрия была названа в его именем.
Геометрия Лобачевского имеет лишь одно отличие от евклидовой — аксиома параллельности заменяется на ее отрицание — аксиому параллельности Лобачевского.
Аксиома параллельности Лобачевского выглядит следующим образом:
Найдутся такая прямая a и такая не лежащая на ней точка A, что через A проходят по крайней мере две прямые, не пересекающие a.
Непротиворечивость аксиомы доказывается представлением модели, в которой реализуются данные аксиомы.
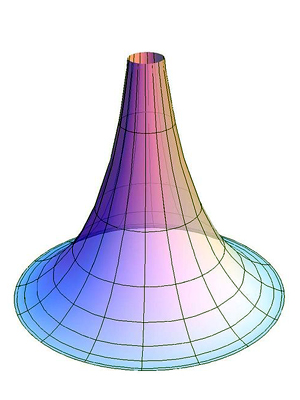
Основы аналитической геометрии, заложенные Лобачевским, практически наметили необходимую для доказательства модель. Лобачевский заметил, что орисфера в пространстве изометрична евклидовой плоскости. Полностью реализовать модель смогли работы Клейна, Пуанкаре и других ученых.
Геометрия Лобачевского нашла широчайшее применение в современной науке. Сам Николай Иванович Лобачевский использовал свою геометрию для вычисления определенных интегралов.
В теории функций комплексного переменного геометрия Лобачевского способствовала успешному построению теории автоморфных функций. В этой теории связь с геометрией Лобачевского была основой для исследований Пуанкаре. По словам Анри Пуанкаре, «неевклидова геометрия есть ключ к решению всей задачи».
Кроме того, геометрия Лобачевского стала использоваться в теории чисел, а именно, в ее геометрических методах, так называемой «геометрии чисел».
Ученые также установили тесную связь геометрии Лобачевского с кинематикой — специальной теорией относительности. В основе этой связи лежит равенство, выражающее закон распространения света:
x 2 + y 2 + z 2 = c 2 t 2 ,
при делении на t 2 , то есть для скорости света, даёт уравнение сферы в пространстве с координатами vx, vy, vz, которые являются составляющими скорости света по осям х, у, z.
Преобразование Лоренца сохраняет эту сферу, а поскольку они линейны, переводят прямые пространства скоростей в прямые. Из этого следует, (согласно модели Клейна) что в пространстве скоростей внутри сферы радиуса с , значит есть для скоростей, меньших скорости света, имеет место геометрия Лобачевского.
В общей теории относительности геометрия Лобачевского также нашла свое место. Допуская возможным тот факт, что распределение масс материи во Вселенной равномерно (это приближение в космических масштабах допустимо), то при определенных условиях пространство имеет геометрию Лобачевского. Тем самым было доказано предположение Лобачевского о новой геометрии как возможной теории пространства.
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Аксиома параллельности Лобачевского, основные следствия.
LV1. (Аксиома параллельности Лобачевского). В любой плоскости существует прямая а0 и точка А0, не принадлежащая этой прямой, такие, что через эту точку проходит по крайней мере две прямые, не пересекающие а0.
Множество точек, прямых и плоскостей, удовлетворяющих аксиомам принадлежности, порядка, конгруэнтности, непрерывности и аксиоме параллельности Лобачевского будем называть трехмерным пространством Лобачевского и обозначать через Л3. Большинство геометрических свойств фигур будут рассматриваться нами на плоскости пространства Л3, т.е. на плоскости Лобачевского. Обратим внимание на то, что формальное логическое отрицание аксиомы V1, аксиомы параллельности евклидовой геометрии, имеет именно ту формулировку, которую мы привели в качестве аксиомы LV1. На плоскости существует, по крайней мере, одна точка и одна прямая, для которых не выполнено утверждение аксиомы параллельности евклидовой геометрии. Докажем теорему, из которой следует, что утверждение аксиомы параллельности Лобачевского справедливо для любой точки и любой прямой плоскости Лобачевского.
Теорема 13.1.Пусть а – произвольная прямая, А – точка, не лежащая на этой прямой. Тогда в плоскости, определяемой точкой А и прямой а, существует по крайней мере две прямые, проходящие через А и не пересекающие прямую а.
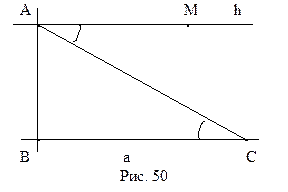
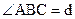
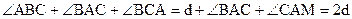
Следует заметить, что в дальнейшем мы будем пользоваться утверждением именно теоремы 13.1, по сути, заменяя им утверждение аксиомы параллельности Лобачевского. Кстати, во многих учебниках именно это утверждение принято в качестве аксиомы параллельности геометрии Лобачевского.
Из теоремы 13.1 легко получить следующее следствие.
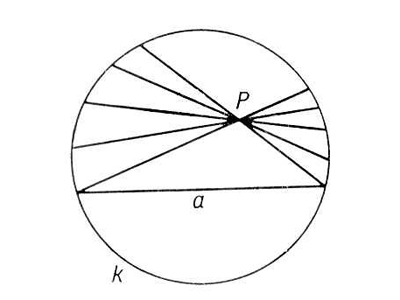
Следствие 13.2. В плоскости Лобачевского через точку, не лежащую на данной прямой, проходит бесконечно много прямых, не пересекающих данную.
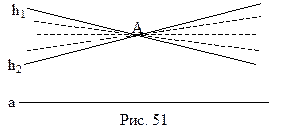
В главе 2 мы доказали ряд утверждений, эквивалентных аксиоме параллельности евклидовой геометрии. Их логические отрицания характеризуют свойства фигур на плоскости Лобачевского.
Во первых, на плоскости Лобачевского справедливо логическое отрицание пятого постулата Евклида. В параграфе 9 нами был сформулирован сам постулат и доказана теорема о его эквивалентности аксиоме параллельности евклидовой геометрии (см. теорему 9.1). Его же логическое отрицание имеет вид:
Утверждение 13.3.На плоскости Лобачевского существуют две непересекающиеся прямые, которые при пересечении с третьей прямой образуют внутренние односторонние углы, сумма которых меньше двух прямых углов.
В § 12 нами было сформулировано предложение Посидония: на плоскости существуют по крайней мере три коллинеарные точки, расположенные в одной полуплоскости от данной прямой и равноудаленные от нее. Также мы доказали теорему 12.6: предложение Посидония эквивалентно утверждению аксиомы параллельности евклидовой геометрии. Таким образом, на плоскости Лобачевского действует отрицание этого утверждения.
Утверждение 13.4. Множество точек, равноудаленных от прямой на плоскости Лобачевского и расположенных в одной полуплоскости относительно ее, в свою очередь не лежат на одной прямой.
На плоскости Лобачевского множество точек, равноудаленных от прямой и принадлежащей одной полуплоскости относительно этой прямой, образуют кривую линию, так называемую эквидистанту. Ее свойства будут рассмотрены нами позже.
Рассмотрим теперь предложение Лежандра: перпендикуляр, проведенный к стороне острого угла в любой точке этой стороны, пересекает вторую сторону угла. Доказанная нами теорема 11.6 (см. § 11) утверждает, что предложение Лежандра эквивалентно аксиоме параллельности евклидовой геометрии. Отсюда следует, на плоскости Лобачевского справедливо логическое отрицание этого предложения.
Утверждение 13.5. На стороне любого острого угла существует такая точка, что перпендикуляр к ней, восставленный в этой точке, не пересекает вторую сторону угла.
Отметим свойства треугольников и четырехугольников плоскости Лобачевского, которые непосредственно следуют из результатов параграфов 9 и 11. Прежде всего, теорема 11.1. утверждает, что предположение о существовании треугольника, сумма углов которого совпадает с суммой двух прямых углов, равносильно аксиоме параллельности евклидовой плоскости. Отсюда и из первой теоремы Лежандра (см. теорему 10.1, § 10) следует следующее утверждение
Утверждение 13.6. На плоскости Лобачевского сумма углов любого треугольника меньше 2d.
Отсюда непосредственно вытекает, что сумма углов любого выпуклого четырехугольника меньше 4d, а сумма углов любого выпуклого n – угольника меньше 2(n-1)d.
Так как на евклидовой плоскости углы, прилежащие к верхнему основанию четырехугольника Саккери равны прямым углам, что в соответствии с теоремой 12.3 (см. § 12) равносильно аксиоме параллельности евклидовой геометрии, то можно сделать следующий вывод.
Утверждение 13.7. Углы, прилегающие к верхнему основанию четырехугольника Саккери – острые.
Нам осталось рассмотреть еще два свойства треугольников на плоскости Лобачевского. Первое из них связано с предложением Валлиса: на плоскости существует хотя бы одна пара треугольников с соответственно равными углами, но не равными сторонами. В параграфе 11 мы доказали, что это предложение эквивалентно аксиоме параллельности евклидовой геометрии (см. теорему 11.5). Логическое отрицание этого утверждения приводит нас к следующему выводу: на плоскости Лобачевского не существует треугольников с равными углами, но не равными сторонами. Таким образом, справедливо следующее предложение.
Утверждение 13.8. (четвертый признак равенства треугольников на плоскости Лобачевского).Любые два треугольника на плоскости Лобачевского, имеющие соответственно равные углы, равны между собой.
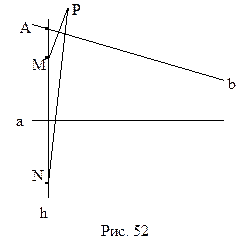
Утверждение 13.9. На плоскости Лобачевского существует треугольник, вокруг которого нельзя описать окружность.
Легко построить пример такого треугольника. Выберем некоторую прямую а и точку А, которая ей не принадлежит. Опустим из точки А перпендикуляр h на прямую а. В силу аксиомы параллельности Лобачевского существует прямая b, проходящая через А и не перпендикулярная h, которая не пересекает а (рис. 52). Как известно, если вокруг треугольника описана окружность, то ее центр лежит в точке пересечения серединных перпендикуляров сторон треугольника. Поэтому нам достаточно привести пример такого треугольника, серединные перпендикуляры которого не пересекаются. Выберем точку М на прямой h, так как показано на рисунке 52. Симметрично отобразим ее относительно прямых а и b, получим точки N и P. Так как прямая b не перпендикулярна h, то точка Р не принадлежит h. Поэтому точки M, N и P составляют вершины треугольника. Прямые а и b служат по построению его серединными перпендикулярами. Они же, как было сказано выше, не пересекаются. Треугольник MNP – искомый.
Легко построить пример треугольника плоскости Лобачевского, вокруг которого можно описать окружность. Для этого достаточно взять две пересекающиеся прямые, выбрать точку, которая им не принадлежит, и отразить ее относительно этих прямых. Проведите подробное построение самостоятельно.
Определение 14.1. Пусть даны две направленные прямые 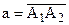
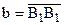
1. 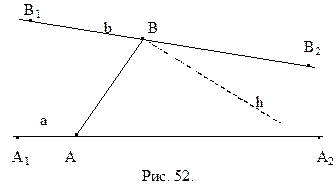
2. для произвольных точек А и В прямых а и b любой внутренний луч h угла АВB2 пересекает прямую а (рис. 52).
Обозначать параллельные прямые будем так же, как принято в школьном курсе геометрии: a || b. Заметим, что этому определению удовлетворяют параллельные прямые на евклидовой плоскости.
Теорема 14.3. Пусть на плоскости Лобачевского дана направленная прямая 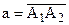
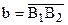
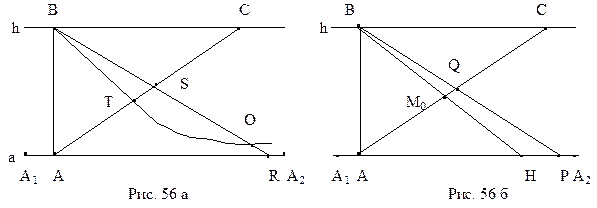
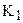
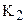
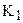
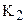
1. 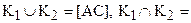
2. 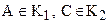
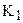
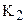
3. любая точка класса 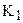
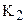
Первое условие очевидно, все точки отрезка принадлежат одному или другому классу, при этом сами классы, исходя из их определения, не имеют общих точек.
Второе условие также легко проверить. Очевидно, что 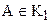
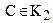
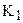
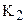
Докажем третье условие. Пусть существует такая точка S первого класса, отличная от А, и такая точка Т второго класса, что точка Т лежит между А и S (см. рис 56 а). Так как 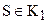
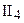
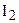
В соответствии с заключением теоремы 4.3 о дедекиндовом сечении на отрезке АС существует такая точка 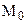
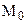
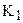
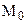
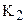
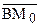
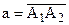
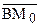
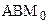

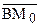
Легко проверить, что прямая 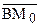

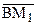
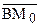

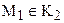
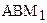

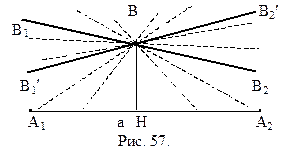
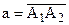
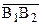
Теорема 14.4. Пусть направленная прямая 
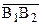
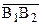

Из этой теоремы с очевидностью вытекает следующее следствие.
Следствие. Если существует общий перпендикуляр направленных прямых 
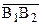

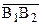
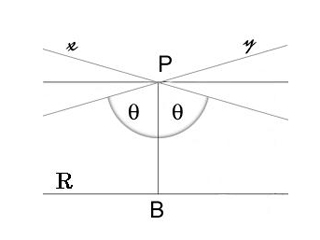
Введем понятие параллельности для ненаправленных прямых. Будем считать, что две ненаправленные прямые параллельны, если на них можно выбрать направления так, чтобы они удовлетворяли определению 14.1. Как известно, прямая имеет два направления. Поэтому, из теоремы 14.3 следует, что через точку В, не принадлежащей прямой а проходит две ненаправленные прямые, параллельные данной прямой. Очевидно, они симметричны относительно перпендикуляра, опущенного из точки В на прямую а. Эти две прямые и являются теми самыми пограничными прямыми, разделяющими пучок прямых, проходящих через точку В и пересекающих а, от пучка прямых, проходящих через В и не пересекающих прямую а (рис. 57).
Теорема 15.2. (Свойство симметричности параллельных прямых на плоскости Лобачевского).Пусть направленная прямая 
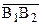
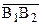

Свойство симметричности понятия параллельности прямых на плоскости Лобачевского позволяет нам не указывать порядок направленных параллельных прямых, т.е. не уточнять, какая прямая является первой, а какая второй. Очевидно, что свойство симметричности понятия параллельности прямых имеет место и на евклидовой плоскости. Оно непосредственно следует из определения параллельных прямых в евклидовой геометрии. В евклидовой геометрии выполняется также свойство транзитивности для параллельных прямых. Если прямая а параллельна прямой b, а прямая b параллельна прямой с. то прямые а и с также параллельны между собой. Аналогичное свойство справедливо и для направленных прямых на плоскости Лобачевского.
Теорема 15.3. (Свойство транзитивности параллельных прямых на плоскости Лобачевского).Пусть даны три различные направленные прямые 
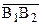
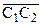
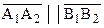
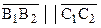
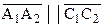
Рассмотрим направленную прямую 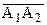
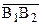
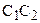
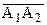
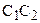
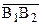
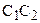
Теорема 15.4. Угол 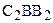
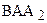
Теорема 15.5. Внешний угол вырожденного треугольника больше внутреннего угла, не смежного с ним.
Доказательство непосредственно следует из теоремы 15.4. Проведите его самостоятельно.
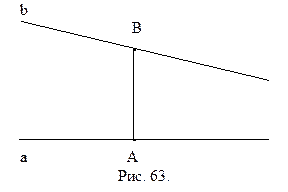
Определение 16.1. Острый угол, образованный прямыми АВ и b называется углом параллельности отрезка АВ.
Ясно, что каждому отрезку соответствует некоторый угол параллельности. Справедлива следующая теорема.
Теорема 16.2. Равным отрезкам соответствуют равные углы параллельности.
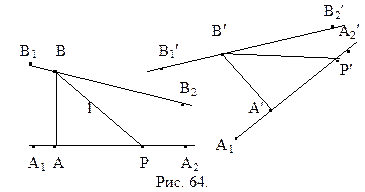
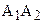
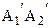
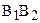
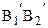
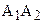
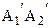
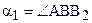
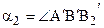
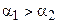
Отложим от луча ВА в полуплоскости ВАА2 угол a2, 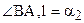
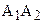
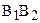
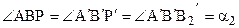
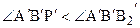
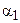
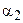
Рассмотрим теперь, как связаны между собой углы параллельности неравных отрезков.
Теорема 16.3. Пусть отрезок АВ больше отрезка А¢В¢, а углы 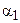
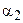
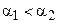
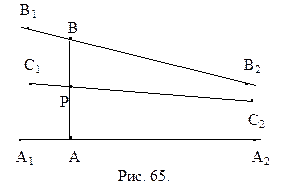
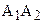
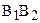
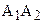
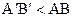
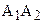
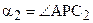
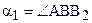
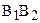
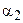
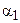
Легко доказать обратное утверждение.
Теорема 16.4.Пусть 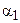
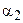
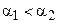
Доказательство.Предположим противное, 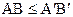
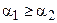
И так мы доказали, что каждому отрезку соответствует свой угол параллельности, причем большему отрезку соответствует меньший угол параллельности. Рассмотрим утверждение, в котором доказывается, что для любого острого угла существует отрезок, для которого этот угол является углом параллельности. Тем самым будет установлено взаимно однозначное соответствие между отрезками и острыми углами на плоскости Лобачевского.
Теорема 16.5. Для любого острого угла существует отрезок, для которого этот угол является углом параллельности.
Доказательство.Пусть дан острый угол АВС (рис. 66). 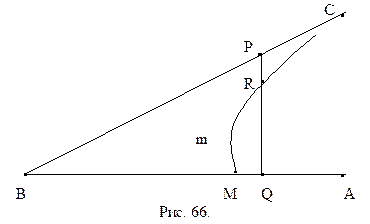
Разобьем точки отрезка ВМ на два класса. Классу 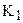
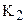
4. 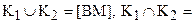
5. 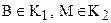
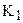
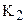
6. любая точка класса 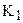
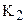
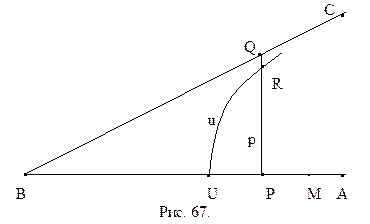
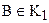
Проверим справедливость третьего условия теоремы 4.3. Предположим, что существуют такие точки 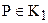
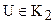
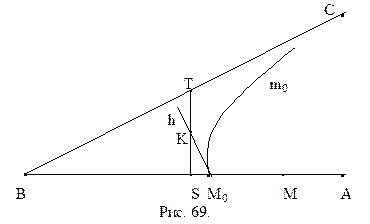
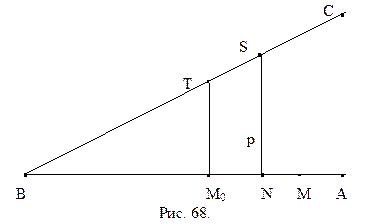
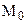
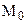
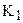
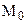
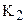
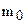
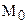
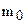
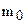
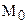
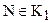
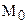
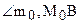
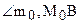
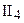
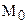
И так, мы установили, что каждому отрезку в геометрии Лобачевского можно поставить в соответствие острый угол – его угол параллельности. Будем считать, что нами введена мера углов и отрезков, отметим, что мера отрезков будет введена нами позже, в § . Ведем следующее определение.
Определение 16.6. Если под х понимается длина отрезка, а под j — величина угла, то зависимостьj = P(х), ставящая в соответствие длине отрезка величину его угла параллельности, называется функцией Лобачевского.
Ясно, что 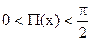
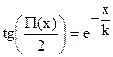
где k – некоторое положительное число. Оно имеет важное значение в геометрии пространства Лобачевского, и носит название его радиуса кривизны. Два пространства Лобачевского, имеющие один и тот же радиус кривизны, изометричны. Из приведенной формулы, как нетрудно видеть, также следует, что j = P(х) монотонно убывающая непрерывная функция, значения которой принадлежат интервалу 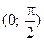
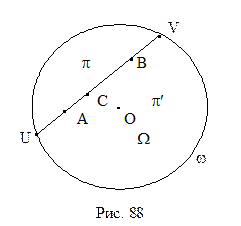
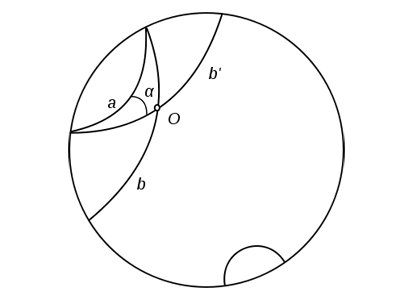
L‑плоскости имеет место аксиома параллельности Лобачевского: через L‑точку B, не лежащую на L‑прямой a проходят по крайней мере две L‑прямые b и c, не имеющие общих точек с L‑прямой a. На рисунке 94 приведена иллюстрация этого утверждения. Легко также понять, что из себя представляют параллельные направленные прямые L-плоскости. Рассмотрим рисунок 95. L-прямая b проходит через точку пересечения L-прямой a с абсолютом. Поэтому направленная L-прямая А1А2 параллельна направленной L-прямой В1А2. Действительно, эти прямые не пересекаются, и, если выбрать произвольные L-точки А и В, принадлежащие соответственно этим прямым, то любой внутренний луч h угла А2ВА пересекает прямую а. Таким образом, две L-прямые параллельны, если они имеют общую точку пересечения 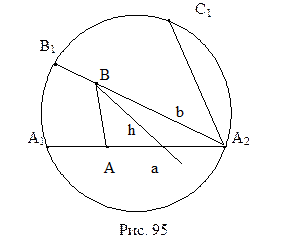
Таким образом, определенные выше основные понятия удовлетворяют требованиям аксиом I1-I3, II, III, IV групп аксиоматики Гильберта и аксиоме параллельности Лобачевского, следовательно являются моделью плоскости Лобачевского. Нами доказана содержательная непротиворечивость планиметрии Лобачевского. Сформулируем это утверждение как следующую теорему.
Теорема 1. Геометрия Лобачевского содержательно непротиворечива.
Мы построили модель плоскости Лобачевского, с построением же пространственной модели, аналогичной рассмотренной на плоскости, можно познакомиться в пособии [4].
Из теоремы 1 следует важнейший вывод. Аксиома параллельности не является следствием аксиом I – IV аксиоматики Гильберта. Так как пятый постулат Евклида равносилен аксиоме параллельности евклидовой геометрии, то этот постулат также не зависит от остальных аксиом Гильберта.
| | | следующая лекция ==> | |
| Тахеометрическая съемка | | | Параллельное проектирование и его свойства. |
Дата добавления: 2016-02-02 ; просмотров: 7114 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Геометрия 7 класс (Урок№20 - Аксиома параллельных прямых.)Скачать

ЛОБАЧЕ́ВСКОГО ГЕОМЕ́ТРИЯ
В книжной версии
Том 17. Москва, 2010, стр. 712-714
Скопировать библиографическую ссылку:
ЛОБАЧЕ́ВСКОГО ГЕОМЕ́ТРИЯ, одна из неевклидовых геометрий, основана на тех же посылках, что и обычная – евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на иную. Евклидова аксиома о параллельных состоит в том, что через точку, не лежащую на данной прямой, проходит не более чем одна прямая, лежащая с данной прямой в одной плоскости и не пересекающая её (в евклидовой геометрии такие прямые называют параллельными). В Л. г. эта аксиома заменяется следующей: через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её (достаточно, чтобы это было выполнено для одной точки и одной прямой). Начало Л. г. было положено Н. И. Лобачевским , который впервые сообщил о ней в 1826. Несколько позднее эту же теорию предложил Я. Больяй ; поэтому Л. г. иногда называют геометрией Лобачевского – Больяя. Её также называют неевклидовой геометрией, хотя обычно термину «неевклидова геометрия» придают более широкий смысл, включая сюда и др. теории, возникшие вслед за Л. г., а также теории, основанные на изменении посылок евклидовой геометрии. Л. г. иногда называют гиперболич. неевклидовой геометрией в противоположность эллиптич. геометрии Римана (см. Неевклидовы геометрии , Римана геометрия ).
🌟 Видео
1. Лобачевский и его наследие. Основные постулаты геометрии.Скачать

2. Пятый постулат геометрииСкачать

Что на самом деле доказал Лобачевский?Скачать

НЕЕВКЛИДОВАЯ ГЕОМЕТРИЯ. оказывается это так просто...Скачать

#177. ГЕОМЕТРИЯ ЛОБАЧЕВСКОГО (советский диафильм)Скачать

Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать

Геометрия 7 класс (Урок№21 - Свойства параллельных прямых.)Скачать

Мнимая ошибка, над которой ломали голову 2 000 лет [Veritasium]Скачать
![Мнимая ошибка, над которой ломали голову 2 000 лет [Veritasium]](https://i.ytimg.com/vi/yc2350IZvAk/0.jpg)
Параллельность прямых. 10 класс.Скачать

7 класс, 28 урок, Аксиома параллельных прямыхСкачать

Задачи на доказательство по геометрии. Признаки параллельности прямых.Скачать

Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

#223. МИФЫ И ЛЕГЕНДЫ школьной математикиСкачать

Лобачевский против Евклида: две геометрии одного мираСкачать

Неевклидова геометрия Лобачевского — Валентина КириченкоСкачать

7 класс, 25 урок, Признаки параллельности двух прямыхСкачать

Теорема 13.2 Если две прямые параллельны третьей, то они параллельны ||Геометрия 7 класс||Скачать

7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать