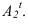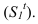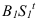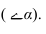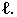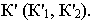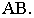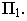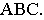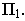Указания к лабораторным работам по
НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ (СТРОИТЕЛЬСТВО)
Тени в ортогональных проекциях.
Понятие о собственной и падающей тени (рис. 1).
Рис. 1 Собственная и падающая тень
Тень на неосвещенной части поверхности предмета называется собственной. Тень, отбрасываемая на плоскости и поверхности, называется падающей. Линия, отделяющая освещенную часть предмета от неосвещенной называется контуром собственной тени. Контур падающей тени является тенью от контура собственной тени.
Источники света.
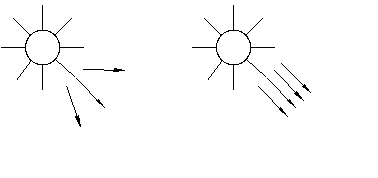
Освещение предмета называется факельным (рис. 2, а), если источник света удалён от объекта на незначительном расстояние. Когда источник света удален в бесконечность и световые лучи параллельны друг другу, освещение называется солнечным (рис. 2, б).
Рис. 2 Освещение
Чаще всего построение теней осуществляется при параллельных световых лучах.
Стандартное направление световых лучей.
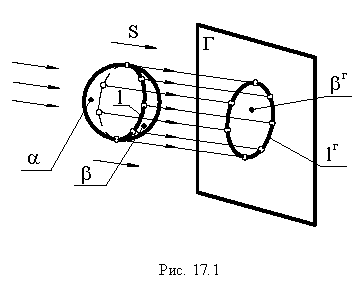
В ортогональных проекциях направление лучей принято брать по диагонали куба (рис. 3).
Рис. 3 Стандартное направление световых лучей
Такое направление лучей света удобно при построении теней, оно соответствует примерно полуденному стоянию солнца на широтах Москвы и Санкт-Петербурга летом, когда тени в натуре получаются более резкими.
Тень точки.
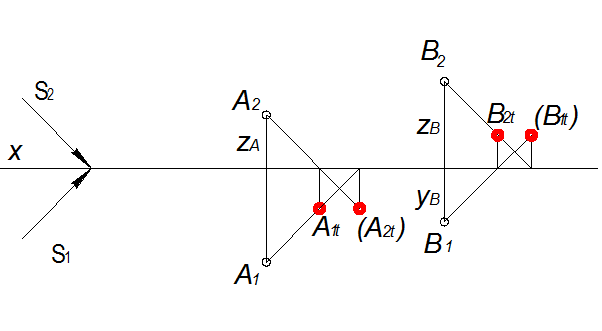
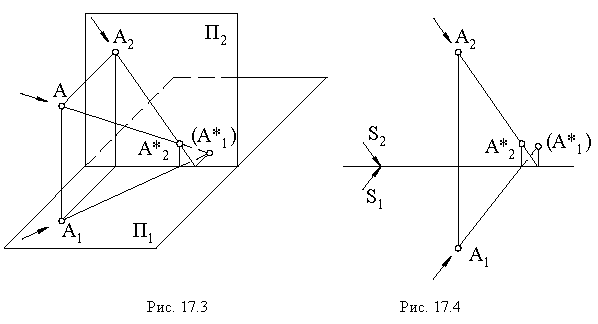
Тенью точки является след светового луча, проходящего через данную точку (рис. 4).
Рис. 4 Тень точки
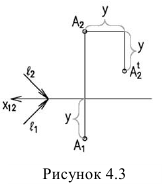
А1t – тень точки на плоскости π1.
А2t – тень точки на плоскости π2.
Если yА > zА, то реальная тень на плоскости π1.
Если zА > yА, то реальная тень на плоскости π2.
Тень точки на той плоскости проекции, которую световой луч пересекает первой называется реальной, а тень точки на плоскости, которую световой луч пересекает второй называется мнимой. Мнимую тень, если она необходима при построении, обозначают круглыми скобками.
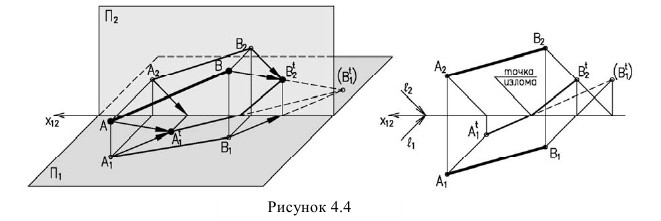
Тень от прямой общего положения (рис. 5).
Рис. 5 Тень от прямой общего положения
Если тень от прямой падает на две пересекающиеся плоскости, то на линии их пересечения тень имеет излом.
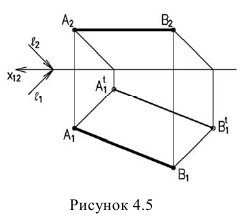
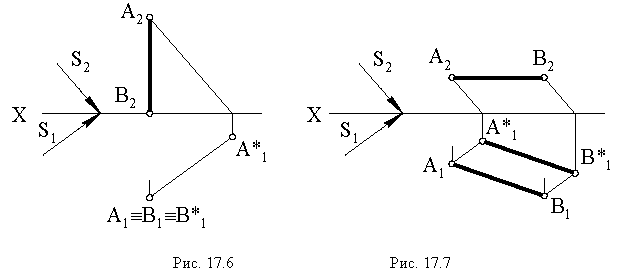
Тени от прямых частного положения (рис. 6).
Тень от прямой, перпендикулярной плоскости проекции, совпадает с проекцией светового луча на той плоскости проекции, которой прямая перпендикулярна.
Тень от прямой, параллельной плоскости проекций, параллельна проекции прямой и равна ей по величине на той плоскости проекции, которой прямая параллельна.
Рис. 6 Тени от прямых частного положения
Тени от плоских фигур.
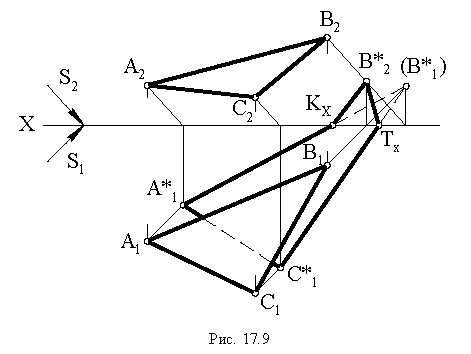
Тень от треугольника (рис. 7).
Рис. 7 Тени от треугольника
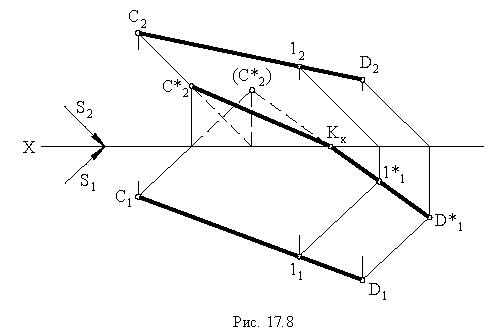
Тень от круга (рис. 8).
Рис. 8 Тени от круга
Тени в нишах (рис. 9).
Рис. 9 Тени в нишах
Тени поверхностей.
Тень от призмы (рис. 10) и от цилиндра (рис. 11).
Рис. 10 Тени от призм
Рис. 11 Тени от цилиндра
Методы построения теней.
а) Метод лучевых секущих плоскостей.
б) Метод обратного луча.
Метод лучевых секущих плоскостей.
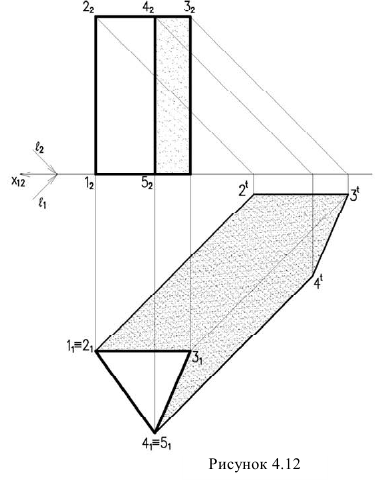
Сущность метода состоит в том, что для построения тени, падающей от одного объекта на другой, через характерные точки объекта проводится ряд лучевых секущих плоскостей, строятся по точкам вспомогательные сечения и определяются точки пересечения ряда лучевых прямых, проведенных через характерные точки первого объекта, с построенными сечениями второго. Построив ряд точек падающей тени и соединив их в определенной последовательности, получим контур падающей тени (рис. 12).
Рис. 12 Метод лучевых секущих плоскостей
Метод обратного луча.
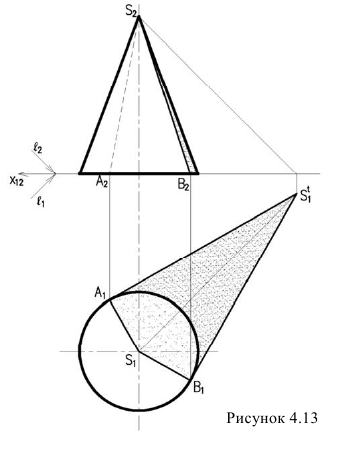
Сущность этого метода заключается в следующем (рис. 13, 14):
1) Строятся падающие тени двух предметов.
2) Определяются точки пересечения падающих теней.
3) Обратным лучем находят тень точек пересечения на исходном чертеже.
4) Найденные точки соединяются.
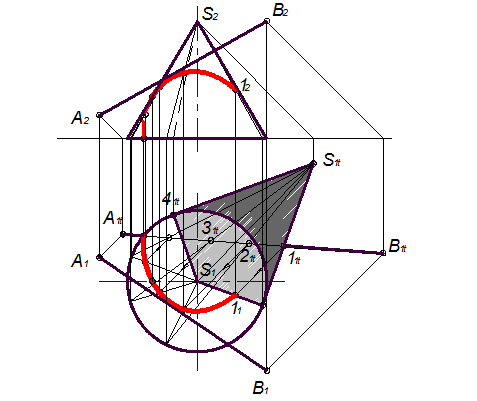
Рис. 13 Тень от прямой на треугольник
Рис. 14 Тень от прямой на конус
Перспектива.
Основные элементы перспективы. Перспектива точки.
Перспективой называется наглядное изображение предмета, построенное методом центрального проецирования.
Различают три вида перспектив:
Наглядное изображение, построенное на плоскости методом центрального проецирования, называется линейной перспективой.
Наглядное изображение, построенное на внутренней поверхности цилиндра, называется панорамной перспективой.
Наглядное изображение, построенное на внутренней поверхности сферы, называется купольной перспективой.
Перспектива точки (рис. 15).
Рис. 15 Перспектива точки
K – вертикальная плоскость проекции (картинная плоскость или картина).
K1 – основание картины.
π1 – предметная плоскость.
h – линия горизонта.
S – точка зрения.
S1 – основание точки зрения.
SP – главное расстояние картины.
P – главная точка картины.
P1 – основание главной точки картины.
А’ – перспектива точки А.
А’1 – вторичная проекция точки А.
Если точка находится в бесконечности, то ее вторичная проекция всегда лежит на линии горизонта. Если точка принадлежит картинной плоскости, то перспектива точки совпадает с самой точкой, а вторичная проекция точки всегда лежит на основании картины. Если точка принадлежит предметной плоскости, то перспектива точки и ее вторичная проекция совпадают.
Перспектива прямых общего положения (рис. 16).
Рис. 16 Перспектива прямой
N – начальная точка.
F – бесконечно удаленная (предельная) точка.
Перспектива прямых частного положения.
а) Горизонтальные прямые, точки схода которых в перспективе располагаются на линии горизонта (рис. 17).

б) Прямые, перпендикулярные картине, точкой схода которых является главная точка картины P (рис. 18).
Рис. 18 Перспектива прямой, перпендикулярной картине
в) Горизонтальные прямые, расположенные по углом 45° к картине, точками схода которых в перспективе являются дистанционные точки D1 и D2 (рис. 19).
Рис. 19 Перспектива прямой, расположенной под углом 45° к картине
г) Прямые, параллельные картине, не имеют точек схода, их перспективы параллельны самим прямым (рис. 28).
Рис. 20 Перспектива прямой, параллельной картине
Перспектива параллельных прямых.
Перспективы параллельных прямых пересекаются, т. е. имеют одну точку схода (рис. 21).
Рис. 21 Перспектива параллельных прямых
Выбор картинной плоскости и точки зрения.
При выборе точки зрения рекомендуется придерживаться следующих положений:
1) Линия горизонта выбирается в зависимости от вида перспективы:
а) H ≈ 1,7 м. Перспектива с нормальной точкой зрения (для одного здания).
б) H ≈ 100 м. Перспектива с высоким горизонтом (для группы зданий).
в) H ≈ 0 м. Перспектива снизу (для отдельных деталей, наблюдаемых снизу, и для зданий, стоящих на возвышении).
2) Картинная плоскость проводится через один из углов здания. Угол наклона картинной плоскости к фасаду – 25° – 30°.
3) Точка зрения выбирается так, чтобы было видно две стены здания.
4) Угол зрения φ = 18° – 58°.
5) Главный луч зрения должен быть направлен перпендикулярно картинной плоскости и делить картину примерно пополам или находиться в средней трети между крайними лучами, идущими от зрителя к предмету.
Способы построения перспективы.
1) Радиальный способ (способ следа луча).
2) Способ архитектора:
а) С одной точкой схода.
б) С двумя точками схода.
Радиальный способ.
Сущность радиального способа построения перспективы заключается в определении точек пересечения проецирующих лучей с картинной плоскостью, с помощью построения картинных следов прямых. Он находит применение при построении фронтальных перспектив улиц, внутренних дворов, фасадов зданий с выступающими вперед частями и т. д.
Перспектива точки, построенная радиальным методом (рис. 22).
Рис. 22 Перспектива точки А, построенная радиальным способом
Способ архитектора с двумя точками схода.
Основан на использовании двух точек схода перспектив параллельных горизонтальных прямых объекта (рис. 23).
Рис. 23 Перспектива плоской фигуры, построенная способом архитектора с двумя точками схода
Способ архитектора с одной точкой схода.
Основан на использовании одной точки схода и картинных следов прямых (рис. 24).
Рис. 24 Перспектива плоской фигуры, построенная способом архитектора с одной точкой схода
Перспектива здания с использование одной точки схода и опущенного плана (рис. 25).
- Тени в ортогональных проекциях в начертательной геометрии с примерами
- Тень точки — способ следа луча, способ выноса
- Тень примой общего положении
- Тени прямых частного положении
- Тени плоских фигур
- Тень окружности
- Тени поверхностей. Понятие собственной и падающей тени
- Тени в ортогональных проекциях. Метод лучевых сечений, метод обратных лучей. Тени фрагментов зданий
- Тень точки на плоскость общего положения. Способ лучевых сечений
- Способ обратного луча
- Тени схематизированною здании, состоящею из призматических форм
- Тени фрагментов зданий
- Тени в нишах
- Тень падающая от трубы на крышу
- Тень от барьера на ступенях лестницы
- Тени в ортогональных проекциях
- Тень от точки на плоскость проекций
- Тень от точки на плоскую фигуру
- Тень от прямой линии
- Тени на плоскости проекций от прямые частного положения
- Тени на плоскости проекций от прямых общего положения
- Тень от прямой на произвольную плоскость
- Тень от плоской фигуры
- Метод обратных лучей
- Тени геометрических тел
- Тени призмы
- Тени пирамиды
- Тени цилиндра
- Тени конуса
- Тени элементов зданий
- Тени в перспективе
- Падающие тени от точки, прямой и плоской фигуры. Способ следа луча.
- 🎬 Видео
Видео:Построение параллельной плоскости на расстояние 30 мм.Скачать

Тени в ортогональных проекциях в начертательной геометрии с примерами
Содержание:
Проекционные чертежи архитектурных объектов выполненные в одних линиях, не дают достаточно полного представления о запроектированном объекте.
Для придания объемности и наглядности ортогональным чертежам зданий и сооружений выполняется построение теней.
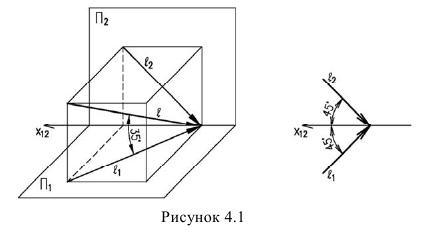
Тени строятся от естественного освещения, т.е. солнца. Так как солнце практически бесконечно удаленная точка, то лучи принимаются параллельными. За направление лучей принимается диагональ куба грани которого совпадают с плоскостями проекций, а её проекции являются диагоналями граней куба, т.е. квадратов (см. рисунок 4.1). Истинный угол наклона будет равен 35°, а проекции лучей располагаются под углом 45° к оси (см. рисунок 4.1).
Видео:10 класс, 18 урок, Теорема о прямой, перпендикулярной к плоскостиСкачать

Тень точки — способ следа луча, способ выноса
Тенью точки на плоскости является точка пересечения светового луча, проведенного через данную точку, с плоскостью. Если тень точки падает на плоскость проекций, то для её построения используется способ следа луча. Т.е. через проекции точки проводим проекции лучей и строим след. На рисунке 4.2 след луча фронтальный, следовательно тень падает на фронтальную плоскость —
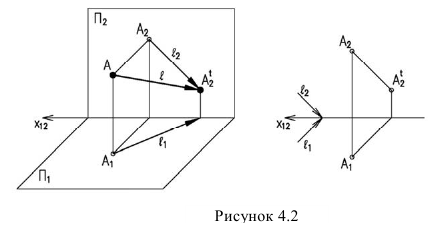
Кроме этого может быть использован метод выноса. Особенно важен этот метод при построении теней на фасадах зданий.
Вынос — это расстояние от точки до фронтальной плоскости или плоскости фасада, если тень строится на фасаде. На рисунке 4.3 у — эго вынос.
Тень примой общего положении
Тенью прямой на плоскость является линия пересечения лучевой плоскости, проведенной через прямую с заданной плоскостью. Т.е. тенью прямой на плоскость является прямая линия. Поэтому для построения тени прямой на плоскость, достаточно построить тени двух ее точек.
Если же тень от прямой падает на две плоскости, то она имеет точку излома, лежащую на линии пересечения плоскостей. В данном случае точка излома лежит на оси (рисунок 4.4). Для ее нахождения, необходимо строить мнимую тень 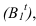
Тени прямых частного положении
Тени прямых частного положения на плоскостях проекций располагаются всегда определенно и часто служат «опорными» при построении теней различных деталей, включающих такие прямые. Рассмотрим эти случаи.
Тень от прямой, на плоскость ей параллельную, располагается параллельно прямой, т.е. параллельно проекции прямой на эту плоскость и равна ей по величине (рисунок 4.5).
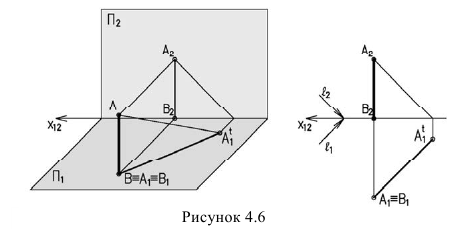
Тень от прямой на плоскость, ей перпендикулярную, располагается по проекции луча, т.е. под углом 45° (рисунок 4.6).
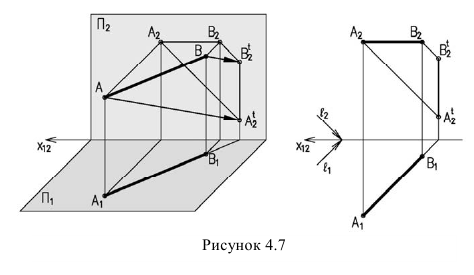
Если точка лежит на плоскости, то тень совпадает с самой точкой и такая точка называется сама себе тень. В нашем случае это точка В. Тень на фронтальной плоскости от горизонтальной прямой, расположенной под углом 45° к ней, вертикальна (рисунок 4.7)
Тени плоских фигур
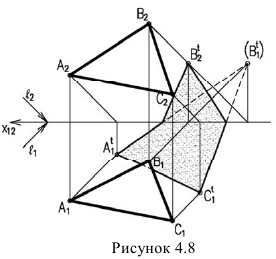
Чтобы построить тень от плоской фигуры, например треугольника, падающую на плоскости проекций достаточно построить тени от вершин (рисунок 4.8). Т.к. тень падает на две плоскости необходимо определять линию излома тени, а, следовательно, построить мнимую тень от вершины В.
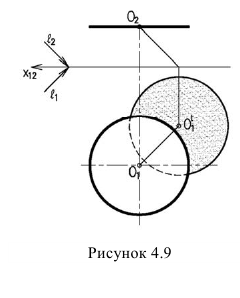
Тень от плоской фигуры, на плоскость ей параллельную, изображается фигурой равной ей по величине. Поэтому достаточно построить тень от одной точки и вычертить тень в виде той же фигуры. Так, для построения тени от окружности (рисунок 4.9) достаточно определить тень от центра и вычертить тень в виде такой же окружности.
Тень окружности
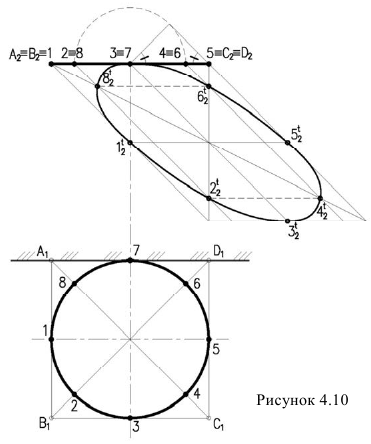
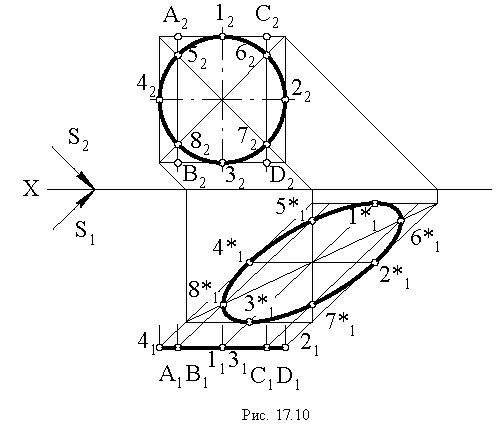
Тень окружности обычно строится по восьми точкам. Из них четыре -точки касания окружности к сторонам описанного около окружности квадрата, и четыре — точки пересечения окружности с диагоналями этого квадрата (рисунок 4.10).
Тень от квадрата — параллелограмм, диагональ которого BD вертикальна. Точки 1,3,5,7 точки касания к параллелограмму. Точки, лежащие на диагоналях, делят радиус в отношении 0,707. Они могут быть получены без горизонтальной проекции. Для этого на
радиусе строим равнобедренный треугольник с углами при основании 45° и дугой окружности определяем положение точек 2,8 и 4,6. Проведем из них лучи до пересечения с диагоналями. Полученные восемь точек соединяем плавной линией, которая будет эллипсом. Практически тень окружности по восьми точкам строят без горизонтальной проекции, которая здесь приведена только для пояснения.
Тени поверхностей. Понятие собственной и падающей тени
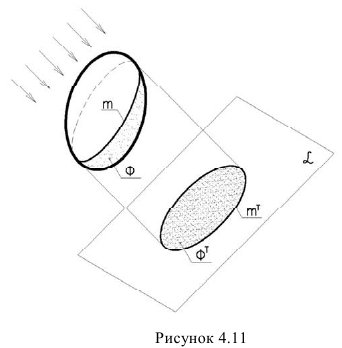
Для поверхностей характерны следующие понятия: Собственная тень (ф) — неосвещенна часть поверхности (предмета) рисунок 4.11.
Контур собственной тени (ш)-граница между освещенной и неосвещенной частью поверхности (предмета).
Падающая тень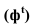
Контур падающей тени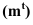
Фактически контур падающей тени -это тень от контура собственной тени. Поэтому, обычно, сначала определяют контур собственной тени, а затем уже строят падающую.
Рассмотрим примеры построения теней трехгранной призмы (рисунок 4.12) и прямого кругового конуса (рисунок 4.13).
Проведя лучи на горизонтальной проекции касательные к крайним ребрам призмы, определяем контур собственной тени. Она является пространственной ломаной 1,2,3,4,5. Т.к. точки 1 и 5 лежат на плоскости 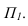
Поэтому для построения контура падающей тени, достаточно построить тени точек 2,3,4.
Проанализировав построенную тень, мы видим, что тени от ребер 1,2 и 5,4 совпадают с направлением лучей, т.к. они перпендикулярны к плоскости 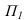
Учитывая это, построение контуров падающих теней многогранников может быть значительно упрощено.
Для конуса логично сначала построить падающую тень, а затем собственную (рисунок 4.13). Для построения падающей тени, строим тень от вершины конуса
Из полученной точки проводим касательные к окружности основания. Эти касательные образуют, контур падающей тени (она является тенями от образующих конуса). Поэтому, соединив точки А и В с вершиной конуса S получим границы собственной тени конуса. А затем уже строим фронтальную проекцию контура собственной тени. Аналогично строятся тени пирамидальных поверхностей.
Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Тени в ортогональных проекциях. Метод лучевых сечений, метод обратных лучей. Тени фрагментов зданий
Тень точки и прямой на плоскость общего положения (способ лучевых сечений, способ обратных лучей).
Тени схематизированного здания, состоящего из призматических форм.
Тени фрагментов зданий.
Тень точки на плоскость общего положения. Способ лучевых сечений
Для построения тени точки М на плоскость 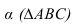
Через луч проводим горизонтально-проецирующую лучевую плоскость о. Строим линию пересечения 1-2 плоскости а и заданной плоскости 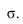
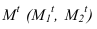
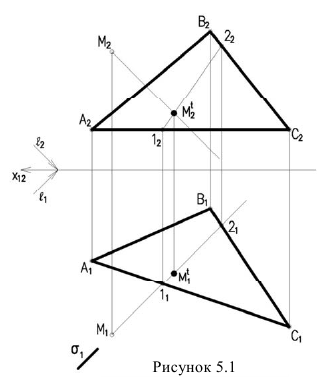
Способ обратного луча
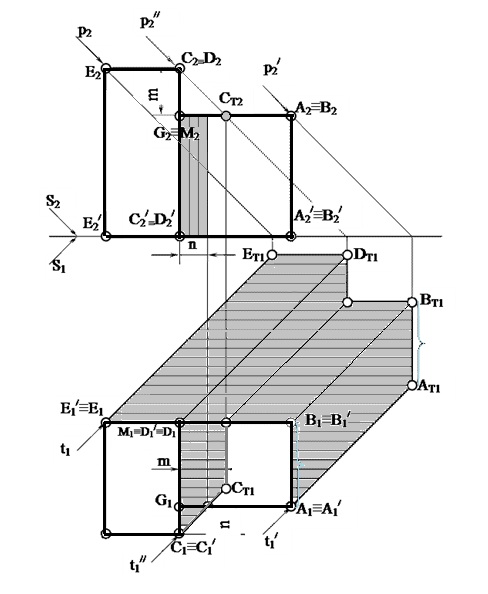
Рассмотрим построение тени от двух прямых SF и SB на непрозрачную пластинку ECDF. (рисунок 5.2).
Тень от проецирующей прямой SA строится, аналогично предыдущему примеру (рисунок 5.1), методом лучевых сечений. На горизонтальной проекции тень совпадает с направлением луча, на фронтальной — идет по лучевому сечению. Тень от точки S на пластину ESDF не надает. Для построения тени от наклонной прямой SB на пластину ESDF, необходимо построить сначала тень падающую на плоскость 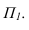
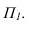
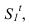
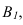
Далее строим тень от пластины ESDF на плоскость 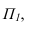
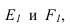
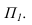
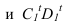
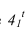
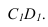
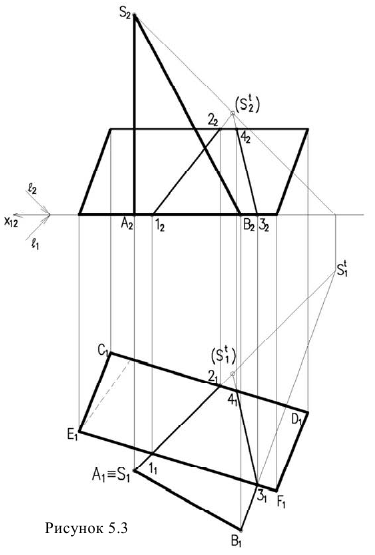
Необходимо отметить что данную задачу можно решить используя построение мнимой тени от точки S на пластину ESDF (рисунок 5.3).
Тени схематизированною здании, состоящею из призматических форм
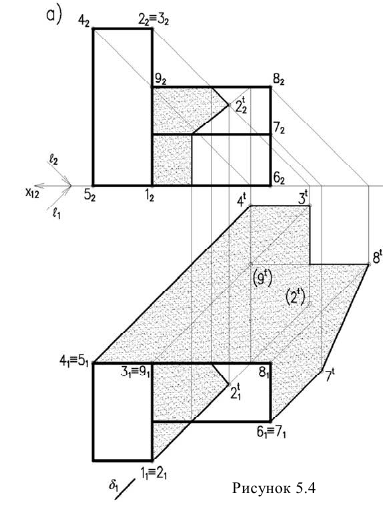
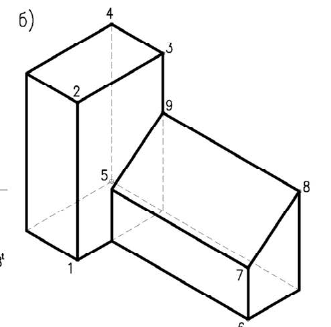
Здание состоит из двух призматических форм (рисунок 5.4). Обычно сначала строятся тени от двух этих форм падающие на плоскость 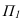
Дли построении падающих теней определяем контур собственной тени каждой из призм (рисунок 5.46). Высотная часть здания представляет прямую призму, контур собственной тени которой 1,2,3,4,5, причем точки 1 и 5 лежат на плоскости, поэтому тени строим от трех точек 2,3,4. Контур собственной тени второй призмы — 6,7,8,9. Точка 6 лежит на 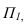
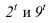
Для построения тени падающей от высотной части здания на пристройку используем метод лучевых сечений. Заключаем луч, проведенный через точку 2 в плоскость 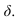
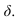
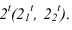
При построении теней зданий очень важно помнить положение теней прямых частного положения, это значительно упрощает процесс построения.
Тени фрагментов зданий
К фрагментам зданий относятся ниши, козырьки, трубы, лестницы и т.п. Рассмотрим построение теней некоторых из них.
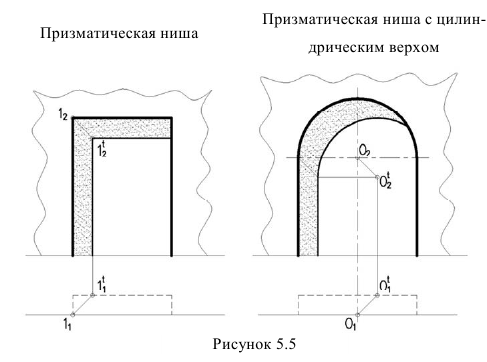
Тени в нишах
Две изображенные ниши относятся к нишам с плоским днищем, т.е. контур ниши отбрасывает тень на плоскость днища ниши параллельной контуру. Поэтому тени в нишах с — плоским днищем повторяют контур ниши. Для построения таких теней достаточно построить тень одной точки, как показано на примере (рисунок 5.5). Если дан лишь фасад здания, необходимо знать глубину ниши и тень построить методом выноса.
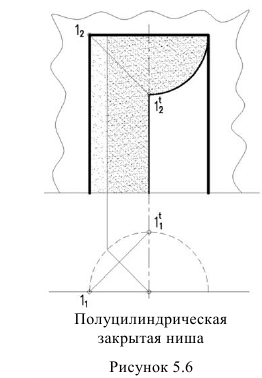
В цилиндрической нише (рисунок 5.6) сначала определяем собственную тень. Для чего удобнее провести нормаль (т.е. радиус под углом 45°). Получим контурную образующую собственной тени.
Падающую тень будет отбрасывать две прямые кромки ниши — вертикальная и продольная. Тень от вертикальной прямой надает на ось ниши. Тень от продольной прямой будет представлять четверть окружности.
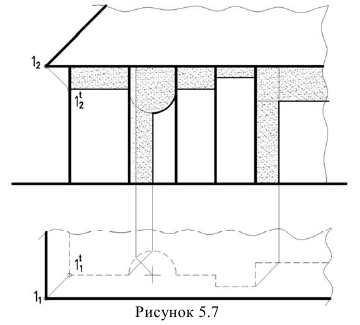
Из этого чертежа можно сделать вывод: тень от продольной прямой на фасаде с вертикальными образующими зеркально повторяется план. Этот вывод позволяет построить тень на фасаде от свеса крыши, построив тень одной точки (тень точки 1 на рисунке 5.7). Остальной контур тени зеркально повторяет план.
Тень падающая от трубы на крышу
На рисунке 5.8 дана труба призматической формы.
Тень строится методом лучевых сечений. Если отсутствует план здания, то нужно иметь ввиду, что тени от вертикальных прямых на фасаде имеют угол наклона равный углу наклона ската крыши
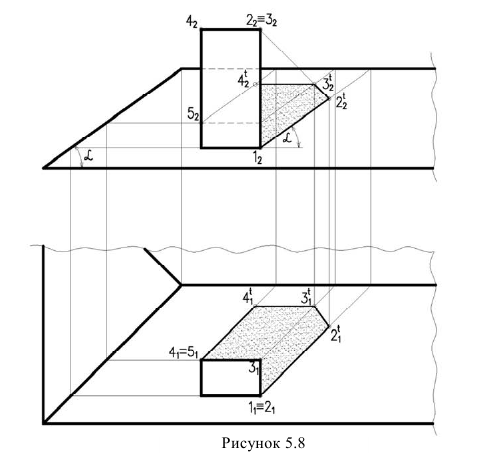
Тень от барьера на ступенях лестницы
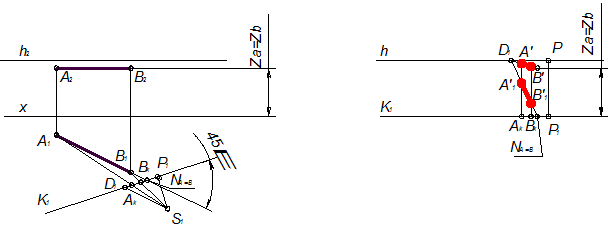
Контур собственной тени барьера (рисунок 5.9), отбрасывающий тень на ступени представляет собой две прямые — горизонтально-проецирующую 1,2 и фронтально-проецирующую 2,3. Из точек 1 и 3 начинается тень. Следовательно, необходимо построить тень точки 2. Для построения падающей тени используется метод лучевых секущих плоскостей.
Видео:Взаимно перпендикулярные плоскости. Определение кратчайшей расстоянии от точки до прямойСкачать

Тени в ортогональных проекциях
Строительство зданий и сооружений ведется по чертежам, выполненным в ортогональных проекциях. Представление о внешнем виде здания, в основном, создается по изображению фасада. Это изображение имеет существенный недостаток — в нем отсутствует объемность. Тени, построенные на ортогональных чертежах, дают возможность представить по чертежу расположение отдельных элементов, их освещенность, а также помогают находить наилучшие пропорции проектируемых зданий и сооружений.
При освещении лучами света каких-либо объектов на них образуются тени. Для образования тени необходим источник света и плоскость, на которую падает тень.
Освещение может быть центральным (факельным) или параллельным (солнечным). Освещение называется центральным в случае, когда световые лучи идут из одной точки (лампа, свеча); параллельным, если источник света (солнце) удален в бесконечность, и световые лучи практически будут параллельны между собой.
Основной геометрической задачей построения теней является определение контуров собственных и падающих теней (рис. 17.1).
Неосвещенная часть поверхности тела 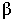
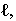
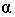
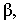
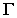
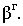
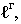
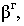
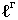
Для построения падающей тени необходимо знать направление лучей света. Направление световых лучей 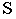
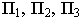
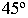
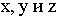
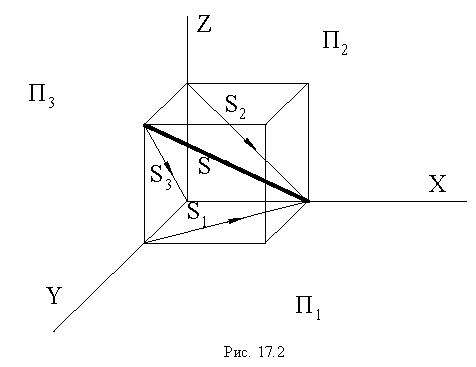
Тень от точки на плоскость проекций
Тенью от точки 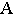
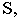
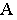
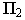
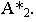
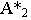
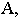
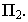
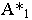
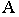
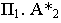
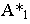
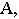
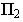
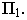
Тень от точки на плоскую фигуру
Чтобы построить тень от точки на плоскость общего положения (рис. 17.5), необходимо найти точку пересечения луча света, проходящего через заданную точку 
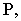
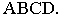
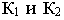
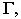
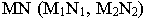
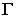
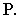
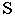
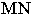
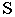
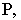
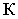
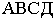
Тень от прямой линии
Построение тени от отрезка прямой линии сводится к определению тени двух или нескольких его точек. Тень от прямой можно рассматривать как след лучевой плоскости, проходящей через данную прямую. В зависимости от положения прямой, лучевая плоскость может быть общего и частного положения. Линия пересечения её с плоскостями или поверхностями определит форму тени от отрезка прямой.
Тени на плоскости проекций от прямые частного положения
Построение тени от отрезка прямой 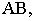
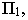
Тень 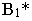
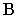
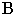
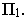
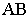
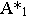
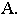
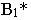
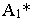
Вывод. Тень от прямой, перпендикулярной плоскости проекций, совпадает с проекцией светового луча на эту плоскость.
На рис. 17.7 показано построение тени от отрезка прямой 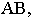
Вывод. Тень от отрезка прямой, параллельной плоскости проекций, на этой плоскости равна и параллельна самому отрезку.
Тени на плоскости проекций от прямых общего положения
На рис. 17.8 показано построение тени от отрезка прямой 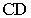
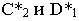
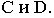
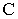
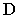
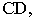
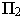
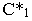
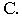
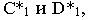
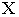
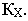
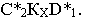
Тень от прямой на произвольную плоскость
Для построения тени от прямой на плоскость общего положения достаточно определить тени на эту плоскость от двух любых точек прямой (см. построение тени от точки на плоскую фигуру, рис. 17.5).
Тень от плоской фигуры
Падающая тень от плоской фигуры на плоскости проекций может быть построена как совокупность теней от её вершин и сторон. Таким образом, построение тени от плоской фигуры на плоскость проекций может быть сведено к известному определению теней от точек и прямых.
На рис. 17.9 показано построение тени от треугольника 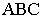
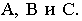
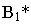
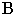
На рис. 17.10 построена тень от круглой пластины, перпендикулярной плоскости проекций 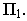
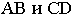
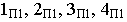
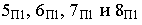
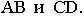
Соединив полученные точки, получим контур падающей тени круглой пластины, перпендикулярной плоскости
Метод обратных лучей
Метод обратных лучей применяется при построении теней, падающих от одного предмета на другой. Суть метода заключается в том, что строят тени заданных геометрических фигур на одну из плоскостей проекций и определяют точки пересечения теней. Через отмеченные точки проводят луч, направление которого противоположно световым лучам. Каждый из обратных лучей, пересекая данные геометрические фигуры, определяет нужные для построения тени точки.
На рис. 17.11 показано применение этого метода на примере построения тени прямой на плоскость треугольника. Построены падающие тени треугольника 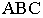
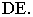
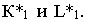
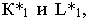
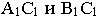
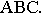
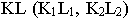
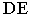
Вывод. Если падающие тени двух геометрических образов пересекаются, то тень от одного из них будет падать на другой
Тени геометрических тел
При построении теней геометрических тел вначале определяют контур собственной тени, затем находят контур падающей тени путем построения падающих теней от вершин и сторон ломаной линии (или точек кривой линии), являющейся контуром собственной падающей тени
В отдельных случаях бывает целесообразно определять контур собственной тени по уже построенной падающей тени.
Рассмотрим процесс построения теней от основных геометрических тел.
Тени призмы
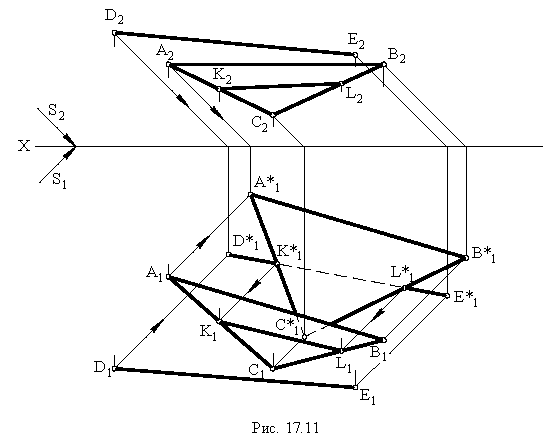
Контур тени от призмы определяется тенями от рёбер (рис. 18.1). Освещенность призмы легко определить по горизонтальной проекции, где видно, что обращенными к свету являются две грани 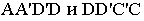
Тени пирамиды
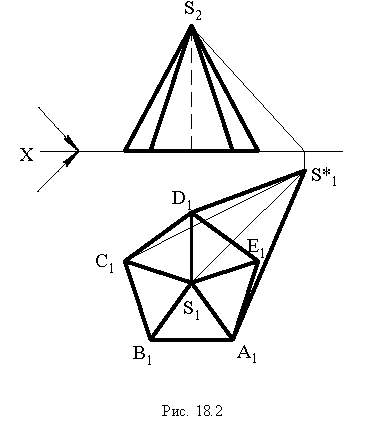
Построим тени пятиугольной пирамиды (рис. 18.2). Строим падающую тень 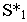
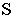
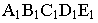
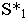
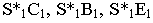
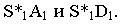
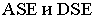
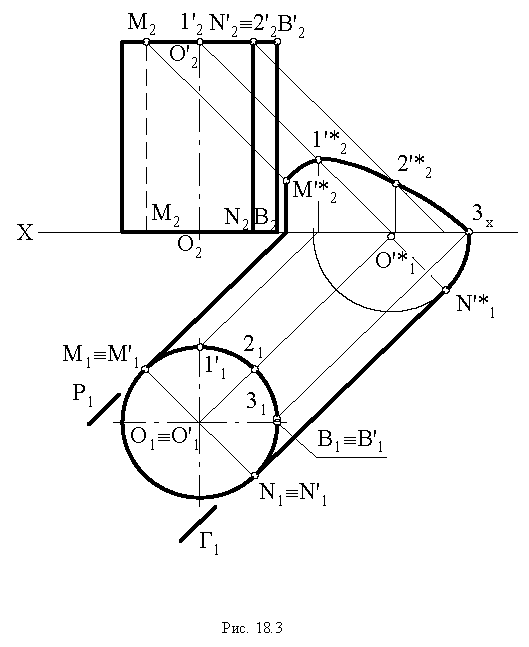
Тени цилиндра
Для определения контура собственной тени прямого кругового цилиндра необходимо провести две горизонтально-проецирующие лучевые плоскости 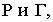
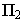
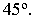
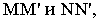
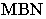
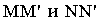
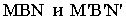
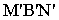
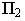
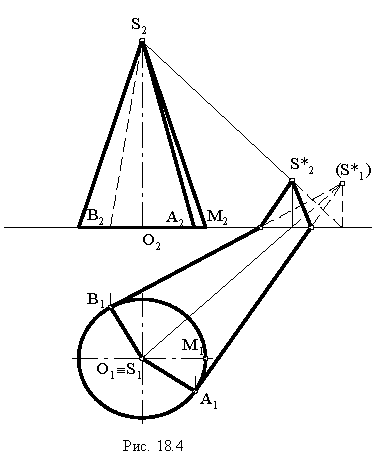
Тени конуса
На рнс. 18.4 показано построение собственной и падающей теней прямого кругового конуса. Вначале определяем мнимую тень от вершины конуса 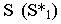
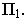
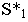
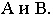
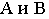
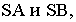
Тени элементов зданий
При построении проекций теней на фасадах зданий используются те же приемы, что и при построении теней геометрических тел.
Рассмотрим примеры построения теней некоторых частей здания
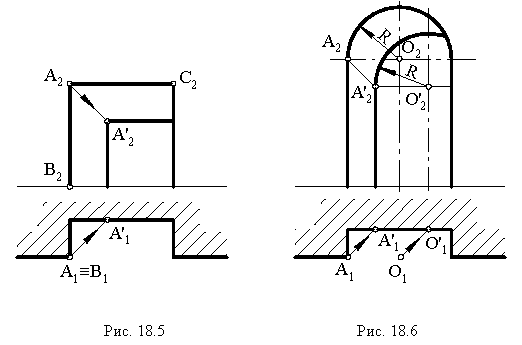
На рис. 18.5 показан пример построения теней в плоской нише. Определение границы падающей тени заключается в построении тени от ломаной линии 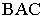
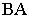
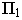
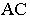
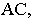
На рис. 18.6 приведен пример построения тени в прямоугольной нише с цилиндрической аркой В этом примере надо найти тень от точки 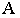
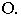
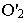
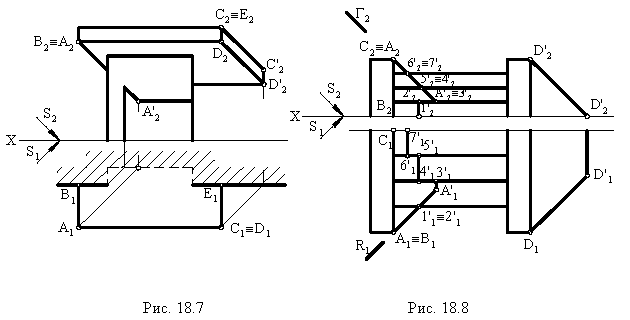
На рис. 18.7 построена тень от козырька (или балкона) здания Построения понятны из чертежа.
На рис. 18.8 показано построение теней на лестнице (крыльце). В собственной тени находятся правые грани вертикальных стенок. Падающая тень от правой стенки лестницы на плоскость стены здания и на землю строится как тень от плоской фигуры на плоскости проекций 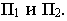
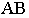
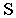
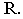
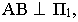
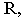
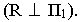
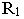
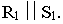
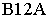
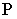
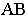
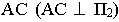
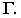
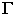
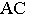
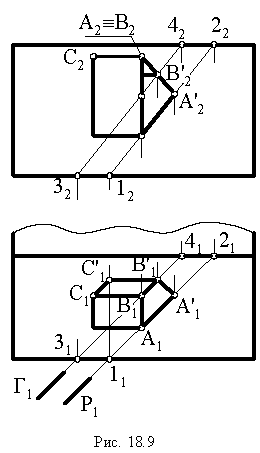
На рис. 1S.9 показано построение контура падающей тени от трубы на скат крыши здания Задача сводится к определению теней от точек и прямых на произвольно расположенную плоскость (скат крыши). Построения выполнены способом вспомогательных секущих лучевых плоскостей 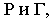
Тени в перспективе
При построении теней в перспективе в качестве источника света рассматривается естественный источник — солнце. Правила построения теней в перспективе точно такие же, как и в ортогональных проекциях.
Для упрощения построения считают, что световые лучи параллельны плоскости картины, тогда на картине перспективы оснований лучей будут параллельны основанию картины
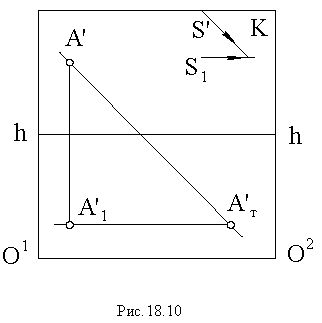
Если на картине задана перспектива 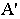
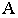
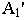
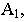
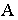
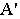
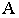
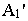
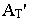
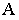
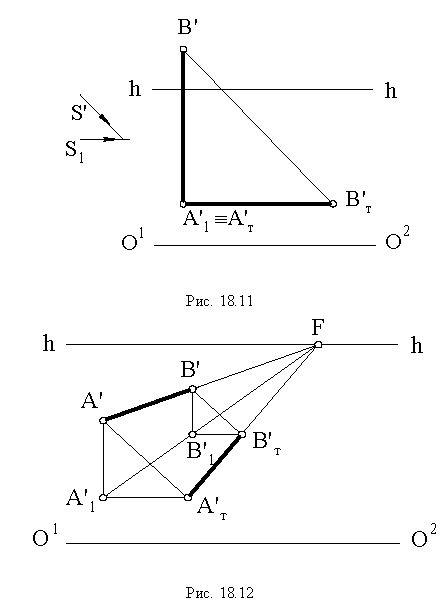
Построение тени от прямой сводится к построению тени от двух ее точек. При этом, если прямая перпендикулярна предметной плоскости (рис. 18.11), то тень от нее на этой плоскости совпадает с основанием луча, проведенного через основание прямой.
Тень от вертикальной прямой на вертикальной плоскости вертикальна.
Если прямая параллельна предметной плоскости (горизонтальная прямая), то тень от нее на этой плоскости будет параллельна данной прямой (рис. 18.12) и направлена в точку схода.
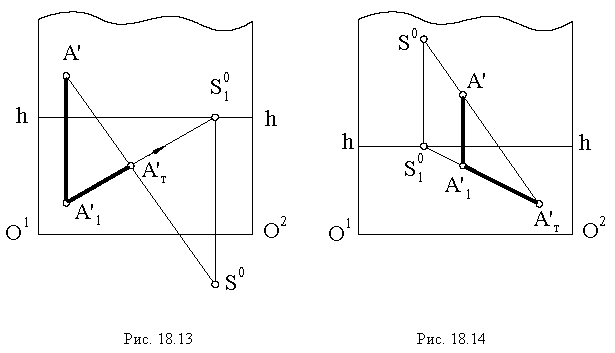
Тени в перспективе могут быть построены с различных точек расположения источника света. Направление лучей света может быть выбрано в зависимости от характера объекта и от желания показать его освещенным с той или другой стороны. Так, например, если источник света будет находиться позади предмета (рис. 18.13) или перед зрителем, но позади предмета (рис. 18.14), то для построения перспективы тени 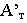
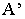
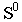
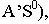
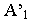
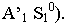
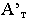
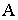
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Кривые поверхности
- Пересечения криволинейных поверхностей
- Пересечения поверхностей с прямой и плоскостью
- Взаимное пересечение поверхностей
- Развертки поверхностей
- Способы преобразования проекций
- Взаимное положение прямой и плоскости
- Решение метрических задач
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:10 класс, 6 урок, Параллельность прямой и плоскостиСкачать

Падающие тени от точки, прямой и плоской фигуры. Способ следа луча.
ТЕНИ В ОРТОГОНАЛЬНЫХ ПРОЕКЦИЯХ

Падающие тени от точки, прямой и плоской фигуры. Способ следа луча.

Тень от точки на какую-либо поверхность (см. рис. 2) является точкой пересечения с этой поверхностью луча света, проведённого через данную точку. От точки, расположенной в пространстве тень может падать или на пл. π1 или π2 . На рис.2 показано построение тени точек А и В на эпюре. Из двух теней Ат и А т у, Вт и В т у, первые — Ат и Вт будут реальными и действительными, вторые — А т у и В т у будут мнимыми.
Тень от прямой линии на поверхность — это есть линия пересечения лучевой плоскости с этой поверхностью. Плоскость, проходящая через заданную прямую линию параллельно световому лучу называется лучевой плоскостью. Тень от прямой линии может быть точкой, прямой, ломаной или кривой.
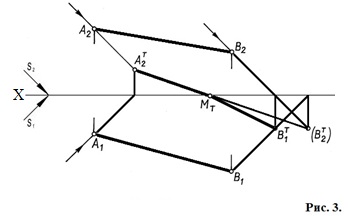
Построение тени отрезка прямой на две плоскости проекций ведется в следующей последовательности:
1. Тень отрезка на одну из плоскостей строят, предполагая, что второй не существует. В примере на рис. 3 сначала построена тень отрезка на фронтальную плоскость проекций.
2. Если построенная тень пересекает ось проекций, то в этой точке тень преломляется и с одной плоскости проекций переходит на другую. В эту точку и будет направлена преломившаяся тень отрезка прямой. На рис. 3 такой точкой является реальная тень точки В на горизонтальной плоскости проекций.
Закономерности расположения теней отрезков прямых частного положения:
· Если отрезок прямой параллелен плоскости, то тень от него на эту плоскость параллельна отрезку и равна ему по величине.
· Если прямая перпендикулярна к плоскости, то тень, падающая от неё на эту плоскость, совпадает с проекцией светового луча на этой плоскости.
· Если прямая параллельна направлению светового луча, то тень от неё – точка.
· Параллельные прямые имеют параллельные тени.
Тень плоских фигур
Построение теней плоской фигуры упрощается в тех случаях (см. рис. 4), когда точка или принадлежащая ей прямая, расположена в плоскости проекций, потому, что точки B и C или прямая BC совпадают со своей тенью.
Тень четырехугольника, занимающего общее положение.
Чтобы построить падающую тень плоской фигуры четырехугольника ABCD, занимающего общее положение (см. рис. 5), когда его вершины и стороны не принадлежат плоскостям проекций, нужно найти тени от каждой его вершины, соединив между собой прямыми линиями одноименные тени точек.
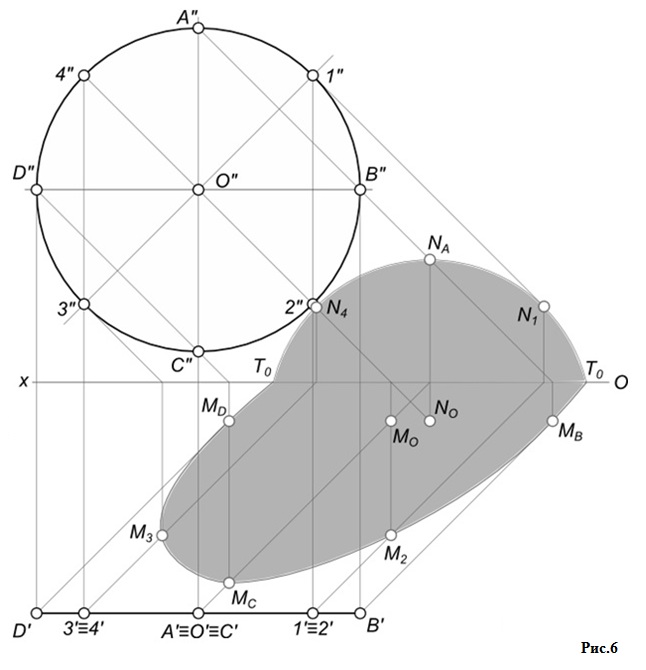
При построении тени круга, расположенного параллельно фронтальной плоскости проекций (см. рис. 6), разделяем круг на 8 равных частей и находим тени всех этих точек, которые соединяем плавной кривой. На фронтальной плоскости проекций достаточно найти тень от центра круга, которая послужит центром для проведения окружности, служащей контуром падающей тени от круга.
Тени геометрических тел
Построение тенипрямого параллелепипеда, стоящего на горизонтальной плоскости проекций (см. рис. 7).
Построение тенипрямого кругового цилиндра, стоящего на горизонтальной плоскости проекции.
Чтобы построить контур собственной тени поверхности цилиндра (см. рис. 8), необходимо провести к этой поверхности касательные лучевые плоскости, параллельные направлению лучей света, и найти линии касания (образующие цилиндра). Вдоль этих образующих пройдет контур собственной тени.
Контур падающей тени от цилиндра состоит из падающих теней от образующих 2 и 4 и падающей тени от полуокружности DAB.
Построение тенипрямого кругового конуса, стоящего на горизонтальной плоскости проекций.
В данном случае (см. рис. 9), тень основания конуса совпадает с ним, остается найти тени только от вершины конуса, которые падают на фронтальную плоскость проекции в точку NS и горизонтальную плоскость проекции в точку MS. Из точки MS проводим прямые касательные окружности основания и находим на ней точки A`≡MA и B`≡MB, соединив которые с вершиной конуса S`, получим падающую тень конуса на горизонтальной плоскости проекций.
Падающую тень конуса на фронтальную плоскость проекции получим, соединив точки преломления T0 и NS.

· через центр шара O проводим луч света и находим его следы MO и NO на плоскостях проекций;
· через центр шара O, перпендикулярно световым лучам, проводим плоскость β, задав ее следами;
· находим линию пересечения поверхности шара с плоскостью β, которая определяет границы собственной тени шара α, применяя для этого перемену плоскости проекции;
· отмечаем на горизонтальной плоскости проекции G` и проведя через точку G вспомогательную горизонтально проецирующую плоскость δΗ находим ее недостающую проекцию G», применяя при этом конкурирующие точки и определение видимости;
· проводим лучи света через центр шара O и точку G находим их следы MO и MG на горизонтальной плоскости проекции, определяющие большую полуось эллипса;
· проводим луч света через точку F, находим ее след на горизонтальной плоскости проекции MF. Отрезок MO MF определяет малую полуось эллипса; выполняем построение эллипса до точек перелома тени;
· аналогично выполняем построение падающей тени от шара на фронтальную плоскость проекции.
Построение теней разновысотных объектов
🎬 Видео
Определение кратчайшей расстоянии от точки до плоскостиСкачать

Параллельность прямых. 10 класс.Скачать

Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

10 класс, 10 урок, Параллельные плоскостиСкачать

Лекция 2. Плоскость. Точка и прямая в плоскости.Скачать

Лекция 8. Тени на комплексном чертеже. Часть 1.Скачать

Построение недостающей проекции плоскости. Принадлежность прямой к плоскостиСкачать

Проецирование прямой общего положенияСкачать

Построение следов плоскостиСкачать

Лекция 8. Тени на комплексном чертеже. Часть 3.Скачать

Определение натуральной величины треугольника АВС методом вращения вокруг горизонтали или фронталиСкачать

Точка встречи прямой с плоскостьюСкачать

Определение истинной величины треугольника АВС. Метод плоско-параллельного перемещенияСкачать

10 класс, 4 урок, Параллельные прямые в пространствеСкачать

Параллельность прямых, плоскостей, прямой и плоскости | Математика ЕГЭ для 10 класса | УмскулСкачать