Тело движется по прямой параллельной оси ох на графике представлена зависимость проекции vx от t

Автомобиль движется по прямой улице, параллельной оси Ox. На графике представлена зависимость проекции его скорости v_x от времени t.

Определите путь, пройденный автомобилем в интервале времени от 5 до 30 с. Ответ дайте в метрах.

Пройденный путь находим как площадь фигуры под графиком зависимости скорости от времени. Представленную фигуру разобьем на две — треугольник и трапецию.

Видео:Тело начинает двигаться из начала координат вдоль оси Ox причем проекция скорости Vx - №22582Скачать

Задание 1 ЕГЭ по физике

Кинематика. Равномерное прямолинейное движение, равноускоренное прямолинейное движение, движение по окружности.

Первое задание ЕГЭ по физике проверяет ваши знания по разделу «Кинематика». Оно относится к базовому уровню, и в нем нет возможности выбора ответа. Для его решения необходимо проанализировать условие задачи, внимательно рассмотреть график зависимости кинематической величины от времени (при наличии такого графика), правильно подобрать формулу, провести расчет и записать ответ в предлагаемых единицах измерения.

Определение кинематических величин по графику

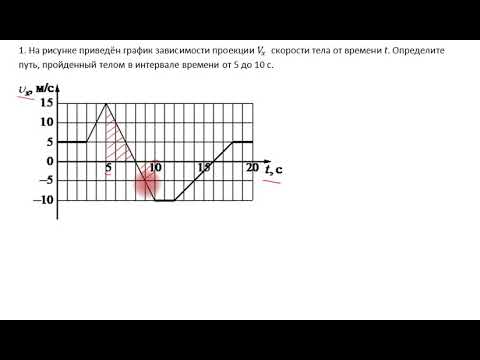
1. На рисунке приведён график зависимости проекции скорости тела от времени t.

Определите проекцию ускорения тела в промежутке времени от 15 до 20 с.

Ответ: _________________________ м/с 2 .Решение:

На графике представлена зависимость проекции скорости от времени. На участке от 15 до 20 с скорость тела изменяется от 10 м/с до -10 м/с. Это говорит о равноускоренном движении, причем проекция ускорения тела должна быть отрицательной. Для решения задачи необходимо воспользоваться формулой для определения проекции ускорения:

Проведем расчет: (м/с 2 ).Полученный результат подтверждает, что движение равноускоренное, причем проекция ускорения отрицательная.

Секрет решения: Долгое время в учебниках физики движение с переменной скоростью делилось на равноускоренное и равнозамедленное Но в последнее время в основном применяют термин «равноускоренное движение», подразумевая постоянство ускорения. Только знак проекции ускорения определяет возрастание или убывание скорости движения тела.

2. На рисунке приведён график зависимости координаты тела x от времени t при его прямолинейном движении по оси x.

Определите проекцию скорости тела в промежутке времени от 25 до 30 с.

Ответ: ___________________________ м/с.

Согласно представленному графику, зависимость координаты тела от времени является линейной. Это указывает на равномерный характер движения тела. Чтобы решить задачу, необходимо воспользоваться формулой для определения скорости при равномерном движении:

Проведем расчет: (м/с)

Проекция скорости получилась отрицательной, и это означает, что в указанный временной интервал тело двигалось в направлении, противоположном выбранной оси Ох.

3. Автомобиль движется по прямой улице вдоль оси Ox. На графике представлена зависимость проекции его скорости от времени.

Определите путь, пройденный автомобилем за 30 с от момента начала наблюдения.

Ответ: _________________________ м.

Так как по условию задачи нам дается график зависимости проекции скорости от времени, то пройденный путь будет определяться площадью геометрической фигуры под графиком. Для вычисления площади получившегося пятиугольника его можно разбить на несколько фигур, например, на две трапеции (см. рис.).

Используя известные формулы для нахождения площади трапеции, можно рассчитать путь за первые 10 с и последующие 20 с (от 10 с до 30 с).

Полученный пятиугольник можно разбить не только на две трапеции. Здесь можно выделить трапецию, прямоугольник и треугольник. Тогда необходимо рассчитывать площади трех фигур и так же их суммировать.

4. На рисунке приведен график зависимости проекции скорости тела, движущегося вдоль оси Ох, от времени.

Определите проекцию перемещения тела за 10 с от начала наблюдения.

Ответ: ________________________ м.

Так же, как в задаче №3, модуль перемещения будет определяться площадью геометрической фигуры под графиком. Но проекция перемещения за время от 0 до 6 с будет положительной, а от 6 до 10 с отрицательной. Общая проекция перемещения будет определяться их суммой.

При расчете можно получить положительное число, но надо помнить, что в интервале от 6 до 10 с тело движется в направлении, противоположном оси Ох. Это означает, что проекция перемещения будет отрицательной. Пройденный путь за указанное время от 0 до 10 с определяется суммой модулей проекций перемещений и будет равным 60 м.

Относительность движения

5. Из двух городов навстречу друг другу с постоянной скоростью движутся два автомобиля. На графике показана зависимость расстояния между автомобилями от времени. Скорость второго автомобиля 25 м/с. С какой скоростью движется первый автомобиль?

Ответ: ________________________ м/с.

Формула для нахождения относительной скорости в векторной форме имеет вид:

Если два тела движутся навстречу друг другу, то в проекциях на ось оХ это уравнение выглядит следующим образом:

С учетом данных графика можно рассчитать относительную скорость этих автомобилей при движении навстречу друг другу. Это происходит на интервале от 0 до 60 мин.

, скорость первого автомобиля

В курсе математики при изучении движения двух тел вводятся понятия «скорость сближения» и «скорость удаления». В первом случае скорости тел суммируются, во втором вычитаются. Эти действия основаны на знаках проекций скоростей движущихся тел. Действия с векторами и их проекциями на оси координат используются как в физике, так и в математике.

6. Два точечных тела начинают двигаться из одной точки вдоль оси OX в противоположных направлениях. На рисунке показаны графики зависимостей проекций их скоростей Vx на ось OX от времени t. Чему будет равно расстояние между этими телами через 8 секунд после начала движения?

Ответ: ___________________________ м.

Эта задача является комбинированной. Для её решения необходимо воспользоваться материалом двух тем: «Определение кинематических величин по графику» и «Относительность движения». Для определения проекций перемещений тел за 8 с необходимо рассчитать площади фигур под графиком.

Знак «минус» для показывает, что тела движутся в противоположных направлениях. Поэтому расстояние между ними через 8 с равно сумме модулей перемещений.

Секрет решения:. Самое главное в этой задаче – выяснить, в каких направлениях двигаются тела. Для этого надо уметь извлекать информацию из графических зависимостей, другими словами, надо уметь «читать» графики. Это умения необходимы почти во всех разделах физики.

7. Катер плывёт по прямой реке, двигаясь относительно берега перпендикулярно береговой линии. Модуль скорости катера относительно берега равен 6 км/ч. Река течёт со скоростью 4,5 км/ч. Чему равен модуль скорости катера относительно воды?

Ответ: ___________________________ км/ч

Решение задачи удобно сопроводить чертежом или рисунком. Выберем направление скорости реки вправо. Тогда катеру необходимо держать курс немного левее, чтобы двигаться перпендикулярно береговой линии.

Векторы собственной скорости катера, скорости течения реки и скорости катера относительно береговой линии образуют прямоугольный треугольник. Запишем для него теорему Пифагора:

Равномерное движение тел по окружности

8. Установленная на станке фреза равномерно вращается с частотой 600 оборотов в минуту. Чему равен модуль ускорения точек, находящихся на расстоянии 3 см от оси фрезы? Ответ округлите до целого числа.

Ответ: ___________________________ м/с 2 .

Так как тело движется равномерно по окружности, то найти требуется центростремительное ускорение. Его можно рассчитать по формуле: Линейная скорость v связана с угловой w соотношением Подставляя это выражение в первое уравнение и проводя сокращения, получим При частоте вращения 600 оборотов в минуту тело будет совершать 10 оборотов за секунду.

Проведем расчет:

В теме «Равномерное движение тел по окружности» достаточно много формул, которые трудно запоминаются. Из них надо знать базовые, которые относятся к периоду, частоте, линейной скорости, угловой скорости и центростремительному ускорению. Все остальные можно получить через достаточно простые рассуждения и выводы.

9. Две шестерни, сцепленные друг с другом, вращаются вокруг неподвижных осей. Большая шестерня радиусом 20 см делает 20 оборотов за 10 секунд. Сколько оборотов в секунду делает меньшая шестерня радиусом 10 см?

Ответ: ___________________________ Гц.

Так как шестерни касаются друг друга, это условие говорит о равенстве линейных скоростей этих тел. Выразим скорости вращения через радиусы и периоды обращения.

Приравняем скорости и проведем сокращения.

с учетом того, что период и частота величины обратные, запишем следующее равенство:

Проведем расчет: (Гц).

В задачах подобного типа всегда надо искать физическую величину, которая является общей для нескольких тел. В данной задаче – это скорость вращения обеих шестерней. Но надо иметь ввиду, что частоты их вращения и угловые скорости различны.

10. Волчок, вращаясь с частотой 20 с -1 , свободно падает с высоты 5 м. Сколько оборотов сделает волчок за время падения?

Ответ: ___________________________ оборотов.

Вначале определим время падения волчка с высоты 5 м. Так как он падает свободно, то начальную скорость будет равна 0. Тогда высота и время падения будут связаны формулой отсюда Проведем расчет времени падения: (с). Так как волчок вращается с частотой 20 то это означает, что за 1 секунду он делает 20 оборотов. Так как время падения составляет 1 с, то количество оборотов также равно 20.

Секрет решения: Эта задача — комбинированная. В ней связаны два раздела кинематики: «Равноускоренное движение» и «Равномерное движение тел по окружности». Надо знать, что суть формул при движении тел с ускорением по горизонтали или по вертикали под действием силы тяжести не меняется. Главное — не ошибиться со знаками проекций для скорости и ускорения.

Видео:На рисунке приведён график зависимости проекции Vx скорости тела от времени t - №22677Скачать

ЕГЭ-физика. Прототипы задания №1 «Кинематика»

Видео:1 задание 1 варианта ЕГЭ 2020 по физике М.Ю. Демидовой (30 вариантов)Скачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

ЕГЭ ФИЗИКА Задание №1 Тема: «Кинематика»

1. На рисунке приведён график зависимости проекции скорости тела vx от времени t.

Определите проекцию ускорения этого тела ax в интервале времени от 0 до 10 с.

2. По графику зависимости модуля скорости тела от времени (см. рисунок) определите ускорение прямолинейно движущегося тела в момент времени 2 с.

3. Координата тела меняется с течением времени согласно закону x = 4 — 2t, где все величины выражены в СИ. Определите проекцию скорости vx этого тела.

4. Координата тела x меняется с течением времени согласно закону x = 2 — 4t + t^2, где все величины выражены в СИ. Определите проекцию ускорения ax этого тела.

5. На рисунке приведён график зависимости проекции скорости тела vx от времени t.

Какой путь прошло это тело в интервале времени от 10 до 15 с?

6. На рисунке представлен график зависимости пути S, пройденного материальной точкой, от времени t. Определите скорость материальной точки в интервале времени от 1 до 3 секунд.

7. На рисунке представлен график зависимости модуля скорости v автомобиля от времени t. Определите по графику путь, пройденный автомобилем в интервале времени от 0 до 30 с.

8. На рисунке представлены графики зависимости пройденного пути от времени для двух тел. Определите, во сколько раз скорость второго тела v2 больше скорости первого тела v1.

9. На графике приведена зависимость проекции скорости тела от времени при прямолинейном движении по оси х. Определите модуль ускорения тела.

10. На графике приведена зависимость проекции скорости тела от времени при прямолинейном движении по оси х. Определите ускорение тела.

11. Автомобиль движется по прямой улице. На графике представлена зависимость скорости автомобиля от времени.

Определите модуль минимального ускорения автомобиля за время наблюдения.

12. На рисунке представлен график зависимости пути S материальной точки от времени t. Определите скорость материальной точки на интервале времени от 5 до 7 с.

13. На рисунке представлен график движения автобуса из пункта А в пункт Б и обратно. Пункт А находится в точке х = 0, а пункт Б — в точке х = 30 км. Чему равна скорость автобуса на пути из Б в А?

14. На рисунке представлен график зависимости пути S, пройденного материальной точкой, от времени t. Определите максимальную скорость точки за время наблюдения.

15. На рисунке приведён график зависимости проекции скорости тела vx от времени.

Определите модуль ускорения этого тела а в интервале времени от 5 до 10 с.

16. На рисунке представлен график зависимости координаты х велосипедиста от времени t. Определите проекцию скорости велосипедиста на ось Ох в интервале времени от 10 до 20 с.

ЕГЭ ФИЗИКА Задание №1 Кинематика. Решение

Из рисунка видно, что от 0 до 10 с тело равномерно набирало скорость. Это возможно только при постоянном ускорении. Следовательно, на этом интервале тело имело постоянное ускорение, равное м/с2.

В промежутке времени от 0 до 3 секунд тело линейно набирает скорость, то есть движется равноускоренно. Ускорение на этом промежутке времени можно найти как м/с2.

Скорость тела – это производная пути по времени, то есть м/с.

Таким образом, проекция скорости будет представлять собой прямую линию параллельную оси t на уровне -2 по оси vx.

Ускорение – это скорость изменения скорости, то есть производная от скорости. Скорость – это производная пути по времени. Используя функцию изменения координаты x найдем сначала проекцию скорости ,

а затем, проекцию ускорения: м/с2.

В интервале времени от 10 до 15 с имеем линейный график скорости, то есть тело двигалось с постоянным ускорением. Величина ускорения равна м/с2. Используя формулу равноускоренного движения

,

получаем (при см. график), что пройденный путь равен

метров.

Скорость определяется выражением . На интервале времени от 1 до 3 секунд из графика видно, что м, а секунды. Следовательно, скорость равна м/с.

Из графика видно, что на интервале времени от 0 дл 10 с тело двигалось равноускоренно с ускорением м/с2 и начальной скоростью . Следовательно, за первые 10 секунд тело прошло расстояние

метров.

С 10-й по 30-ю секунду тело двигалось с постоянной скоростью 10 м/с, следовательно, оно прошло путь метров.

Таким образом, весь путь составил метров.

На графике представлены линейные зависимости пути S от времени t, следовательно, тела двигались с постоянной скоростью. Скорость тел можно найти по формуле . Для первого тела примем с, которому соответствует м, и скорость равна м/с. Для второго тела выберем с, которому соответствует м, и скорость м/с. Получаем отношение ,то есть скорость второго тела в 1,5 раза больше скорости первого тела.

На графике показано линейное изменение скорости от времени, то есть тело движется равнозамедленно (скорость постепенно уменьшается). В этом случае ускорение тела можно найти как . Из графика видно, что при с, изменение скорости составляет м/с. Следовательно, ускорение тела равно м/с2.

Так как скорость линейно возрастает со временем, то ускорение можно вычислить как . Из рисунка видно, что при с изменение скорости равно м/с и ускорение равно м/с2.

При минимальном ускорении изменение скорости автомобиля также будет наименьшим. Другими словами нужно выбрать участок прямой с наименьшим наклоном к оси времени. Этому соответствует участок времени от 20 до 30 секунд, на котором ускорение равно м/с2.

На интервале от 5 до 7 секунд тело движется равномерно, то есть с постоянной скоростью, следовательно, скорость можно найти как , где метров – путь, пройденный за время секунды:

м/с.

Так как точка Б соответствует x=30 км, а точка А x=0 км, то путь, пройденный из Б в А, это второй линейный сегмент на графике, начиная с t=0,5 ч и заканчивая t=1,1 ч. Так как координата x меняется линейно со времен, то скорость автобуса на данном участке была постоянной, следовательно, ее можно найти по формуле , где — расстояние, пройденное за время часа. Подставляя эти величины в формулу скорости, получаем: км/ч.

Чем больше скорость, тем быстрее меняется путь S со временем, то есть для определения максимальной скорости нужно выбрать быстровозрастающий линейный сегмент. Из рисунка видно, что это первый линейный сегмент, на котором скорость была равна м/с.

Из рисунка видно, что на интервале времени от 5 до 10 секунд скорость тела линейно уменьшалась. Это говорит о том, что тело двигалось с постоянным отрицательным ускорением, которое можно найти как . На графике выберем точки, при которых меняется за секунды. Тогда модуль ускорения будет равно м/с2.

В интервале от 10 до 20 секунд координата x линейно изменялась, следовательно, тело имело постоянную скорость. Можно заметить, что эту же скорость можно найти из линейного участка на интервале времени от 10 до 30 секунд по формуле , где , а , и скорость равна м/с.

🎦 Видео

Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Задание 1. Вариант 2. Физика. ЕГЭ по физике 2020. 30 вариантов. Решение и разбор. Тело движется поСкачать

Задача 1. Вариант 1. Физика. ЕГЭ по физике 2020. Решение. Разбор. Демидова. Тело движется по прямойСкачать

Урок 18 (осн). Координаты тела. График движения. График скоростиСкачать

Задача из ЕГЭ по физике │Анализ графика #1Скачать

ЕГЭ по физике. Задание 1. Определение проекции ускоренияСкачать

Графики зависимости пути и скорости от времениСкачать

Графики зависимости кинематических величин от времени при равномерном и равноускоренном движенииСкачать

Решение графических задач на равномерное движениеСкачать

Тело массой 2 кг движется вдоль оси Ox. На рисунке представлен график зависимости проекции - №26477Скачать

Урок 14. Графическое описание РПДСкачать

ЕГЭ по физике. Задание 1. Определение пройденного пути по графику скоростиСкачать

Физика 7 кл (2013 г) Пер §17 Упр 4 №4 . График зависимости скорости равномерного движения тела от врСкачать

Урок 25. График скорости РУД. Перемещение при РУД.Скачать

На рисунке представлен график зависимости модуля скорости тела от времени - №22577Скачать

Графики в механике | ФИЗИКА ЕГЭСкачать