Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 83°. Найдите величину угла OMK. Ответ дайте в градусах.
Угол, образованный хордой и касательной равен половине дуги, которую он заключает, поэтому величина дуги MK равна 2 · 83° = 166°. Угол MOK — центральный, поэтому он равен величине дуги, на которую опирается. Значит, угол MOK равен 166°. В треугольнике OMK стороны OK и OM равны как радиусы окружности, поэтому треугольник OMK — равнобедренный, следовательно, углы при основании равны. Сумма углов треугольника равна 180°, поэтому ∠OKM = ∠OMK = (180° − ∠KOM)/2 = (180° − 166°)/2 = 7°.
Приведём другое решение.
Найдём угол OKM: OKM = 90° − 83° = 7°. Треугольник OMK — равнобедренный, поэтому угол OMK равен углу OKM и равен 7°
Видео:Касательные к окружности с центром O в точках A и B ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Задание №1205
Видео:Через точку A, лежащую вне окружности, проведены две прямые.Скачать

Условие
Две окружности касаются внешним образом в точке P . Прямая MN касается первой окружности в точке M , а второй — в точке N .
а) Докажите, что triangle MNP прямоугольный.
б) Найдите площадь triangle MNP, если известно, что радиусы окружностей равны 4 и 16 .
Видео:Геометрия Прямая AB касается окружности с центром O в точке C, AC = BC. Докажите, что OA = OBСкачать

Решение
а) Пусть O_1 и O_2 — центры касающихся окружностей. Через точку P проведём общую касательную заданных окружностей и обозначим через Q точку пересечения этой касательной с прямой MN .
По свойству касательных, проведённых к окружности, будем иметь: QM=QP, QN=QP. Значит, точки M , N и P равноудалены от точки Q , следовательно, angle MPN является вписанным в некоторую окружность с центром в точке Q и радиусом R=MQ. При этом angle MPN опирается на диаметр MN , а значит, angle MPN=90^. Отсюда triangle MNP является прямоугольным.
б) Пусть O_1 — центр окружности радиуса 4 , а O_2 — центр окружности радиуса 16 .
Рассмотрим MNO_2O_1: прямая MN — касательная к исходным окружностям, O_1M и
O_2N — радиусы, следовательно, O_1M perp MN и O_2N perp MN. Отсюда O_1M parallel O_2N, а значит MNO_2O_1 — прямоугольная трапеция.
Точка касания двух окружностей лежит на линии их центров, поэтому отрезок
O_1O_2 пересекает касательную PQ в точке P , следовательно, O_1P=O_1M=4, O_2P=O_2N=16, O_1O_2=O_1P+O_2P=4+16=20.
Проведём из точки P перпендикуляр PH к отрезку MN .
Приведем отрезок O_1Kperp NO_2, Kin NO_2, получим прямоугольник MNKO_1, в котором MN=O_1K и KN=O_1M=4, а также прямоугольный triangle O_1KO_2, в котором KO_2=NO_2-NK=16-4=12.
Следовательно, по теореме Пифагора O_1K= sqrt = sqrt = 16, MN-O_1K=16.
MH равна высоте треугольника MPO_1, опущенной на сторону MO_1.
NH равна высоте треугольника NPO_2, опущенной на сторону NO_2.
Видео:✓ Простое решение красивой геометрии | Планиметрия | Физтех-2021. Математика | Борис ТрушинСкачать

Окружность. Касательная к окружности.
Прямая (MN), имеющая с окружностью только одну общую точку (A), называется касательной к окружности.
Общая точка называется в этом случае точкой касания.
Возможность существования касательной, и притом проведенной через любую точку окружности, как точку касания, доказывается следующей теоремой.
Теорема.
Если прямая перпендикулярна к радиусу в его конце, лежащем на окружности, то эта прямая — касательная.
Пусть O — центр некоторого круга и OA какой-нибудь его радиус. Через его конец A проведем MN ⊥ OA.Требуется доказать, что прямая MN — касательная, т.е. что эта прямая имеет с окружностью только одну общую точку A.
Допустим противное: пусть MN имеет с окружностью еще другую общую точку, например B. Тогда прямая OB была бы радиусом и, следовательно, равнялась бы OA.
Но этого быть не может, так как, если OA — перпендикуляр, то OB должна быть наклонной к MN, а наклонная больше перпендикуляра.
Обратная теорема.
Если прямая касательная к окружности, то радиус, проведенный в точку касания, перпендикулярен к ней.
Следствие.
Через всякую данную на окружности точку можно провести касательную к этой окружности и притом только одну, так как через эту точку можно провести перпендикуляр, и притом только один, к радиусу, проведенному в нее.
Теорема.
Касательная параллельная хорде, делит в точке касания дугу, стягиваемую хордой, пополам.
Пусть прямая AB касается окружности в точке M и параллельна хорде СD. Требуется доказать, что ∪CM= ∪MD.
Проведя через точку касания диаметр ME, получаем: EM ⊥ AB и следовательно, EM ⊥ СD. Поэтому СM=MD.
Через данную точку провести касательную к данной окружности.
Если данная точка находится на окружности, то проводят через нее радиус и через конец радиуса перпендикулярную прямую. Эта прямая будет искомой касательной.
Рассмотрим тот случай, когда точка дана вне круга.
Пусть требуется провести к окружности с центром O касательную через точку A. Для этого из точки A, как из центра, описываем дугу радиусом AO, а из точки O, как центра, пересекаем эту дугу в точках B и С раствором циркуля, равным диаметру данного круга.
Проведя затем хорды OB и OС, соединим точку A с точками D и E, в которых эти хорды пересекаются с данной окружностью. Прямые AD и AE — касательные к окружности O. Действительно, из построения видно, что треугольники AOB и AOС равнобедренные (AO = AB =AС) с основаниями OB и OС, равными диаметру круга O.
Так как OD и OE — радиусы, то D — середина OB, а E — середина OС, значит AD и AE — медианы, проведенные к основаниям равнобедренных треугольников, и потому перпендикулярны к этим основаниям. Если же прямые DA и EA перпендикулярны к радиусам OD и OE, то они — касательные.
Следствие.
Две касательные, проведенные из одной точки к окружности, равны и образуют равные углы с прямой, соединяющей эту точку с центром.
Так AD=AE и ∠OAD = ∠OAE потому, что прямоугольные треугольники AOD и AOE, имеющие общую гипотенузу AO и равные катеты OD и OE (как радиусы), равны. Заметим, что здесь под словом “касательная” подразумевается собственно “отрезок касательной” от данной точки до точки касания.
🔍 Видео
Всё про углы в окружности. Геометрия | МатематикаСкачать

№1,17 | Все теория по планиметрии за 4 часа | Решаем все прототипы №1 из ФИПИСкачать

На окружности отмечены точки A и B так, что меньшая дуга AB равна 92 градуса. Прямая BC касается окрСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

#32. Регион ВсОШ 2023, 9.8Скачать

Уравнение окружности (1)Скачать

Профильный ЕГЭ 2024. Задача 16. Касающиеся окружностиСкачать

Отрезки касательных из одной точки до точек касания окружности равны | Окружность | ГеометрияСкачать

2023 На окружности с центром в точке О отмечены точки А и Б так что угол аоб равен 45Скачать

Геометрия Вписанная окружность треугольника ABC касается сторон AB BC и AC в точках M N и KСкачать

Окружность касается. Красота неземная! ЕГЭ, ЦТ, ЗНО!Скачать

Параметр. Серия 12. Решение задач с окружностями. Касание окружности и прямойСкачать

🔴 В окружности с центром O отрезки AC и BD ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать

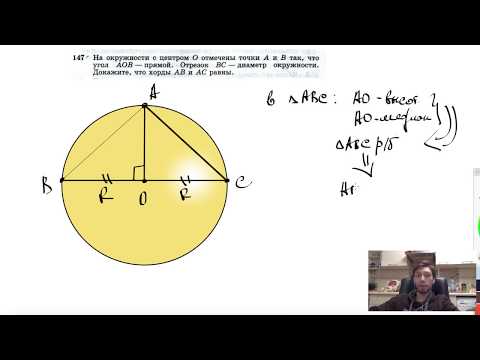
№147. На окружности с центром О отмечены точки А и В так, что угол АОВ — прямой. Отрезок ВССкачать
ОГЭ. Математика. Задание 26 | Прямоугольная трапеция и окружность | Борис Трушин |Скачать

Точка O – центр окружности, на которой лежат точки ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

