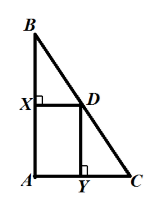Замечательные точки треугольника не просто так описываются таким прилагательным. Для многих учеников, а начинают знакомиться с этим понятием в 8 классе, эта тема кажется наиболее интересной и простой в курсе геометрии, поэтому многочисленные теоремы и свойства запоминаются достаточно просто.
Итак, какие же четыре точки называются замечательными? Перечислим их:
точку пересечения медиан треугольника;
точку пересечения биссектрис треугольника;
точку пересечения высот треугольника;
точку пересечения серединных перпендикуляров сторон треугольника.
Все точки обладают своими особенностями и свойствами, про всех есть свои теоремы и следствия из них. Кроме того, существует свойство, которое справедливо сразу для четырёх этих точек. Вне зависимости от того, медиана ли это, биссектриса или высота, все они пересекаются в одной точке.
Замечательные точки характерны не только для треугольников. Например, в трапеции так же четыре замечательные точки.
Теперь рассмотрим основные положения, связанные с замечательными точками треугольника.
- Точка пересечения медиан треугольника
- Точка пересечения биссектрис треугольника
- Точка пересечения высот треугольника
- Пример решения задач с построением
- Ззамечательные точки треугольника — свойства, применение и примеры решения
- Точка пересечения медиан треугольника
- Точка пересечения биссектрис треугольника
- Четыре замечательные точки треугольника
- Точка пересечения медиан треугольника
- Точка пересечения биссектрис треугольника
- Готовые работы на аналогичную тему
- Точка пересечения серединных перпендикуляров треугольника
- Точка пересечения высот треугольника
- Пример задачи на использование 4 замечательных точек треугольника
- 🎬 Видео
Видео:Урок по теме ЧЕТЫРЕ ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИ ТРЕУГОЛЬНИКА ГЕОМЕТРИЯ 8 КЛАСССкачать

Точка пересечения медиан треугольника
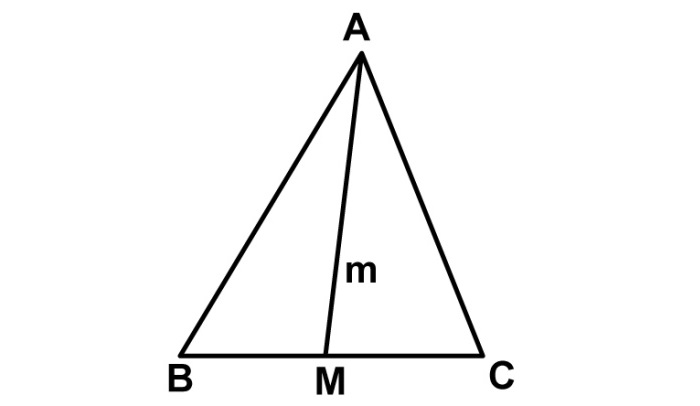
Из курса геометрии известно определение медианы треугольника.
На данном рисунке она обозначена прямой m, которая исходит из вершины А и заканчивается точкой М, являющейся центром стороны ВС.
Теперь сделаем чертёж треугольника, на котором укажем замечательную точку пересечения медиан.
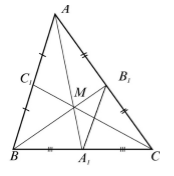
Для начала постройте абсолютно любой треугольник и обозначьте его буквами А, В и С.
На отрезке АВ отметьте центр С1, на стороне ВС центр А1, на АС центр В1.
Проведите 3 медианы из вершин. Из угла А – медиана АА1,из угла В — медиана ВВ1, из угла С — медиана СС1.
Должно получиться так, как показано на рисунке: три проведённые линии пересекаются в одной точке G (что является их свойством).
Изучим следующее свойство точки пересечения трёх медиан треугольника.
Отрезки медианы треугольника, разделённой замечательной точкой, относятся друг к другу как 2:1. Проследим это свойство на примере используемого нами рисунка:
A1G = 2AG, B1G = 2BG, C1G = 2CG.
Видео:Замечательные точки треуг-ка. 8 класс.Скачать

Точка пересечения биссектрис треугольника
Прежде чем мы приступим к изучению следующей точки, рассмотрим теорему о биссектрисе, проведённой из вершины неразвёрнутого угла, и докажем её.
Рассмотрим пример. Дано:
угол ВАС Точка пересечения серединных перпендикуляров сторон треугольника
Для начала вспомним определение серединного перпендикуляра. Теорема о серединном перпендикуляре:
Сделаем краткое доказательство. Соединим концы отрезка с вершиной серединного отрезка. Докажем равенство полученных треугольников, из чего следует АD = DB.
Построим эту точку.
В треугольнике АВС отмечаем середины его сторон. Проводим три серединных перпендикуляра КО, LO, МО и отмечаем точку их пересечения О.
Видео:Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

Точка пересечения высот треугольника
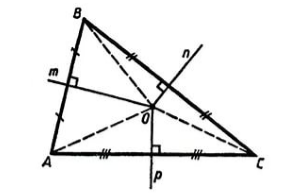
Проведём три высоты в ∆АВС, все они пересекутся в т. Н. Точка Н по отношению к ∆АВС – ортоцентр.
Свойство высот треугольника:
если все три высоты треугольника или их продолжения пересекаются в одной точке, то это ортоцентр;
СH * HНС
= АH * АНА = ВH * ВНВ.
Ортоцентр может располагаться внутри треугольника, снаружи или совпадать с одной из вершин.
На рисунке показано расположение ортоцентра в остроугольном, прямоугольном и тупоугольном треугольниках.
Видео:Геометрия 8 класс. Четыре замечательные точки треугольникаСкачать

Пример решения задач с построением
Замечательные точки треугольника замечательные именно потому, что они имеют много полезных для решения задач свойств. Рассмотрим пример решения задачи на эту тему.
Серединный перпендикуляр в ∆АВС, опущенный к АС, пересекает ВС в т. В. Найти BD, DC, если AD = 5 см BC = 9 см.
Сделаем дополнительное построение – серединный отрезок КD к прямой АС. Тогда DK это и высота, и медиана в ∆АВС. Если в треугольнике проведена прямая, которая является высотой и медианой, то он равнобедренный. Значит, AD = DC = 5 см.
ВD =ВС — DC = 4 см.
Ответ: DC = 5 см, ВD = 4 см.
Видео:Замечательные точки треугольника. Медиана треугольника.Скачать

Ззамечательные точки треугольника — свойства, применение и примеры решения
Замечательные точки треугольника не просто так описываются таким прилагательным. Для многих учеников, а начинают знакомиться с этим понятием в 8 классе, эта тема кажется наиболее интересной и простой в курсе геометрии, поэтому многочисленные теоремы и свойства запоминаются достаточно просто.
Итак, какие же четыре точки называются замечательными? Перечислим их:
точку пересечения медиан треугольника;
точку пересечения биссектрис треугольника;
точку пересечения высот треугольника;
точку пересечения серединных перпендикуляров сторон треугольника.
Все точки обладают своими особенностями и свойствами, про всех есть свои теоремы и следствия из них. Кроме того, существует свойство, которое справедливо сразу для четырёх этих точек. Вне зависимости от того, медиана ли это, биссектриса или высота, все они пересекаются в одной точке.
Замечательные точки характерны не только для треугольников. Например, в трапеции так же четыре замечательные точки.
Теперь рассмотрим основные положения, связанные с замечательными точками треугольника.
Видео:четыре замечательные точки треугольника 8 КЛАСС АтанасянСкачать

Точка пересечения медиан треугольника
Из курса геометрии известно определение медианы треугольника.
На данном рисунке она обозначена прямой m, которая исходит из вершины А и заканчивается точкой М, являющейся центром стороны ВС.
Теперь сделаем чертёж треугольника, на котором укажем замечательную точку пересечения медиан.
Для начала постройте абсолютно любой треугольник и обозначьте его буквами А, В и С.
На отрезке АВ отметьте центр С1, на стороне ВС центр А1, на АС центр В1.
Проведите 3 медианы из вершин. Из угла А – медиана АА1,из угла В — медиана ВВ1, из угла С — медиана СС1.
Должно получиться так, как показано на рисунке: три проведённые линии пересекаются в одной точке G (что является их свойством).
Изучим следующее свойство точки пересечения трёх медиан треугольника.
Отрезки медианы треугольника, разделённой замечательной точкой, относятся друг к другу как 2:1. Проследим это свойство на примере используемого нами рисунка:
Видео:ГЕОМЕТРИЯ 8 класс: 4 замечательные точкиСкачать

Точка пересечения биссектрис треугольника
Прежде чем мы приступим к изучению следующей точки, рассмотрим теорему о биссектрисе, проведённой из вершины неразвёрнутого угла, и докажем её.
Видео:Четыре замечательные точки треугольникаСкачать

Четыре замечательные точки треугольника
Вы будете перенаправлены на Автор24
В треугольнике есть так называемые четыре замечательные точки: точка пересечения медиан. Точка пересечения биссектрис, точка пересечения высот и точка пересечения серединных перпендикуляров. Рассмотрим каждую из них.
Видео:3 свойства биссектрисы #shortsСкачать

Точка пересечения медиан треугольника
О пересечении медиан треуголника: Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении $2:1$ начиная с вершины.
Доказательство.
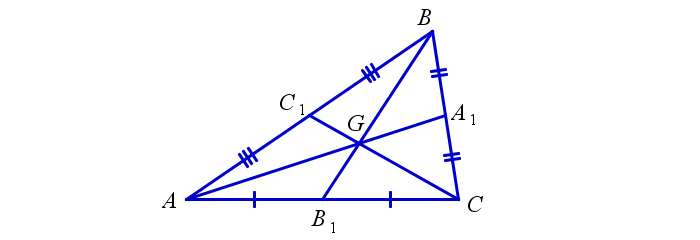
Рассмотрим треугольник $ABC$, где $_1, _1, _1$ его медианы. Так как медианы делят стороны пополам. Рассмотрим среднюю линию $A_1B_1$ (Рис. 1).
Рисунок 1. Медианы треугольника
По теореме 1, $AB||A_1B_1$ и $AB=2A_1B_1$, следовательно, $angle ABB_1=angle BB_1A_1, angle BAA_1=angle AA_1B_1$. Значит треугольники $ABM$ и $A_1B_1M$ подобны по первому признаку подобия треугольников. Тогда
Аналогично доказывается, что
Видео:Замечательные точки треугольникаСкачать

Точка пересечения биссектрис треугольника
О пересечении биссектрис треугольника: Биссектрисы треугольника пересекаются в одной точке.
Доказательство.
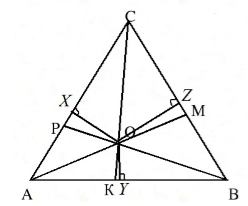
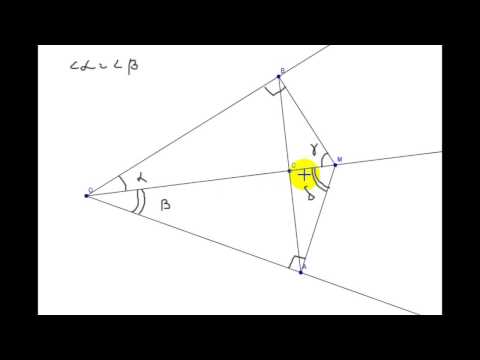
Рассмотрим треугольник $ABC$, где $AM, BP, CK$ его биссектрисы. Пусть точка $O$ — точка пересечения биссектрис $AM и BP$. Проведем из этой точки перпендикуляры к сторонам треугольника (рис. 2).
Рисунок 2. Биссектрисы треугольника
Готовые работы на аналогичную тему
Для доказательства нам потребуется следующая теорема.
Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.
По теореме 3, имеем: $OX=OZ, OX=OY$. Следовательно, $OY=OZ$. Значит точка $O$ равноудалена от сторон угла $ACB$ и, значит, лежит на его биссектрисе $CK$.
Видео:Геометрия. 8 класс. Замечательные точки треугольника /27.10.2020/Скачать

Точка пересечения серединных перпендикуляров треугольника
Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
Доказательство.
Пусть дан треугольник $ABC$, $n, m, p$ его серединные перпендикуляры. Пусть точка $O$ — точка пересечения серединных перпендикуляров $n и m$ (рис. 3).
Рисунок 3. Серединные перпендикуляры треугольника
Для доказательства нам потребуется следующая теорема.
Каждая точка серединного перпендикуляра к отрезку равноудалена от концов данного отрезка.
По теореме 3, имеем: $OB=OC, OB=OA$. Следовательно, $OA=OC$. Значит точка $O$ равноудалена от концов отрезка $AC$ и, значит, лежит на его серединном перпендикуляре $p$.
Видео:Вторая замечательная точка треугольникаСкачать

Точка пересечения высот треугольника
Высоты треугольника или их продолжения пересекаются в одной точке.
Доказательство.
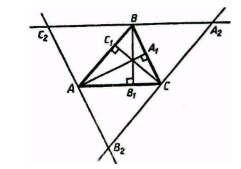
Рассмотрим треугольник $ABC$, где $_1, _1, _1$ его высоты. Проведем через каждую вершину треугольника прямую, параллельную противоположной вершине стороне. Получаем новый треугольник $A_2B_2C_2$ (рис. 4).
Рисунок 4. Высоты треугольника
Так как $AC_2BC$ и $B_2ABC$ параллелограммы с общей стороной, то $AC_2=AB_2$, то есть точка $A$ — середина стороны $C_2B_2$. Аналогично, получаем, что точка $B$ — середина стороны $C_2A_2$, а точка $C$ — середина стороны $A_2B_2$. Из построения мы имеем, что $_1bot A_2B_2, _1bot A_2C_2, _1bot C_2B_2$. Следовательно, $_1, _1, _1$ — серединные перпендикуляры треугольника $A_2B_2C_2$. Тогда, по теореме 4, имеем, что высоты $_1, _1, _1$ пересекаются в одной точке.
Видео:Геометрия. 8 класс. Замечательные точки треугольника /20.10.2020/Скачать

Пример задачи на использование 4 замечательных точек треугольника
Серединные перпендикуляры к сторонам $AB$ и $AC$ треугольника $ABC$ пересекаются в точке $D$ стороны $BC$. Докажите, что
а) точка $D$ — середина стороны $BC$.
б) $angle A=angle B+angle C$
Решение.
а) По теореме 4, все серединные перпендикуляры пересекаются в точке $D$. Следовательно, $D$ — основание серединного перпендикуляра к стороне $BC$. Значит точка $D$ — середина стороны $BC$.
б) Так как $X$ и $D$ — середины сторон, то $XD$ — средняя линия треугольника. Тогда, по теореме о средней линии треугольника $XD||AC$. Значит,$angle A=angle DXB$, как соответственные углы. Значит, $angle A=^0$. Тогда$angle B+angle C=^0-angle A=^0-^0=^0=angle A$
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 29 03 2021
🎬 Видео
Высота, биссектриса, медиана. 7 класс.Скачать

Вторая замечательная точка треугольникаСкачать

Планиметрия | конкретные задачи | замечательные точки треугольников | 2Скачать
Геометрия 8 класс : Решение задач. 4 замечательные точкиСкачать

🔥 Свойства МЕДИАНЫ #shortsСкачать

Геометрия. 8 класс. Замечательные точки треугольника /22.10.2020/Скачать