- теория по физике 🧲 кинематика
- Кинематические характеристики движения
- Горизонтальный бросок тела с горы
- Тело, брошенное горизонтально
- Начальные условия
- Кинематические уравнения движения тела брошенного горизонтально
- Время полета, дальность полета тела брошенного горизонтально
- Примеры задач с решением
- Тело брошено горизонтально с начальной скоростью 10 м с через какое время вектор скорости
- 📺 Видео
теория по физике 🧲 кинематика
Если тело бросить горизонтально с некоторой высоты, оно будет одновременно падать и двигаться вперед. Это значит, что оно будет менять положение относительно двух осей: ОХ и ОУ. Относительно оси ОХ тело будет двигаться с постоянной скоростью, а относительно ОУ — с постоянным ускорением.
Видео:Кинематика. Движение тела, брошенного горизонтальноСкачать
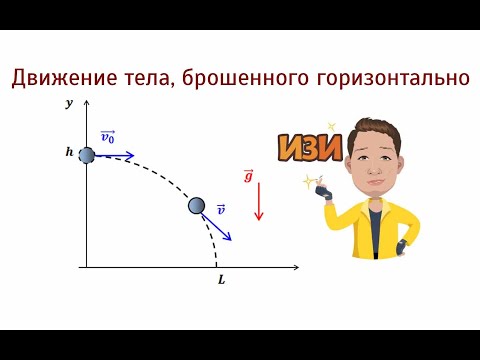
Кинематические характеристики движения
Графически движение горизонтально брошенного тела описывается следующим образом:
- Вектор скорости горизонтально брошенного тела направлен по касательной к траектории его движения.
- Проекция начальной скорости на ось ОХ равна v0: vox = v0. Ее проекция на ось ОУ равна нулю: voy = 0.
- Проекция мгновенной скорости на ось ОХ равна v0: vx = v0. Ее проекция на ось ОУ равна нулю: vy = –gt.
- Проекция ускорения свободного падения на ось ОХ равна нулю: gx = 0. Ее проекция на ось ОУ равна –g: gy = –g.
Модуль мгновенной скорости в момент времени t можно вычислить по теореме Пифагора:
Подставив в эту формулу значения проекций мгновенной скорости в момент времени t, получим:
Минимальная скорость в течение всего времени движения равна начальной скорости: vmin = v0.
Максимальной скорости тело достигает в момент приземления. Поэтому максимальной скоростью тела в течение всего времени движения является его конечная скорость: vmax = v.
Время падения — время, в течение которого перемещалось тело до момента приземления. Его можно выразить через формулу высоты при равноускоренном прямолинейном движении:
h0 — высота, с которой тело бросили в горизонтальном направлении.
Дальность полета — перемещение тела относительно ОХ. Обозначается буквой l. Так как относительно ОХ тело движется с постоянной скоростью, для вычисления дальности полета можно использовать формулу перемещения при равномерном прямолинейном движении:
Выразив время падения через высоту и ускорение свободного падения, формула для определения дальности полета получает следующий
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Горизонтальное смещение тела — смещение тела вдоль оси ОХ. Вычислить горизонтальное смещение тела в любой момент времени t можно по формуле координаты x:
Учитывая, что x0 = 0, и проекция ускорения свободного падения на ось ОХ тоже равна нулю, а проекция начальной скорости есть модуль этой скорости, данная формула принимает вид:
Мгновенная высота — высота, на которой находится тело в выбранный момент времени t. Она вычисляется по формуле координаты y:
Пример №1. Из окна, расположенного 5 м от земли, горизонтально брошен камень, упавший на расстоянии 8 м от дома. С какой скоростью был брошен камень?
Так как нам известна высота места бросания и дальность полета, начальную скорость тела можно вычислить по формуле:
Выразим начальную скорость и вычислим ее:
Видео:Урок 37. Движение тела, брошенного под углом к горизонту (начало)Скачать

Горизонтальный бросок тела с горы
Горизонтальный бросок тела с горы — частный случай горизонтального броска. От него он отличается увеличенным расстоянием между местом бросания и местом падения. Это увеличение появляется потому, что плоскость находится под наклоном. И чем больше этот наклон, тем больше времени требуется телу, чтобы приземлиться.
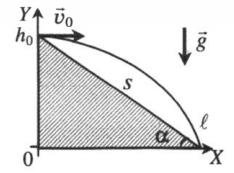
График горизонтального броска тела с горы
α — угол наклона плоскости к горизонту, s — расстояние от места бросания до места падения
Дальность полета — смещение тела относительно оси ОХ от места бросания до места падения. Она равна произведению расстояния от места бросания до места падения и косинуса угла наклона плоскости к горизонту:
Начальная высота — высота, с которой было брошено тело. Обозначается h0. Начальная высота равна произведению расстояния от места бросания до места падения и синусу угла наклона плоскости к горизонту:
Пример №2. На горе с углом наклона 30 о бросают горизонтально мяч с начальной скоростью 15 м/с. На каком расстоянии от точки бросания вдоль наклонной плоскости он упадет?
Выразим это расстояние через дальность полета:
Дальность полета выражается по формуле:
Подставим ее в формулу для вычисления расстояния от точки бросания до точки падения:
Выразим с учетом формулы начальной высоты:
Поделим обе части выражения на общий множитель s:
Подставим известные значения:
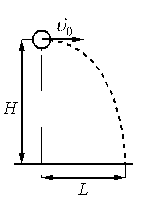
Шарик, брошенный горизонтально с высоты H с начальной скоростью υ 0, за время t пролетел в горизонтальном направлении расстояние L (см. рисунок).
В другом опыте на этой же установке шарик массой 2m бросают со скоростью 2 υ 0.
Что произойдёт при этом с временем полёта, дальностью полёта и ускорением шарика? Сопротивлением воздуха пренебречь. Для каждой величины определите соответствующий характер её изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
- Записать формулы для каждой из величин.
- Определить, как зависит эта физическая величина от начальной скорости и массы.
- Определить характер изменения физической величины при увеличении начальной скорости и массы шарика.
Решение
Время полета тела, брошенного горизонтально, определяется формулой:
Исходя из формулы, время никак не зависит от начальной скорости и массы тела. Поэтому оно при увеличении начальной скорости и массы вдвое никак не изменится.
Дальность полета тела, брошенного горизонтально, определяется формулой:
Исходя из формулы, дальность полета зависит от начальной скорости прямо пропорционально. Поэтому, если начальная скорость тела будет увеличена вдвое, дальность полета тоже увеличится (вдвое). От массы дальность полета никак не зависит.
Ускорение свободного падения — величина постоянная для нашей планеты. Поэтому изменение начальной скорости никак не повлияет на него. Ускорение не изменится.
Значит, верный ответ — 313.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Шарик, брошенный горизонтально с высоты H с начальной скоростью υ 0, за время t пролетел в горизонтальном направлении расстояние L (см. рисунок).
Что произойдёт с временем полёта, дальностью полёта и ускорением шарика, если на этой же установке уменьшить начальную скорость шарика в 2 раза? Сопротивлением воздуха пренебречь. Для каждой величины определите соответствующий характер её изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
- Записать формулы для каждой из величин.
- Определить, как зависит эта физическая величина от начальной скорости.
- Определить характер изменения физической величины при уменьшении начальной скорости.
Решение
Время полета тела, брошенного горизонтально, определяется формулой:
Исходя из формулы, время никак не зависит от начальной скорости. Поэтому оно при уменьшении начальной скорости вдвое не изменится.
Дальность полета тела, брошенного горизонтально, определяется формулой:
Исходя из формулы, дальность полета зависит от начальной скорости прямо пропорционально. Поэтому, если начальная скорость тела будет уменьшена вдвое, дальность полета тоже уменьшится (вдвое).
Ускорение свободного падения — величина постоянная для нашей планеты. Поэтому изменение начальной скорости никак не повлияет на него. Ускорение не изменится.
Значит, верный ответ — 323.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Видео:Физика Тело брошено горизонтально со скоростью 10 м/с. Дальность полета по горизонтали оказаласьСкачать

Тело, брошенное горизонтально
Видео:Движение тела, брошенного под углом к горизонтуСкачать

Начальные условия
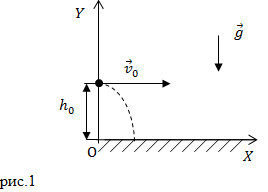
Пусть тело, которое можно считать материальной точкой, бросили с начальной скоростью $<overline>_0 $горизонтально рис.1. с некоторой высоты $h_0.$
Движение тела будем рассматривать в системе отсчета связанной с Землей. Ось X направим горизонтально, ось Y вертикально вверх. Тело будет перемещаться под действием силы тяжести, если не учитывать силу сопротивления воздуха, то других сил нет. Движение тела будет происходить в плоскости, в которой находятся векторы: начальной скорости тела $<overline>_0$ и ускорения свободного падения $overline. $
Запишем начальные условия движения нашей материальной точки:
Вектор ускорения при движении под воздействием силы тяжести считаем постоянным:
где величина ускорения свободного падения равна $gapprox $ 9,8 $frac.$
Видео:Физика 9 класс (Урок№2 - Движение тела, брошенного горизонтально)Скачать

Кинематические уравнения движения тела брошенного горизонтально
Уравнение для скорости равнопеременного движения в поле силы тяжести принимает вид:
где $<overline>_0$ — начальная скорость тела. Движение материальной точки в рассматриваемом случае можно представить сумму двух независимых движений по прямым линиям, в которых участвует тело, брошенное горизонтально. Это равномерное движение с неизменной скоростью $<overline>_0$ в горизонтальном направлении и равноускоренное движение с ускорением $overline$ без начальной скорости в направлении вектора ускорения свободного падения.
В проекциях на оси X и Y имеем:
Величина скорости перемещения частицы равна:
Уравнение для вектора перемещения тела, в нашем случае:
где $<overline>_0$ — смещение тела в начальный момент времени. В нашем случае $s_0=y (t=0)=h_0$. Уравнение (7) даст два скалярных выражения для координат падающей частицы:
Как уже говорилось, каждое из двух отдельных движений тела происходит по прямой, но траекторией движения падающего тела является ветвь параболы, находящаяся в плоскости в которой лежат $<overline>_0$ и $overline$.
Исключив время, как параметр, из системы (8) получим уравнение траектории движения точки:
Максимумом траектории тела в рассматриваемом случае является точка бросания.
Видео:Урок 40. Задачи на движение тела, брошенного под углом к горизонту (ч.1)Скачать

Время полета, дальность полета тела брошенного горизонтально
Время полета тела можно выразить из второго уравнения системы (8), если предположить, что в момент падения ордината точки $y=0$:
Дальность полета (s) — это расстояние, которое тело преодолело по горизонтали (по оси X). Его найдем, подставив время полета в первое уравнение системы (8):
Видео:Теория движения тела брошенного горизонтально . 2021-10Скачать

Примеры задач с решением
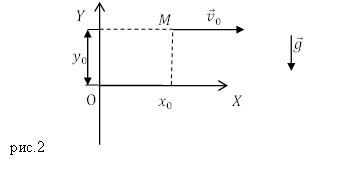
Задание. Напишите уравнения траектории движения материальной точки М для случая, который изображен на рис. 2.
Решение. В качестве основы для решения задачи применим кинематическое уравнение для перемещения при равноускоренном движении материальной точки:
Рассматривая рис.2 запишем проекции векторного уравнения (1.1) на оси системы координат. В проекции на оси X и Y выражение (1.1) превращается в систему скалярных уравнений:
Для того чтобы получить уравнение траектории движения точки М выразим из первого уравнения системы (1.2) время и подставим его во второе уравнение:
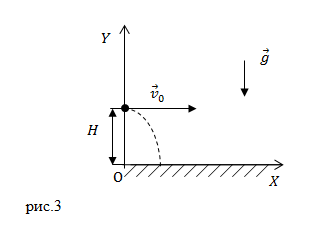
Задание. Вертолет, летевший горизонтально на высоте $H$ со скоростью $v_0$, сбросил груз. За какое время до пролета вертолета над целью он должен сбросить груз, чтобы попасть в цель? Груз считать материальной точкой, сопротивление воздуха не учитывать.
Решение. Сделаем рисунок.
Запишем начальные условия движения груза:
Нам следует найти время полета груза. Зная, что движение груза происходит в поле тяжести Земли, начальные условия заданы (2.1). При этом время полета можно найти, используя формулу, которая получена в теоретической части статьи:
Видео:Движение тела брошенного горизонтально. Теория и решение задачСкачать

Тело брошено горизонтально с начальной скоростью 10 м с через какое время вектор скорости
Персональный блог. Темы: физика, ход солнца, солнечные часы

|
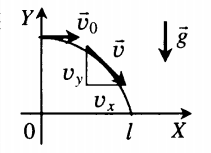
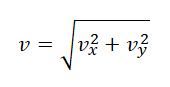
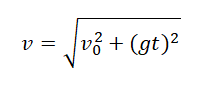
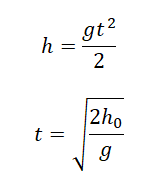
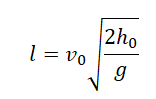
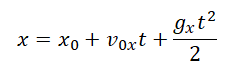
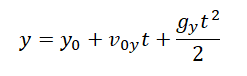
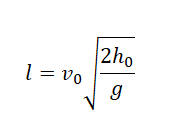
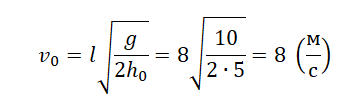
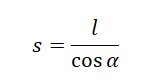
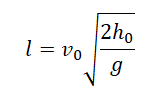
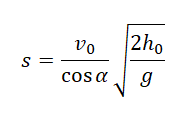
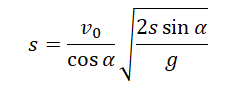
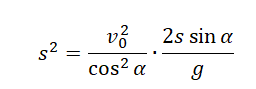
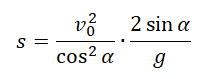
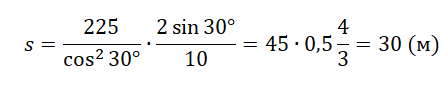

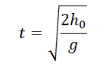
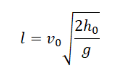
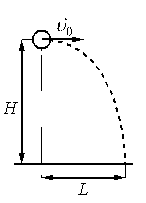

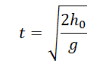
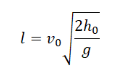






 Полет тела, брошенного под углом к горизонту.
Полет тела, брошенного под углом к горизонту.














