Таблица тангенсов на единичной окружности

В прошлой статье мы познакомились с тригонометрическим кругом и научились находить значения синуса и косинуса основных углов.

Как же быть с тангенсом и котангенсом ? Об этом и поговорим сегодня.

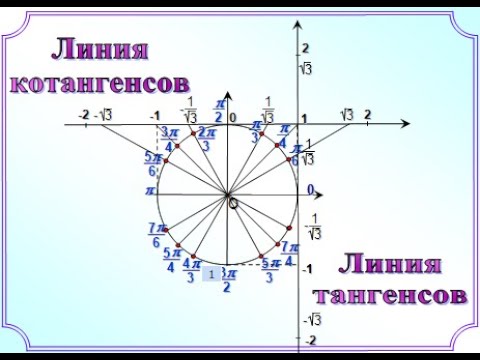
Где же на тригонометрическом круге оси тангенсов и котангенсов?

Ось тангенсов параллельна оси синусов (имеет тоже направление, что ось синусов) и проходит через точку (1; 0).

Ось котангенсов параллельна оси косинусов (имеет тоже направление, что ось косинусов) и проходит через точку (0; 1).

На каждой из осей располагается вот такая цепочка основных значений тангенса и котангенса: Почему так?

Я думаю, вы легко сообразите и сами. 🙂 Можно по-разному рассуждать. Можете, например, использовать тот факт, что и

Собственно, картинка за себя сама говорит.

Если не очень все же понятно, разберем примеры:

Пример 1.

Вычислить

Находим на круге . Эту точку соединяем с точкой (0;0) лучом (начало – точка (0;0)) и смотрим, где этот луч пересекает ось тангенсов. Видим, что

Ответ:

Пример 2.

Вычислить

Находим на круге . Точку (0;0) соединяем с указанной точкой лучом. И видим, что луч никогда не пересечет ось тангенсов.

не существует.

Ответ: не существует

Пример 3.

Вычислить

Находим на круге точку (это та же точка, что и ) и от нее по часовой стрелке (знак минус!) откладываем (). Куда попадаем? Мы окажемся в точке, что на круге у нас (см. рис.) названа как . Эту точку соединяем с точкой (0;0) лучом. Вышли на ось тангенсов в значение .

Так значит,

Ответ:

Пример 4.

Вычислить

Поэтому от точки (именно там будет ) откладываем против часовой стрелки .

Выходим на ось котангенсов, получаем, что

Ответ:

Пример 5.

Вычислить

Находим на круге . Эту точку соединяем с точкой (0; 0). Выходим на ось котангенсов. Видим, что

Ответ:

Теперь, умея находить по тригонометрическому кругу значения тригонометрических функций (а я надеюсь, что статья, где мы начинали знакомство с кругом и учились вычислять значения синусов и косинусов, вами прочитана…), вы можете пройт и тест по теме «Нахождение значений косинуса, синуса, тангенса и котангенса различных углов».

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Таблицы значений синусов, косинусов, тангенсов, котангенсов (sin, cos, tg, ctg)

Таблицы значений синусов (sin), косинусов (cos), тангенсов (tg), котангенсов (ctg) — это мощный и полезный инструмент, помогающий решать множество задач, как теоретического, так и прикладного характера. В этой статье мы приведем таблицу основных тригонометрических функций (синусов, косинусов, тангенсов и котангенсов) для углов 0, 30, 45, 60, 90, . 360 градусов ( 0 , π 6 , π 3 , π 2 , . . . , 2 π радиан). Также будут показаны отдельные таблицы Брадиса для синусов и косинусов, тангенсов и котангенсов с пояснением, как их использовать для нахождения значений основных тригонометрических функций.

Таблица основных тригонометрических функций для углов 0, 30, 45, 60, 90, . 360 градусов

Исходя из определений синуса, косинуса, тангенса и котангенса можно найти значения этих функций для углов 0 и 90 градусов

sin 0 = 0 , cos 0 = 1 , t g 0 = 0 , котангенс нуля — не определен,

sin 90 ° = 1 , cos 90 ° = 0 , с t g 90 ° = 0 , тангенс дявяноста градусов не определен.

Значения синусов, косинусов, тангенсов и котангенсов в курсе геометрии определяются как соотношения сторон прямоугольного треугольника, углы которого равны 30, 60 и 90 градусов, и также 45, 45 и 90 градусов.

Определение тригонометрических функуций для острого угла в прямоугольном треугольнике

Синус — отношение противолежащего катета к гипотенузе.

Косинус — отношение прилежащего катета к гипотенузе.

Тангенс — отношение противолежащего катета к прилежащему.

Котангенс — отношение прилежащего катета к противолежащему.

В соответствии с определениями находятся значения функций:

sin 30 ° = 1 2 , cos 30 ° = 3 2 , t g 30 ° = 3 3 , c t g 30 ° = 3 , sin 45 ° = 2 2 , cos 45 ° = 2 2 , t g 45 ° = 1 , c t g 45 ° = 1 , sin 60 ° = 3 2 , cos 45 ° = 1 2 , t g 45 ° = 3 , c t g 45 ° = 3 3 .

Сведем эти значения в таблицу и назовем ее таблицей основных значений синуса, косинуса, тангенса и котангенса.

Таблица основных значений синусов, косинусов, тангенсов и котангенсов

α °030456090sin α01 22 23 21cos α13 22 21 20t g α03 313н е о п р е д е л е нc t g αн е о п р е д е л е н313 30α , р а д и а н0π 6π 4π 3π 2

Одно из важных свойств тригонометрических функций — периодичность. На основе этого свойства данную таблицу можно расширить,используя формулы приведения. Ниже представим расширенную таблицу значений основных тригонометрических функций для углов 0, 30, 60, . ,120, 135, 150, 180, . , 360 градусов ( 0 , π 6 , π 3 , π 2 , . . . , 2 π радиан).

Таблица синусов, косинусов, тангенсов и котангенсов

α °030456090120135150180210225240270300315330360sin α01 22 23 213 22 21 20— 1 2— 2 2— 3 2— 1— 3 2— 2 2— 1 20cos α13 22 21 20— 1 2— 2 2— 3 2— 1— 3 2— 2 2— 1 201 22 23 21t g α03 313—— 1— 3 3003 313—— 3— 10c t g α—313 30— 3 3— 1— 3—313 30— 3 3— 1— 3—α , р а д и а н0π 6π 4π 3π 22 π 33 π 45 π 6π7 π 65 π 44 π 33 π 25 π 37 π 411 π 62 π

Периодичность синуса, косинуса, тангенса и котангенса позволяет расширять эту таблицу до сколь угодно больших значений углов. Значения, собранные в таблице, используются при решении задач чаще всего, поэтому их рекомендуется выучить наизусть.

Как пользоваться таблицей основных значений тригонометрических функций

Принцип пользования таблицей значений синусов, косинусов, тангенсов и котангенсов понятен на интуитивном уровне. Пересечение строки и столбца дает значение функции для конкретного угла.

Пример. Как пользоваться таблицей синусов, косинусов, тангенсов и котангенсов

Нужно узнать, чему равен sin 7 π 6

Находим в таблице столбец, значение последней ячейки которого равно 7 π 6 радиан — то же самое, что 210 градусов. Затем выбираем сроку таблицы, в которой представлены значения синусов. На пересечении строки и столбца находим искомое значение:

sin 7 π 6 = — 1 2

Таблицы Брадиса

Таблица Брадиса позволяет вычислить значение синуса, косинуса, тангенса или котангенса с точностью до 4-х знаков после запятой без использования вычислительной техники. Это своего рода замена инженерному калькулятору.

Владимир Модестович Брадис (1890 — 1975) — советский математик-педагог, с 1954 года член-корреспондент АПН СССР. Таблицы четырёхзначных логарифмов и натуральных тригонометрических величин, разработанные Брадисом, впервые вышли в 1921 году.

Сначала приведем таблицу Брадиса для синусов и косинусов. Она позволяет достаточно точно вычислять приближенные значения этих функций для углов, содержащих целое количество градусов и минут. В крайнем левом столбце таблицы представлены градусы, а в верхней строке — минуты. Отметим, что все значения углов таблицы Брадиса кратны шести минутам.

Таблица Брадиса для синусов и косинусов

sin	0′	6′	12′	18′	24′	30′	36′	42′	48′	54′	60′	cos	1′	2′	3′
0.0000	90°
0°	0.0000	0017	0035	0052	0070	0087	0105	0122	0140	0157	0175	89°	3	6	9
1°	0175	0192	0209	0227	0244	0262	0279	0297	0314	0332	0349	88°	3	6	9
2°	0349	0366	0384	0401	0419	0436	0454	0471	0488	0506	0523	87°	3	6	9
3°	0523	0541	0558	0576	0593	0610	0628	0645	0663	0680	0698	86°	3	6	9
4°	0698	0715	0732	0750	0767	0785	0802	0819	0837	0854	0.0872	85°	3	6	9
5°	0.0872	0889	0906	0924	0941	0958	0976	0993	1011	1028	1045	84°	3	6	9
6°	1045	1063	1080	1097	1115	1132	1149	1167	1184	1201	1219	83°	3	6	9
7°	1219	1236	1253	1271	1288	1305	1323	1340	1357	1374	1392	82°	3	6	9
8°	1392	1409	1426	1444	1461	1478	1495	1513	1530	1547	1564	81°	3	6	9
9°	1564	1582	1599	1616	1633	1650	1668	1685	1702	1719	0.1736	80°	3	6	9
10°	0.1736	1754	1771	1788	1805	1822	1840	1857	1874	1891	1908	79°	3	6	9
11°	1908	1925	1942	1959	1977	1994	2011	2028	2045	2062	2079	78°	3	6	9
12°	2079	2096	2113	2130	2147	2164	2181	2198	2215	2233	2250	77°	3	6	9
13°	2250	2267	2284	2300	2317	2334	2351	2368	2385	2402	2419	76°	3	6	8
14°	2419	2436	2453	2470	2487	2504	2521	2538	2554	2571	0.2588	75°	3	6	8
15°	0.2588	2605	2622	2639	2656	2672	2689	2706	2723	2740	2756	74°	3	6	8
16°	2756	2773	2790	2807	2823	2840	2857	2874	2890	2907	2924	73°	3	6	8
17°	2924	2940	2957	2974	2990	3007	3024	3040	3057	3074	3090	72°	3	6	8
18°	3090	3107	3123	3140	3156	3173	3190	3206	3223	3239	3256	71°	3	6	8
19°	3256	3272	3289	3305	3322	3338	3355	3371	3387	3404	0.3420	70°	3	5	8
20°	0.3420	3437	3453	3469	3486	3502	3518	3535	3551	3567	3584	69°	3	5	8
21°	3584	3600	3616	3633	3649	3665	3681	3697	3714	3730	3746	68°	3	5	8
22°	3746	3762	3778	3795	3811	3827	3843	3859	3875	3891	3907	67°	3	5	8
23°	3907	3923	3939	3955	3971	3987	4003	4019	4035	4051	4067	66°	3	5	8
24°	4067	4083	4099	4115	4131	4147	4163	4179	4195	4210	0.4226	65°	3	5	8
25°	0.4226	4242	4258	4274	4289	4305	4321	4337	4352	4368	4384	64°	3	5	8
26°	4384	4399	4415	4431	4446	4462	4478	4493	4509	4524	4540	63°	3	5	8
27°	4540	4555	4571	4586	4602	4617	4633	4648	4664	4679	4695	62°	3	5	8
28°	4695	4710	4726	4741	4756	4772	4787	4802	4818	4833	4848	61°	3	5	8
29°	4848	4863	4879	4894	4909	4924	4939	4955	4970	4985	0.5000	60°	3	5	8
30°	0.5000	5015	5030	5045	5060	5075	5090	5105	5120	5135	5150	59°	3	5	8
31°	5150	5165	5180	5195	5210	5225	5240	5255	5270	5284	5299	58°	2	5	7
32°	5299	5314	5329	5344	5358	5373	5388	5402	5417	5432	5446	57°	2	5	7
33°	5446	5461	5476	5490	5505	5519	5534	5548	5563	5577	5592	56°	2	5	7
34°	5592	5606	5621	5635	5650	5664	5678	5693	5707	5721	0.5736	55°	2	5	7
35°	0.5736	5750	5764	5779	5793	5807	5821	5835	5850	5864	0.5878	54°	2	5	7
36°	5878	5892	5906	5920	5934	5948	5962	5976	5990	6004	6018	53°	2	5	7
37°	6018	6032	6046	6060	6074	6088	6101	6115	6129	6143	6157	52°	2	5	7
38°	6157	6170	6184	6198	6211	6225	6239	6252	6266	6280	6293	51°	2	5	7
39°	6293	6307	6320	6334	6347	6361	6374	6388	6401	6414	0.6428	50°	2	4	7
40°	0.6428	6441	6455	6468	6481	6494	6508	6521	6534	6547	6561	49°	2	4	7
41°	6561	6574	6587	6600	6613	6626	6639	6652	6665	6678	6691	48°	2	4	7
42°	6691	6704	6717	6730	6743	6756	6769	6782	6794	6807	6820	47°	2	4	6
43°	6820	6833	6845	6858	6871	6884	6896	8909	6921	6934	6947	46°	2	4	6
44°	6947	6959	6972	6984	6997	7009	7022	7034	7046	7059	0.7071	45°	2	4	6
45°	0.7071	7083	7096	7108	7120	7133	7145	7157	7169	7181	7193	44°	2	4	6
46°	7193	7206	7218	7230	7242	7254	7266	7278	7290	7302	7314	43°	2	4	6
47°	7314	7325	7337	7349	7361	7373	7385	7396	7408	7420	7431	42°	2	4	6
48°	7431	7443	7455	7466	7478	7490	7501	7513	7524	7536	7547	41°	2	4	6
49°	7547	7559	7570	7581	7593	7604	7615	7627	7638	7649	0.7660	40°	2	4	6
50°	0.7660	7672	7683	7694	7705	7716	7727	7738	7749	7760	7771	39°	2	4	6
51°	7771	7782	7793	7804	7815	7826	7837	7848	7859	7869	7880	38°	2	4	5
52°	7880	7891	7902	7912	7923	7934	7944	7955	7965	7976	7986	37°	2	4	5
53°	7986	7997	8007	8018	8028	8039	8049	8059	8070	8080	8090	36°	2	3	5
54°	8090	8100	8111	8121	8131	8141	8151	8161	8171	8181	0.8192	35°	2	3	5
55°	0.8192	8202	8211	8221	8231	8241	8251	8261	8271	8281	8290	34°	2	3	5
56°	8290	8300	8310	8320	8329	8339	8348	8358	8368	8377	8387	33°	2	3	5
57°	8387	8396	8406	8415	8425	8434	8443	8453	8462	8471	8480	32°	2	3	5
58°	8480	8490	8499	8508	8517	8526	8536	8545	8554	8563	8572	31°	2	3	5
59°	8572	8581	8590	8599	8607	8616	8625	8634	8643	8652	0.8660	30°	1	3	4
60°	0.8660	8669	8678	8686	8695	8704	8712	8721	8729	8738	8746	29°	1	3	4
61°	8746	8755	8763	8771	8780	8788	8796	8805	8813	8821	8829	28°	1	3	4
62°	8829	8838	8846	8854	8862	8870	8878	8886	8894	8902	8910	27°	1	3	4
63°	8910	8918	8926	8934	8942	8949	8957	8965	8973	8980	8988	26°	1	3	4
64°	8988	8996	9003	9011	9018	9026	9033	9041	9048	9056	0.9063	25°	1	3	4
65°	0.9063	9070	9078	9085	9092	9100	9107	9114	9121	9128	9135	24°	1	2	4
66°	9135	9143	9150	9157	9164	9171	9178	9184	9191	9198	9205	23°	1	2	3
67°	9205	9212	9219	9225	9232	9239	9245	9252	9259	9256	9272	22°	1	2	3
68°	9272	9278	9285	9291	9298	9304	9311	9317	9323	9330	9336	21°	1	2	3
69°	9336	9342	9348	9354	9361	9367	9373	9379	9383	9391	0.9397	20°	1	2	3
70°	9397	9403	9409	9415	9421	9426	9432	9438	9444	9449	0.9455	19°	1	2	3
71°	9455	9461	9466	9472	9478	9483	9489	9494	9500	9505	9511	18°	1	2	3
72°	9511	9516	9521	9527	9532	9537	9542	9548	9553	9558	9563	17°	1	2	3
73°	9563	9568	9573	9578	9583	9588	9593	9598	9603	9608	9613	16°	1	2	2
74°	9613	9617	9622	9627	9632	9636	9641	9646	9650	9655	0.9659	15°	1	2	2
75°	9659	9664	9668	9673	9677	9681	9686	9690	9694	9699	9703	14°	1	1	2
76°	9703	9707	9711	9715	9720	9724	9728	9732	9736	9740	9744	13°	1	1	2
77°	9744	9748	9751	9755	9759	9763	9767	9770	9774	9778	9781	12°	1	1	2
78°	9781	9785	9789	9792	9796	9799	9803	9806	9810	9813	9816	11°	1	1	2
79°	9816	9820	9823	9826	9829	9833	9836	9839	9842	9845	0.9848	10°	1	1	2
80°	0.9848	9851	9854	9857	9860	9863	9866	9869	9871	9874	9877	9°	0	1	1
81°	9877	9880	9882	9885	9888	9890	9893	9895	9898	9900	9903	8°	0	1	1
82°	9903	9905	9907	9910	9912	9914	9917	9919	9921	9923	9925	7°	0	1	1
83°	9925	9928	9930	9932	9934	9936	9938	9940	9942	9943	9945	6°	0	1	1
84°	9945	9947	9949	9951	9952	9954	9956	9957	9959	9960	9962	5°	0	1	1
85°	9962	9963	9965	9966	9968	9969	9971	9972	9973	9974	9976	4°	0	0	1
86°	9976	9977	9978	9979	9980	9981	9982	9983	9984	9985	9986	3°	0	0	0
87°	9986	9987	9988	9989	9990	9990	9991	9992	9993	9993	9994	2°	0	0	0
88°	9994	9995	9995	9996	9996	9997	9997	9997	9998	9998	0.9998	1°	0	0	0
89°	9998	9999	9999	9999	9999	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	0°	0	0	0
90°	1.0000
sin	60′	54′	48′	42′	36′	30′	24′	18′	12′	6′	0′	cos	1′	2′	3′

Для нахождения значений синусов и косинусов углов, не представленных в таблице, необходимо использовать поправки.

Теперь приведем таблицу Брадиса для тангенсов и котангенсов. Она содержит значения тангенсов углов от 0 до 76 градусов, и котангенсов углов от 14 до 90 градусов.

Таблица Брадиса для тангенса и котангенса

tg	0′	6′	12′	18′	24′	30′	36′	42′	48′	54′	60′	ctg	1′	2′	3′
0	90°
0°	0,000	0017	0035	0052	0070	0087	0105	0122	0140	0157	0175	89°	3	6	9
1°	0175	0192	0209	0227	0244	0262	0279	0297	0314	0332	0349	88°	3	6	9
2°	0349	0367	0384	0402	0419	0437	0454	0472	0489	0507	0524	87°	3	6	9
3°	0524	0542	0559	0577	0594	0612	0629	0647	0664	0682	0699	86°	3	6	9
4°	0699	0717	0734	0752	0769	0787	0805	0822	0840	0857	0,0875	85°	3	6	9
5°	0,0875	0892	0910	0928	0945	0963	0981	0998	1016	1033	1051	84°	3	6	9
6°	1051	1069	1086	1104	1122	1139	1157	1175	1192	1210	1228	83°	3	6	9
7°	1228	1246	1263	1281	1299	1317	1334	1352	1370	1388	1405	82°	3	6	9
8°	1405	1423	1441	1459	1477	1495	1512	1530	1548	1566	1584	81°	3	6	9
9°	1584	1602	1620	1638	1655	1673	1691	1709	1727	1745	0,1763	80°	3	6	9
10°	0,1763	1781	1799	1817	1835	1853	1871	1890	1908	1926	1944	79°	3	6	9
11°	1944	1962	1980	1998	2016	2035	2053	2071	2089	2107	2126	78°	3	6	9
12°	2126	2144	2162	2180	2199	2217	2235	2254	2272	2290	2309	77°	3	6	9
13°	2309	2327	2345	2364	2382	2401	2419	2438	2456	2475	2493	76°	3	6	9
14°	2493	2512	2530	2549	2568	2586	2605	2623	2642	2661	0,2679	75°	3	6	9
15°	0,2679	2698	2717	2736	2754	2773	2792	2811	2830	2849	2867	74°	3	6	9
16°	2867	2886	2905	2924	2943	2962	2981	3000	3019	3038	3057	73°	3	6	9
17°	3057	3076	3096	3115	3134	3153	3172	3191	3211	3230	3249	72°	3	6	10
18°	3249	3269	3288	3307	3327	3346	3365	3385	3404	3424	3443	71°	3	6	10
19°	3443	3463	3482	3502	3522	3541	3561	3581	3600	3620	0,3640	70°	3	7	10
20°	0,3640	3659	3679	3699	3719	3739	3759	3779	3799	3819	3839	69°	3	7	10
21°	3839	3859	3879	3899	3919	3939	3959	3979	4000	4020	4040	68°	3	7	10
22°	4040	4061	4081	4101	4122	4142	4163	4183	4204	4224	4245	67°	3	7	10
23°	4245	4265	4286	4307	4327	4348	4369	4390	4411	4431	4452	66°	3	7	10
24°	4452	4473	4494	4515	4536	4557	4578	4599	4621	4642	0,4663	65°	4	7	11
25°	0,4663	4684	4706	4727	4748	4770	4791	4813	4834	4856	4877	64°	4	7	11
26°	4877	4899	4921	4942	4964	4986	5008	5029	5051	5073	5095	63°	4	7	11
27°	5095	5117	5139	5161	5184	5206	5228	5250	5272	5295	5317	62°	4	7	11
28°	5317	5340	5362	5384	5407	5430	5452	5475	5498	5520	5543	61°	4	8	11
29°	5543	5566	5589	5612	5635	5658	5681	5704	5727	5750	0,5774	60°	4	8	12
30°	0,5774	5797	5820	5844	5867	5890	5914	5938	5961	5985	6009	59°	4	8	12
31°	6009	6032	6056	6080	6104	6128	6152	6176	6200	6224	6249	58°	4	8	12
32°	6249	6273	6297	6322	6346	6371	6395	6420	6445	6469	6494	57°	4	8	12
33°	6494	6519	6544	6569	6594	6619	6644	6669	6694	6720	6745	56°	4	8	13
34°	6745	6771	6796	6822	6847	6873	6899	6924	6950	6976	0,7002	55°	4	9	13
35°	0,7002	7028	7054	7080	7107	7133	7159	7186	7212	7239	7265	54°	4	8	13
36°	7265	7292	7319	7346	7373	7400	7427	7454	7481	7508	7536	53°	5	9	14°
37°	7536	7563	7590	7618	7646	7673	7701	7729	7757	7785	7813	52°	5	9	14
38°	7813	7841	7869	7898	7926	7954	7983	8012	8040	8069	8098	51°	5	9	14
39°	8098	8127	8156	8185	8214	8243	8273	8302	8332	8361	0,8391	50°	5	10	15
40°	0,8391	8421	8451	8481	8511	8541	8571	8601	8632	8662	0,8693	49°	5	10	15
41°	8693	8724	8754	8785	8816	8847	8878	8910	8941	8972	9004	48°	5	10	16
42°	9004	9036	9067	9099	9131	9163	9195	9228	9260	9293	9325	47°	6	11	16
43°	9325	9358	9391	9424	9457	9490	9523	9556	9590	9623	0,9657	46°	6	11	17
44°	9657	9691	9725	9759	9793	9827	9861	9896	9930	9965	1,0000	45°	6	11	17
45°	1,0000	0035	0070	0105	0141	0176	0212	0247	0283	0319	0355	44°	6	12	18
46°	0355	0392	0428	0464	0501	0538	0575	0612	0649	0686	0724	43°	6	12	18
47°	0724	0761	0799	0837	0875	0913	0951	0990	1028	1067	1106	42°	6	13	19
48°	1106	1145	1184	1224	1263	1303	1343	1383	1423	1463	1504	41°	7	13	20
49°	1504	1544	1585	1626	1667	1708	1750	1792	1833	1875	1,1918	40°	7	14	21
50°	1,1918	1960	2002	2045	2088	2131	2174	2218	2261	2305	2349	39°	7	14	22
51°	2349	2393	2437	2482	2527	2572	2617	2662	2708	2753	2799	38°	8	15	23
52°	2799	2846	2892	2938	2985	3032	3079	3127	3175	3222	3270	37°	8	16	24
53°	3270	3319	3367	3416	3465	3514	3564	3613	3663	3713	3764	36°	8	16	25
54°	3764	3814	3865	3916	3968	4019	4071	4124	4176	4229	1,4281	35°	9	17	26
55°	1,4281	4335	4388	4442	4496	4550	4605	4659	4715	4770	4826	34°	9	18	27
56°	4826	4882	4938	4994	5051	5108	5166	5224	5282	5340	5399	33°	10	19	29
57°	5399	5458	5517	5577	5637	5697	5757	5818	5880	5941	6003	32°	10	20	30
58°	6003	6066	6128	6191	6255	6319	6383	6447	6512	6577	6643	31°	11	21	32
59°	6643	6709	6775	6842	6909	6977	7045	7113	7182	7251	1,7321	30°	11	23	34
60°	1,732	1,739	1,746	1,753	1,760	1,767	1,775	1,782	1,789	1,797	1,804	29°	1	2	4
61°	1,804	1,811	1,819	1,827	1,834	1,842	1,849	1,857	1,865	1,873	1,881	28°	1	3	4
62°	1,881	1,889	1,897	1,905	1,913	1,921	1,929	1,937	1,946	1,954	1,963	27°	1	3	4
63°	1,963	1,971	1,980	1,988	1,997	2,006	2,014	2,023	2,032	2,041	2,05	26°	1	3	4
64°	2,050	2,059	2,069	2,078	2,087	2,097	2,106	2,116	2,125	2,135	2,145	25°	2	3	5
65°	2,145	2,154	2,164	2,174	2,184	2,194	2,204	2,215	2,225	2,236	2,246	24°	2	3	5
66°	2,246	2,257	2,267	2,278	2,289	2,3	2,311	2,322	2,333	2,344	2,356	23°	2	4	5
67°	2,356	2,367	2,379	2,391	2,402	2,414	2,426	2,438	2,450	2,463	2,475	22°	2	4	6
68°	2,475	2,488	2,5	2,513	2,526	2,539	2,552	2,565	2,578	2,592	2,605	21°	2	4	6
69°	2,605	2,619	2,633	2,646	2,66	2,675	2,689	2,703	2,718	2,733	2,747	20°	2	5	7
70°	2,747	2,762	2,778	2,793	2,808	2,824	2,840	2,856	2,872	2,888	2,904	19°	3	5	8
71°	2,904	2,921	2,937	2,954	2,971	2,989	3,006	3,024	3,042	3,06	3,078	18°	3	6	9
72°	3,078	3,096	3,115	3,133	3,152	3,172	3,191	3,211	3,230	3,251	3,271	17°	3	6	10
73°	3,271	3,291	3,312	3,333	3,354	3,376	3	7	10
3,398	3,42	3,442	3,465	3,487	16°	4	7	11
74°	3,487	3,511	3,534	3,558	3,582	3,606	4	8	12
3,630	3,655	3,681	3,706	3,732	15°	4	8	13
75°	3,732	3,758	3,785	3,812	3,839	3,867	4	9	13
3,895	3,923	3,952	3,981	4,011	14°	5	10	14
tg	60′	54′	48′	42′	36′	30′	24′	18′	12′	6′	0′	ctg	1′	2′	3′

Как пользоваться таблицами Брадиса

Рассмотрим таблицу Брадиса для синусов и косинусов. Все, что относится к синусам находится вверху и слева. Если нам нужны косинусы — смотрим на правую сторону внизу таблицы.

Для нахождения значений синуса угла нужно найти пересечение строки, содержащей в крайней левой ячейке необходимое количество градусов, и столбца, содержащего в верхней ячейке необходимое число минут.

Если точного значения угла нет в таблице Брадиса, прибегаем к помощи поправок. Поправки на одну, две и три минуты даны в крайних правых столбцах таблицы. Для нахождения значения синуса угла, которого нет в таблице, находим самое близкое к нему значение. После этого прибавляем или отнимаем поправку, соответствующую разнице между углами.

В случае, если мы ищем синус угла, который больше 90 градусов, сначала нужно воспользоваться формулами приведения, а уже потом — таблицей Брадиса.

Пример. Как пользоваться таблицей Брадиса

Пусть нужно найти синус угла 17 ° 44 ‘ . По таблице находим, чему равен синус 17 ° 42 ‘ и прибавляем к его значению поправку на две минуты:

17 ° 44 ‘ — 17 ° 42 ‘ = 2 ‘ ( н е о б х о д и м а я п о п р а в к а ) sin 17 ° 44 ‘ = 0 . 3040 + 0 . 0006 = 0 . 3046

Принцип работы с косинусами, тангенсами и котангенсами аналогичен. Однако, важно помнить о знаке поправок.

При вычислении значений синусов поправка имеет положительный знак, а при вычислении косинусов поправку необходимо брать с отрицательным знаком.

Таблица синусов, косинусов, тангенсов, котангенсов

Таблицы Брадиса для sin, cos, tg, ctg.

Таблица синусов, косинусов, тангенсов, котангенсов содержит вычисленные значения тригонометрических функций для определенного угла от 0 до 360 градусов в виде простой таблицы и в виде таблицы Брадиса. Так же приведены значения тригонометрических функций в радианах для наиболее распространённых углов, применяемых при вычислениях.

Таблицы с вычисленными значениями sin, cos, tg, ctg применяются для упрощения и ускорения математических вычислений, когда нет возможности воспользоваться калькулятором или компьютером.

• sin
• cos
• tg
• ctg
• триг. функции
• Брадиса sin и cos
• Брадиса tg и ctg

Таблица синусов от 0°до 360°

sin 0° = sin 360° = 0

α°	sin α	α°	sin α	α°	sin α	α°	sin α

α°	sin α	α°	sin α	α°	sin α	α°	sin α

Таблица косинусов от 0° до 360°

cos 0° = cos 360° = 1

α°	cos α	α°	cos α	α°	cos α	α°	cos α

α°	cos α	α°	cos α	α°	cos α	α°	cos α

Таблица тангенсов от 0° до 360°

tg 0° = tg 360° = 0

α°	tg α	α°	tg α	α°	tg α	α°	tg α

α°	tg α	α°	tg α	α°	tg α	α°	tg α

Таблица котангенсов от 0° до 360°

α°	ctg α	α°	ctg α	α°	ctg α	α°	ctg α

α°	ctg α	α°	ctg α	α°	ctg α	α°	ctg α

Значения тригонометрических функций в радианах для наиболее распространённых углов.

Таблица Брадиса для синусов и косинусов

sin	0′	6′	12′	18′	24′	30′	36′	42′	48′	54′	60′	cos	1′	2′	3′
0.0000	90°
0°	0.0000	0017	0035	0052	0070	0087	0105	0122	0140	0157	0175	89°	3	6	9
1°	0175	0192	0209	0227	0244	0262	0279	0297	0314	0332	0349	88°	3	6	9
2°	0349	0366	0384	0401	0419	0436	0454	0471	0488	0506	0523	87°	3	6	9
3°	0523	0541	0558	0576	0593	0610	0628	0645	0663	0680	0698	86°	3	6	9
4°	0698	0715	0732	0750	0767	0785	0802	0819	0837	0854	0.0872	85°	3	6	9
5°	0.0872	0889	0906	0924	0941	0958	0976	0993	1011	1028	1045	84°	3	6	9
6°	1045	1063	1080	1097	1115	1132	1149	1167	1184	1201	1219	83°	3	6	9
7°	1219	1236	1253	1271	1288	1305	1323	1340	1357	1374	1392	82°	3	6	9
8°	1392	1409	1426	1444	1461	1478	1495	1513	1530	1547	1564	81°	3	6	9
9°	1564	1582	1599	1616	1633	1650	1668	1685	1702	1719	0.1736	80°	3	6	9
10°	0.1736	1754	1771	1788	1805	1822	1840	1857	1874	1891	1908	79°	3	6	9
11°	1908	1925	1942	1959	1977	1994	2011	2028	2045	2062	2079	78°	3	6	9
12°	2079	2096	2113	2130	2147	2164	2181	2198	2215	2233	2250	77°	3	6	9
13°	2250	2267	2284	2300	2317	2334	2351	2368	2385	2402	2419	76°	3	6	8
14°	2419	2436	2453	2470	2487	2504	2521	2538	2554	2571	0.2588	75°	3	6	8
15°	0.2588	2605	2622	2639	2656	2672	2689	2706	2723	2740	2756	74°	3	6	8
16°	2756	2773	2790	2807	2823	2840	2857	2874	2890	2907	2924	73°	3	6	8
17°	2924	2940	2957	2974	2990	3007	3024	3040	3057	3074	3090	72°	3	6	8
18°	3090	3107	3123	3140	3156	3173	3190	3206	3223	3239	3256	71°	3	6	8
19°	3256	3272	3289	3305	3322	3338	3355	3371	3387	3404	0.3420	70°	3	5	8
20°	0.3420	3437	3453	3469	3486	3502	3518	3535	3551	3567	3584	69°	3	5	8
21°	3584	3600	3616	3633	3649	3665	3681	3697	3714	3730	3746	68°	3	5	8
22°	3746	3762	3778	3795	3811	3827	3843	3859	3875	3891	3907	67°	3	5	8
23°	3907	3923	3939	3955	3971	3987	4003	4019	4035	4051	4067	66°	3	5	8
24°	4067	4083	4099	4115	4131	4147	4163	4179	4195	4210	0.4226	65°	3	5	8
25°	0.4226	4242	4258	4274	4289	4305	4321	4337	4352	4368	4384	64°	3	5	8
26°	4384	4399	4415	4431	4446	4462	4478	4493	4509	4524	4540	63°	3	5	8
27°	4540	4555	4571	4586	4602	4617	4633	4648	4664	4679	4695	62°	3	5	8
28°	4695	4710	4726	4741	4756	4772	4787	4802	4818	4833	4848	61°	3	5	8
29°	4848	4863	4879	4894	4909	4924	4939	4955	4970	4985	0.5000	60°	3	5	8
30°	0.5000	5015	5030	5045	5060	5075	5090	5105	5120	5135	5150	59°	3	5	8
31°	5150	5165	5180	5195	5210	5225	5240	5255	5270	5284	5299	58°	2	5	7
32°	5299	5314	5329	5344	5358	5373	5388	5402	5417	5432	5446	57°	2	5	7
33°	5446	5461	5476	5490	5505	5519	5534	5548	5563	5577	5592	56°	2	5	7
34°	5592	5606	5621	5635	5650	5664	5678	5693	5707	5721	0.5736	55°	2	5	7
35°	0.5736	5750	5764	5779	5793	5807	5821	5835	5850	5864	0.5878	54°	2	5	7
36°	5878	5892	5906	5920	5934	5948	5962	5976	5990	6004	6018	53°	2	5	7
37°	6018	6032	6046	6060	6074	6088	6101	6115	6129	6143	6157	52°	2	5	7
38°	6157	6170	6184	6198	6211	6225	6239	6252	6266	6280	6293	51°	2	5	7
39°	6293	6307	6320	6334	6347	6361	6374	6388	6401	6414	0.6428	50°	2	4	7
40°	0.6428	6441	6455	6468	6481	6494	6508	6521	6534	6547	6561	49°	2	4	7
41°	6561	6574	6587	6600	6613	6626	6639	6652	6665	6678	6691	48°	2	4	7
42°	6691	6704	6717	6730	6743	6756	6769	6782	6794	6807	6820	47°	2	4	6
43°	6820	6833	6845	6858	6871	6884	6896	8909	6921	6934	6947	46°	2	4	6
44°	6947	6959	6972	6984	6997	7009	7022	7034	7046	7059	0.7071	45°	2	4	6
45°	0.7071	7083	7096	7108	7120	7133	7145	7157	7169	7181	7193	44°	2	4	6
46°	7193	7206	7218	7230	7242	7254	7266	7278	7290	7302	7314	43°	2	4	6
47°	7314	7325	7337	7349	7361	7373	7385	7396	7408	7420	7431	42°	2	4	6
48°	7431	7443	7455	7466	7478	7490	7501	7513	7524	7536	7547	41°	2	4	6
49°	7547	7559	7570	7581	7593	7604	7615	7627	7638	7649	0.7660	40°	2	4	6
50°	0.7660	7672	7683	7694	7705	7716	7727	7738	7749	7760	7771	39°	2	4	6
51°	7771	7782	7793	7804	7815	7826	7837	7848	7859	7869	7880	38°	2	4	5
52°	7880	7891	7902	7912	7923	7934	7944	7955	7965	7976	7986	37°	2	4	5
53°	7986	7997	8007	8018	8028	8039	8049	8059	8070	8080	8090	36°	2	3	5
54°	8090	8100	8111	8121	8131	8141	8151	8161	8171	8181	0.8192	35°	2	3	5
55°	0.8192	8202	8211	8221	8231	8241	8251	8261	8271	8281	8290	34°	2	3	5
56°	8290	8300	8310	8320	8329	8339	8348	8358	8368	8377	8387	33°	2	3	5
57°	8387	8396	8406	8415	8425	8434	8443	8453	8462	8471	8480	32°	2	3	5
58°	8480	8490	8499	8508	8517	8526	8536	8545	8554	8563	8572	31°	2	3	5
59°	8572	8581	8590	8599	8607	8616	8625	8634	8643	8652	0.8660	30°	1	3	4
60°	0.8660	8669	8678	8686	8695	8704	8712	8721	8729	8738	8746	29°	1	3	4
61°	8746	8755	8763	8771	8780	8788	8796	8805	8813	8821	8829	28°	1	3	4
62°	8829	8838	8846	8854	8862	8870	8878	8886	8894	8902	8910	27°	1	3	4
63°	8910	8918	8926	8934	8942	8949	8957	8965	8973	8980	8988	26°	1	3	4
64°	8988	8996	9003	9011	9018	9026	9033	9041	9048	9056	0.9063	25°	1	3	4
65°	0.9063	9070	9078	9085	9092	9100	9107	9114	9121	9128	9135	24°	1	2	4
66°	9135	9143	9150	9157	9164	9171	9178	9184	9191	9198	9205	23°	1	2	3
67°	9205	9212	9219	9225	9232	9239	9245	9252	9259	9256	9272	22°	1	2	3
68°	9272	9278	9285	9291	9298	9304	9311	9317	9323	9330	9336	21°	1	2	3
69°	9336	9342	9348	9354	9361	9367	9373	9379	9383	9391	0.9397	20°	1	2	3
70°	9397	9403	9409	9415	9421	9426	9432	9438	9444	9449	0.9455	19°	1	2	3
71°	9455	9461	9466	9472	9478	9483	9489	9494	9500	9505	9511	18°	1	2	3
72°	9511	9516	9521	9527	9532	9537	9542	9548	9553	9558	9563	17°	1	2	3
73°	9563	9568	9573	9578	9583	9588	9593	9598	9603	9608	9613	16°	1	2	2
74°	9613	9617	9622	9627	9632	9636	9641	9646	9650	9655	0.9659	15°	1	2	2
75°	9659	9664	9668	9673	9677	9681	9686	9690	9694	9699	9703	14°	1	1	2
76°	9703	9707	9711	9715	9720	9724	9728	9732	9736	9740	9744	13°	1	1	2
77°	9744	9748	9751	9755	9759	9763	9767	9770	9774	9778	9781	12°	1	1	2
78°	9781	9785	9789	9792	9796	9799	9803	9806	9810	9813	9816	11°	1	1	2
79°	9816	9820	9823	9826	9829	9833	9836	9839	9842	9845	0.9848	10°	1	1	2
80°	0.9848	9851	9854	9857	9860	9863	9866	9869	9871	9874	9877	9°	0	1	1
81°	9877	9880	9882	9885	9888	9890	9893	9895	9898	9900	9903	8°	0	1	1
82°	9903	9905	9907	9910	9912	9914	9917	9919	9921	9923	9925	7°	0	1	1
83°	9925	9928	9930	9932	9934	9936	9938	9940	9942	9943	9945	6°	0	1	1
84°	9945	9947	9949	9951	9952	9954	9956	9957	9959	9960	9962	5°	0	1	1
85°	9962	9963	9965	9966	9968	9969	9971	9972	9973	9974	9976	4°	0	0	1
86°	9976	9977	9978	9979	9980	9981	9982	9983	9984	9985	9986	3°	0	0	0
87°	9986	9987	9988	9989	9990	9990	9991	9992	9993	9993	9994	2°	0	0	0
88°	9994	9995	9995	9996	9996	9997	9997	9997	9998	9998	0.9998	1°	0	0	0
89°	9998	9999	9999	9999	9999	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	0°	0	0	0
90°	1.0000
sin	60′	54′	48′	42′	36′	30′	24′	18′	12′	6′	0′	cos	1′	2′	3′

Таблица Брадиса для тангенсов и котангенсов

tg	0′	6′	12′	18′	24′	30′	36′	42′	48′	54′	60′	ctg	1′	2′	3′
0	90°
0°	0,000	0017	0035	0052	0070	0087	0105	0122	0140	0157	0175	89°	3	6	9
1°	0175	0192	0209	0227	0244	0262	0279	0297	0314	0332	0349	88°	3	6	9
2°	0349	0367	0384	0402	0419	0437	0454	0472	0489	0507	0524	87°	3	6	9
3°	0524	0542	0559	0577	0594	0612	0629	0647	0664	0682	0699	86°	3	6	9
4°	0699	0717	0734	0752	0769	0787	0805	0822	0840	0857	0,0875	85°	3	6	9
5°	0,0875	0892	0910	0928	0945	0963	0981	0998	1016	1033	1051	84°	3	6	9
6°	1051	1069	1086	1104	1122	1139	1157	1175	1192	1210	1228	83°	3	6	9
7°	1228	1246	1263	1281	1299	1317	1334	1352	1370	1388	1405	82°	3	6	9
8°	1405	1423	1441	1459	1477	1495	1512	1530	1548	1566	1584	81°	3	6	9
9°	1584	1602	1620	1638	1655	1673	1691	1709	1727	1745	0,1763	80°	3	6	9
10°	0,1763	1781	1799	1817	1835	1853	1871	1890	1908	1926	1944	79°	3	6	9
11°	1944	1962	1980	1998	2016	2035	2053	2071	2089	2107	2126	78°	3	6	9
12°	2126	2144	2162	2180	2199	2217	2235	2254	2272	2290	2309	77°	3	6	9
13°	2309	2327	2345	2364	2382	2401	2419	2438	2456	2475	2493	76°	3	6	9
14°	2493	2512	2530	2549	2568	2586	2605	2623	2642	2661	0,2679	75°	3	6	9
15°	0,2679	2698	2717	2736	2754	2773	2792	2811	2830	2849	2867	74°	3	6	9
16°	2867	2886	2905	2924	2943	2962	2981	3000	3019	3038	3057	73°	3	6	9
17°	3057	3076	3096	3115	3134	3153	3172	3191	3211	3230	3249	72°	3	6	10
18°	3249	3269	3288	3307	3327	3346	3365	3385	3404	3424	3443	71°	3	6	10
19°	3443	3463	3482	3502	3522	3541	3561	3581	3600	3620	0,3640	70°	3	7	10
20°	0,3640	3659	3679	3699	3719	3739	3759	3779	3799	3819	3839	69°	3	7	10
21°	3839	3859	3879	3899	3919	3939	3959	3979	4000	4020	4040	68°	3	7	10
22°	4040	4061	4081	4101	4122	4142	4163	4183	4204	4224	4245	67°	3	7	10
23°	4245	4265	4286	4307	4327	4348	4369	4390	4411	4431	4452	66°	3	7	10
24°	4452	4473	4494	4515	4536	4557	4578	4599	4621	4642	0,4663	65°	4	7	11
25°	0,4663	4684	4706	4727	4748	4770	4791	4813	4834	4856	4877	64°	4	7	11
26°	4877	4899	4921	4942	4964	4986	5008	5029	5051	5073	5095	63°	4	7	11
27°	5095	5117	5139	5161	5184	5206	5228	5250	5272	5295	5317	62°	4	7	11
28°	5317	5340	5362	5384	5407	5430	5452	5475	5498	5520	5543	61°	4	8	11
29°	5543	5566	5589	5612	5635	5658	5681	5704	5727	5750	0,5774	60°	4	8	12
30°	0,5774	5797	5820	5844	5867	5890	5914	5938	5961	5985	6009	59°	4	8	12
31°	6009	6032	6056	6080	6104	6128	6152	6176	6200	6224	6249	58°	4	8	12
32°	6249	6273	6297	6322	6346	6371	6395	6420	6445	6469	6494	57°	4	8	12
33°	6494	6519	6544	6569	6594	6619	6644	6669	6694	6720	6745	56°	4	8	13
34°	6745	6771	6796	6822	6847	6873	6899	6924	6950	6976	0,7002	55°	4	9	13
35°	0,7002	7028	7054	7080	7107	7133	7159	7186	7212	7239	7265	54°	4	8	13
36°	7265	7292	7319	7346	7373	7400	7427	7454	7481	7508	7536	53°	5	9	14°
37°	7536	7563	7590	7618	7646	7673	7701	7729	7757	7785	7813	52°	5	9	14
38°	7813	7841	7869	7898	7926	7954	7983	8012	8040	8069	8098	51°	5	9	14
39°	8098	8127	8156	8185	8214	8243	8273	8302	8332	8361	0,8391	50°	5	10	15
40°	0,8391	8421	8451	8481	8511	8541	8571	8601	8632	8662	0,8693	49°	5	10	15
41°	8693	8724	8754	8785	8816	8847	8878	8910	8941	8972	9004	48°	5	10	16
42°	9004	9036	9067	9099	9131	9163	9195	9228	9260	9293	9325	47°	6	11	16
43°	9325	9358	9391	9424	9457	9490	9523	9556	9590	9623	0,9657	46°	6	11	17
44°	9657	9691	9725	9759	9793	9827	9861	9896	9930	9965	1,0000	45°	6	11	17
45°	1,0000	0035	0070	0105	0141	0176	0212	0247	0283	0319	0355	44°	6	12	18
46°	0355	0392	0428	0464	0501	0538	0575	0612	0649	0686	0724	43°	6	12	18
47°	0724	0761	0799	0837	0875	0913	0951	0990	1028	1067	1106	42°	6	13	19
48°	1106	1145	1184	1224	1263	1303	1343	1383	1423	1463	1504	41°	7	13	20
49°	1504	1544	1585	1626	1667	1708	1750	1792	1833	1875	1,1918	40°	7	14	21
50°	1,1918	1960	2002	2045	2088	2131	2174	2218	2261	2305	2349	39°	7	14	22
51°	2349	2393	2437	2482	2527	2572	2617	2662	2708	2753	2799	38°	8	15	23
52°	2799	2846	2892	2938	2985	3032	3079	3127	3175	3222	3270	37°	8	16	24
53°	3270	3319	3367	3416	3465	3514	3564	3613	3663	3713	3764	36°	8	16	25
54°	3764	3814	3865	3916	3968	4019	4071	4124	4176	4229	1,4281	35°	9	17	26
55°	1,4281	4335	4388	4442	4496	4550	4605	4659	4715	4770	4826	34°	9	18	27
56°	4826	4882	4938	4994	5051	5108	5166	5224	5282	5340	5399	33°	10	19	29
57°	5399	5458	5517	5577	5637	5697	5757	5818	5880	5941	6003	32°	10	20	30
58°	6003	6066	6128	6191	6255	6319	6383	6447	6512	6577	6643	31°	11	21	32
59°	6643	6709	6775	6842	6909	6977	7045	7113	7182	7251	1,7321	30°	11	23	34
60°	1,732	1,739	1,746	1,753	1,760	1,767	1,775	1,782	1,789	1,797	1,804	29°	1	2	4
61°	1,804	1,811	1,819	1,827	1,834	1,842	1,849	1,857	1,865	1,873	1,881	28°	1	3	4
62°	1,881	1,889	1,897	1,905	1,913	1,921	1,929	1,937	1,946	1,954	1,963	27°	1	3	4
63°	1,963	1,971	1,980	1,988	1,997	2,006	2,014	2,023	2,032	2,041	2,05	26°	1	3	4
64°	2,050	2,059	2,069	2,078	2,087	2,097	2,106	2,116	2,125	2,135	2,145	25°	2	3	5
65°	2,145	2,154	2,164	2,174	2,184	2,194	2,204	2,215	2,225	2,236	2,246	24°	2	3	5
66°	2,246	2,257	2,267	2,278	2,289	2,3	2,311	2,322	2,333	2,344	2,356	23°	2	4	5
67°	2,356	2,367	2,379	2,391	2,402	2,414	2,426	2,438	2,450	2,463	2,475	22°	2	4	6
68°	2,475	2,488	2,5	2,513	2,526	2,539	2,552	2,565	2,578	2,592	2,605	21°	2	4	6
69°	2,605	2,619	2,633	2,646	2,66	2,675	2,689	2,703	2,718	2,733	2,747	20°	2	5	7
70°	2,747	2,762	2,778	2,793	2,808	2,824	2,840	2,856	2,872	2,888	2,904	19°	3	5	8
71°	2,904	2,921	2,937	2,954	2,971	2,989	3,006	3,024	3,042	3,06	3,078	18°	3	6	9
72°	3,078	3,096	3,115	3,133	3,152	3,172	3,191	3,211	3,230	3,251	3,271	17°	3	6	10
73°	3,271	3,291	3,312	3,333	3,354	3,376	3	7	10
3,398	3,42	3,442	3,465	3,487	16°	4	7	11
74°	3,487	3,511	3,534	3,558	3,582	3,606	4	8	12
3,630	3,655	3,681	3,706	3,732	15°	4	8	13
75°	3,732	3,758	3,785	3,812	3,839	3,867	4	9	13
3,895	3,923	3,952	3,981	4,011	14°	5	10	14
tg	60′	54′	48′	42′	36′	30′	24′	18′	12′	6′	0′	ctg	1′	2′	3′

Тригонометрия и тригонометрические функции

Тригонометрия – раздел математики, изучающий зависимости углов и сторон треугольников, которые выражены функциями, называемыми тригонометрическими.

Функция – это правило, описывающее зависимость одной величины от другой.

Угол — это геометрическая фигура, образованная двумя линиями, не лежащими на одной прямой и выходящими или пересекающимися в одной точке.

Углы по своему виду могут быть:

• острыми – меньше 90 градусов
• тупыми – больше 90 градусов
• прямыми – равными 90 градусов (прямые или отрезки перпендикулярны)

Треугольник – это геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Отрезки называют сторонами треугольника, а точки – вершинами треугольника.

В зависимости от соотношения сторон и углов, треугольники можно разделить на группы:

Прямоугольный треугольник

гипотенуза – сторона прямоугольного треугольника, лежащая против прямого угла и являющаяся самой длинной стороной прямоугольного треугольника.

катет – одна из сторон прямоугольного треугольника, образующая прямой угол треугольника. Может называться противолежащим или прилежащим. Противолежащий – это катет, расположенный напротив рассматриваемого угла треугольника, прилежащий – это катет, прилежащий к рассматриваемому углу треугольника.

Чтобы вычислить какой-либо неизвестный элемент (сторону или угол) имеющегося треугольника, зная часть элементов того же треугольника, используют определенные зависимости (правила) между величинами углов и длинами сторон этого треугольника. Такие зависимости называют тригонометрическими функциями.

К базовым тригонометрическим функциям относятся:

То есть, тригонометрические функций позволяют, зная какой-либо угол и сторону, вычислить значения других неизвестных элементов треугольника.

Таблицы с вычисленными значениями синусов, косинусов, тангенсов, котангенсов.

Для ускорения расчетов, когда нет под рукой калькулятора, смартфона или компьютера, раньше были очень популярны таблицы с заранее вычисленными соотношениями сторон треугольников, выраженными в вычисленных значениях sin, cos, tg.

Например, зная из таблицы значения вычисленных заранее тригонометрических функций известного угла треугольника и длину одной из его сторон, можно быстро вычислить длины других сторон треугольника и величины неизвестных углов.

📸 Видео