Сумма векторов ав вс са

Теорема 1 От любой точки ( K ) можно отложить вектор единственный ( overrightarrow ) .

Существование: Имеем два следующих случая:

Здесь получаем, что искомый нами вектор совпадает с вектором ( overrightarrow ) .

Из данного выше построения сразу же будет следовать единственность данного вектора.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Сумма векторов. Сложение векторов. Правило треугольника

Сложение векторов выполняется по правилу треугольника или по правилу параллелограмма.

Суммой нескольких векторов ( vec ) , ( vec ) , ( vec,;ldots ) называется вектор ( vec ) , получающийся в результате последовательного сложения данных векторов.

Такая операция выполняется по правилу многоугольника.

Сумма векторов в координатах
При сложении двух векторов соответствующие координаты складываются.
( vec + vec = left( <+ , + , + > right) )

Отметим несколько свойств сложения двух векторов:

Для произвольного вектора ( overrightarrow ) выполняется равенство

Для произвольных точек ( A, B и C ) справедливо следующее равенство

Замечание Таким способом также можно строить сумму любого числа векторов. Тогда оно будет носить название правила многоугольника.

Видео:Сложение векторов. 9 класс.Скачать

Разность векторов. Вычитание векторов

Разность двух одинаковых векторов равна нулевому вектору :
( vec — vec = vec )

Длина нулевого вектора равна нулю:
( left| vec right| = 0 )

Разность векторов в координатах
При вычитании двух векторов соответствующие координаты также вычитаются.
( vec — vec = left( <- , — , — > right) )

Видео:8 класс, 43 урок, Сумма двух векторовСкачать

Умножение вектора на число

Пусть нам дан вектор ( overrightarrow ) и действительное число ( k ) .

Определение Произведением вектора ( overrightarrow ) на действительное число ( k ) называется вектор ( overrightarrow ) удовлетворяющий следующим условиям:

Длина вектора ( overrightarrow ) равна ( left|overrightarrowright|=left|kright||overrightarrow| ) ;

Векторы ( overrightarrow ) и ( overrightarrow ) сонаправлены, при ( kge 0 ) и противоположно направлены, если ( kle 0 )

Обозначение: ( overrightarrow=koverrightarrow ) .

Видео:Сложение векторов. Правило параллелограмма. 9 класс.Скачать

Сложение и вычитание векторов 9 класс

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Геометрия 9 класс (Урок№2 - Сумма двух векторов. Законы сложения векторов.)Скачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Сложение и вычитание
векторов
Л.С. Атанасян «Геометрия 7-9»

А
В
С
Какая запись является верной?
450
AВ > BC;
AВ > BC
AC = BC ;
AC = BC

Назовите коллинеарные сонаправленные векторы
Назовите коллинеарные противоположнонаправленные векторы
A
B
C
D
N
M
R
E
S
F
H
J
K
L
Z
I
O
P
X
G
Q
V
T
Y
U
Назовите равные векторы

Сложение векторов. Правило треугольника.
a
a
b
b
a +
b
А
В
С
АВ + ВС =
АС
a + 0 = a
!
!
Для любого нулевого вектора справедливо равенство

В1
Докажем, что если при сложении векторов точку А заменить другой точкой А1, то полученный вектор А1С1
будет равен АС. Рассмотрим случай.
a
b
В
b
a
b
a
b
a +
А
С
b
a +
С1
А1
АВВ1А1 – параллелограмм
ВСС1В1 – параллелограмм
АСС1А1 – параллелограмм

= OK
АВ + ВС =
Правило треугольника.
АС
АО + ОР =
АР
MN + NR =
MR
MK + KM =
MM = 0
MK + OM =
OM + MK
= KE
АS + SС =
АС
NM + ML =
NL
RP + PR =
RR = 0
ZK + KZ =
ZZ = 0
DE + KD =
KD + DE =

Правило треугольника.
АС =
АВ + ВС
OB + ВN
ON =
AR + RS
AS =
XK + KH
XH =
MA + AD
MD =
OF + FP
OP =
ON + NВ
OB =
RS + SA
RA =
KH + HX
KX =
AM + MD
AD =
FP + PO
FO =

По правилу треугольника складываются и коллинеарные векторы, хотя при их сложении треугольника и не получается
a
b
a +
b
a
b
a +
b

Законы сложения векторов
Для любых векторов справедливы равенства:
a, b, c
1
2
a + b = b + a
переместительный закон
сочетательный закон
(a + b) + c = a + (b + c)
!
!
Теорема

Рассмотрим случай, когда векторы и не коллинеарны.
b
a
1

1
2
9
6
12
11
10
8
7
4
5
3
При доказательстве свойства 10 мы обосновали правило параллелограмма сложения неколлинеарных векторов.
Чтобы применить правило параллелограмма, надо отложить векторы от одной точки, как стрелки часов.

Сложение векторов.
Правило многоугольника.
= АO
АВ + ВС + СD + DO
a
c
n
m
c
m
n
a+c+m+n
a

Правило многоугольника можно сформулировать также следующим образом: если А1, А2, …, Аn – произвольные точки плоскости, то
= А1An
А1А2 + А2А3 + … + Аn-1An
А2
А3
А4
А5
А6
А7
А1

!
Если начало первого вектора совпадает с концом последнего вектора, то сумма данных векторов равна нулевому вектору.
a1+a2+a3+a4+a5
= 0
a1
a1
a2
a2
a3
a4
a5
a3
a4
a5

Вектор называется противоположным

вектору , если векторы и имеют равные

длины и противоположно направлены.
a1
b
-b
a
a
a1
-b
b
Вектор , противоположный вектору
А
В
А
В
Вектор ВА, противоположный
вектору АВ
a + (-a) = 0
ВА = – АВ
a
a1
a = a1 ;
a a1

a
b
№ 766 На рисунке изображены векторы

ХУ. Представьте вектор ХУ в виде суммы остальных или им

Вычитание векторов.
MF — SF =
MF + FS
= MS
RO — RM =
RO + MR
= MR + RO
MD — SD =
MD + DS
= MS
— OS — ST =
SO + TS
= TS + SO
RO — AO =
RO + OA
= RA
RO — RO =
RO + OR
= RR
= 0
= TO
= MO

№ 768 Точки М и N – середины сторон АВ и АС

треугольника АВС. Выразите векторы ВМ, NC, MN, BN

( )
Найдите
АВ + AD – DC – OD
ABCD — прямоугольник
А
B
C
D
АВ + AD – DC – OD
= АС – DC – OD
= АС + CD + DO
= АО
О
3
4
5

АВ + ВС =
АО + ОР =
MN + NR =
MK + KM =
MK + OM =
АS + SС =
NM + ML =
RP + PR =
ZK + KZ =
DE + KD =
ON =
AS =
XH =
MD =
OP =
OB =
RA =
KX =
AD =
FO =

Курс повышения квалификации

Охрана труда

• Сейчас обучается 94 человека из 42 регионов

Курс профессиональной переподготовки

Библиотечно-библиографические и информационные знания в педагогическом процессе

• Сейчас обучается 350 человек из 65 регионов

Курс профессиональной переподготовки

Охрана труда

• Сейчас обучается 223 человека из 53 регионов

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 493 028 материалов в базе

Видео:ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Дистанционные курсы для педагогов

Другие материалы

• 03.01.2021
• 219

• 03.01.2021
• 374

• 03.01.2021
• 541

• 03.01.2021
• 379

• 03.01.2021
• 300

• 03.01.2021
• 300

• 03.01.2021
• 403

• 03.01.2021
• 720

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 02.04.2020 1503 —> —> —> —>
• PPTX 2.1 мбайт —> —>
• Рейтинг: 3 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Винокурова Надежда Николаевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 1 год
• Подписчики: 0
• Всего просмотров: 24871
• Всего материалов: 240

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Вычитание векторов. 9 класс.Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В России утвердили новые правила аккредитации образовательных учреждений

Время чтения: 1 минута

Регионы запустили работу по капремонту школ

Время чтения: 1 минута

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

Минпросвещения России запускает конкурс для учителей физкультуры

Время чтения: 2 минуты

Более 800 вузов проведут прием через суперсервис

Время чтения: 1 минута

Школы Сургута переведут на дистанционное обучение с 24 января

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:СУММА ВЕКТОРОВ правило треугольникаСкачать

$ AlexLat $

Одним из фундаментальных понятий современной математики являются вектор и его обобщение — тензор. Эволюция понятия вектора осуществлялась благодаря широкому использованию этого понятия в различных областях математики, механики, а так же в технике.
Конец прошлого и начало текущего столетия ознаменовались широким развитием векторного исчисления и его приложений. Были созданы векторная алгебра и векторный анализ, общая теория векторного пространства. Эти теории были использованы при построении специальной и общей теории относительности, которые играют исключительно важную роль в современной физике.
В соответствии с требованиями новой программы по математике понятие вектора стало одним из ведущих понятий школьного курса математики.
Что же такое вектор? Как ни странно, ответ на этот вопрос представляет известные затруднения. Существуют различные подходы к определению понятия вектора; при этом даже если ограничиться лишь наиболее интересным здесь для нас элементарно-геометрическим подходом к понятию вектора, то и тогда будут иметься различные взгляды на это понятие. Разумеется, какое бы определение мы ни взяли, вектор — с элементарно-геометрической точки зрения — есть геометрический объект, характеризуемый направлением ( т.е. заданной с точностью до параллельности прямой и направлением на ней) и длиной. Однако такое определение является слишком общим, не вызывающим конкретных геометрических представлений. Согласно этому общему определению параллельный перенос можно считать вектором. И действительно, можно было бы принять такое определение: «Вектором называется всякий параллельный перенос». Это определение логически безупречно, и на его основе может быть построена вся теория действий над векторами и развиты приложения этой теории. Однако это определение, несмотря на его полную конкретность , нас здесь также не может удовлетворить, так как представление о векторе как о геометрическом преобразовании кажется нам недостаточно наглядным и далеким от физических представлений о векторных величинах.
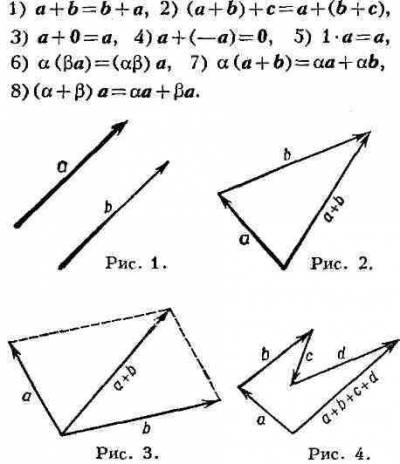
Итак, векторомназывается семейство всех параллельных между собой одинаково направленных и имеющих одинаковую длину отрезков (рис.1). Вектор изображают на чертежах отрезком со стрелкой (т.е. изображают не все семейство отрезков, представляющее собой вектор, а лишь один из этих отрезков). Для обозначения векторов в книгах и статьях применяют жирные латинские буквы а, в, с и так далее, а в тетрадях и на доске — латинские буквы с черточкой сверху,
Той же буквой, но не жирной , а светлой (а в тетради и на доске- той же буквой без черточки) обозначают длину вектора. Длину иногда обозначают также вертикальными черточками — как модуль (абсолютную величину) числа. Таким образом, длина вектора а обозначается через а или IаI, а в рукописном тексте длина вектора а обозначается через а или IаI. В связи с изображением векторов в виде отрезков (рис.2) следует помнить , что концы отрезка, изображающего вектор, неравноправны: одного конца отрезка к другому. Различают начало и конец вектора (точнее, отрезка, изображающего вектор).
Весьма часто понятию вектора дается другое определение: вектором называется направленный отрезок. При этом векторы (т.е. направленные отрезки), имеющие одинаковую длину и одно и то же направление (рис.3), уславливаются считать равными.
Векторы называются одинаково направленными, если их полупрямые одинаково направлены.

Все сказанное пока еще не дает понятие вектора достаточно содержательным и полезным. Большую содержательность и богатую возможность приложений понятие вектора получает тогда, когда мы вводим своеобразную «геометрическую арифметику» — арифметику векторов, позволяющую складывать векторы, вычитать их и производить над ними целый ряд других операций. Отметим в связи с этим, что ведь и понятие числа становится интересным лишь при введении арифметических действий, а не само по себе.
Суммой векторов а и в с координатами а1, а2 и в1, в2 называется вектор с с координатами а1 + в1, а2 + в2 , т.е.
а (а1; а2) + в (в1;в2) = с (а1 + в1; а2 + в2) .
Следствие:
а + в = в + а , (коммутативность)
а + ( в + с ) = (а + в) + с. (ассоциативность)
Для доказательства коммутативности сложения векторов на плоскости необходимо рассмотреть пример.
а и в — векторы (рис.5).
Пусть ОА =а, ОВ = в .
1. Строим параллелограмм ОАСВ: АМ II ОВ, ВН II ОА .

2. а = ОА = ВС ,
в = ОВ = АС , т.к. параллелограмм.
3. ОА + АС = ОВ + ВС = ОС , значит а + в = в + а . ч.т.д.
Для доказательства ассоциативности мы отложим от произвольной точки О вектор ОА = а , от точки А вектор АВ = в и от точки в — вектор ВС = с . Тогда мы имеем: АВ + ВС =АС .
(а + в ) + с = (ОА + АВ) + ВС = ОВ + ВС = ОС,
а + (в + с ) = ОА + (АВ + ВС) = ОА + АС = ОС ,
откуда и следует равенство а + ( в + с ) = (а + в) + с . Заметим, что приведенное доказательство совсем не использует чертежа. Это характерно ( при некотором навыке ) для решения задач при помощи векторов.
Остановимся теперь на случае, когда векторы а и в направлены в противоположные стороны и имеют равные длины; такие векторы называют противоположными. Наше правило сложения векторов приводит к тому, что сумма двух противоположных векторов представляет собой «вектор», имеющий нулевую длину и не имеющий никакого направления; этот «вектор» изображается «отрезком нулевой длины», т.е. точкой. Но это тоже вектор, который называется нулевым и обозначается символом 0 .

Два вектора называются равными, если они совмещаются параллельным переносом. Это означает, что существует параллельный перенос, который переводит начало и конец одного вектора соответственно в начало и конец другого вектора.
Из данного определения равенства векторов следует, что разные векторы одинаково направлены и равны по абсолютной величине.
И обратно: если векторы одинаково направлены и равны по абсолютной величине, то они равны.
Действительно, пусть векторы АВ и СD — одинаково направленные векторы, равные по абсолютной величине (рис.6). Параллельный перенос, переводящий точку С в точку А , совмещает полупрямую СD с полупрямой АВ , так как они одинаково направлены. А так как отрезки АВ и CD равны, то при этом точка D совмещается с точкой В, то есть параллельный перенос переводит вектор CD в вектор АВ . Значит, векторы АВ и СD равны, что и требовалось доказать.

Скалярное произведение двух векторов и его свойства.

Скалярным произведением двух нулевых векторов называется число, равное произведению числовых значений длин этих векторов на косинус угла между векторами.
Обозначение: а х в = IaI * IbI * cos ( а, в).
Свойства скалярного произведения:
1. а х в = в х а .
2. Для того, чтобы два нулевых вектора а и в были перпендикулярны, необходимо и достаточно, чтобы скалярное произведение этих векторов было равно нулю, т.е. а х в = 0 .
3. Выражение а х а будем обозначать а2 и называть скалярным квадратом вектора а .

Свойства операций над векторами.

Имеют место следующие теоремы об операциях над векторами, заданными в координатной форме.
1. Пусть даны а = (ах, аy, аz) и в = ( вx, ву, вz) , тогда сумма этих векторов есть вектор с, координаты которого равны сумме одноименных координат слагаемых векторов, т.е. с = а + в = (ах + вx; аy + ву; аz + вz) .
Пример 1.
а = ( 3; 4; 6) и в = ( -1; 4; -3), тогда с = ( 3 + ( -1); 4 + 4; 6 + (-3)) = ( 2; 8; 3) .
2. а = (ах, аy, аz) и в = ( вx, ву, вz) , тогда разность этих векторов есть вектор с , координаты которого равны разности одноименных координат данных векторов, т.е. с = а — в = (ах — вx; аy — ву; аz — вz) .
Пример 2.
а = ( -2; 8; -3) и в = ( -4; -5; 0), тогда с = а — в = ( -2 — ( -4 ); 8 — ( -5 ); -3 -0 ) = = ( 2; -13; -3) .
3. При умножении вектора а = (ах, аy, аz) на число м все его координаты умножаются на это число, т.е. ма = ( мах, маy, маz).
Пример 3.
а = ( -8; 4; 0) и м = 3 , тогда 3а = ( -8 х 3; 4 х 3; 0 х 3) = ( -24; 12; 0) .
Понятие вектора, которое нашло широкое распространение в прикладных науках, явилось плодотворным и в геометрии. Аппарат векторной алгебры позволил упростить изложение некоторых сложных геометрических понятий, доказательства некоторых теорем школьного курса геометрии, позволил создать особый метод решения различных геометрических задач.
Рассмотрим доказательство некоторых теорем с помощью векторов.
Теорема 1.
Диагонали ромба взаимно перпендикулярны.
Доказательство.
Пусть АВСD — данный ромб (рис.7). Введем обозначения: АВ = а, ВС = в . Из определения ромба: АВ = DC = а, AD = ВС = в .
По определению суммы и разности векторов АС = а + в; DВ = а — в .
Рассмотрим АС * DВ = (а + в )( а — в) = а2 — в2 .
Так как стороны ромба равны, то а = в . Следовательно, AC * DB =0 . Из последнего получаем АС DВ , т.е. DB АС . Ч.т.д.
Рассмотрим теперь решение задач с помощью векторов.
Задача 1.
Даны два вектора AB и CD , причем А( -1; 2; 4) , В ( -4; 5; 4) , С( -1; -2; 2) и D(2; 1;5) .
Определить, перпендикулярны они друг другу или нет.
Решение.
Найдем сначала координаты векторов. АВ = ( -3; 3; 0) и СD = (3; 3; 3) .
Вычислим теперь скалярное произведение этих векторов:
АВ х СD = ( -3) х 3 + 3 х 3 + 0 х 3 = 0 .
Последнее и означает, что АВ СD .

Задача 2.
Дан произвольный треугольник АВС . Доказать, что можно построить треугольник, стороны которого равны и параллельны медианам треугольника АВС .

Решение.
Обозначим медианы треугольника АВС через ВЕ , СF и обозначим векторы, идущие вдоль сторон треугольника АВС , через а, в, с:
ВС = а, СА = в, АВ = с
(рис.8). Тогда
АD = АВ + ВD = АВ += с +
аналогично определяются и другие медианы:
ВЕ = а + , СF = в +
Так как, в силу условия замкнутости
ВС + СА + АВ = а + в + с =0,
то мы имеем:
АD + ВЕ + СF = ( с + ) + (а + ) + ( в + ) = ( а + в + с) = х 0 = 0.
Следовательно, отложив от точки В , вектор В1С1 = ВЕ и от точки С1 — вектор С1D1 = СF , мы получим.
А1В1 + В1С1 + С1D1 = АD + ВЕ + СF = 0.
А это значит (в силу условия замкнутости), что ломаная А1В1С1D1 является замкнутой, т.е. точка D1 совпадает с А1.
Таким образом, мы получаем треугольник А1В1С1 (рис.9), стороны которого равны и параллельны медианам АD, ВЕ, СF исходного треугольника.
Задача 3.
Доказать, что для любого треугольника имеет место формула
с2 = а2 + в2 — 2 ав х соs С (теорема косинусов)

Решение.
Положим: а = СВ, в = СА,
с = АВ (рис.10).
Тогда с = а — в , и мы имеем
(учитывая, что угол между векторами а и в равен С) :

с2 = ( а — в )2 = а2 — 2ав + в2 = а2 — 2ав х соs С + в2 .
Задача 4.
Докажите, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.

Решение.
Пусть четырехугольник АВСD — параллелограмм (рис.11). Имеем векторные равенства
АВ + AD = АС, АВ — АD = DВ.
Возведем эти равенства в квадрат. Получим:
АВ2 + 2 АВ х АD + АD2 = АС2, АВ2 — 2АВ х АD + АD2 = DВ2
Сложим эти равенства почленно. Получим:
2АВ2 + 2 АD2 = АС2 + DВ2.
Так как у параллелограмма противолежащие стороны равны, то это равенство и означает, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон, что и требовалось доказать.

Задача 5.
Даны три точки: А ( 1; 1), В ( -1; 0), С ( 0; 1) . найдите такую точку D ( х; y) , чтобы векторы АВ и СD были равны.
Решение.
Вектор АВ имеет координаты -2, -1 . Вектор СD имеет координаты х — 0, y -1 . Так как АВ = СD , то х — 0 = -2, y -1 = -1 . Отсюда находим координаты точки D: х = -2, y = 0 .

Задача 6.
Даны два вектора АВ и СD , причем А ( -1; 2; 4), В ( -4; 5; 4), С ( -1; -2; 2), D ( 2; 1; 5) .Определить, перпендикулярны они друг другу или нет.
Решение.
Найдем сначала координаты векторов. АВ = ( -3; 3; 0) и СD ( 3; 3; 3) .
Вычислим теперь скалярное произведение этих векторов:
AB х CD = ( -3) х 3 + 3 х 3 + 0 х 3 = 0.
Последнее озночает, что АВ СD .

🔥 Видео

ПРОСТОЙ СПОСОБ, как запомнить Векторы за 10 минут! (вы будете в шоке)Скачать

ВЕКТОРЫ 9 класс С НУЛЯ | Математика ОГЭ 2023 | УмскулСкачать

сложение ВЕКТОРОВ вычитание ВЕКТОРОВ 9 класс геометрия АтанасянСкачать

10 класс, 40 урок, Сложение и вычитание векторовСкачать

Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Сложение и вычитание векторов. Практическая часть. 11 класс.Скачать

Сумма и разность векторов. Урок 2. Геометрия 9 классСкачать

Скалярное произведение векторов. 9 класс.Скачать

Сложение векторов. Практическая часть. 9 класс.Скачать

Сумма двух векторов | Геометрия 7-9 класс #79 | ИнфоурокСкачать

10 класс, 41 урок, Сумма нескольких векторовСкачать