В этой статье мы рассмотрим все основные свойства и признаки четырехугольников.
Для начала я расположу все виды четырехугольников в виде такой сводной схемы:
Схема замечательна тем, что четырехугольники, стоящие в каждой строке обладают ВСЕМИ СВОЙСТВАМИ ЧЕТЫРЕХУГОЛЬНИКОВ, РАСПОЛОЖЕННЫХ НАД НИМИ. Поэтому запоминать надо совсем немного.
Трапеция — это четырехугольник, две стороны которого параллельны, а две другие не параллельны. Параллельные стороны называются основаниями трапеции, а не параллельные — боковыми сторонами.
1. В трапеции сумма углов, прилежащих к боковой стороне равна 180°: А+В=180°, C+D=180°
2. Биссектриса любого угла трапеции отсекает на ее основании отрезок, равный боковой стороне: 
3. Биссектрисы смежных углов трапеции пересекаются под прямым углом.
4.Трапеция называется равнобедренной, если ее боковые стороны равны:
В равнобедренной трапеции
- углы при основании равны,
- проекции боковых сторон на основание равны:
.
.5. Площадь трапеции равна произведению полусуммы оснований на высоту:
Параллелограм — это четырехугольник, у которого противоположные стороны попарно параллельны: 
В параллелограмме:
- противоположные стороны и противоположные углы равны
- диагонали параллелограмма делятся точкой пересечения пополам:
Соответственно, если четырехугольник обладает этими свойствами, то он является параллелограммом.
Площадь параллелограмма равна произведению основания на высоту:
или произведению сторон на синус угла между ними:
:
Ромб — это параллелограмм, у которого все стороны равны:
- противоположные углы равны
- диагонали точкой пересечения делятся пополам
- диагонали взаимно перпендикулярны
- диагонали ромба являются биссектрисами углов
Площадь ромба равна половине произведения диагоналей:
или произведению квадрата стороны на синус угла между сторонами:
Прямоугольник — это параллелограмм, у которого все углы прямые:
- Диагонали прямоугольника равны.
- Диагонали точкой пересечения делятся пополам.
Площадь прямоугольника равна произведению его сторон:
.
Квадрат — это прямоугольник, у которого все стороны равны
Квадрат — это ромб, у которого все углы прямые.
Соответственно: квадрат обладает свойствами ромба и прямоугольника:
- все углы равны 90 градусов
- диагонали точкой пересечения делятся пополам
- диагонали взаимно перпендикулярны
- диагонали являются биссектрисами углов
- диагонали равны
Площадь квадрата равна квадрату его стороны.
Площадь квадрата равна половине произведения диагоналей.
И.В. Фельдман, репетитор по математике.
Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать
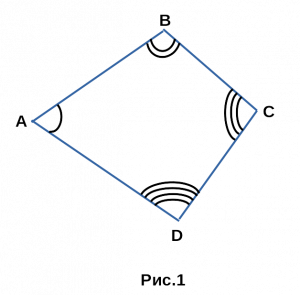
Сумма углов четырехугольника
Свойства
- Сумма углов четырехугольника равна 360°.
∠A + ∠B + ∠C + ∠D = 360°. - Если четырехугольник правильный, то каждый угол по 90°
и этот четырехугольник является квадратом.
∠A = ∠B = ∠C = ∠D, ⇒ ∠A = ∠B = ∠C = ∠D = 90°,
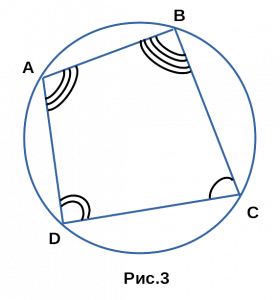
ABCD — квадрат. - Сумма противоположных углов четырехугольника равна 180°,
если около четырехугольника описана окружность.
∠A + ∠С = ∠В + ∠D = 180°.
Такие четырехугольники называют вписанными.
Это все виды четырехугольников,
которые изучаются в школьном
курсе по геометрии.
Видео:Уроки геометрии. Чему равна сумма углов четырехугольника?Скачать
Внутренние односторонние углы
Еще один вид углов, образованных при пересечении двух прямых секущей — внутренние односторонние углы.
Две прямые разбивают плоскость на части. Та часть, которая лежит между прямыми — внутренняя. Углы, которые расположены в этой части, так и называются — внутренние. Внутренние односторонние углы — это углы, которые лежат внутри между прямыми по одну сторону от секущей (поэтому они так и называются).
При пересечении двух прямых секущей образуется две пары внутренних односторонних углов.
∠1 и ∠2
∠3 и ∠4
— внутренние односторонние углы при прямых a и b и секущей c.
Наибольший интерес вызывают внутренние накрест лежащие углы, образованные параллельными прямыми.
Свойство параллельных прямых
Если две параллельные прямые пересечены третьей прямой, то сумма внутренних односторонних углов равна 180º.
Если a ∥ b, то
∠1 + ∠2 = 180º
(как внутренние односторонние при a ∥ b и секущей c).
Признак параллельных прямых
Если сумма внутренних односторонних углов равна 180º, то прямые параллельны.
∠3 + ∠4 =180º
А так как эти углы — внутренние односторонние при a и b и секущей c,
то a ∥ b (по признаку параллельных прямых).
Могут ли быть внутренние односторонние углы равны?
Да. Внутренние односторонние углы равны, если прямые параллельны, а секущая им перпендикулярна.
∠1 и ∠2 — внутренние односторонние углы при прямых a и b и секущей c
∠1 = ∠2
тогда и только тогда, когда a ∥ b, а секущая c перпендикулярна и прямой a, и прямой b.
📽️ Видео
Теорема 14.2 Если сумма односторонних углов равна 180 градусов, то прямые параллельны || Геометрия 7Скачать
Чему равна сумма углов выпуклого многоугольникаСкачать
Параллельные прямые | Математика | TutorOnlineСкачать
7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать
ПОЧЕМУ СУММА УГЛОВ В ТРЕУГОЛЬНИКЕ РАВНА 180? #shorts #геометрия #егэ #огэ #треугольникСкачать
Сумма углов треугольника равна 180Скачать
Геометрия 7 класс (Урок№23 - Сумма углов треугольника.)Скачать
Сумма углов четырехугольника | Математика 8 класс | Четырехугольник | Геометрия 8 классСкачать
Задание 24 Сумма углов четырехугольникаСкачать
Сумма углов любого треугольника равна 180°. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать
№1082. Чему равна сумма внешних углов правильного n-угольника, если при каждой вершинеСкачать
Почему сумма углов любого треугольника 180?Скачать
7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать
Геометрия Докажите что сумма углов четырехугольника равна 360.Скачать
Сумма внутренних углов многоугольника. Выпуклые и невыпуклые многоугольники. 8 класс.Скачать
№429. Докажите, что выпуклый четырехугольник является параллелограммом, если сумма углов, прилежащихСкачать
Красивая задача про углы четырехугольникаСкачать
7 класс. Глава4 - Параллельные прямые. сумма односторонних углов равна 180 градусовСкачать
