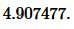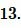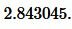Сторона равностороннего треугольника равна Найдите радиус окружности, вписанной в этот треугольник.
Радиус вписанной в треугольник окружности равен отношению площади к полупериметру:
Приведем другое решение.
Центр вписанной окружности находится в точке пересечения биссектрис треугольника. В равностороннем треугольнике биссектрисы являются также медианами и высотами. Пусть биссектриса (она же медиана и высота), проведенная из вершины C, пересекает сторону AB в точке H. Найдем CH из прямоугольного треугольника ACH:
Медианы точкой пересечения делятся в отношении 2:1, следовательно,
- Радиус вписанной окружности в равносторонний треугольник онлайн
- 1. Радиус вписанной в равносторонний треугольник окружности, если известна сторона треугольника
- 2. Радиус вписанной в равносторонний треугольник окружности, если известна высота треугольника
- 3. Радиус вписанной в равносторонний треугольник окружности, если известна площадь треугольника
- Сторона равностороннего треугольника равна 16 3 найдите радиус окружности вписанной
- Как написать хороший ответ?
- 💥 Видео
Видео:Задача 6 №27909 ЕГЭ по математике. Урок 129Скачать

Радиус вписанной окружности в равносторонний треугольник онлайн
С помощю этого онлайн калькулятора можно найти радиус вписанной в любой треугольник окружности, в том числе радиус вписанной в равносторонний треугольник окружности. Для нахождения радиуса вписанной в треугольник окружности выберите тип треугольника, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
| Открыть онлайн калькулятор |
Видео:ОГЭ 2020 задание 17Скачать

1. Радиус вписанной в равносторонний треугольник окружности, если известна сторона треугольника
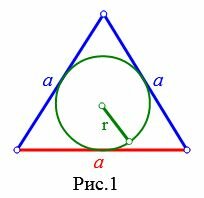
Пусть известна сторона a равностороннего треугольника (Рис.1). Выведем формулу вычисления радиуса вписанной в треугольник окружности.
 |
Радиус вписанной в равнобедренный треугольник окружности через основание a и боковую сторону b вычисляется из следующей формулы:
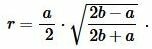 | (1) |
Учитывая, что у равностороннего треугольника все стороны равны (( small a=b )), имеем:
| ( small r=frac cdot sqrt<frac> ) ( small =frac cdot sqrt<frac> ) ( small =frac<large 2 cdot sqrt> ) |
| ( small r=frac<large 2 cdot sqrt> ) | (2) |
или, умножив числитель и знаменатель на ( small sqrt ):
| ( small r=frac<large sqrt> cdot a ) | (3) |
Пример 1. Известна сторона a=17 равностороннего треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся одним из формул (2) и (3). Подставим значения ( small a=17 ) в (3):
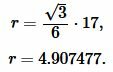 |
Ответ:
Видео:ОГЭ. Задача на описанную окружность № 16. Как легко решить задачуСкачать

2. Радиус вписанной в равносторонний треугольник окружности, если известна высота треугольника
Пусть известна высота h равностороннего треугольника (Рис.2). Выведем формулу радиуса вписанной в треугольник окружности.
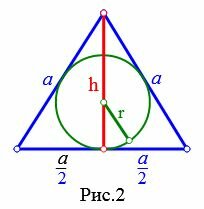 |
Выведем формулу стороны равностороннего треугольника через высоту. Из Теоремы Пифагора имеем:
| ( small h^2+left( frac right) ^2=a^2.) |
| ( small h^2+ frac =a^2; ; ) ( small fraca^2 =h^2; ; ) ( small a^2=frac.) |
| ( small a= frac<large sqrt> .) | (4) |
Формула радиуса вписанной в равнобедренный треугольник окружности по основанию и высоте вычисляется из формулы
| ( small r= large frac<a+sqrt> ) | (5) |
Подставляя (4) в (5), получим:
| ( small r= large frac<frac<large sqrt>><frac<large sqrt>+sqrt<frac+4h^2>> ) ( small = large frac<frac<large sqrt>><frac<large sqrt>+sqrt<frac>> ) ( small = large frac<frac<large sqrt>><frac<large sqrt>+frac<large sqrt>> ) ( small = large fracsmall =large frac small cdot h ) |
То есть, радиус вписанной в равносторонний треугольник окружности по высоте вычисляется из формулы:
| ( small r = large frac small cdot h ) | (6) |
Пример 2. Известна высота ( small h=39 ) равностороннего треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (6). Подставим значение ( small h=39 ) в (6):
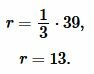 |
Ответ:
Видео:Известна биссектриса равностороннего треугольника. Найти сторону этого треугольника. ОГЭ №16Скачать

3. Радиус вписанной в равносторонний треугольник окружности, если известна площадь треугольника
Пусть известна площадь S равностороннего треугольника (Рис.3). Найдем формулу радиуса вписанной в треугольник окружности.
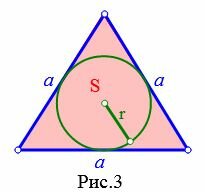 |
Площадь равностороннего треугольника по радиусу вписанной окружности вычисляется из следующей формулы:
| ( small S= 3cdot sqrtr^2.) |
| ( small r^2= large frac |
| ( small r= large frac <sqrt[4]> small cdot sqrt | (7) |
Пример 3. Известна площадь равностороннего треугольника: ( small S=42 . ) Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (7). Подставим значение ( small S=42 ) в (7):
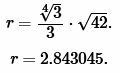 |
Ответ:
Видео:Задание 16 ОГЭ по математике. Окружность описана около равностороннего треугольника. Задача 2Скачать

Сторона равностороннего треугольника равна 16 3 найдите радиус окружности вписанной
Вопрос по математике:
Сторона равностороннего треугольникп равна 16√3. Найдите радиус вписанной в него окружности.
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 1
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Математика.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.
💥 Видео
Задание 16 ОГЭ по математике. Окружность вписана в равносторонний треугольник.Скачать

Шестнадцатое задание ОГЭ по математике (1) #огэ #огэ2023 #огэматематика #огэпоматематике #математикаСкачать

ОГЭ 16🔴Скачать

Геометрия. ОГЭ по математике. Задание 16Скачать

Геометрия. ОГЭ по математике. Задание 16Скачать

Геометрия. ОГЭ по математике. Задание 16Скачать

ЕГЭ профиль #3 / Радиус описанной окружности / Равносторонний треугольник / решу егэСкачать

Радиус окружности, описанной около правильного треугольника, равен 3. Найдите высоту треугольникаСкачать
Задания 16. Тесты 1-5. ОГЭ. Математика.Скачать

ОГЭ ЗАДАНИЕ 16 РАЗДЕЛ ГЕОМЕТРИЯ ПРАВИЛЬНЫЙ ТРЕУГОЛЬНИК И ОКРУЖНОСТЬСкачать

Высота равностороннего треугольника равна 13√3 ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

Геометрия. ОГЭ по математике. Задание 16Скачать

Геометрия Найдите радиус окружности описанной около равнобедренного треугольника с основанием 16 смСкачать

Задача 6 №27921 ЕГЭ по математике. Урок 138Скачать