Ответ:
a — сторона правильного четырех угольника
R — радиус описанной окружности (треугольник вписан, значит окружность описана)
(картинка с сайта https://microexcel.ru/radius-opisannogo-vokrug-kvadrata-kruga/)
Если тебе нужен вывод то вот:
1) Строишь квадрат со стороной а.
2) Вокруг квадрата чертешь описаную окружность с радиусом R.
3) Проводишь диаметры так, чтобы вершина угла квадрата и диаметр пересеклись.
3) диаметры = диагоналям (так как окружность описана) => по свойству параллелограмма: диагонали параллелограмма точкой пересечения делятся пополам => d = 2R
4) Так как квадрат — это ещё и ромб => диагонали параллелограмма при пересечении образуют прямой угол => По теореме Пифагора: a= √(R² + R²)= √(2R²)= R√2
- Тестовая работа по геометрии для 9 класса на тему «Длина окружности и площадь круга»
- Просмотр содержимого документа «Тестовая работа по геометрии для 9 класса на тему «Длина окружности и площадь круга»»
- Презентация по геометрии на тему «Длина окружности и площадь круга» (9 класс)
- Описание презентации по отдельным слайдам:
- 🎬 Видео
Видео:3 правила для вписанного четырехугольника #shortsСкачать

Тестовая работа по геометрии для 9 класса на тему «Длина окружности и площадь круга»
Тематический тест по теме «Длина окружности и площадь круга»
- Четырехугольник является правильным, если:
а)все его углы равны между собой;
б)все его стороны равны между собой;
в)все его углы равны между собой и все его стороны равны между собой.
2. Длина окружности больше диаметра в….
а) 2 раз ; б) раз; в) 2 раза.
3. Длина дуги окружности вычисляется по формуле:
а) l = ; б) l = ; в) l = ;
4. Сторона правильного треугольника, вписанного в окружность с радиусом R, равна:
5. Отношение радиуса вписанной к радиусу описанной около квадрата окружности равно:
6. Отношение радиуса описанной к радиусу вписанной в правильный шестиугольник окружности равно:
7. Каждый угол правильного десятиугольника равен:
а) 140 б) 135 ; в) 144
8. Внешний угол правильного двенадцатиугольника равен:
а) 36 ; б) 30 ; в) 45
9. Из круга, радиус которого равен 20 см, вырезан сектор. Дуга сектора равна 90. Чему равна площадь оставшейся части круга?
а) 100 см2 ; б) 400 см2 ; в) 300 см2 ;
10. Длина дуги окружности с радиусом 12 см и градусной мерой 100 равна:
11. В окружность вписаны квадрат и правильный треугольник. Периметр треугольника равен 30 см, периметр квадрата равен:
Тематический тест по теме «Длина окружности и площадь круга»
- Если в четырехугольнике все стороны равны, то он:
а) всегда является правильным;
б) может быть правильным;
в) никогда не является правильным.
2. Длина окружности больше радиуса в
а) 2 раз ; б) раз; в) 2 раза.
3. Площадь кругового сектора вычисляется по формуле:
а) S = ; б) S = ; в) S = ;
4. Сторона правильного четырехугольника, вписанного в окружность с радиусом R, равна:
5. Отношение радиуса описанной к радиусу вписанной в квадрат окружности равно:
6. Отношение радиуса вписанной к радиусу описанной около правильного шестиугольника окружности равно:
7. Каждый угол правильного восьмиугольника равен:
а) 135 б) 144 ; в) 140 ;
8. Внешний угол правильного двадцатиугольника равен:
а) 20 ; б) 22,5 ; в) 18 ;
9. Из круга, радиус которого равен 30 см, вырезан сектор. Дуга сектора равна 60. Чему равна площадь оставшейся части круга?
а) 150 см2 ; б) 750 см2 ; в) 900 см2 ;
10. Длина дуги окружности с радиусом 6 см и градусной мерой равна 135 равна:
а) см; б) 9 см; в) см ;
11. Площадь круга равна 256. Вычислите длину окружности, радиус которой в два раза больше радиуса круга.
а) 16 ; б) 32 ; в) 64 ;
Тематический тест по теме «Длина окружности и площадь круга»
Просмотр содержимого документа
«Тестовая работа по геометрии для 9 класса на тему «Длина окружности и площадь круга»»
Тематический тест по теме «Длина окружности и площадь круга»
Четырехугольник является правильным, если:
а)все его углы равны между собой;
б)все его стороны равны между собой;
в)все его углы равны между собой и все его стороны равны между собой.
2. Длина окружности больше диаметра в….
а) 2 

3. Длина дуги окружности вычисляется по формуле:
а) l = 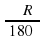
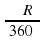
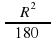
4. Сторона правильного треугольника, вписанного в окружность с радиусом R, равна:
а) R 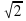
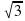
5. Отношение радиуса вписанной к радиусу описанной около квадрата окружности равно:
а) 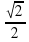
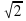
6. Отношение радиуса описанной к радиусу вписанной в правильный шестиугольник окружности равно:
а) 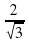
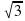
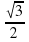
7. Каждый угол правильного десятиугольника равен:
а) 140 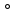
8. Внешний угол правильного двенадцатиугольника равен:
а) 36
9. Из круга, радиус которого равен 20 см, вырезан сектор. Дуга сектора равна 90
а) 100


10. Длина дуги окружности с радиусом 12 см и градусной мерой 100 
а) 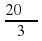
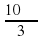
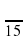
11. В окружность вписаны квадрат и правильный треугольник. Периметр треугольника равен 30 см, периметр квадрата равен:
а) 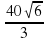
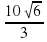
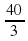
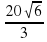
Тематический тест по теме «Длина окружности и площадь круга»
Если в четырехугольнике все стороны равны, то он:
а) всегда является правильным;
б) может быть правильным;
в) никогда не является правильным.
2. Длина окружности больше радиуса в
а) 2 

3. Площадь кругового сектора вычисляется по формуле:
а) S = 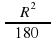
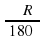
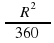
4. Сторона правильного четырехугольника, вписанного в окружность с радиусом R, равна:
а) R ; б) R 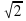
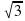
5. Отношение радиуса описанной к радиусу вписанной в квадрат окружности равно:
а) 2 ; б) 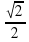
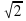
6. Отношение радиуса вписанной к радиусу описанной около правильного шестиугольника окружности равно:
а) 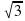
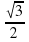
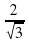
7. Каждый угол правильного восьмиугольника равен:
а) 135 
8. Внешний угол правильного двадцатиугольника равен:
а) 20
9. Из круга, радиус которого равен 30 см, вырезан сектор. Дуга сектора равна 60
а) 150


10. Длина дуги окружности с радиусом 6 см и градусной мерой равна 135 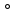
а) см; б) 9
11. Площадь круга равна 256
а) 16


Тематический тест по теме «Длина окружности и площадь круга»
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Презентация по геометрии на тему «Длина окружности и площадь круга» (9 класс)
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов
Сертификат и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Подготовить учащихся к контрольной работе. Совершенствовать навыки решения задач. Геометрия приближает разум к истине. Платон.
Проверочный тест 1вариант 1. Четырехугольник является правильным, если: а) все его углы равны между собой б) все его стороны равны между собой в) все его углы равны между собой и все его стороны равны между собой. 2. Длина окружности больше диаметра в …… а) 2П раз, б) П раз, в) 2 раза 3. Длина дуги окружности вычисляется по формуле : а) L=ПRß/180 б) L=ПRß/360 в) L=ПR2ß/180 4. Сторона правильного треугольника , вписанного в окружность с радиусом R, равна : а) R√2 б) R√3 в) R 5. Отношение радиуса вписанной к радиусу описанной около квадрата окружности равно: а) √2/2 б) 2 в) √2 6. Отношение радиуса описанной к радиусу вписанной в правильный шестиугольник окружности равно: а) 2/√3 б) √3 в) √3/2 7. Каждый угол правильного десятиугольника равен : а) 1400 б)1350 в)1440 8. Внешний угол правильного двенадцатиугольника равен : а) 360 б) 300 в) 450 9. Из круга , радиус которого равен 20см. вырезан сектор. Дуга сектора равна 900. Чему равна площадь оставшейся части круга. а) 100П см2 б) 400П см2 в) 300П см2. 10. Длина дуги окружности с радиусом 12см и градусной мерой 1000 равна: а) 20П/3 cм б) 10П/3 см в) П/15 см
Проверочный тест 2 вариант 1. Если в четырехугольнике все стороны равны, то он: а) всегда является правильным б) может быть правильным в) никогда не является правильным 2. Длина окружности больше радиуса в : а) 2П раз, б) П раз в) 2 раза 3. Площадь кругового сектора вычисляется по формуле: а) L=ПR2ß/180 б) L=ПRß/180 в) L=ПR2ß/360 4. Сторона правильного четырехугольника, вписанного в окружность с радиусом R, равна: а) R б) R√2 в) R√3 5. Отношение радиуса описанной к радиусу вписанной в квадрат окружности равно: а) 2 б) √2/2 в) √2 6. Отношение радиуса вписанной к радиусу описанной около правильного шестиугольника окружности равно: а) √3 б) √3/2 в) 2/√3 7. Каждый угол правильного восьмиугольника равен: а) 1350 б) 1440 в) 1400 8. Внешний угол правильного двадцатиугольника равен: а) 200 б) 22,50 в) 180 9. Из круга, радиус которого равен 30см, вырезан сектор. Дуга сектора равна 600. Чему равна площадь оставшейся части круга. а) 150П см2 б) 750П см2 в) 900П см2 10. Длина дуги окружности с радиусом 6см и градусной мерой 1350 равна: а) 9П/2 см б) 9П см в) 9П/4 см
Тест с последующей самопроверкой. 1.Один из внутренних углов правильного n-угольника равен 1500 . Найдите число сторон многоугольника. а) 9 б) 14 в) 12 г) 15 2. Периметр правильного треугольника равен 12 3 см. Найдите радиус вписанной окружности а) 2см б) 4см в) 4/ √3 г) 2/√ 3 3. Около квадрата описана окружность и в квадрат вписана окружность . Найдите отношение радиуса описанной окружности к радиусу вписанной окружности . а) 1/ √2 б) √2 в) 2 г) 1/2 4. Сторона правильного шестиугольника равна 2м . На сколько площадь описанного круга больше площади вписанного круга. а) 3√3 б) 3√ 3/ 4 в) 6√3 г) 3√3 / 2 5. Рис. Площадь полуокружности с центром в точке О равна 8П . Найдите площадь заштрихованной фигуры. а) 16П б) 8П в) 4П г) 32П 6. В окружности вписаны квадрат и правильный треугольник. Периметр треугольника равен 30см, периметр квадрата равен . а) 40√ 6/3 б) 10 √6 /3 в) 40 /3 г) 20 √6 /3 Ответы: 1-(в), 2-(а), 3- (б), 4- (г), 5- (б), 6- (а).
Вопросы: Чему равна сторона правильного ∆, описанного около круга радиуса r ? Выразите площадь треугольника через r ? Чему равна площадь круга радиуса r? Чему равна разность площадей ∆ и вписанную в него круга? Найдите радиус r. Задача1: Площадь правильного треугольника больше площади вписанного в него круга на 27√3 – 9П Решение: Пусть радиус вписанного круга равен r. Тогда площадь S=Пr². Сторона правильного ∆ , описанного около круга. Тогда S∆=½∙а3∙а3∙sin60°= ½∙2√3r∙√3/2=3∙√3∙r² Тогда S∆ — Sкр=3∙√3∙r²-Пr²=r²(3√3 — П) По условию задачи S∆ — Sкр=27∙√3 – 9П=9(3√3 — П), тогда r²(3√3 — П)=9(3√3 – П), r=3 Ответ: r=3
Вопросы: Чем являются радиусы ОА и ОВ, кругового сектора с дугой АЕВ? Постройте ∆ОСО1 . Какие элементы в данном ∆ известны? Как найти S незаштрихованной фигуры? Как найти S кругового сектора с дугой АЕВ? Задача2: В сектор с центральным углом в 60° и радиусом, равным 6см, вписана в окружность. Найдите площадь заштрихованной фигуры. Решение: Т.к. окружность вписана в сектор, то ОА и ОВ-касательные к окружности, тогда ОО1-биссектриса
🎬 Видео
Задание № 1088 — Геометрия 9 класс (Атанасян)Скачать

Задача 6 №27624 ЕГЭ по математике. Урок 71Скачать

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

№698. Сумма двух противоположных сторон описанного четырехугольника равна 12 см, а радиусСкачать

Задание № 1087 — Геометрия 9 класс (Атанасян)Скачать

Четырехугольники, вписанные в окружность. 9 класс.Скачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Если в четырёхугольник можно вписать окружностьСкачать

ЕГЭ Математика Задание 6#27952Скачать
Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Вписанные четырехугольники. 9 класс.Скачать

Вписанный в окружность четырёхугольник.Скачать

Задача 6 №27862 ЕГЭ по математике. Урок 105Скачать

9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

Формулы радиусов описанной и вписанной окружностей правильного многоугольника 2Скачать

Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

Задача 6 №27916 ЕГЭ по математике. Урок 133Скачать



