Помимо использования разных видов форматирования текста таких как: изменение шрифта, применение полужирного или курсивного начертания, иногда необходимо сделать верхнее подчеркивание в Ворде. Расположить черту над буквой довольно просто, рассмотрим несколько способов решения данной задачи.
- С помощью «Диакритических знаков»
- Подчеркивание сверху посредством фигуры
- Содержание
- Введение [ править | править код ]
- Примеры [ править | править код ]
- Непрерывная случайная величина [ править | править код ]
- Некоторые проблемы применения среднего [ править | править код ]
- Отсутствие робастности [ править | править код ]
- Сложный процент [ править | править код ]
- Направления [ править | править код ]
- Здесь легко и интересно общаться. Присоединяйся!
- Вставка математических знаков
- Доступные наборы символов
- ⃗ Надстрочный символ стрелка вправо
- Вектор, векторное поле, верхний индекс
- U+20D7
- Нажмите, чтобы скопировать и вставить символ
- Техническая информация
- Значение символа
- Свойства
- Похожие символы
- Кодировка
- Наборы с этим символом:
- 🎥 Видео
Видео:Как выражать вектор? Как решать задачу с вектором? | TutorOnlineСкачать

С помощью «Диакритических знаков»
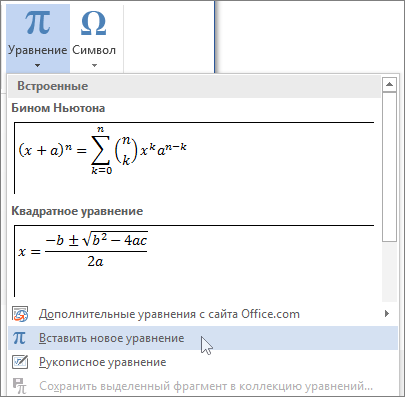
Благодаря панели символов сделать черточку сверху можно следующим образом. Установите курсор мыши в нужном месте по тексту. Перейдите во вкладку «Вставка» далее найдите и нажмите в области «Символы» на кнопку «Формула» и выберите из выпадающего меню «Вставить новую формулу».
Откроется дополнительная вкладка «Работа с формулами» или «Конструктор». Из представленных вариантов в области «Структуры» выберите «Диакритические знаки» и кликните по окну с названием «Черта».
В добавленном окне напечатайте необходимое слово или букву.
В результате получится такой вид.
Видео:Найдите разложение вектора по векторам (базису)Скачать

Подчеркивание сверху посредством фигуры
Используя фигуры в Ворде, можно подчеркнуть слово как сверху, так и снизу. Рассмотрим верхнее подчеркивание. Изначально необходимо напечатать нужный текст. Далее перейти во вкладку «Вставка» в области «Иллюстрации» выбрать кнопку «Фигуры». В новом окне кликнуть по фигуре «Линия».
Поставить крестик над словом в начале, нажать и протянуть линию до конца слова, двигая вверх или вниз выровнять линию и отпустить.
Можно изменить цвет верхнего подчеркивания, нужно нажать по линии и открыть вкладку «Формат». Нажав по кнопке «Контур фигуры» указать нужный цвет. Также можно изменить вид подчеркивания и толщину. Для этого перейдите в подпункт ниже «Толщина» или «Штрихи».
В соответствии с настройками палочку можно преобразовать в штрихпунктирную линию, либо изменить на стрелку, в нужном направлении.
Благодаря таким простым вариантам, поставить черту над буквой или цифрой не займёт много времени. Стоит лишь выбрать наиболее подходящий способ из вышепредставленных.
Сре́днее арифмети́ческое (в математике и статистике) множества чисел — число, равное сумме всех чисел множества, делённой на их количество. Является одной из наиболее распространённых мер центральной тенденции.
Частными случаями среднего арифметического являются среднее (генеральной совокупности) и выборочное среднее (выборки).
При стремлении количества элементов множества чисел стационарного случайного процесса к бесконечности среднее арифметическое стремится к математическому ожиданию случайной величины.
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Содержание
Видео:Математика это не ИсламСкачать

Введение [ править | править код ]
Обозначим множество чисел X = (x1, x2, …, xn), тогда выборочное среднее обычно обозначается горизонтальной чертой над переменной ( x ¯ >> 
Для обозначения среднего арифметического всей совокупности чисел обычно используется греческая буква μ. Для случайной величины, для которой определено среднее значение, μ есть вероятностное среднее или математическое ожидание случайной величины. Если множество X является совокупностью случайных чисел с вероятностным средним μ, тогда для любой выборки xi из этой совокупности μ = E есть математическое ожидание этой выборки.
На практике разница между μ и x ¯ >> 

Обе эти величины вычисляются одним и тем же способом:
x ¯ = 1 n ∑ i = 1 n x i = 1 n ( x 1 + ⋯ + x n ) . >= >sum _^ x_= >(x_ +cdots +x_ ).>
Если X — случайная переменная, тогда математическое ожидание X можно рассматривать как среднее арифметическое значений в повторяющихся измерениях величины X. Это является проявлением закона больших чисел. Поэтому выборочное среднее используется для оценки неизвестного математического ожидания.
В элементарной алгебре доказано, что среднее n + 1 чисел больше среднего n чисел тогда и только тогда, когда новое число больше чем старое среднее, меньше тогда и только тогда, когда новое число меньше среднего, и не меняется тогда и только тогда, когда новое число равно среднему. Чем больше n, тем меньше различие между новым и старым средними значениями.
Примеры [ править | править код ]
- Для получения среднего арифметического трёх чисел необходимо сложить их и разделить на 3:
x 1 + x 2 + x 3 3 . +x_ +x_ > >.>
- Для получения среднего арифметического четырёх чисел необходимо сложить их и разделить на 4:
x 1 + x 2 + x 3 + x 4 4 . +x_ +x_ +x_ > >.>
Непрерывная случайная величина [ править | править код ]
Если существует интеграл от некоторой функции f ( x ) 

f ( x ) ¯ [ a ; b ] = 1 b − a ∫ a b f ( x ) d x . _ = >int _^f(x)dx.>
Здесь подразумевается, что a.>»> b > a . a.> 
Видео:Разложение вектора по векторам (базису). Аналитическая геометрия-1Скачать

Некоторые проблемы применения среднего [ править | править код ]
Отсутствие робастности [ править | править код ]
Хотя среднее арифметическое часто используется в качестве средних значений или центральных тенденций, это понятие не относится к робастной статистике, что означает, что среднее арифметическое подвержено сильному влиянию «больших отклонений». Примечательно, что для распределений с большим коэффициентом асимметрии среднее арифметическое может не соответствовать понятию «среднего», а значения среднего из робастной статистики (например, медиана) может лучше описывать центральную тенденцию.
Классическим примером является подсчёт среднего дохода. Арифметическое среднее может быть неправильно истолковано в качестве медианы, из-за чего может быть сделан вывод, что людей с большим доходом больше, чем на самом деле. «Средний» доход истолковывается таким образом, что доходы большинства людей находятся вблизи этого числа. Этот «средний» (в смысле среднего арифметического) доход является выше, чем доходы большинства людей, так как высокий доход с большим отклонением от среднего делает сильный перекос среднего арифметического (в отличие от этого, средний доход по медиане «сопротивляется» такому перекосу). Однако, этот «средний» доход ничего не говорит о количестве людей вблизи медианного дохода (и не говорит ничего о количестве людей вблизи модального дохода). Тем не менее, если легкомысленно отнестись к понятиям «среднего» и «большинство народа», то можно сделать неверный вывод о том, что большинство людей имеют доходы выше, чем они есть на самом деле. Например, отчёт о «среднем» чистом доходе в Медине, штат Вашингтон, подсчитанный как среднее арифметическое всех ежегодных чистых доходов жителей, даст на удивление большое число из-за Билла Гейтса. Рассмотрим выборку (1, 2, 2, 2, 3, 9). Среднее арифметическое равно 3.17, но пять значений из шести ниже этого среднего.
Сложный процент [ править | править код ]
Если числа перемножать, а не складывать, нужно использовать среднее геометрическое, а не среднее арифметическое. Наиболее часто этот казус случается при расчёте окупаемости инвестиций в финансах.
Например, если акции в первый год упали на 10 %, а во второй год выросли на 30 %, тогда некорректно вычислять «среднее» увеличение за эти два года как среднее арифметическое (−10 % + 30 %) / 2 = 10 %; правильное среднее значение в этом случае дают совокупные ежегодные темпы роста, по которым годовой рост получается только около 8,16653826392 % ≈ 8,2 %.
Причина этого в том, что проценты имеют каждый раз новую стартовую точку: 30 % — это 30 % от меньшего, чем цена в начале первого года, числа: если акции в начале стоили $30 и упали на 10 %, они в начале второго года стоят $27. Если акции выросли на 30 %, они в конце второго года стоят $35.1. Арифметическое среднее этого роста 10 %, но поскольку акции выросли за 2 года всего на $5.1, средний рост в 8,2 % даёт конечный результат $35.1:
[$30 (1 — 0.1) (1 + 0.3) = $30 (1 + 0.082) (1 + 0.082) = $35.1]. Если же использовать таким же образом среднее арифметическое значение 10 %, мы не получим фактическое значение: [$30 (1 + 0.1) (1 + 0.1) = $36.3].
Сложный процент в конце 2 года: 90 % * 130 % = 117 % , то есть общий прирост 17 %, а среднегодовой сложный процент 117 % ≈ 108.2 % >approx 108.2%> 
Направления [ править | править код ]
При расчёте среднего арифметического значений некоторой переменной, изменяющейся циклически (например, фаза или угол), следует проявлять особую осторожность. Например, среднее чисел 1° и 359° будет равно 1 ∘ + 359 ∘ 2 = +359^ > >=> 
- Во-первых, угловые меры определены только для диапазона от 0° до 360° (или от 0 до 2π при измерении в радианах). Таким образом, ту же пару чисел можно было бы записать как (1° и −1°) или как (1° и 719°). Средние значения каждой из пар будут отличаться: 1 ∘ + ( − 1 ∘ ) 2 = 0 ∘ +(-1^ )> >=0^ >
, 1 ∘ + 719 ∘ 2 = 360 ∘ +719^ > >=360^ >
.
- Во-вторых, в данном случае, значение 0° (эквивалентное 360°) будет геометрически лучшим средним значением, так как числа отклоняются от 0° меньше, чем от какого-либо другого значения (у значения 0° наименьшая дисперсия). Сравните:
- число 1° отклоняется от 0° всего на 1°;
- число 1° отклоняется от вычисленного среднего, равного 180°, на 179°.
Среднее значение для циклической переменной, рассчитанное по приведённой формуле, будет искусственно сдвинуто относительно настоящего среднего к середине числового диапазона. Из-за этого среднее рассчитывается другим способом, а именно, в качестве среднего значения выбирается число с наименьшей дисперсией (центральная точка). Также вместо вычитания используется модульное расстояние (то есть, расстояние по окружности). Например, модульное расстояние между 1° и 359° равно 2°, а не 358° (на окружности между 359° и 360°==0° — один градус, между 0° и 1° — тоже 1°, в сумме — 2°).
Здесь легко и интересно общаться. Присоединяйся!
в ворде набирай код – маркер перед знаком.
знак у, код 035F,Alt+X : результат ͟y снизу
k, 035E,Alt+X ; результат ͞k – сверху.
В символах есть коды. и волнистых, и прочих…: )
если в ворде то вставить символ или надстрочным шрифтом (в свойствах шривта поставить галочку надстрочныу и в нужном месте поставить черточку)
В ворде есть переход в формулы жми:
ВСТАВКА – ФОРМУЛЫ – ДИАКРИТИЧЕСКИЕ ЗНАКИ и выбирай знак, в квадратике пиши переменную.
А так есть мастера формул. Международный – это MathType. В нём можно сделать всё, только язык надо зхнать : TeX
Видео:Написать разложение вектора x по векторам p, q, r. Разложение вектора по базису из трёх векторов.Скачать

Вставка математических знаков
В Word можно вставлять математические символы в уравнения и текст.
На вкладке Вставка в группе Символы щелкните стрелку рядом с надписью Формула и выберите Вставить новую формулу.
В области Работа с формулами в группе Символы на вкладке Конструктор щелкните стрелку Еще.
Щелкните стрелку рядом с именем набора символов, а затем выберите набор символов, который вы хотите отобразить.
Щелкните нужный символ.
Видео:Разложение вектора по базису. 9 класс.Скачать

Доступные наборы символов
В группе Символы в Word доступны указанные ниже наборы математических символов. Щелкнув стрелку Еще, выберите меню в верхней части списка символов, чтобы просмотреть группы знаков.
Основные математические символы
Часто используемые математические символы, такие как > и
Видео:Как разложить вектор по базису - bezbotvyСкачать

⃗ Надстрочный символ стрелка вправо
Видео:Вектор А - Напоследок (Official mood video)Скачать

Вектор, векторное поле, верхний индекс
Видео:Проекция вектора на вектор.Скачать

U+20D7
Видео:Собственные векторы и собственные значения матрицыСкачать

Нажмите, чтобы скопировать и вставить символ
Видео:Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Техническая информация
| Название в Юникоде | Combining Right Arrow Above |
| Номер в Юникоде | |
| Раздел | Комбинируемые диакритические знаки для символов |
| Версия Юникода: | 1.1 (1993) |
Видео:Образуют ли данные векторы базисСкачать

Значение символа
В геометрии, надстрочной стрелкой обозначается вектор — прямой отрезок имеющий начало и конец.
Символ «Надстрочный символ стрелка вправо» был утвержден как часть Юникода версии 1.1 в 1993 г.
Видео:Трассировка. Как сделать изображение векторным? Какие картинки подойдут оптимально? Corel DrawСкачать

Свойства
| Версия | 1.1 |
| Блок | Комбинируемые диакритические знаки для символов |
| Тип парной зеркальной скобки (bidi) | Нет |
| Композиционное исключение | Нет |
| Изменение регистра | 20D7 |
| Простое изменение регистра | 20D7 |
Видео:ТРАССИРОВКА - АВТОМАТИЧЕСКИЙ ПЕРЕВОД РАСТРА В ВЕКТОР. ЭТО ДОЛЖЕН УМЕТЬ КАЖДЫЙ! КОРЕЛ. COREL.Скачать

Похожие символы
Надстрочный символ По часовой стрелке
Надстрочный символ стрелка влево
Короткая стрелка, указывающая направо.
Длинная стрелка, указывающая налево.
Длинная стрелка, указывающая направо.
Стрелка вправо над стрелкой влево
Стрелка влево, упирающаяся в планку.
С-образная правая стрелка против.
Стрелка влево-вправо с чертой
Волнистая стрелка влево-вправо
Лево право белая стрелка
Стрелка влево-вправо с двойным.
Двойная стрелка влево-вправо
Видео:Собственные значения и собственные векторы матрицы (4)Скачать

Кодировка
| Кодировка | hex | dec (bytes) | dec | binary |
|---|---|---|---|---|
| UTF-8 | E2 83 97 | 226 131 151 | 14844823 | 11100010 10000011 10010111 |
| UTF-16BE | 20 D7 | 32 215 | 8407 | 00100000 11010111 |
| UTF-16LE | D7 20 | 215 32 | 55072 | 11010111 00100000 |
| UTF-32BE | 00 00 20 D7 | 0 0 32 215 | 8407 | 00000000 00000000 00100000 11010111 |
| UTF-32LE | D7 20 00 00 | 215 32 0 0 | 3609198592 | 11010111 00100000 00000000 00000000 |
Видео:Vector W8 - это безумнейший когда-либо выпускавшийся суперкарСкачать

Наборы с этим символом:
© Таблица символов Юникода, 2012–2022.
Юникод® — это зарегистрированная торговая марка консорциума Юникод в США и других странах. Этот сайт никак не связан с консорциумом Юникод. Официальный сайт Юникода располагается по адресу www.unicode.org.
Мы используем 🍪cookie, чтобы сделать сайт максимально удобным для вас. Подробнее
🎥 Видео
Вектор А — В порядке (Official video)Скачать

ВЕКТОРЫ 9 класс С НУЛЯ | Математика ОГЭ 2023 | УмскулСкачать

Криминальный бит, Вектор А - ВыживатьСкачать