Через точку пересечения медиан треугольника abc параллельно прямой ав проведена плоскость

Через точку пересечения медиан треугольника ABC параллельно прямой AB проведена прямая пересекающая стороны AC и BC в точках D и E соответственно. Найдите отрезок DE, если AB = 18 см

Объяснение:

1) АМ=МВ=9 см . По т. о точке пересечения медиан .

2) Т.к. стороны угла ∠ВСМ пересекают две параллельные прямые АВ и DE, по т. о пропорциональных отрезках или

3) Т.к. стороны угла ∠АСМ пересекают две параллельные прямые АВ и DE, по т. о пропорциональных отрезках или

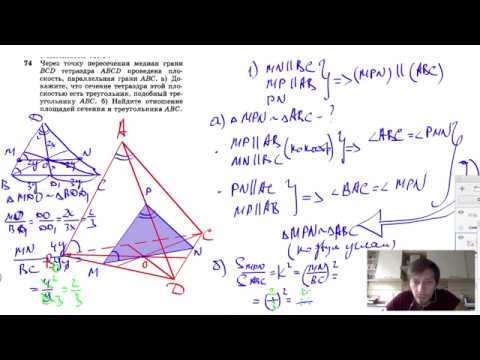
Видео:№74. Через точку пересечения медиан грани BCD тетраэдра ABCD проведена плоскостьСкачать

Через точку пересечения медиан треугольника abc параллельно прямой ав проведена плоскость

Точки A, B, C и D не лежат в одной плоскости. Определите, в каком отношении плоскость, проведённая через точку пересечения медиан треугольника ABC параллельно прямым AB и CD, делит медиану, проведённую к стороне CD треугольника ACD.

Так как данная плоскость параллельна прямым AB и CD, то она пересекает плоскости ABC и ACD по прямым A₁B₁ и B₁C₁, соответственно параллельным AB и CD. Таким образом, A₁B₁C₁ — это искомая плоскость, а AP : PN — искомое отношение.

Треугольники ANC и APB₁ подобны по двум углам ( — общий, как соответственные при , AN — секущая). Тогда Аналогично, треугольники CLA и CMB₁ подобны по двум углам. Тогда

Так как M — точка пересечения медиан, CL — медиана треугольника ABC, то по свойству медиан . Тогда получим

Видео:№245. Через точку пересечения биссектрис ВВ1 и СС1 треугольника ABC проведена прямая, параллельнаяСкачать

Применение теорем Менелая и Чевы для решения задач

В пункте 1.5 данной курсовой работы мы рассмотрели теоремы Чевы и Менелая, теперь рассмотри практическое использование данных теорем на примерах.

В треугольнике АВС на стороне ВС взята точка N так, что NC = 3BN; на продолжении стороны АС за точку А взята точка М так, что МА = АС. Прямая MN пересекает сторону АВ в точке F. Найти отношение Решение:

По условию задачи МА = АС, NC = 3BN. Пусть MA = AC =b, BN = k, NC = 3k. Прямая MN пересекает две стороны треугольника АВС и продолжение третьей.

По теореме Менелая

Докажите, что медианы треугольника пересекаются в одной точке.

Пусть AM₁, BM₂, СM₃ — медианы треугольника АВС. Чтобы доказать, что эти отрезки пересекаются в одной точке, достаточно показать, что

Тогда по теореме Чевы (обратной) отрезки AM₁, BM₂ и СM₃ пересекаются в одной точке.

Итак, доказано, что медианы треугольника пересекаются в одной точке.

На стороне PQ треугольника PQR взята точка N, а на стороне PR — точка L, причем NQ = LR. Точка пересечения отрезков QL и NR делит QL в отношении m:n, считая от точки Q. Найдите

По условию NQ = LR, Пусть NA = LR =a, QF = km, LF = kn. Прямая NR пересекает две стороны треугольника PQL и продолжение третьей.

По теореме Менелая

Докажите, что биссектрисы треугольника пересекаются в одной точке.

Тогда по теореме Чевы (обратной) AL₁, BL₂, CL₃ пересекаются в одной точке. По свойству биссектрис треугольника

Перемножая почленно полученные равенства, получаем

Для биссектрис треугольника равенство Чевы выполняется, следовательно, они пересекаются в одной точке.

В треугольнике АВС AD — медиана, точка O — середина медианы. Прямая ВО пересекает сторону АС в точке К. В каком отношении точка К делит АС, считая от точки А?

Пусть BD = DC = a, AO = OD = m. Прямая ВК пересекает две стороны и продолжение третьей стороны треугольника ADC.

По теореме Менелая

Докажите, если в треугольник вписана окружность, то отрезки, соединяющие вершины треугольника с точками касания противоположных сторон, пересекаются в одной точке.

Пусть A₁, B₁и C₁ — точки касания вписанной окружности треугольника АВС. Для того чтобы доказать, что отрезки AA₁, BB₁и CC₁ пересекаются в одной точке, достаточно показать, что выполняется равенство Чевы:

Используя свойство касательных, проведенных к окружности из одной точки, введем обозначения: C₁B = BA₁ = x, AC₁ = CB₁ = y, BA₁ = AC₁ = z.

Равенство Чевы выполняется, значит, биссектрисы треугольника пересекаются в одной точке.

Рассмотрим два способа решения одной задачи. Первый способ довольно длинный, но данный прием, который в нем используется, применяется довольно часто при решении задач, в которых дано отношение отрезков. Второй способ позволяет решить задачу в одно действие, но в нем используется Теорема Менелая.

Итак задача: На сторонах AB и BC треугольника ABC взяты соответственно точки M и N так, что AM:MB=2:3, BN:NC=2:1. Отрезки AN и CM пересекаются в точке O. Найти отношение CO:OM.

Вот наш треугольник:

Проведем через точку В прямую параллельно отрезку AB, затем продолжим отрезок AN до пересечения с этой прямой и поставим там точку К:

Рассмотрим треугольники ANC и BNK. Эти треугольники подобны, так как AC||BK. Стороны треугольника BNK относятся к сторонам треугольника ANC как 2:1.

Пусть AC = x, BK = 2x.

Теперь продолжим отрезок MC до пересечения с прямой BK. Поставим там точку L.

Мы получили подобные треугольники LMB и AMC, сходственные стороны которых относятся как 3:2. Так как AC = x, то LB = 1,5x.

Пусть LM = 3n, MC = 2n. Тогда LC = 5n.

Теперь рассмотрим подобные треугольники LOK и AOC.

следовательно, . Пусть LO = 3,5z, OC = z. Тогда LO+OC=LC=4,5z. Получили, что 5n = 4,5z. Тогда MC = 2n = z.

Отсюда MO = MC-CO = z-z = z

Отсюда CO:OM = z:z = 5:4 = 1,25.

Теперь используем при решении данной задачи теорему Минелая. Рассмотрим треугольник MBC и прямую AN:

Запишем теорему Менелая для этого треугольника:

Рассмотрев применение теорем Чевы и Менелая при решении задач можно сделать следующий вывод: знание данных теорем весьма упрощает решение задачи, однако зачастую задачу все таки можно решить и не применяя данных теорем, но, как правило, решение будет весьма объёмным.

💡 Видео

Точка пересечения медиан в треугольникеСкачать

Теорема о точке пересечения медиан треугольника. Доказательство. 8 класс.Скачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

№366. Докажите, что если М — точка пересечения медиан треугольника ABC, а О — произвольная точкаСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Через середину К медианы ВМ треугольника АВС и вершину А проведена прямая пересекающая сторону ВС вСкачать

Параллельные прямые | Математика | TutorOnlineСкачать

№122. Прямая CD перпендикулярна к плоскости правильного треугольника ABC. Через центр О этогоСкачать

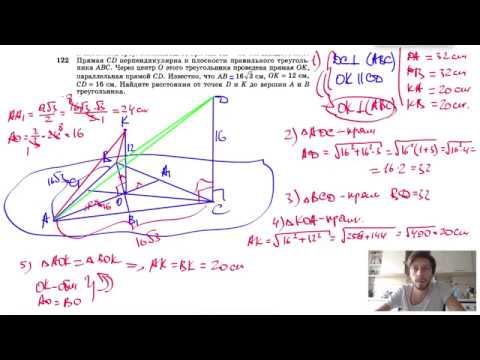
Определение кратчайшей расстоянии от точки до плоскостиСкачать

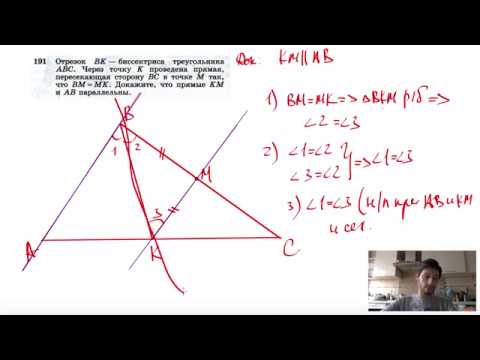
№191. Отрезок ВК — биссектриса треугольника ABC. Через точку К проведена прямая, пересекающаяСкачать

№150. Через вершину А прямоугольника ABCD проведена прямая АК, перпендикулярная к плоскостиСкачать

Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

№120. Через точку О пересечения диагоналей квадрата со стороной а проведена прямая ОКСкачать

№158. Через вершину В ромба ABCD проведена прямая ВМ, перпендикулярная к его плоскости. НайдитеСкачать

Точка пересечения медиан.Скачать

Лекция 2. Основная задача начертательной геометрии. Точка пересечения прямой с плоскостью.Скачать