Спираль из центра окружности

Спиралью называется плоская кривая, описываемая точкой, удаляющейся от центра при совершении кругового движения в плоскости чертежа вокруг центра спирали. На практике различают спирали с постоянным и постепенно возрастающим расстоянием между завитками. Обычно спирали строят по точкам и вычерчивают с помощью лекала.

Для того чтобы расчертить спираль, необходимо наметить не менее двух ее центров. Если вычерчивают спираль из трех или более центров, то обычно центрами спирали являются вершины правильного треугольника или правильного многоугольника. Каждую дугу проводят из последующей вершины до пересечения с лучом из угла треугольника или многоугольника. Радиус при этом каждый раз увеличивается на длину, равную длине стороны треугольника или многоугольника.

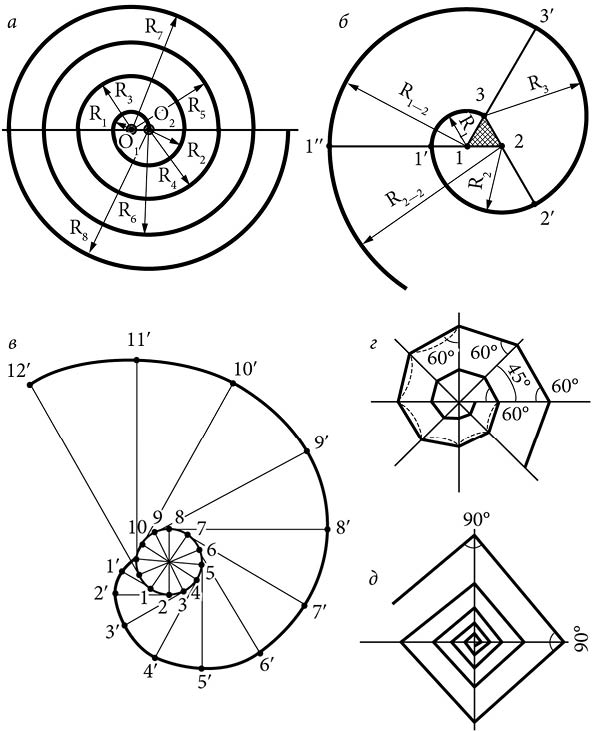
Рассмотрим, например, как начертить так называемую «архимедову спираль» (рис. 17, а ). Для этого нужно провести горизонтальную линию и отметить на ней две точки О 1 и О 2, отстоящие одна от другой примерно на 3 мм. Поставив ножку циркуля в одну из этих точек (О 1), проведите дугу радиусом 3 мм (R 1), равную половине окружности. Концы этой дуги должны опираться на горизонтальную ось (в данном примере – сверху).

Затем перенесите ножку циркуля во вторую из отмеченных точек и увеличьте его раствор так, чтобы карандаш попал в конец первой дуги. Снова проведите половину окружности радиусом R 2, опирающуюся на горизонтальную линию, но уже с противоположной стороны (снизу). Таким же образом, переставляя ножку циркуля то в первую, то во вторую точку и каждый раз увеличивая его раствор, продолжайте разворачивать спираль. На рис. 17, а , изображено четыре полных оборота.

Для построения спирали, имеющей три центра (рис. 17, б), находящихся на равных расстояниях один от другого, необходимо предварительно построить равносторонний треугольник 1–2–3 (заштрихован) и продолжить его стороны так, как это показано на рисунке (линии 1–1’, 2–2’ и 3–3’ ).

Из центра 1 проводим дугу 3–1’ радиусом R 1, равным длине стороны треугольника, до пересечения с продолжением стороны 1–1’ . Затем из центра 2 описываем дугу радиусом R 2 = 2R 1 до пересечения с продолжением стороны 2 (линия 2–2’ ). После этого из центра 3 проводим дугу радиусом R 3 = 3R 1 до пересечения с продолжением стороны 3 (линия 3–3’ ) в точке 3’ . После этого возвращаемся в центр 1 и продолжаем построение в такой же последовательности, каждый раз увеличивая радиус дуги на величину стороны треугольника.

Рис. 17. Построение спиралей: а – «архимедова спираль» с двумя центрами; б – трехцентровая спираль; в – эвольвента круга; г, д – ломаные (хордовые) спирали.

Аналогично выполняют спирали с четырьмя, пятью и т. д. центрами.

Эвольвента круга (рис. 17, в ) – это плоская кривая, образуемая точкой на прямой, которая перемещается без скольжения по неподвижной окружности заданного радиуса. Эта кривая иногда называется разверткой окружности. Построение эвольвенты начинается с деления заданной окружности на произвольное число равных частей, например 12. В каждой точке деления проводим касательные к окружности. На каждой из этих касательных последовательно откладываем длину окружности, равную πd /12: в точке 1 – πd /12, в точке 2 – 2πd /12, в точке 3 – 3πd /12 и т. д. На касательной к точке 12 откладываем длину окружности, равную πd . Соединяя последовательно плавной кривой по лекалу полученные на касательных точки 1’, 2’, 3’ и т. д., получим кривую, называемую эвольвентой.

Схема построения ломаных спиралей показана на рис. 17, г, д . Они строятся так же, как и циркульные, но дуги заменяются соответствующими хордами.

Золотая спираль или спираль Фибоначчи — логарифмическая спираль, коэффициент роста которой равен φ 4 , где φ — золотое сечение. Коэффициент роста логарифмической спирали показывает во сколько раз изменился полярный радиус спирали при повороте на угол 360°. [1] Свое название эта спираль получила из-за связи с последовательностью вложенных друг в друга прямоугольников с отношением сторон, равным φ , которые принято называть золотыми. Золотую спираль можно как вписать в систему таких прямоугольников, так и описать вокруг нее. Популярность золотая спираль приобрела из-за того, что известная с начала XVI века и применяющаяся в искусстве [2] спираль, построенная по методу Дюрера [3] [4] , оказалась хорошей аппроксимацией для золотой спирали (см. рисунок)

Видео:Лекальные кривые. Спираль Архимеда. Эвольвента окружности. ЦиклоидаСкачать

Содержание

Видео:Спираль Архимеда построениеСкачать

Формула [ править | править код ]

Уравнение для золотой спирали в полярной системе координат то же самое, что и для других логарифмических спиралей, но со специальным значением коэффициента роста – φ 4 :

r = a φ ± 2 θ π >> ,

где a — произвольная положительная вещественная константа, а φ = 5 + 1 2 >+1> >> — золотое сечение.

Основное свойство логарифмической спирали: угол между радиус-вектором, исходящим из полюса, и касательной к спирали – μ – постоянен, и для золотой спирали определяется формулой:

tg ⁡ μ = r r ′ = π 2 ln ⁡ φ mu = , где r ′ =”” d r d θ >> .

Откуда μ ≈ 73 ∘ > .

Видео:4K Приближенное построение золотой спирали, golden spiral approximationСкачать

Приближения золотой спирали [ править | править код ]

Существует несколько похожих спиралей, которые близки, но не совпадают в точности с золотой спиралью [5] , с которой их часто путают.

Как уже было написано выше, при вписывании золотой спирали в последовательность вложенных друг в друга золотых прямоугольников, она аппроксимируется спиралью, построенной по методу Дюрера. Золотой прямоугольник можно разделить на квадрат и подобный ему прямоугольник, его, в свою очередь, разделить тем же образом, и продолжать этот процесс произвольное число раз. Если в эти квадраты вписать соединенные между собой четвертинки окружностей, то получается спираль, изображенная на первом рисунке.

Ещё одной аппроксимацией является спираль Фибоначчи, которая строится подобно вышеописанной спирали, за исключением того, что начинают с прямоугольника из двух квадратов и добавляют потом к большей стороне прямоугольника квадрат такой же длины. Поскольку отношение между соседними числами Фибоначчи стремится к золотой пропорции, спираль всё больше приближается к золотой спирали по мере добавления квадратов (см. второй рисунок).

Видео:Построение эвольвенты окружностиСкачать

Спирали в природе [ править | править код ]

В природе встречаются приближения к логарифмическим спиралям с коэффициентом роста равным φ k . Так раковины моллюсков Nautilus pompilius и окаменелых аммонитов хорошо описываются при k = 2, а раковины некоторых улиток при k = 1. [6] Отношение длин трех витков спирали уха у человека равно φ [7] , что соответствует спирали с k = 1. Рукава спиральных галактик, несмотря на существующие утверждения [8] , если и описываются логарифмической, то не золотой спиралью. В данном случае, описание ею является проявлением случайной близости. Недавний анализ спиралей, встречающихся в роговичном эпителии мышей, показал, что там встречаются как золотая, так и другие логарифмические спирали. [9]

Построение спирали Архимеда.

Спираль Архимеда – это траектория точки, движущейся с постоянной скоростью от центра окружности по

радиусу, вращающемуся также с постоянной угловой скоростью.

1. Делим радиус окружности на одинаковое число равных частей (в примере на 8).

2. Делим окружность на такое же число равных частей.

3. Проводим лучи из центра через точки деления окружности.

4. На первом луче откладываем одно деление радиуса.

5. На втором луче откладываем два деления радиуса и т. д.

6. Если строить спираль дальше, то на луче 1 откладываем 8+1 деление радиуса (получаем точку IX ).

7. На втором луче откладываем 8+2 деления радиуса (получаем точку X) .

8. На третьем луче откладываем 8+3 деления радиуса (получаем точку XI) и т. д.

Соединяем точки по лекалу.

Спираль. Спираль Архимеда. Построение спирали Архимеда.

Видео:Числовая спиральСкачать

Геометрический дизайн: работа с кругами

Russian (Pусский) translation by Sergey Zhuk (you can also view the original English article)

Мы уже широко использовали круги для создания различных сеток для нескольких шаблонов. В этом уроке мы используем круги ради них, а именно в двух типах конструкций: спирали и вписанные круги.

Видео:Как решать задачи по программированию. Пример: задача "Спираль"Скачать

Спирали

Спирали бывают разных типов. Расстояние между поворотами и углом поворота определяет их внешний вид. Некоторые могут быть определены с помощью математического уравнения, которое переводит для конкретных спиралей в простые геометрические конструкции — приблизительные, но достаточно хорошие для глаза.

Обычная или архимедова спираль

Эта спираль определяется равным расстоянием между струнами, так что она имеет концентрический внешний вид. Она рисуется перемещением точки циркуля из одной точки в другую в базовой фигуре, которая может быть сегментом (двумя точками), треугольником, квадратом и т.д. Чем больше точек, тем плотнее и совершеннее спираль, но поскольку это также делает конструкцию более утомительной, шестиугольник является самым высоким, как правило.

Спираль, построенная по двум точкам

Шаг 1

На горизонтальной линии нарисуйте полукруг, маленький насколько это возможно. Это первый поворот спирали, и две точки, где он пересекает линию, являются точками построения.

Шаг 2

Поместите циркуль в одну из точек, откройте его, чтобы встретить другого, и нарисуйте полукруг на другой стороне линии. Две полуокружности образуют непрерывную кривую.

Шаг 3

Переместите циркуль назад к первой точке, откройте его, чтобы встретить конец кривой, и нарисуйте еще один полукруг.

Шаг 4

Продолжайте в этом ключе, перемещая циркуль из одной из точек построения в другую и каждый раз настраивая открытие, чтобы взять кривые, где вы остановились.

Продолжайте сколько угодно. Спираль будет выглядеть так:

Спираль, построенная на трех точках

Метод тот же, но мы начинаем с равностороннего треугольника, стороны которого расширены. Циркуль будет перемещаться из пункта 1 в 2 в 3, затем обратно в 1 и так далее. Если стороны вытянуты, как показано здесь, спираль поворачивается по часовой стрелке (и циркуль перемещается от точки к точке по часовой стрелке).

Шаг 1

Нарисуйте первую дугу.

Шаг 2

Переместитесь к следующей точке, отрегулируйте отверстие и нарисуйте следующую дугу.

Шаг 3

Переместитесь в третью точку и повторите.

После нескольких поворотов спираль выглядит так:

Спираль, построенная на четырех точках

Наша база теперь квадратная, и мы по-прежнему работаем по часовой стрелке. По мере того, как угол поворота уменьшается (сначала он составлял 180º для каждого, затем 120º, теперь для 90º), спираль становится более гладкой.

Шаг 1

Нарисуйте первый четверть круга.

Шаг 2

Перейдите ко второй точке, отрегулируйте раскрытие циркуля и нарисуйте следующий четверть круга.

Шаг 3

Повторите с третьей и четвертой точками.

Шаг 4

Как выглядит спираль за несколькими оборотами:

Спираль, построенная на шести точках

С шестиугольником в качестве основания, конструкция действительно такая же. Важнейшей составляющей является очень точное рисование оснований и расширение их сторон. Затем просто пробегите шесть пунктов:

Спираль через несколько оборотов:

Когда эти спирали располагаются бок о бок, мы можем оценить, насколько они более плавные и идеально круговые, когда база имеет большее количество точек.

Золотая спираль

В отличие от регулярных спиралей выше, расстояние между последовательными поворотами в логарифмических спиралях растет в геометрической последовательности. Такие спирали, обнаруженные в росте многих организмов, являются автомодельными: размер спирали увеличивается, но ее форма не изменяется (для этого ее также называли спира мирабилис, «чудо-спираль»). Золотая спираль — это тип логарифмической спирали с фактором роста, связанным с Золотым числом.

Самый простой способ нарисовать такую спираль — начать с ее внешних границ, в отличие от предыдущей. Поэтому мы начнем с построения золотого прямоугольника (я объясню, что это такое, когда это сделано).

Шаг 1

Построить квадрат. (Забыл как? См. Раздел Работа с 4 и 8.)

Шаг 2

Растяните стороны AB и DC.

Шаг 3

С точкой на E и циркулем, открытым для EC, нарисуйте дугу, которая разрезает расширенный AB на G.

Шаг 4

Переместите черновую точку на F и нарисуйте дугу, которая разрезает расширенный CD на H.

Шаг 5

Соедините к GH, чтобы закончить прямоугольник.

Это называется золотым прямоугольником, потому что AB/AG = BG/AB, другими словами отношение длинной стороны ко всему сегменту такое же, как отношение более короткой стороны к более длинной.

Бумага формата A4 (или любой другой размер в серии A) является золотым прямоугольником, поэтому вы можете использовать его общую поверхность в качестве внешнего прямоугольника и перейти сразу к шагу 6.

Шаг 6.

Теперь нам нужно разбить этот прямоугольник на квадраты. У нас уже есть первый квадрат. Следующий будет выведен из прямоугольника BGHC.

Поместите черновую точку на B и откройте ее на длину короткого сегмента. Отметьте I в BC.

Переместите черновую точку в G и отметьте J на GH.

Шаг 7.

Соедините IJ: теперь у нас есть квадрат BGJI, и новый прямоугольник остался.

Шаг 8

Повторите эту операцию в каждом последующем прямоугольнике, всегда создавая квадрат относительно внешнего края прямоугольника.

Когда у нас будет достаточно квадратов или они станут слишком маленькими для работы, мы можем нарисовать спираль.

Шаг 9

Поместите черновую точку на C, пусть отверстие будет равняться стороне первого квадрата, и нарисуйте четверть окружности DB.

Шаг 10

Переместите черновую точку на I, уменьшите отверстие в сторону второго квадрата и нарисуйте дугу BJ.

И так далее по всем квадратам .

Чувство этой спирали сильно отличается от концентрического и даже статического появления регулярных спиралей: оно гораздо менее сложенное, с динамическим движением.

Видео:Деление окружности на 3; 6; 12 равных частейСкачать

Вписанные круги

Круги могут быть вписаны, то есть втянуты внутрь фигуры таким образом, чтобы касаться ее сторон, под углами, многоугольниками или другими кругами. Это устройство является основой большей части декоративной геометрии Запада, например, в кельтском освещении или готических розовых окнах. Мы рассмотрим две базовые конструкции, которые мы можем использовать с любым многоугольником или любым количеством кругов внутри круга, а затем построить два полноценных окна с их узором.

Круг в секторе

Этот метод позволяет вам подбирать количество кругов по вашему выбору внутри круга. Начните с разделения круга равномерно на нужное количество разделов, затем для каждого сектора выполните следующее. Показанный здесь сектор состоит из круга, разделенного на шесть.

Шаг 1

Разделите сектор пополам. Биссектриса режет дугу в точке Q.

Шаг 2

Теперь нам нужно провести перпендикуляр к PQ в Q. С черновой точкой компаса на Q и любым отверстием нарисуйте дугу, которая разрезает биссектрису в точке A.

Шаг 3

Переместите сухую точку в A и нарисуйте еще одну дугу, разрезав первую на B.

Шаг 4

Соедините линию AB и немного растяните ее.

Шаг 5

При том же открытии циркуля и точке на B отметьте точку C.

Шаг 6.

CQ — перпендикуляр к PQ.

Шаг 7.

Расширьте одну сторону сектора, чтобы разрезать CQ в точке E.

Шаг 8

Распределите пополам угол QEP.

Эта биссектриса разрезает QP в точке O.

Шаг 9

Point O — центр круга, вписанного в этот сектор. Теперь круг можно нарисовать, с точкой циркуля на O и открытием, установленным на OQ.

Вот некоторые возможности, в зависимости от количества секторов, в которые был разбит круг. Обратите внимание: круги, которые касаются, дуги между их точками контакта могут быть опущены для создания розетки.

Круг в воздушном змее

Этот метод должен соответствовать числу кругов в полигоне, равному числу сторон этого многоугольника (три круга в треугольнике, пять в пятиугольнике, четыре или восемь в восьмиугольнике . ).

Сначала соедините центр каждой стороны с центром многоугольника, разделив полигон на змеи, а затем выполните следующие действия для каждого змея.

Шаг 1

Bisect ACB. Эта биссектриса разрезает AB на O.

O — центр нашей вписанной окружности, но чтобы точно определить радиус круга, нам нужно найти точку F на AD так, чтобы OF перпендикулярно AD. Это цель остальных шагов:

Шаг 2

Когда черновая точка на A и циркуль открыты для AO, нарисуйте дугу.

Шаг 3

Переместите черновую точку в D и повторите, чтобы найти точку E.

Шаг 4

Соедините к OE, чтобы разрезать AD на F.

Шаг 5

Вписанная окружность теперь может быть нарисована с центром O и радиусом OF.

Как и в предыдущей конструкции, разные полигоны приведут к разным формам, а внутренние дуги могут быть стерты для создания розетки.

Окно Трискеле (три круга)

Такие церковные окна, выдающие кельтское влияние, могут быть замечены во многих местах вокруг Британских островов.

Шаг 1

Начните с круга. Разделите его на шесть и нарисуйте диаметры.

Шаг 2

Соедините три из этих точек, чтобы создать равносторонний треугольник.

Шаг 3

С открытием циркуля ниже нарисуйте круг, вписанный в треугольник.

Шаг 4

Нарисуйте еще один треугольник, вписанный в этот круг.

Шаг 5

С раскрытием компаса ниже, нарисуйте три окружности, центрированные в точках треугольника.

Шаг 6.

С раскрытием циркуля ниже нарисуйте круг, в который вписаны три меньших.

Если вам просто нужен линейный рендеринг, вы можете остановиться здесь и покрасить следующие дуги:

Чтобы нарисовать узор окна, то есть дать этим линиям их собственную толщину и детализировать (где «линия», являющаяся оконной рамкой, имеет собственную толщину и детали), продолжайте .

Шаг 7.

Поместите черновую точку, где находится одно из пересечений диаметра с последним кругом, который мы нарисовали, и установите отверстие на разницу между двумя большими кругами. Нарисуйте небольшой круг.

Шаг 8

Верните сухую точку в исходный центр и откройте ее, как показано. Нарисуйте третий, самый внутренний большой круг.

Шаг 9

Теперь для каждого из трех кругов нарисуйте внутренний круг, используя отверстие, показанное ниже.

Шаг 10

Теперь измените отверстие, как показано, и для каждого из трех, нарисуйте эту дугу:

Шаг 11

Теперь вы можете чертить два внешних круга .

. тогда внутренние капли .

. и, наконец, центральные линии трискеле.

Окно Розетки (Восемь Кругов)

Это окно с западного фасада Шартрского собора и старейшее в здании.

Шаг 1

Начните с большого круга. Разделите его на восемь, выполнив шаги для рисования квадрата (нет необходимости рисовать сам квадрат, потому что нам нужны только его диагонали).

Шаг 2

Разделите половину секторов пополам, чтобы разделить круг на 16.

В настоящее время существует восемь диаметров. Число пунктов для ясности.

Шаг 3

Соедините точки с четными номерами, чтобы создать статический восьмиугольник.

Шаг 4

Стороны восьмиугольника разрезали диаметры в восьми точках. Соедините их, чтобы создать вписанный динамический восьмиугольник.

Шаг 5

Теперь нарисуйте еще один статический восьмиугольник, вписанный в предыдущий.

Шаг 6.

Теперь, возвращаясь к пронумерованным точкам, соедините следующие пары: 2-8 и 10-16, затем 4-14 и 6-12.

Шаг 7.

Соедините 2-12 и 4-10, и, наконец, 6-16 и 8-14.

Обратите внимание на следующие места, где пересекаются три линии: это центры восьми кругов, образующих розетку.

Шаг 8

С открытием циркуля ниже нарисуйте круг, центрированный по каждой из этих точек.

Покажите дуги, показанные здесь.

Шаг 9

Измените открытие циркуля, как показано здесь, и повторите. Нет необходимости рисовать полные круги — вы можете остановить дуги, где они соответствуют диаметру, и закрасить их таким образом.

Шаг 10

Измените отверстие циркуля еще раз и повторите, снова останавливаясь на диаметре.

Шаг 11

Соедините открытые концы дуг.

Шаг 12.

Чертим линии между дугами; Они являются частями диаметров.

Шаг 13.

С последней настройкой циркуля, нарисуйте и закрасьте круг ниже.

Шаг 14.

Наконец, чертим на внешнем круге.

В этой главе о кругах мы закончили основную часть этих уроков по геометрическим проектам. Со следующего месяца мы сосредоточимся на полных моделях и мотивах все более сложной с Востока и Запада.

Видео:Определение центра дуги окружности, построение окружности по 3 точкамСкачать

Спираль архимеда построение формула

Первый ученый который открыл и изучил свойства этой линии, был великий математик и философ из древней Греции, Архимед. Его именем она и была названа.

Видео:Уравнение окружности (1)Скачать

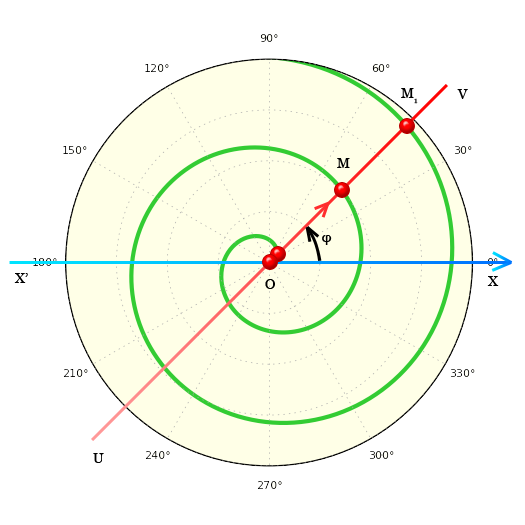
Построение спирали Архимеда

Некоторая прямая UV изначально совпадает с прямой XX`. Прямая UV равномерно вращается относительно точки O. По прямой UV равномерно перемещается точка M отдаляясь от точки O. В результате точка M, перемещаясь по вышеуказанным правилам, описывает линию — спираль Архимеда.

Видео:Найти центр и радиус окружностиСкачать

Шаг спирали Архимеда

При повороте прямой UV из любого положения на некоторый угол Δφ точка M смещается на расстояние Δρ. Смещение MM₁ происходит за один оборот прямой UV, и всегда равно одному и тому же числу. Это число называется шагом спирали Архимеда

Видео:Как начертить золотую спиральСкачать

Полярное уравнение спирали Архимеда

В этом уравнении можно перейти от шага спирали Архимеда a к параметру спирали Архимеда k

Тогда уравнение спирали примет вид

При повороте прямой UV на один радиан, точка M смещается на расстояние равное Параметру спирали Архимеда.

Архимедова спираль – плоская кривая сформированная траекторией произвольной точки, которая размеренно двигается по лучу берущему свое начало в O, одновременно с этим сам луч размерено обращается вокруг O. Перефразировав получаем, расстояние ρ пропорционально углу оборота φ луча. Обороту луча на одинаковый угол соответствует одно и то же увеличение ρ.

Уравнение, характеризующее Архимедову спираль, в полярной системе координат:

где k – сдвиг точки M по лучу r, при обороте на угол, который равен одному радиану.

Обороту прямой на 2π соответствует смещение a = 2kπ.

Число a – шаг спирали.

На основании этого уравнение Архимедовой спирали можно представить таким образом:

Когда поворачиваем луч против движения часовой стрелки, получаем правую спираль, когда поворачиваем – по часовой стрелке – левую спираль. При положительной величине φ формируется правая спираль, отрицательной – левая спираль.

Спирали Архимеда широко используются при построении геометрий для катушек индуктивности, спиральных теплообменников и микрогидродинамических устройств. В этой заметке мы покажем, как построить спираль Архимеда, используя аналитические выражения и их производные для задания необходимых кривых. Сначала мы создадим двухмерную геометрию, а затем, задав нужную толщину, преобразуем её в трёхмерную с помощью операции Extrude (Вытягивание).

Что такое спираль Архимеда?

Широко распространённые в природе спирали или завитки используются во многих инженерных конструкциях. Например, в электротехнике и электронике с помощью проводников спиралевидной формы наматывают катушки индуктивности или проектируют геликоидные антенны. В машиностроении спирали используются при проектировании пружин, косозубых цилиндрических передач или даже механизмов часов, один из которых изображён ниже.

Пример спирали Архимеда, которая используется в часовом механизме. Изображение представлено Greubel Forsey. Доступно по лицензии CC BY-SA 3.0 из Wikimedia Commons.

В данной статье мы разберём только один вид спирали, а именно, спираль Архимеда, которая изображена в механизме выше. Спираль Архимеда – это особый вид спирали с постоянным расстоянием между витками. Благодаря этому свойству она широко распространена при проектировании катушек и пружин.

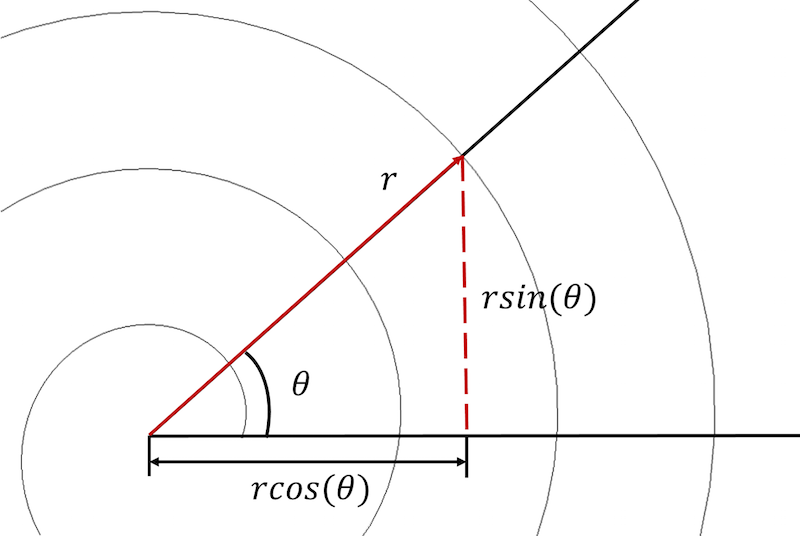
Уравнение спирали Архимеда в полярной системе координат записывается, как:

где a и b — параметры, определяющие начальный радиус спирали и расстояние между витками, которое равно 2 pi b . Обратите внимание, что спираль Архимеда также иногда называют арифметической спиралью. Это имя связывают с арифметической зависимостью расстояния от начала кривой до точек спирали, находящихся на одной радиальной линии.

Задание параметризированной геометрии спирали Архимеда

Теперь, когда вы уже знаете, что такое спираль Архимеда, давайте приступим к параметризации и созданию геометрии в COMSOL Multiphysics.

Спираль Архимеда может быть задана как в полярных, так и в декартовых координатах.

Для начала необходимо преобразовать уравнение спирали из полярной системы координат в декартову и выразить каждое уравнение в параметрической форме:

После преобразования уравнения спирали в параметрической форме в декартовой системе координат примут вид:

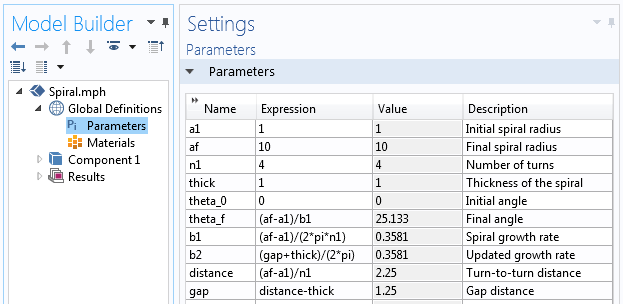
В COMSOL Multiphysics необходимо определить набор параметров, с помощью которых будем задавать геометрию спирали. В нашем случае — это начальный и конечный радиусы спирали a_ и a_ , соответственно, и количество витков n . Показатель роста спирали b находится, как:

Также необходимо определить начальный и конечный углы спирали — theta_0 и theta_f , соответственно. Давайте с них и начнём — theta_0=0 и theta_f=2 pi n . Исходя из заданной информации, определяем параметры для построения геометрии спирали.

Параметры, которые используются для построения геометрии спирали.

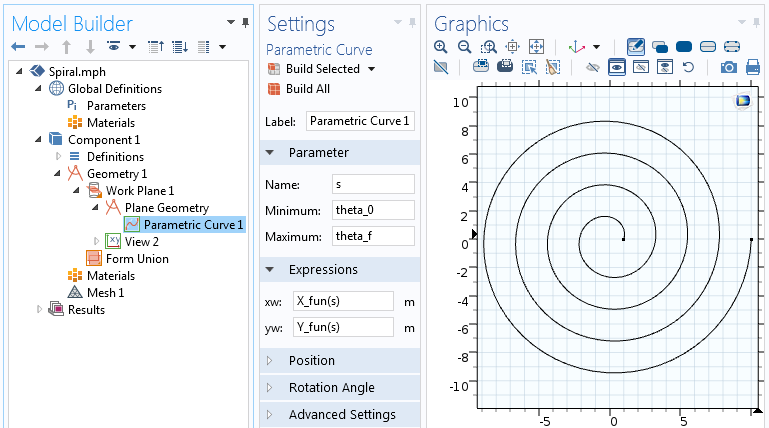
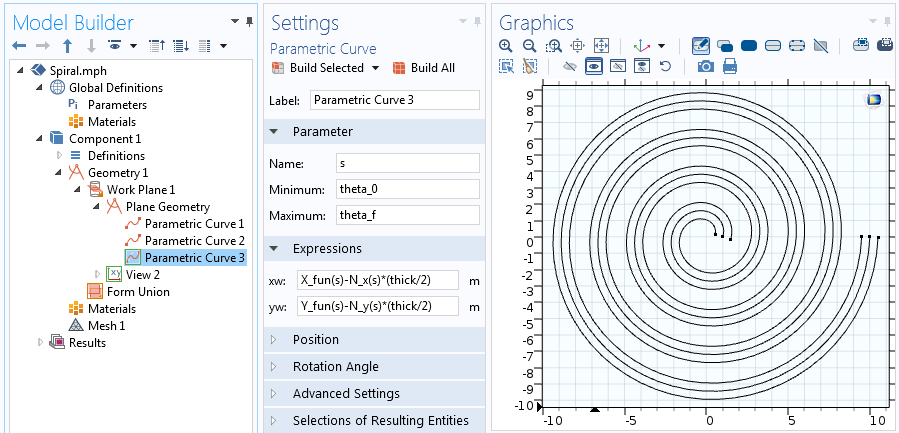
Начнём наше построение, выбрав трёхмерную задачу (3D Component) и создадим Work Plane (Рабочую плоскость) в разделе Geometry (Геометрия). В геометрии для Work Plane добавляем Parametric Curve (Параметрическую кривую) и записываем параметрические уравнения, описанные выше, чтобы задать двухмерную геометрию спирали Архимеда. Данные уравнения можно сразу вписать в соответствующие поля во вкладке Expression либо сначала можно задать каждое уравнение отдельной Аналитической функцией (Analytic function):

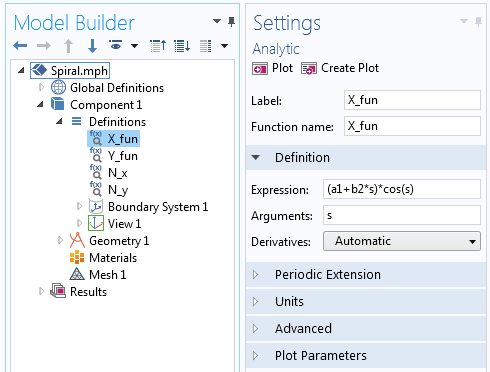
Выражение для X-компоненты уравнения спирали Архимеда, заданное аналитической функцией.

Аналитическая функция затем может использоваться в качестве выражения в узле Parametric Curve. Во вкладке Parameter задаём параметр s от начального угла, theta_0 , до его конечного значения, theta_f=2 pi n .

Настройки для Parametric Curve (Параметрической кривой).

Как только вы зададите все параметры и нажмёте на кнопку «Build Selected», будет построена кривая, изображённая на скриншоте выше. Теперь давайте зададим толщину спирали, чтобы получить твёрдотельную (solid) двухмерную фигуру.

До этого момента параметрами нашей кривой были начальный ( a_ ) и конечный ( a_ ) радиусы и количество витков n . Теперь мы хотим добавить ещё один – толщину спирали.

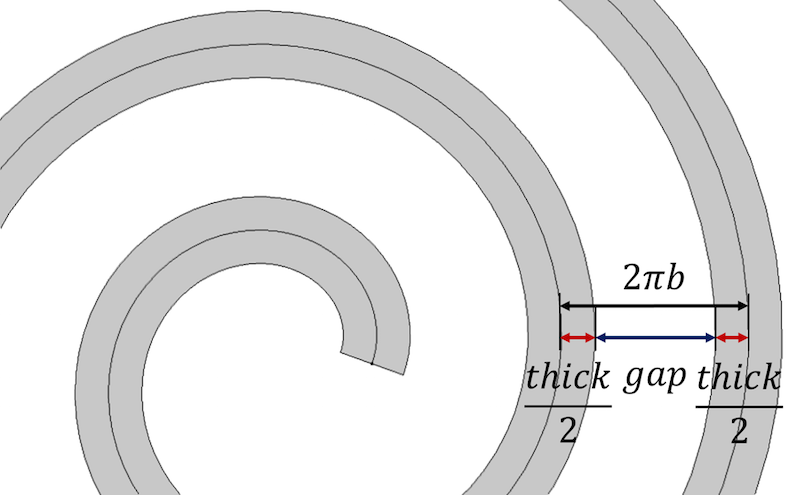
Ещё раз напомним главное свойство спирали — расстояние между витками постоянно и равно 2 pi b . Что эквивалентно frac -a_ > . Чтобы добавить толщину в наши уравнения, представляем расстояние между витками суммой толщины спирали и зазора thick+gap .

Расстояние между витками определяется толщиной спирали и величиной зазора.

Чтобы ввести параметр толщины и сохранить постоянное расстояние между витками, последнее перепишем, как:

После этого выражаем показатель роста спирали через толщину:

Также нужно выразить конечный угол спирали через начальный угол и конечный радиус:

Хотите задать отличный от нуля начальный угол спирали? Если так, то его надо будет добавить в выражение для определения конечного угла: theta_f=frac -a_ >+theta_0 .

Дублирование кривой спирали дважды со смещением на -frac и +frac

по отношению к начальной кривой позволяет построить спираль заданной толщины. Чтобы правильно расположить внутреннюю и внешнюю спирали, необходимо убедиться, что начала данных кривых перпендикулярны линии, на которой расположены их начальные точки. Это можно сделать, домножив расстояние смещения pmfrac

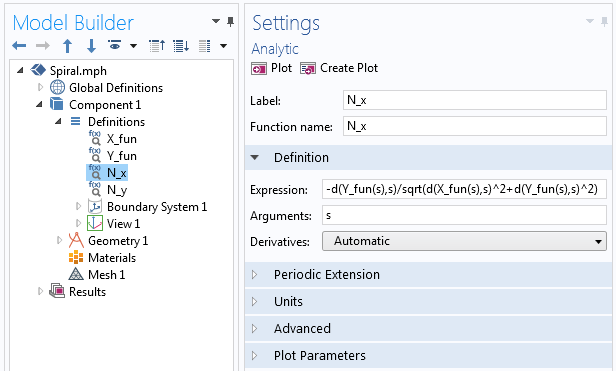
на единичный вектор, расположенный по нормали к начальной кривой спирали. Уравнения векторов нормали в параметрическом виде:

где s — это параметр, используемый в узле Parametric Curve. Чтобы получить нормированные единичные вектора, необходимо эти выражения разделить на длину нормали:

Обновленные параметрические уравнения спирали Архимеда со смещением:

Записывать такие длинные выражения довольно неудобно, поэтому введём следующие обозначения:

где N_x и N_y определяются аналитическими функциями в COMSOL Multiphysics, аналогично X_ и Y_ в первом примере. Внутри функции используется оператор производной, d(f(x),x) , как показано на скриншоте ниже.

Примеры оператора производной, который используется в аналитической функции

Функции X_ , Y_ , N_x , и N_y могут быть использованы в выражениях для задания параметрической кривой, как с одной стороны:

Выражения для второй смещённой параметрической кривой.

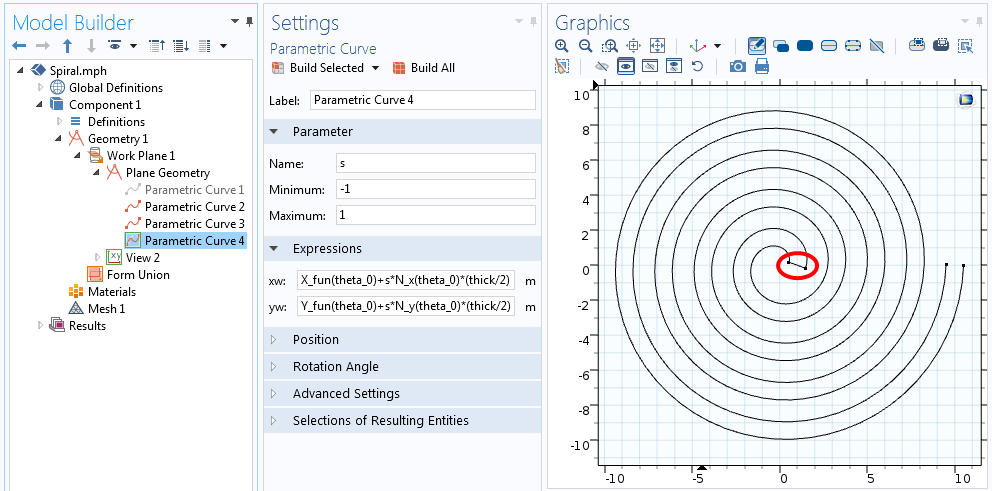
Чтобы соединить концы, добавим ещё две параметрические кривые, используя незначительные изменения уравнений выше. Для кривой, которая будет соединять спираль в центре, необходимо задать X_ , Y_ , N_x , и N_y для начального значения угла, theta. Для кривой, которая будет соединять концы, необходимо задать конечное значение theta. Исходя из этого, уравнения кривой в центре:

Уравнения кривой на конце:

В этих уравнениях параметр s изменяется от -1 до 1, как показано на скриншоте ниже.

Уравнения кривой, соединяющей спираль в центре.

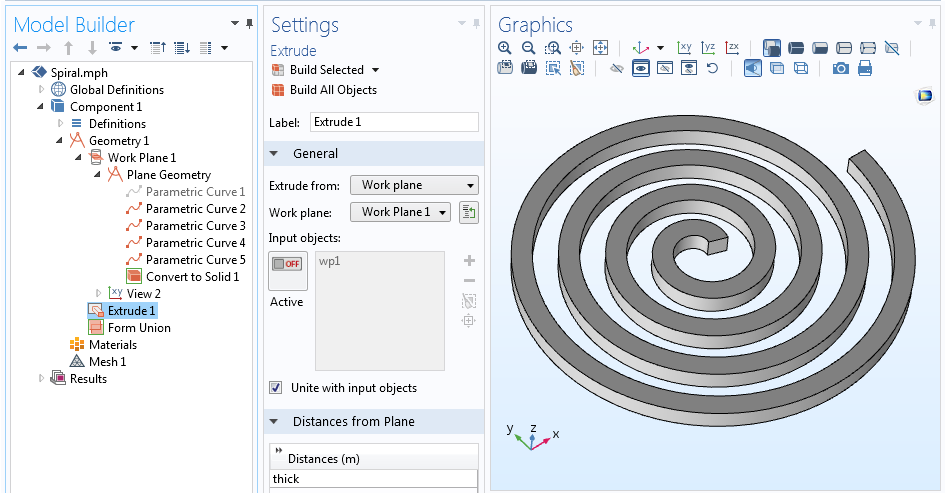
В итоге, мы имеем пять кривых, которые определяют осевую линию спирали и её четыре стороны. Осевую линию можно отключить (функция disable) или даже удалить, так как она не является необходимой. Добавив узел Convert to Solid, создаём единый геометрический объект. Последним шагом является вытягивание данного профиля с помощью операции Extrude и создание трёхмерного объекта.

Полная геометрическая последовательность и вытянутая (экструдированная) трёхмерная геометрия спирали.

Краткие выводы по моделированию спирали Архимеда в COMSOL Multiphysics

В данной заметке мы разобрали основные шаги по созданию параметрической спирали Архимеда. С помощью данной модели вы можете сами экспериментировать с различными значениями параметров, а также попробовать решить с использованием данной параметризации оптимизационную задачу. Надеемся, что данная статья оказалась полезной и вы будете применять данную технику в своих последующих моделях.

📸 Видео

Как найти центр круга в мастерской (4 способа)Скачать

начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

4. Дифракция Френеля. Спираль Френеля.Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Как начертить спиральСкачать

Строим Числовую спиральСкачать

Числовая спираль в ГеогебреСкачать

Построение окружности по трём точкам.Скачать

Как найти центр окружности с помощью циркуля и линейкиСкачать