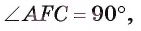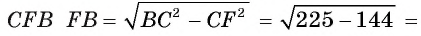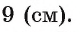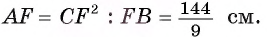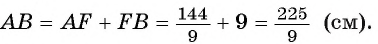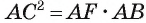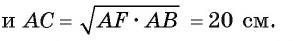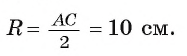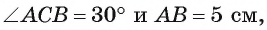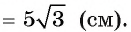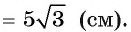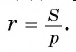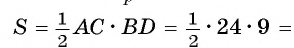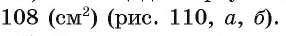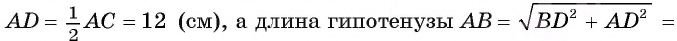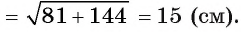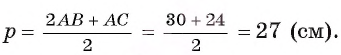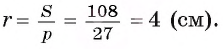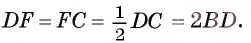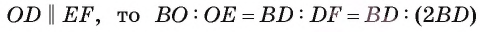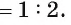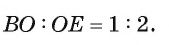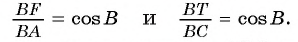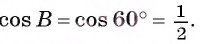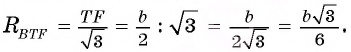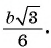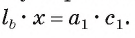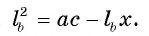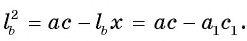Задачи на тему окружность описанная около треугольника

Боковая сторона равнобедренного треугольника равна 4. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника.

Воспользуемся теоремой косинусов:

(здесь a и b — боковые стороны равнобедренного треугольника, c — основание.

Диаметр описанной окружности найдем по обобщенной теореме синусов:

Вместо того, чтобы искать основание треугольника, можно было найти угол при основании. Действительно, сумма углов при основании данного равнобедренного треугольника равна 60°. Эти углы равны, поэтому каждый из них равен 30°. Применяя обобщенную теорему синусов для боковой стороны и противолежащего ей угла, получаем:

Приведем решение Андрея Ларионова.

Угол при основании равен

Следовательно, дуга описанной окружности, на которую он опирается, равна 2 · 30° = 60°. Эту дугу стягивает боковая сторона треугольника.

Хорда, стягивающая дугу в 60°, равна радиусу окружности, поэтому радиус описанной окружности равен боковой стороне треугольника, тогда D = 2 · 4 = 8.

Видео:РЕШЕНИЕ ЗАДАЧИ ПО ТЕМЕ «ОКРУЖНОСТЬ, ОПИСАННАЯ ОКОЛО ТРЕУГОЛЬНИКА». Задачи | ГЕОМЕТРИЯ 7 классСкачать

Решение задач. Окружность, описанная около треугольника 7 класс

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся

Сертификат и скидка на обучение каждому участнику

Урок № 61 Тема: Решение задач Дата _______

научить применять полученные знания на практике, закрепить умения и навыки в процессе решения задач;

способствовать совершенствованию умения работы с чертежными инструментами, учебником;

формировать культуру решения задач, совершенствовать навыки общения.

Цель: создать условия для применения полученных знаний на практике, более глубокого усвоения знаний.

Оборудование, наглядные пособия: циркуль, линейка, доска, учебник, карточки с дидактическим материалом.

Тип урока: урок закрепления знаний, умений и навыков с элементами письменного контроля.

Методы: репродуктивные, практические

Проверка домашней работы

Актуализация учебного процесса (фронтальный опрос)

Определение. Окружность называется описанной около треугольника, если она проходит через все его вершины.

Теорема. Центр окружности, описанной около треугольника, является точкой пересечения перпендикуляров к сторонам треугольника, проведенных через середины этих сторон.

Определение. Окружность называется вписанной в треугольник, если она касается всех его сторон.

Теорема. Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис.

Практические задания (работа в группах).

С помощью шаблонов начертите окружность и «на глаз» постройте ее центр. Попробуйте пояснить методы нахождения места центра окружности (в случае, если центр не указан).

Начертите окружность с центром в точке О. На окружности отметьте три точки А, В, С. Проведите хорды АВ, ВС, СА. Как расположена окружность относительно Δ АВС?

Начертите окружность с центром в точке О. Проведите любые три прямые – касательные к окружности так, чтобы три касательные пересекались. Точки пересечения обозначьте буквами D,E,F. Как расположена окружность относительно Δ DEF?

Окружность, описанная около треугольника и вписанная в треугольник

Подведение итогов урока. Задание на дом

Глава III, § 1.2, 1.3, № (стр. 66-68) (А.Н. Шыныбеков Геометрия – 7)

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 945 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 679 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 302 человека из 66 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 507 751 материал в базе

Материал подходит для УМК

«Геометрия», Погорелов А.В.

39. Окружность, описанная около треугольника

Другие материалы

• 30.10.2018
• 1344
• 9

• 30.10.2018
• 935
• 27

• 29.10.2018
• 1539
• 33

• 29.10.2018
• 664
• 2

• 29.10.2018
• 1678
• 32

• 28.10.2018
• 270
• 0

• 28.10.2018
• 419
• 6

• 28.10.2018
• 687
• 2

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 30.10.2018 3674
• DOCX 204 кбайт
• 79 скачиваний
• Рейтинг: 5 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Малюков Андрей Николаевич. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 6 лет и 6 месяцев
• Подписчики: 1
• Всего просмотров: 25146
• Всего материалов: 17

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Минпросвещения намерено решить вопрос с третьей сменой в школах в 2023 году

Время чтения: 1 минута

Школы Северной Осетии переведут на дистанционное обучение

Время чтения: 1 минута

В Петербурге открыли памятник работавшим во время блокады учителям

Время чтения: 1 минута

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

Минобрнауки запускает конкурс студенческих научных обществ

Время чтения: 1 минута

День памяти жертв холокоста включен в примерный план воспитательной работы

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Треугольники и окружность — задачи с примерами решения

Пример:

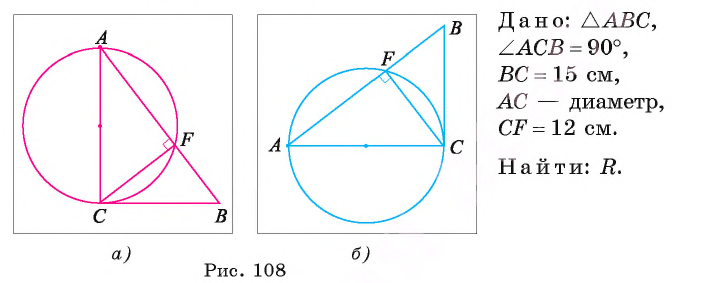
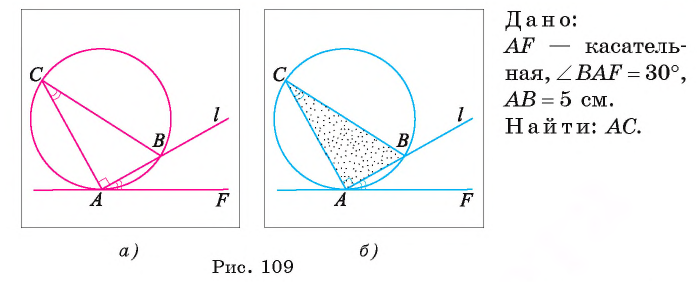
Длина катета ВС прямоугольного треугольника АСВ равна 15 см, а его катет АС является диаметром окружности, которая пересекает гипотенузу в точке F, CF =12 см. Вычислите радиус окружности.

Решение:

Из условия следует, что радиус R равен половине катета АС. Заметим, что

1) В треугольнике

2) Воспользовавшись равенством 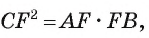найдем

3) Теперь

4) Квадрат длины катета прямоугольного треугольника равен произведению длины гипотенузы и длины проекции этого катета на гипотенузу, следовательно,

Таким образом,

Пример:

Решение:

По теореме об угле между хордой и касательной 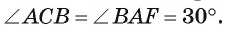Так как точки С и В диаметрально противоположные, то угол САВ опирается на диаметр, а следовательно, он прямой, т. е. треугольник САВ — прямоугольный (рис. 109, а, б). Расстояние от точки С до точки касания А равно длине катета СА треугольника САВ. Так как

Ответ

Пример:

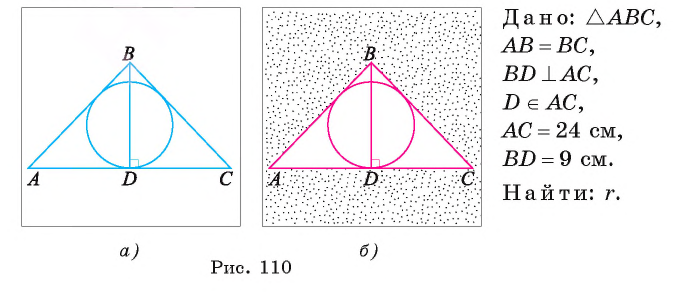
Вычислите радиус окружности, вписанной в равнобедренный треугольник ABC, если длина его основания АС равна 24 см, а высота BD, проведенная к основанию, равна 9 см.

Решение:

Для вычисления радиуса г вписанной окружности воспользуемся формулой 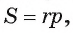где S — площадь треугольника, р — его полупериметр. Отсюда получим

1) Площадь треугольника

2) В прямоугольном треугольнике ADB длина катета

3) Теперь полупериметр

4) Таким образом, найдем

Пример:

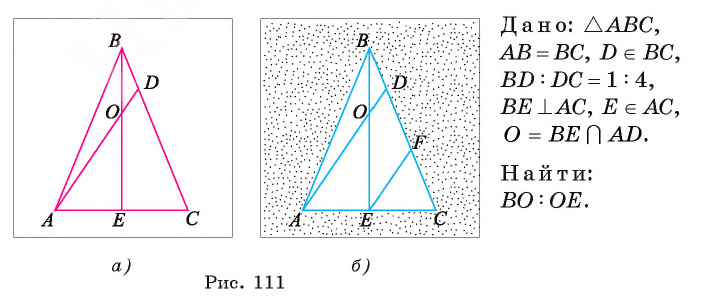
В равнобедренном треугольнике ABC с основанием АС на стороне ВС лежит точка D так, что 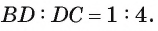В каком отношении точка О пересечения отрезка AD и высоты BE делит высоту BE, считая от вершины В?

Решение:

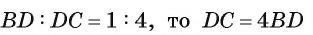
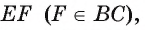
1) Так как (рис. 111, а, б). Проведем отрезок , параллельный отрезку AD.

2) Так как высота, проведенная к основанию равнобедренного треугольника, является медианой, то точка Е — середина стороны АС.

3) По признаку средней линии отрезок EF — средняя линия треугольника ADC, значит,

4) Так как

Ответ:

Пример:

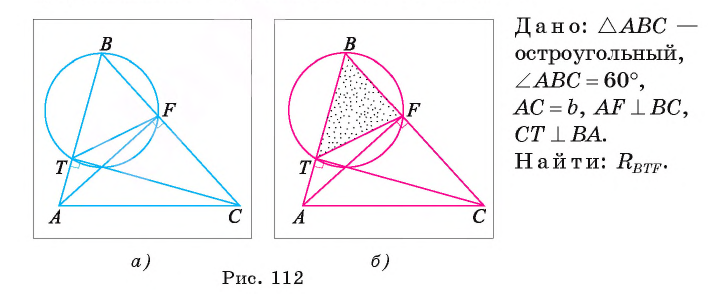
Отрезки AF и СТ — высоты остроугольного треугольника ABC. Найдите радиус окружности, описанной около треугольника BTF, если A ABC = 60° и АС = b.

Решение:

Воспользуемся теоремой синусов и тем, что треугольник ABC подобен треугольнику BTF.

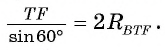
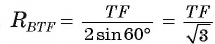
1) В треугольнике BTF по теореме синусов выполняется равенствоСледовательно, (рис. 112, a, 6).

2) Рассмотрим треугольники ABC и FTC. Эти треугольники подобны. Действительно,

Следовательно,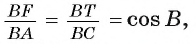т.е. треугольники подобны с коэффициентом подобия

3) Из подобия треугольников ABC и FTC следует, что 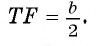Таким образом,

Ответ:

Пример:

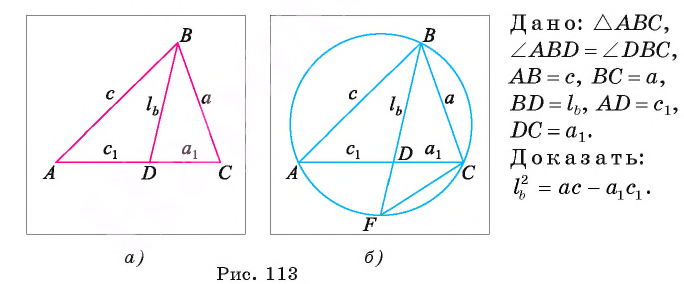
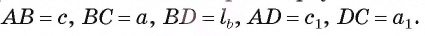
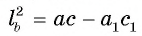
Отрезок BD — биссектриса треугольника ABC. Известно, что Докажите, что (рис. 113, а).

Рассмотрим окружность, описанную около треугольника ABC. Пусть прямая BD пересекает окружность в точке F и DF = х (рис. 113, б).

1) По свойству отрезков пересекающихся хорд выполняется равенство

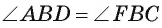
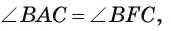
2) Треугольники ABD и FBC подобны, так как по условию и поскольку являются вписанными в окружность и опираются на одну и ту же дугу.

3) Из подобия треугольников ABD и FBC следует, что 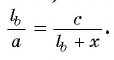Отсюда

3) Таким образом,

Что и требовалось доказать.

• Площадь треугольника
• Соотношения между сторонами и углами произвольного треугольника
• Окружность и круг
• Описанные и вписанные окружности
• Пространственные фигуры — виды, изображения, свойства
• Взаимное расположения прямых на плоскости
• Треугольник
• Решение треугольников

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

🎦 Видео

Построить описанную окружность (Задача 1)Скачать

ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать

Вписанная и описанная окружность - от bezbotvyСкачать

9 класс, 22 урок, Окружность, описанная около правильного многоугольникаСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

8 класс, 39 урок, Описанная окружностьСкачать

ОКРУЖНОСТЬ ОПИСАННАЯ ОКОЛО ТРЕУГОЛЬНИКА радиус 8 классСкачать

Вписанная и описанная окружности. ЗадачиСкачать

ОКРУЖНОСТЬ, ОПИСАННАЯ ОКОЛО ТРЕУГОЛЬНИКА. Видеоурок | ГЕОМЕТРИЯ 7 классСкачать

7 класс. Геометрия. Окружность вписанная в треугольник и окружность описанная около треугольника #11Скачать

Окружность, описанная вокруг треугольника | МатематикаСкачать

7 класс. Окружность, описанная около треугольникаСкачать

Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Задание 24 ОГЭ по математике #7Скачать