Соответственные углы равны 65 то эти две прямые параллельны

Видео:ГЕОМЕТРИЯ 7 класс : Соответственные, односторонние и накрест лежащие углыСкачать

1. Если при пересечении двух прямых третьей прямой соответственные углы равны 65 , то эти две прямые параллельны?

Геометрия | 5 — 9 классы

1. Если при пересечении двух прямых третьей прямой соответственные углы равны 65 , то эти две прямые параллельны.

2. Любые две прямые имеют не менее одной общей точки.

3. Через любую точку проходит более одной прямой.

4. Любые три прямые имеют не менее одной общей точки.

1. ) Соответственные углы в сумме дают 180 градусов.

Соответственно данные прямые не параллельны.

2. ) Две прямые могут быть параллельны и тогда у них не будет не одной общей точки.

3. ) Через любую точку проходит более одной прямой) +

) Три прямые могут быть параллельны и тогда у них не будет не одной общей точки.

Видео:Теорема 14.1 Если накрест лежащие углы равны, то прямые параллельныСкачать

Укажите номера верных утверждений?

Укажите номера верных утверждений.

1) Любые две прямые имеют не менее одной общей точки.

2) Если две прямые перпендикулярны третьей прямой, то эти две прямые

3) Если угол равен 38° , то смежный с ним равен 142° .

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Две прямые , перпендикулярные третьей прямой , имеют одну точку пересечения?

Две прямые , перпендикулярные третьей прямой , имеют одну точку пересечения?

Видео:7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать

Какие из следующих утверждений верны : 1?

Какие из следующих утверждений верны : 1.

Если при пересечении двух прямых третьей прямой соответственные углы равны 65 градусов, то эти две прямые параллельны.

2. Любые две прямые имеют не менее одной общей точки.

3. Через любую точку проходит более одной прямой.

4. Любые три прямые имеют не менее одной общей точки.

Видео:ГЕОМЕТРИЯ 7 класс. Признаки параллельности, накрест лежащие, соответственные и односторонние углыСкачать

Какие из следующих утверждений верны?

Какие из следующих утверждений верны?

1) через любые три точки проходит равно одна прямая.

2) сумма смежных угла равна 90 градусов.

3)Если при пересечении двух прямых третьей прямой соответственные углы составляют в сумме 180 градусов , то эти две прямые параллельны.

4) через любые две точки проходит не более одной прямой.

Видео:Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать

Какие ответы верны?

Какие ответы верны?

1. Если при пересечении двух прямых третьей прямой соответственные углы равны 65 , то эти две прямые параллельны.

 2. Любые две прямые имеют не менее одной общей точки.

3. Через любую точку проходит более одной прямой.

4. Любые три прямые имеют не менее одной общей точки.

Видео:7 класс, 25 урок, Признаки параллельности двух прямыхСкачать

1) Сколько прямых, параллельных данной прямой проходит через точку не принадлежащую прямой?

1) Сколько прямых, параллельных данной прямой проходит через точку не принадлежащую прямой?

2) Сколько общих точек имеют две прямые?

3) Сколько общих точек имеют три прямые?

4) Сколько прямые проходит через любые три точки?

5) Сколько прямых проходит через одну точку?

Видео:7 класс, 30 урок, Углы с соответственно параллельными или перпендикулярными сторонамиСкачать

Укажите номера верных утверждений 1) Через любую точку проходит не менее одной прямой 2) Если при пересечении двух прямых третьей прямой соответственные углы равны 65градусам, то эти две прямые паралл?

Укажите номера верных утверждений 1) Через любую точку проходит не менее одной прямой 2) Если при пересечении двух прямых третьей прямой соответственные углы равны 65градусам, то эти две прямые параллельны 3) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90 градусов, то эти две прямые параллельны.

Видео:SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать

Какие из следущих утверждений верны?

Какие из следущих утверждений верны?

1)любые три прямые имеют не более одной общей точки.

2)через любую точку проходит более одной прямой.

3)если две прямые пепендикулярны третьей прямой, то эти де прямые пепендикулярны.

Видео:Пары углов в геометрииСкачать

Какие из следующих утверждений верны?

Какие из следующих утверждений верны?

1) Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны.

2) Любые две прямые имеют не менее одной общей точки.

3) Через любую точку проходит более одной прямой.

Видео:Параллельные прямые (задачи).Скачать

Какие из следующих утверждений верны?

Какие из следующих утверждений верны?

1) Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны.

2) Любые две прямые имеют не менее одной общей точки.

3) Через любую точку проходит более одной прямой.

На этой странице сайта, в категории Геометрия размещен ответ на вопрос 1. Если при пересечении двух прямых третьей прямой соответственные углы равны 65 , то эти две прямые параллельны?. По уровню сложности вопрос рассчитан на учащихся 5 — 9 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.

Координаты вектора АВ будет [1 ; — 3], так как : ( — 3) + 4 = 1, а ( — 2) + ( — 1) = — 3.

Видео:Параллельные прямые — Признак Параллельности Прямых и Свойства УгловСкачать

Соответственные углы равны 65 то эти две прямые параллельны

Какие из следующих утверждений верны?

1) Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны.

2) Любые две прямые имеют не менее одной общей точки.

3) Через любую точку проходит более одной прямой.

4) Любые три прямые имеют не менее одной общей точки.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны.» — верно, так как если соответственные углы равны, то прямые параллельны.

2) «Любые две прямые имеют не менее одной общей точки.» — неверно, две прямые имеют не более одной общей точки.

3) «Через любую точку проходит более одной прямой.» — верно, через одну точку проходит множество пересекающихся в этой точке прямых.

4) «Любые три прямые имеют не менее одной общей точки.» — неверно, любые три прямые, которые не совпадают, если и имеют общую точку, то только одну.

Видео:Диагностическая работа в формате ОГЭ. Задача-13Скачать

Параллельные прямые. Признаки параллельности прямых

Как мы знаем, прямые либо пересекаются (т.е. имеют одну общую точку), либо не пересекаются (т.е. не имеют ни одной общей точки).

Определение 1. Две прямые на плоскости называются параллельными , если они не пересекаются.

Если прямые a и b параллельны, то это обозначают так:

.

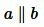На рисунке Рис.1 изображены прямые a и b, которые перпендикулярны к прямой c. В этом случае эти прямые не пересекаются (см. статью Перперндикулярные прямые), т.е. они параллельны (Определение 1).

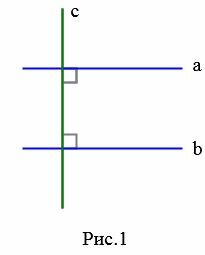Понятие параллельности можно распространять и на отрезки.

Определение 2. Два отрезка называются параллельными , если они лежат на параллельных прямых (Рис.2).

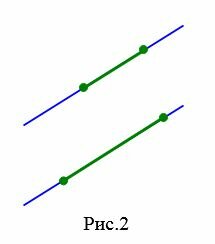Аналогично определяется параллельность отрезка и прямой, отрезка и луча, двух лучей, луча и прямой.

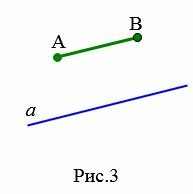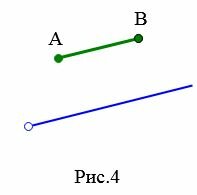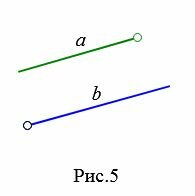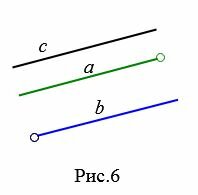На Рис.3 отрезок AB пераллелен к прямой a поскольку прямая, проходящай через отроезок AB параллельна прямой a. На рисунке Рис.4 отрезок AB пераллелен к лучу a так как прямые, проходящие через отрезок AB и луч a параллельны. Для Рис.5 и Рис.6 можно сделать аналогичные рассуждения.

Видео:10 класс, 8 урок, Углы с сонаправленными сторонамиСкачать

Признаки параллельности прямых

Определение 3. Прямая c называется секущей по отношению к прямым a и b, если она пересекает их в двух точках.

При пересечении прямой c с a и b образуются восемь углов, некоторые пары из которых имеют специальные названия (Рис.7):

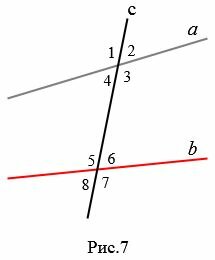• накрест лежащие углы: 3 и 5, 4 и 6;
• односторонние углы: 4 и 5, 3 и 6;
• соответственные углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7.

Определим признаки параллельности двух прямых, связанные с этими парамы углов.

Теорема 1. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

Доказательство. Предположим, что при пересечении прямых a и b секущей AB накрест лежащие углы равны: (Рис.8).

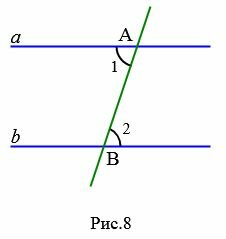Докажем, что .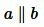

Если углы 1 и 2 прямые (Рис.9), то получается, что прямые a и b перпендикулярны прямой AB и, следовательно, они параллельны (теорема 1 статьи Перперндикулярные прямые и определение 1 настоящей статьи).

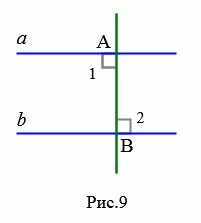Предположим, что углы 1 и 2 не прямые (Рис.10).

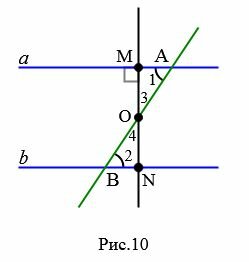Найдем середину отрезка AB и обозначим через O. Из точки O проведем перпендикуляр OM к прямой a. На прямой b отложим отрезок BN равной отрезку MA. Треугольники OAM и OBN равны по двум сторонам и углу между ними, так как OA=OB, MA=NB, . Тогда и .

означает, что точка N лежит на продолжении луча MO, т.е. точки M, O, N лежат на одной прямой. Угол BNO прямой (поскольку угол AMO прямой). Получается, что прямые a и b перпендикулярны к прямой MN, следовательно они параллельны.

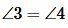
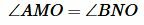
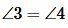
Теорема 2. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Доказательство. Пусть при пересечении прямых a и b секущей с соответственные углы равны, например (Рис.11).

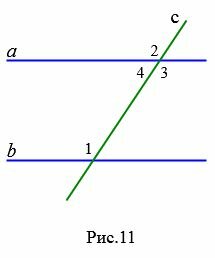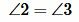
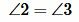
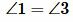
Так как углы 2 и 3 вертикальные, то . Тогда из и следует, что . Но углы 1 и 3 накрест лежащие и, по теореме 1, прямые a и b параллельны.

Теорема 3. Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.

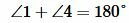
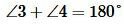
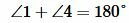
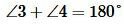
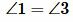
Доказательство. Пусть при пересечении прямых a и b секущей с сумма односторонних углов равна 180°, например (Рис.11). Из рисунка видно, что углы 4 и 3 смежные, т.е. . Из и следует, что . Но углы 1 и 3 накрест лежащие и, по теореме 1 прямые a и b параллельны.

🎬 Видео

Геометрия | 7 класс | Атанасян Л.С. | Номер 215 | Подробный разборСкачать

7 класс, 11 урок, Смежные и вертикальные углыСкачать

29. Теорема об углах, образованных двумя параллельными прямыми и секущейСкачать

Признаки параллельности прямых. Геометрия. 7 КлассСкачать

МЦКО математика 7 класс задание 7 параллельные прямыеСкачать

Геометрия 7 класс. Углы с соответственно параллельными или перпендикулярнымСкачать