Дуги концентрических и эксцентрических окружностей (2 видео)

Картографические проекции

Существуют следующие классификации картографических проекций: по характеру искажений; по виду вспомогательной геометрической поверхности, с помощью которой сеть меридианов и параллелей с эллипсоида переносят на плоскость; по территориальному охвату [11. С. 7].

I. Классификация картографических проекций по характеру искажений

Равноугольные (конформные) проекции сохраняют величину углов, формы бесконечно малых фигур. Масштаб длин в каждой точке постоянен по всем направлениям в зависимости от положения точки. Эллипсы искажений выражаются окружностями различных радиусов (рис. 11, а).

Равновеликие проекции не искажают площади. В этих проекциях площади эллипсов искажений равны. Увеличение масштаба длин по одной оси эллипса искажений компенсируется уменьшением масштаба длин по другой оси, что вызывает сильное искажение форм (рис. 11, в).

Рис. 77. Геометрическое представление искажений:

а — в равноугольной проекции; б — в произвольной (равнопромежуточной) проекции; в — в равновеликой проекции

Произвольные проекции искажают и углы, и площади. Среди них можно выделить равнопромежуточные проекции, во всех точках которых масштаб по одному из направлений, например по меридианам или параллелям, постоянен и равен главному (рис. 11, б).

II. Классификация картографических проекций по виду вспомогательной геометрической поверхности

Различают проекции азимутальные, цилиндрические, конические.

Азимутальные проекции характеризуются тем, что в них сеть меридианов и параллелей переносится с поверхности эллипсоида на касательную (или секущую) плоскость. Изображение около точки касания почти совсем не искажается — это точка нулевых искажений.

А. Азимутальные проекции в зависимости от положения точки касания плоскости на поверхности земного эллипсоида подразделяются [12. С. 8—18]:

1) полярные, или нормальные (рис. 12, а). Вид сетки: меридианы — прямые линии, радиально расходящиеся из полюса, параллели — концентрические окружности с центром в полюсе;
40

2) экваториальные, или поперечные (рис. 12, б). Вид сетки: средний меридиан и экватор — взаимно перпендикулярные прямые, остальные меридианы и параллели — кривые линии. В некоторых случаях параллели изображаются прямыми линиями;
3) горизонтальные, или косые (рис. 12, в). Вид сетки: средний меридиан, на котором расположена точка касания, представляет собой прямую, остальные меридианы и параллели — кривые линии.

Рис 12. Положение касательной плоскости относительно земного эллипсоида и вид картографической сетки в нормальной (а), поперечной (б) и косой (в) азимутальной проекциях

Б. В зависимости от положения центра проектирования в перспективных азимутальных проекциях выделяются:

1) центральные — центр проектирования находится в центре Земли;
2) стереографические — центр проектирования расположен на конце диаметра, противоположном точке касания;
3) ортографические — центр проектирования лежит в бесконечности;
4) внешние — центр проектирования лежит вне поверхности Земли, но на конечном расстоянии (рис. 13).

Азимутальные проекции применяются для территорий, протяженность которых по широте и долготе примерно одинакова; полярная азимутальная — для Северного и Южного полушарий; экваториальные — для Восточного и Западного полушарий, карт Африки; горизонтальные — для карт Азии, Австралии и т. д.

Цилиндрические проекции — проекции, в которых сеть меридианов и параллелей с поверхности эллипсоида переносится на боковую поверхность касательного (или секущего) цилиндра, затем цилиндр разрезается по образующей и развертывается в плоскость (см. рис. 7, 8).

Рис. 13. Перенесение поверхности земного шара на касательную к нему плоскость (Q) в перспективной внешней азимутальной проекции:

О — центр земного шара; Oj — точка касания; К — «точка зрения»

Рис. 14. Положение касательного цилиндра относительно земного эллипсоида (шара) и вид картографической сетки в нормальной (а), поперечной (б) и косой (в) цилиндрической проекциях

В зависимости от ориентировки цилиндра относительно оси земного эллипсоида различают проекции: нормальные, поперечные и косые.

1. Нормальные (рис. 14, а). Вид сетки: меридианы — равноотстоящие параллельные прямые, параллели — прямые, им перпендикулярные. Нормальные цилиндрические проекции применяют для территорий, вытянутых вдоль экватора. Они широко используются для карт мира. В равноугольной нормальной цилиндрической проекции Меркатора создаются морские карты.
2. Поперечные (рис. 14, б). Ось цилиндра лежит в плоскости экватора. Эти проекции применяются для территорий, вытянутых по меридиану.
3. Косые (рис. 14, в). Ось цилиндра составляет с осью эллипсоида острый угол.

В поперечных и косых цилиндрических проекциях меридианы и параллели — кривые линии.

Конические проекции — проекции, в которых сеть меридианов и параллелей с поверхности эллипсоида переносится на боковую поверхность касательного (или секущего) конуса.

Подобно цилиндрическим проекциям конические проекции делятся: на нормальные, поперечные и косые (рис. 15).

Рис. 15. Ориентирование конуса относительно земного эллипсоида (шара) в нормальной (а), поперечной (6) и косой (в) конической проекциях

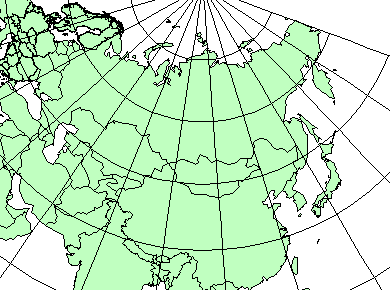
1. Нормальные — ось конуса совпадает с малой осью земного эллипсоида (рис. 15, а). Вид сетки (рис. 16): меридианы — прямые линии, расходящиеся из вершины конуса; параллели — дуги концентрических окружностей. Проекции применяются для территорий, вытянутых по параллелям и лежащих в средних широтах (карты России).
2. Поперечные — ось конуса лежит в плоскости экватора (рис. 15, б).
3. Косые — ось конуса составляет с осью эллипсоида острый угол (рис. 15, в).

Рис. 16. Положение касательного по параллели конуса относительно земного эллипсоида (шара) и вид картографической сетки в нормальной конической проекции

Поперечные и косые конические проекции употребляются очень редко.

Поликонические проекции, в которых сеть меридианов и параллелей с поверхности эллипсоида переносится на боковые поверхности нескольких конусов. Вид сетки: параллели — дуги эксцентрических окружностей, центральный меридиан — прямая линия, все остальные меридианы — кривые линии.

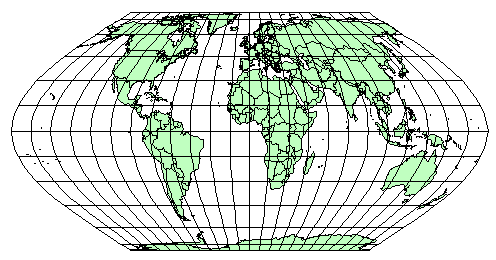
Условные проекции — проекции, при построении которых не используют вспомогательные геометрические поверхности. Сеть меридианов и параллелей строят по какому-нибудь заранее заданному условию. В условных проекциях выделяются псевдоцилиндри- ческие и псевдоконические проекции, сохраняющие от исходных (цилиндрических и конических) проекций вид параллелей. Вид сетки: средний меридиан — прямая линия, остальные меридианы — кривые линии. Условные проекции получили широкое применение.

На рис. 17 приведены виды сеток описанных в этом параграфе картографических проекций. По виду сетки можно определить, в какой проекции создана та или иная географическая карта, даже по ее фрагменту, т. е. определить класс проекции.

Рис. 17. Вид сетки меридианов и параллелей в разных картографических проекциях:

а — цилиндрической; б — конической; в — азимутальной; г — псевдоцилиндрической; д — псевдоконической; е — поликонической; ж — псевдоазимутальной

III. Классификация картографических проекций по территориальному охвату

В этой классификации выделяются картографические проекции:

— для карт мира;
— карт полушарий;
— материков и океанов;
— карт отдельных государств и их частей.

По этому принципу построены таблицы-определители картографических проекций.

Видео:Метод концентрических сфер.Скачать

Классификация проекций по виду нормальной картографической сетки

Азимутальные проекции – этопроекции, в которых параллели изображаются концентрическими окружностями, а меридианы – прямыми, исходящими из общего центра параллелей, под углами, равными разности их долгот (рис. 2.15).

Рис. 2.15. Азимутальная проекция

Конические проекции – этопроекции, в которых параллели изображаются дугами концентрических окружностей, а меридианы – прямыми, расходящимися из общего центра параллелей, под углами, равными разности их долгот (рис. 2.16).

Рис. 2.16. Коническая проекция

Цилиндрические проекции – этопроекции, в которых меридианы изображаются равноотстоящими параллельными прямыми, а параллели перпендикулярными к ним прямыми, в общем случае не равноотстоящими (рис.2.17).

Рис. 2.17. Цилиндрическая проекция

Псевдоазимутальные проекции – этопроекции, в которых параллели изображаются концентрическими окружностями, меридианы – кривыми, сходящимися в точке полюса, средний меридиан – прямой.

Псевдоконические проекции – этопроекции, в которых параллели изображаются дугами концентрических окружностей, средний меридиан – прямой, проходящей через их общий центр, остальные меридианы – кривые.

Псевдоцилиндрические проекции – этопроекции, в которых параллели изображаются параллельными прямыми, средний меридиан – прямая, перпендикулярная к параллелям, остальные меридианы – кривые или прямые, наклоненные к параллелям (рис. 2.18).

Рис. 2.18. Псевдоцилиндрическая проекция

Полиазимутальные проекции – этопроекции, в которых параллели изображаются эксцентрическими окружностями, меридианы – кривые, сходящиеся в точке полюса, средний меридиан – прямой.

Поликонические проекции – этопроекции, в которых параллели изображаются дугами эксцентрических окружностей с радиусами тем большими, чем меньше их широта, средний меридиан – прямой, на которой расположены центры всех параллелей, остальные меридианы – кривые (рис. 2.19).

Видео:Метод эксцентрических сферСкачать

Картографические проекции

При практической работе с картой географ должен хорошо знать математические основы ее построения, уметь определять наиболее распространенные картографические проекции по виду сетки, вычислять размеры искажений географических объектов на картах и вносить поправки в измеренные по картам величины.

Геометрические законы построения и геометрические свойства картографического изображения определяются математической основой, элементами которой являются масштаб, геодезическая основа и картографическая проекция.

Масштаб определяет степень уменьшения длин и площадей.

Геодезическая основа определяет переход от физической поверхности Земли к условной поверхности эллипсоида (или шара), а также обеспечивает правильное положение изображаемых на карте объектов по широте, долготе, высоте.

Картографические проекции – способы условного изображения поверхности Земли (принимая ее за эллипсоид или шар) на плоскости, т. е. картографической сетки, соответствующей географической сетке.

Проекция устанавливает однозначное соответствие между геодезическими координатами широты B и долготы L (или сферическими координатами широты ϕ и долготы л) точек и их прямоугольными координатами X и Y на карте:

X= f1 (B, L) и Y= f2 (B, L) или X = f1 (ϕ, л ) и Y = f2 (ϕ, л )

Конкретные реализации функций f1 и f2 часто выражены довольно сложными математическими зависимостями, их число бесконечно, а, следовательно, разнообразие картографических проекций практически неограниченно. Необходимо лишь, чтобы каждая точка B и L эллипсоида (ϕ, л шара) изображалась на плоскости однозначно соответствующей точкой X и Y и чтобы изображение было непрерывным.

Картографические проекции обычно различают по характеру искажений и по виду вспомогательной геометрической поверхности, с помощью которой сеть меридианов и параллелей с эллипсоида (или шара) переносят на плоскость. Практически ценным является подразделение по территориальному охвату. По территориальному охвату выделяются картографические проекции для карт мира, полушарий, материков и океанов, карт отдельных государств и их частей. По этому принципу построены таблицы-определители картографических проекций.

По характеру искажений проекции делятся на равноугольные, равновеликие и произвольные.

Равноугольные (или конформные) проекции сохраняют величину углов и формы бесконечно малых фигур. Масштаб длин в каждой точке постоянен по всем направлениям (что обеспечивается закономерным увеличением расстояний между соседними параллелями по меридиану) и зависит только от положения точки. Эллипсы искажений выражаются окружностями различных радиусов.

Такие проекции особенно удобны для определения направлений и прокладки маршрутов по заданному азимуту (например, при решении навигационных задач).

Равновеликие (или эквивалентные) проекции не искажают площади. В этих проекциях площади эллипсов искажений равны. Увеличение масштаба длин по одной оси эллипса искажений компенсируется уменьшением масштаба длин по другой оси, что вызывает закономерное уменьшение расстояний между соседними параллелями по меридиану и, как следствие, – сильное искажение форм.

Такие проекции удобны для измерения площадей объектов (что, например, существенно для некоторых экономических или морфометрических карт).

В теории математической картографии доказывается, что нет и не может быть проекции, которая была бы одновременно и равноугольной, и равновеликой. Вообще, чем больше искажения углов, тем меньше искажения площадей и наоборот.

Произвольные проекции искажают и углы, и площади. При их построении стремятся найти наиболее выгодное для каждого конкретного случая распределение искажений, достигая как бы некоторого компромисса; эта группа проекций используется в случаях, когда чрезмерные искажения углов и площадей одинаково нежелательны. По своим свойствам произвольные проекции лежат между равноугольными и равновеликими. Среди них можно выделить равнопромежуточные (или эквидистантные) проекции, во всех точках которых масштаб по одному из главных направлений, обычно по меридианам или параллелям, постоянен и равен главному.

По виду вспомогательной геометрической поверхности различают проекции: цилиндрические, азимутальные и конические.

Цилиндрическими называют проекции, в которых сеть меридианов и параллелей с поверхности эллипсоида переносится на боковую поверхность касательного (или секущего) цилиндра, а затем цилиндр разрезается по образующей и развертывается в плоскость. Искажения минимальны вблизи линии касания или двух линий сечения цилиндра земного эллипсоида, являющихся линиями нулевых искажений.

В зависимости от ориентировки цилиндра относительно оси земного эллипсоида различают проекции:

– нормальные, когда ось цилиндра совпадает с малой осью земного эллипсоида; меридианы в этом случае представляют собой равноотстоящие параллельные прямые, а параллели – прямые, им перпендикулярные;

– поперечные, когда ось цилиндра лежит в плоскости экватора; вид сетки: средний меридиан и экватор – взаимно перпендикулярные прямые, остальные меридианы и параллели – кривые линии;

– косые, когда ось цилиндра составляет с осью эллипсоида острый угол; в косых цилиндрических проекциях меридианы и параллели – кривые линии.

Азимутальными называют проекции, в которых сеть меридианов и параллелей переносится с поверхности эллипсоида на касательную (или секущую) плоскость. Изображение около точки касания (или линии сечения) плоскости земного эллипсоида почти совсем не искажается. Точка касания (или линия сечения) является точкой (линией) нулевых искажений.

В зависимости от положения точки касания плоскости на поверхности земного эллипсоида среди азимутальных проекций различают:

– нормальные, или полярные, когда плоскость касается Земли в одном из полюсов; вид сетки: меридианы – прямые линии, радиально расходящиеся из полюса, параллели – концентрические окружности с центрами в полюсе;

– поперечные, или экваториальные, когда плоскость касается эллипсоида в одной из точек экватора; вид сетки: средний меридиан и экватор – взаимно перпендикулярные прямые, остальные меридианы и параллели – кривые линии (в некоторых случаях параллели изображаются прямыми линиями);

– косые, или горизонтные, когда плоскость касается эллипсоида в какой-либо точке, лежащей между полюсом и экватором. В косых проекциях только средний меридиан, на котором расположена точка касания, представляет собой прямую, остальные меридианы и параллели – кривые линии.

Коническими называются проекции, в которых сеть меридианов и параллелей с поверхности эллипсоида переносится на боковую поверхность касательного (или секущего) конуса. Искажения мало ощутимы вдоль линии касания или двух линий сечения конуса земного эллипсоида, которые являются линией (линиями) нулевых искажений.

Подобно цилиндрическим конические проекции делятся на:

– нормальные, когда ось конуса совпадает с малой осью земного эллипсоида; меридианы в этих проекциях представлены прямыми линиями, расходящимися из вершины конуса, а параллели – дугами концентрических окружностей;

– поперечные, когда ось конуса лежит в плоскости экватора; вид сетки: средний меридиан и параллель касания – взаимно перпендикулярные прямые, остальные меридианы и параллели – кривые линии;

– косые, когда ось конуса составляет с осью эллипсоида острый угол; в косых конических проекциях меридианы и параллели – кривые линии.

В нормальных цилиндрических, азимутальных и конических проекциях картографическая сетка ортогональна – меридианы и параллели пересекаются под прямыми углами, что является одним из важных диагностических признаков этих проекций.

Поликоническими называются проекции, в которых сеть меридианов и параллелей с поверхности эллипсоида переносится на боковые поверхности нескольких конусов, каждый из которых разрезается по образующей и развертывается в плоскость. В поликонических проекциях параллели изображаются дугами эксцентрических окружностей, центральный меридиан представляет собой прямую, все остальные меридианы – кривые линии, симметричные относительно центрального.

Условными называются проекции, при построении которых не прибегают к использованию вспомогательных геометрических поверхностей. Сеть меридианов

и параллелей строят по какому-нибудь заранее заданному условию. Среди условных проекций можно выделить псевдоцилиндрические, псевдоазимутальные и псевдоконические проекции, сохраняющие от исходных цилиндрических, азимутальных

и конических проекций вид параллелей. В этих проекциях средний меридиан – прямая линия, остальные меридианы – кривые линии.

К условным проекциям относятся также многогранные проекции, которые получают путем проектирования на поверхность многогранника, касательного или секущего земной эллипсоид. Каждая грань представляет собой равнобочную трапецию (реже – шестиугольники, квадраты, ромбы). Разновидностью многогранных проекций являются многополосные проекции, причем полосы могут нарезаться и по меридианам, и по параллелям. Такие проекции выгодны тем, что искажения в пределах каждой грани или полосы совсем невелики, поэтому их всегда используют для многолистных карт. Основное неудобство многогранных проекций состоит в невозможности совмещения блока листов карт по общим рамкам без разрывов.

Определение картографических проекций

Цель задания. Изучить наиболее распространенные картографические проекции и уметь их распознавать по виду сетки меридианов и параллелей.

Выполнение задания. Определить картографические проекции географических карт в указанных ниже вариантах (табл. 1).

Исходные (рабочие) материалы. Варианты картографических проекций (прил. 1), альбомный лист, черная гелевая ручка, карандаш, ластик, циркуль-измеритель, линейка, калька.

Указания к выполнению задания.

1. Ознакомиться с таблицами для определения проекций карт мира, полушарий, карт материков и их крупных частей, карт океанов, а также карт бывшего СССР и РФ (табл. 3, 4, 5, 6, 7). Таблицы-определители составлены по единому принципу: в заголовках столбцов формулируются вопросы (условия); последовательно отвечая на них и переходя от левых столбцов к правым, область поиска в пределах строк сужается; в крайнем правом столбце приведено полное название искомой проекции, для которой выполняются все условия внутри соответствующей строки.

2. Ознакомиться с картографическими проекциями предлагаемых географических карт (прил. 1). Для определения проекции выяснить:

– какая территория изображена на карте (мир, полушария, материки, их части, государства, Россия, ее части и др.), и по какой таблице следует проводить определение;

– какова форма рамки географической карты (круглая, прямоугольная, эллиптическая или отсутствует);

– какими линиями изображаются меридианы (прямыми, кривыми) и параллели (прямыми, кривыми, дугами концентрических или эксцентрических окружностей). Прямолинейность линии устанавливается с помощью линейки; для того, чтобы установить, является ли кривая дугою окружности, на листе кальки на расстоянии 3-5 мм друг от друга отмечают три точки этой кривой (рис. 20а); если все три точки при движении листа по кривой будут совпадать с нею, то кривая – дуга окружности (рис. 20б); у концентрических окружностей промежутки между смежными окружностями, измеренные циркулем-измерителем, равны по величине, у эксцентрических вследствие разных радиусов кривизны – изменяются (рис. 20в);

– как изменяются промежутки между параллелями по прямому (среднему) меридиану (равны, увеличиваются или уменьшаются и во сколько раз);

– каковы дополнительные сведения о проекции1 (экватор – прямая или кривая, не изображен; полюс – не изображен, показан точкой и т. д.).

3. По таблице-определителю дать полное название картографической проекции, выяснить вид проекции по характеру искажений.

Результаты работы должны быть представлены в виде таблицы (табл. 2), как показано в приведенном ниже примере выполнения задания.

Рис. 20. Определение дуг окружностей: а) размещение трех точек на листе кальки, принадлежащих линии; б) перемещение листа кальки вдоль линии и нахождение такого положения в любой части линии, при котором нанесенные точки всегда располагаются на линии; в) измерение промежутков между соседними дугами окружностей.

1 Для некоторых картографических проекций (в частности для карт мира и карт океанов) дополнительные указания могут отсутствовать.

Оформление работы. Таблица вычерчивается на белом листе бумаги формата А4 (ориентация листа: альбомная) сначала в карандаше, затем обводится черной гелевой ручкой. Размер таблицы 18*27 см. Отступ с правого края листа 1,2 см, остальные отступы по 1,5 см. Таблица состоит из 8 колонок (ширина слева направо в см: 1, 3, 3, 4, 4, 4, 4, 4) и 7 строк, высота первой – 3 см, остальные по 2.5 см. Сверху посередине подписывается название работы «Определение картографических проекций». В правом нижнем углу под таблицей подписывается ФИО исполнителя, кафедра, курс и год.

Пример выполнения задания.

Определить картографическую проекцию (Карта 1).

На карте изображена территория бывшего СССР, поэтому определение следует проводить по таблице 10. Форма рамки – прямоугольная. Меридианы изображены прямыми, что легко проверить, приложив к линии любого меридиана линейку. Параллели изображены дугами концентрических окружностей: любые три точки линии любой параллели, перенесенные на кальку, всегда можно совместить, поворачивая кальку, с разными частями этой линии; промежутки же между двумя соседними параллелями остаются постоянными. Таким образом, по виду картографической сетки проекция является нормальной конической. Расстояния между параллелями по среднему меридиану остаются постоянными. Следовательно, проекция равнопромежуточная по меридианам.

Используя дополнительные признаки проекции – величину отстояния точки пересечения меридианов от параллели в 90°, – уточняем по определителю (табл. 7) название – нормальная коническая равнопромежуточная проекция Каврайского. Результаты определения проекции представлены в таблице 2.

Сроки выполнения. Работа рассчитана на одно практическое занятие.