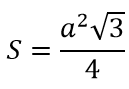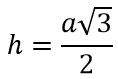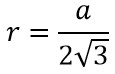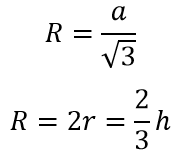В данной статье мы рассмотрим определение и свойства равностороннего (правильного) треугольника. Также разберем пример решения задачи для закрепления теоретического материала.
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Определение равностороннего треугольника
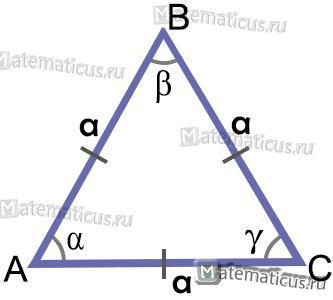
Равносторонним (или правильным) называется треугольник, в котором все стороны имеют одинаковую длину. Т.е. AB = BC = AC.
Примечание: правильный многоугольник – это выпуклый многоугольник, имеющий равные стороны и углы между ними.
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Свойства равностороннего треугольника
Свойство 1
В равностороннем треугольнике все углы равны 60°. Т.е. α = β = γ = 60°.
Свойство 2
В равностороннем треугольнике высота, проведенная к любой из сторон, одновременно является биссектрисой угла, из которого она проведена, а также медианой и серединным перпендикуляром.
CD – медиана, высота и серединный перпендикуляр к стороне AB, а также биссектриса угла ACB.
Свойство 3
В равностороннем треугольнике биссектрисы, медианы, высоты и серединные перпендикуляры, проведенные ко всем сторонам, пересекаются в одной точке.
Свойство 4
Центры вписанной и описанной вокруг равностороннего треугольника окружностей совпадают и находятся на пересечении медиан, высот, биссектрис и серединных перпендикуляров.
Свойство 5
Радиус описанной вокруг равностороннего треугольника окружности в 2 раза больше радиуса вписанной окружности.
- R – радиус описанной окружности;
- r – радиус вписанной окружности;
- R = 2r.
Свойство 6
В равностороннем треугольнике, зная длину стороны (условно примем ее за “a”), можно вычислить:
1. Высоту/медиану/биссектрису:
2. Радиус вписанной окружности:
3. Радиус описанной окружности:
4. Периметр:
5. Площадь:
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Пример задачи
Дан равносторонний треугольник, сторона которого равна 7 см. Найдите радиус описанной вокруг и вписанной окружности, а также, высоту фигуры.
Решение
Применим формулы, приведеные выше, для нахождения неизвестных величин:
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Правильный треугольник. Площадь правильного треугольника
Правильный треугольник — треугольник, у которого все стороны равны. Каждый угол правильного треугольника равен градусов.
Правильный треугольник называют еще равносторонним.
Каждая из высот правильного треугольника является также его медианой и биссектрисой.
Центры вписанной и описанной окружностей правильного треугольника совпадают.
Пусть сторона правильного треугольника равна .
Высота правильного треугольника:
Радиус окружности, вписанной в правильный треугольник: .
Радиус описанной окружности в два раза больше: .
Площадь правильного треугольника: .
Все эти формулы легко доказать. Если вы нацелены на решение задач части — докажите их самостоятельно.
. Сторона правильного треугольника равна . Найдите радиус окружности, вписанной в этот треугольник.
Задача решается в одну строчку. Радиус вписанной окружности .
. Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна .
Сравним формулы для высоты правильного треугольника и радиуса вписанной окружности. Очевидно, радиус вписанной окружности равен высоты.
. Сторона правильного треугольника равна . Найдите радиус окружности, описанной около этого треугольника.
Радиус окружности, описанной вокруг правильного треугольника, равен .
Видео:Радиус описанной окружностиСкачать

Равносторонний (правильный) треугольник
Равносторонний или правильный треугольник — треугольник, у которого три стороны равны. Все углы равностороннего треугольника равны.
Равносторонним треугольником называется такой треугольник, у которого все стороны равны, то есть АВ = ВС = АС (рис. 1)
Свойства равностороннего (правильного) треугольника
- Все углы равностороннего треугольника равны по 60°
∠А=∠С=∠В=60°
- Биссектрисы треугольника являются медианами и высотами, то есть равны и точка их пересечения, является центром вписанной окружности (рис. 2).
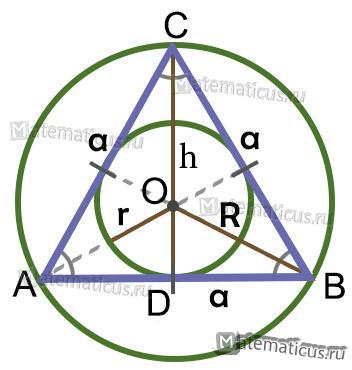
Из (рис. 2) обозначения:
h — высота=биссектриса=медиана
R — радиус описанной окружности
r — радиус вписанной окружности
a — стороны правильного треугольника
Формула периметра равностороннего треугольника:
P=3·a
Формула площади правильного треугольника:
Формула высоты (или медианы или биссектрисы) равностороннего треугольника:
Радиус вписанной окружности в равносторонний треугольник:
Радиус описанной окружности в равносторонний треугольник:
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.6 / 5. Количество оценок: 5
🎥 Видео
9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Формулы радиусов описанной и вписанной окружностей правильного многоугольника 2Скачать

Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

ЕГЭ профиль #3 / Радиус описанной окружности / Равносторонний треугольник / решу егэСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Задача 6 №27909 ЕГЭ по математике. Урок 129Скачать

Геометрия. 9 класс. Формулы для нахождения радиусов вписанной и описанной окружностей треугольникаСкачать

№706. Найдите сторону равностороннего треугольника, если радиус описанной около него окружностиСкачать

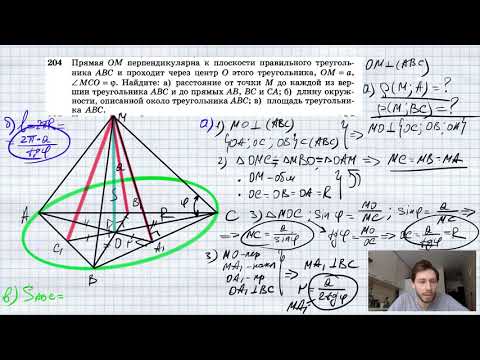
№204. Прямая ОМ перпендикулярна к плоскости правильного треугольника ABC и проходит через центр ОСкачать
Построить описанную окружность (Задача 1)Скачать

Вписанная и описанная около равнобедренного треугольника, окружностьСкачать

найти радиус окружности, описанной вокруг треугольникаСкачать

Геометрия 9 класс (Урок№21 - Правильный многоугольник. Описанная и вписанная окружность.)Скачать

Формулы для радиусов вписанной и описанной окружностей треугольника Геометрия 9классСкачать