Как нарисовать треугольник в проекции (3 видео)

Проекции треугольника, многоугольника и круга

Для примера изобразим прямоугольник ABCD без осей проекций (рис. 115, а). Расстояние горизонтальной и профильной проекций от фронтальной проекции выберем произвольно. Встает вопрос о том, можно ли теперь «восстановить» положение осей, а следовательно, и плоскостей проекций. Для построения постоянной прямой чертежа (рис. 115, б) используем горизонтальную и профильную проекции любой точки, например точки А. Через точку А₁ проведем горизонтальную линию связи, а через точку А₃ — вертикальную линию связи. Проведенные прямые пересекутся между собой в точке А₀, через которую проведем постоянную прямую k₁₂₃ под углом 45 градусов к горизонтальной линии связи. Очевидно, что постоянная прямая будет единственной. Этого нельзя сказать о системе координатных плоскостей, которых может быть много. Действительно, одну из систем можно определить, приняв горизонтально-вертикальную линию связи за направление осей проекций x₁₂ и z₂₃. Точка A₀ будет для этой системы началом координат O₁₂₃. Плоскость прямоугольника будет прикасаться своей стороной AD к фронтальной плоскости проекции П₂. Вторую систему можно получить, если провести координатные оси х’₁₃ и z’₂₃ через точку О’₁₂₃, являющуюся точкой пересечения постоянной прямой с линией D₂D₃. В новой системе прямоугольник будет стоять на горизонтальной плоскости проекций П1, пересекаясь с ней по прямой DC. В промежутке между осями первых двух систем можно провести еще большое количество осей, которые определят новые системы плоскостей. Одну из таких систем определяют оси х₂1₂ и z₂2₃, пересекающиеся между собой в точке О₁, являющейся началом координат третьей системы плоскостей. В последнем случае прямоугольник отстоит от всех трех плоскостей проекций.

Итак, найдя постоянную прямую чертежа, мы можем построить одну из возможных систем плоскостей проекций. Очевидно, что начало координат любой системы должно находиться на постоянной прямой чертежа. Отсюда следует, что постоянная прямая чертежа является геометрическим местом точек, фиксирующих начало координат всех возможных систем плоскостей проекций П₂, П₃.

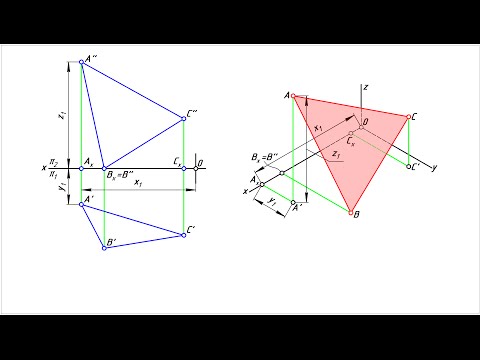
При построении проекций четырехугольника общего положения нельзя взять четыре произвольные точки. Как только мы возьмем три точки, плоскость определится, и четвертую точку надо строить при условии, чтобы она принадлежала этой плоскости. Практически пользуются диагоналями проекций четырехугольника (рис. 115, в).

Фронтальную проекцию четырехугольника ABCD Рис. 116 строим произвольно; также произвольно строим горизонтальные проекции трех точек А₁, В₁ и С₁ треугольника A₁B₁C₁. Для построения горизонтальной проекции D₁ точки D проводим фронтальные проекции А₂С₂ и D₂B₂ диагоналей четырехугольника.

Проекции диагоналей пересекутся между собой в точке Е₂. Находим горизонтальную проекцию E₂ этой точки на горизонтальной проекции А₁С₁ будущей диагонали АС; соединяем точки В₁ и E₁ и на продолжении этой линии находим точку D₁ на вертикальной линии связи D₂D₁. При таком построении четырехугольник ABCD будет плоским. Пользуясь вспомогательными прямыми, пересекающимися со сторонами четырехугольника, можно построить проекции пятиугольника, шестиугольника и т. д.

Построим проекции правильного шестиугольника, вписанного в окружность, при горизонтальном их расположении (рис, 116, а). Построение начинаем с проведения окружности; затем вписываем в нее правильный шестиугольник А₁В₁C₁D₁E₁F₁.

Фронтальная проекция шестиугольника изобразится прямой горизонтально расположенной линией A₂D₂, точки B₂F₂ и С₂Е₂, принадлежащие этой линии, попарно совпадут.

В практике нередко приходится строить наклонно расположенные многоугольники, и особенно, окружности. Придадим плоскостям шестиугольника и круга наклонное положение, т. е. расположим их во фронтально-проецирующей плоскости т (рис. 116, б). При таком расположении плоскости прямые FB и ЕС шестиугольника и диаметр HG круга останутся фронтально-проецирующими прямыми и спроецируются на плоскость П₁ в истинную величину. Наоборот, прямые ВС, AD и FE спроецируются с искажением, зависящим от величины угла наклона плоскости т. В связи с этим горизонтальная проекция шестиугольника не будет являться правильным шестиугольником, а горизонтальная проекция круга будет проецироваться эллипсом, большая ось которого H₁G₁, малая — A₁D₁

Аналитический портал Ua-News Главные новости Украины: политика, интернет, шоу-BIZ, спорт, столица.

Содержание

Черчение
Способы построения изометрической проекции плоских фигур, геометрических тел и деталей
Как нарисовать треугольник в проекции
🔍 Видео

Видео:Построение треугольника в трёх проекцияхСкачать

Черчение

Видео:2 2 2 изометрия треугольника и шестиугольникаСкачать

Способы построения изометрической проекции плоских фигур, геометрических тел и деталей

Для выполнения изометрической проекции любой детали необходимо знать правила построения изометрических проекций плоских и объемных геометрических фигур.

Правила построения изометрических проекций геометрических фигур. Построение любой плоской фигуры следует начинать с проведения осей изометрических проекций.

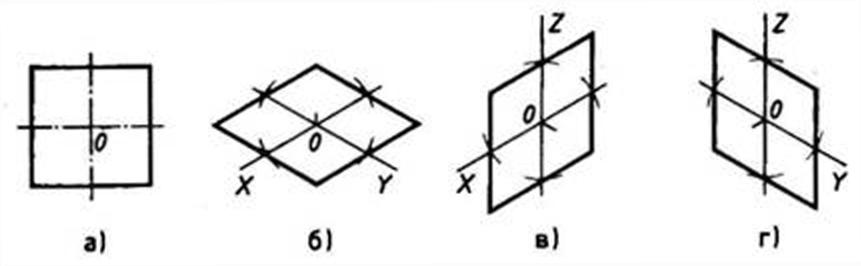
При построении изометрической проекции квадрата (рис. 109) из точки О по аксонометрическим осям откладывают в обе стороны половину длины стороны квадрата. Через полученные засечки проводят прямые, параллельные осям.

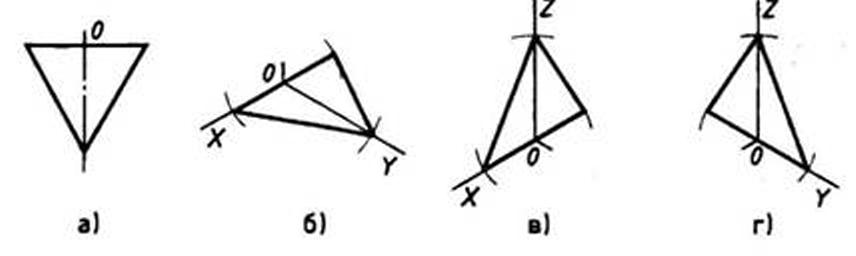
При построении изометрической проекции треугольника (рис. 110) по оси X от точки 0 в обе стороны откладывают отрезки, равные половине стороны треугольника. По оси У от точки О откладывают высоту треугольника. Соединяют полученные засечки отрезками прямых.

Рис. 109. Прямоугольная и изометрические проекции квадрата

Рис. 110. Прямоугольная и изометрические проекции треугольника

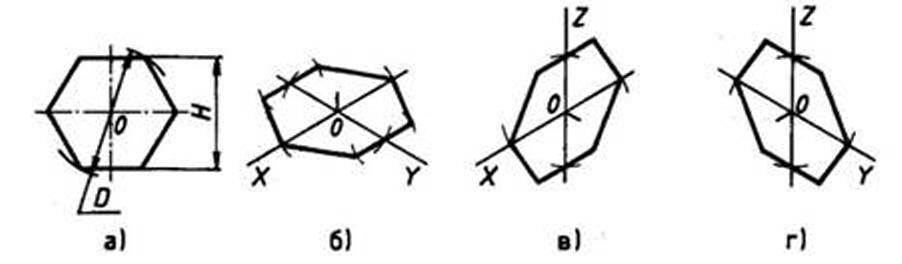
При построении изометрической проекции шестиугольника (рис. 111) из точки О по одной из осей откладывают (в обе стороны) радиус описанной окружности, а по другой — H/2. Через полученные засечки проводят прямые, параллельные одной из осей, и на них откладывают длину стороны шестиугольника. Соединяют полученные засечки отрезками прямых.

Рис. 111. Прямоугольная и изометрические проекции шестиугольника

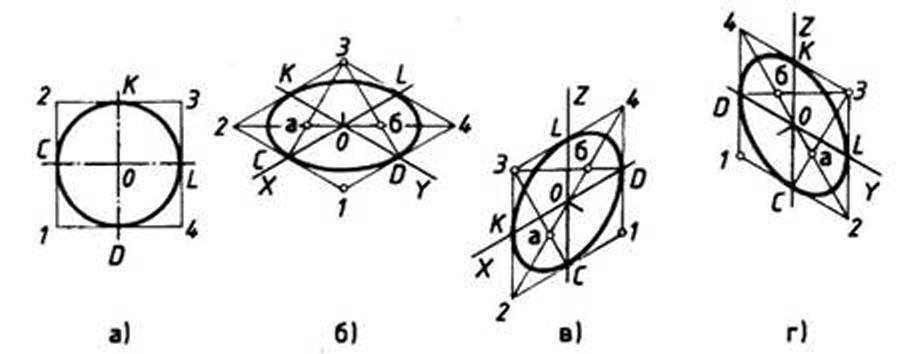
Рис. 112. Прямоугольная и изометрические проекции круга

При построении изометрической проекции круга (рис. 112) из точки О по осям координат откладывают отрезки, равные его радиусу. Через полученные засечки проводят прямые, параллельные осям, получая аксонометрическую проекцию квадрата. Из вершин 1, 3 проводят дуги CD и KL радиусом 3С. Соединяют точки 2 с 4, 3 с С и 3 с D. В пересечениях прямых получаются центры а и б малых дуг, проведя которые получают овал, заменяющий аксонометрическую проекцию круга.

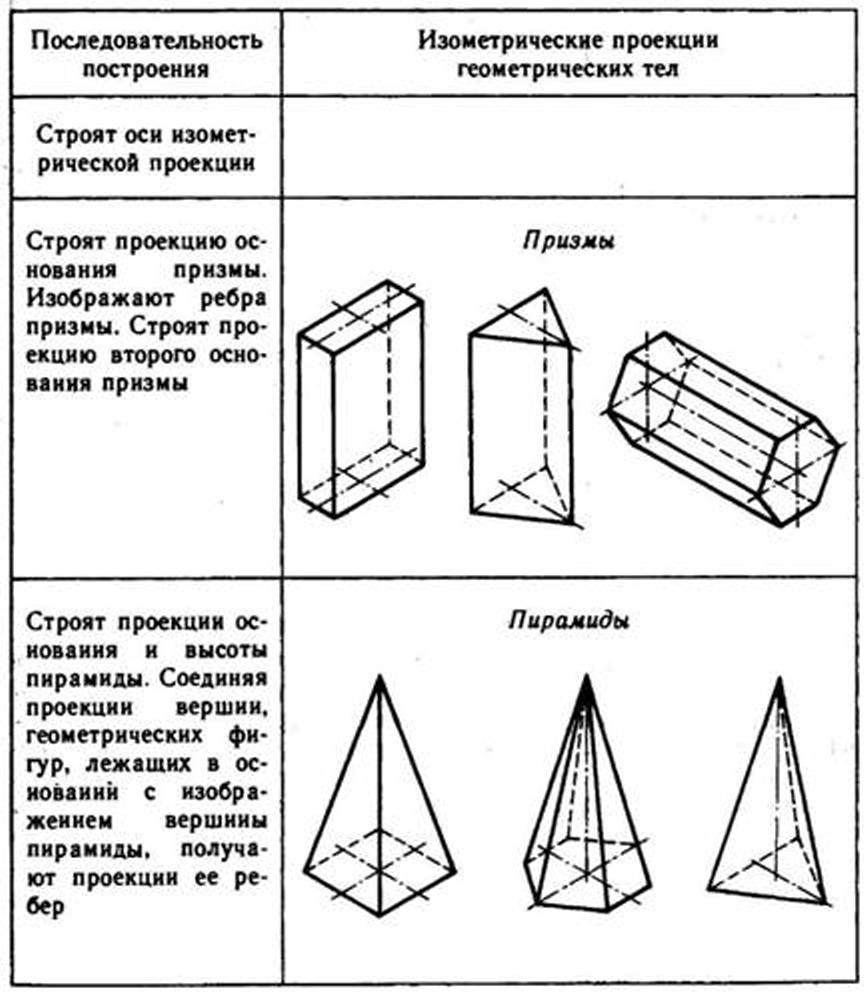
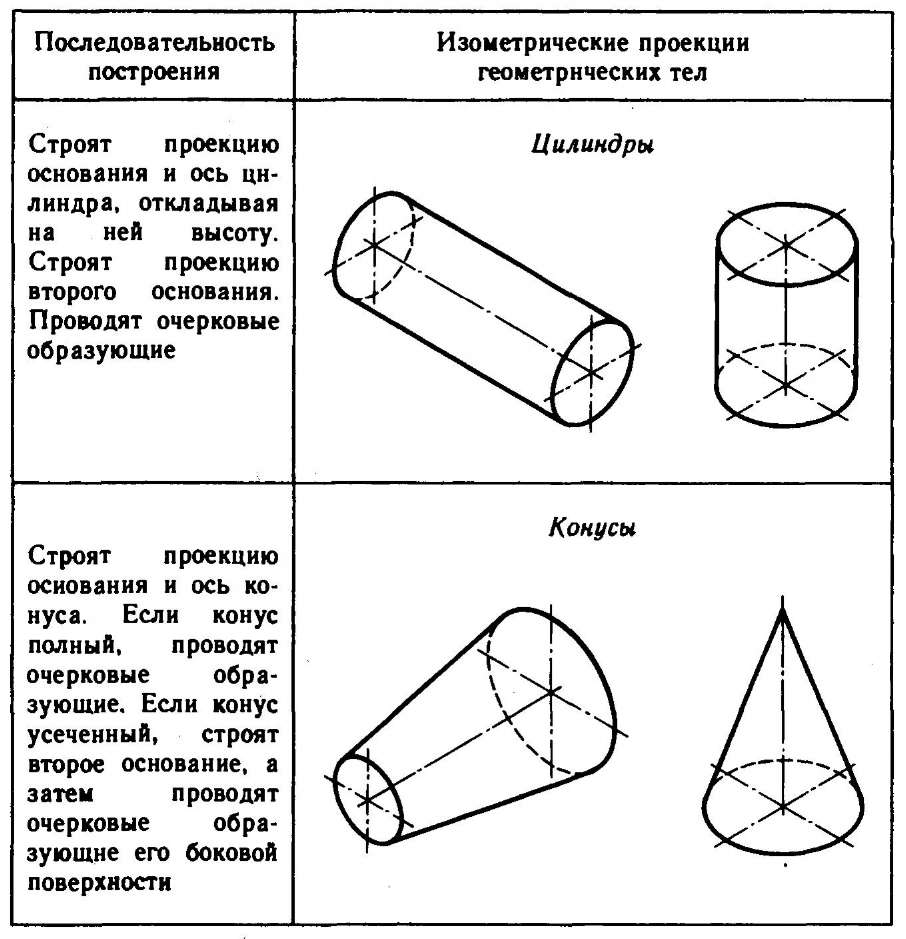
Используя описанные построения, можно выполнить аксонометрические проекции простых геометрических тел (табл. 10).

10. Изометрические проекции простых геометрических тел

Способы построения изометрической проекции детали:

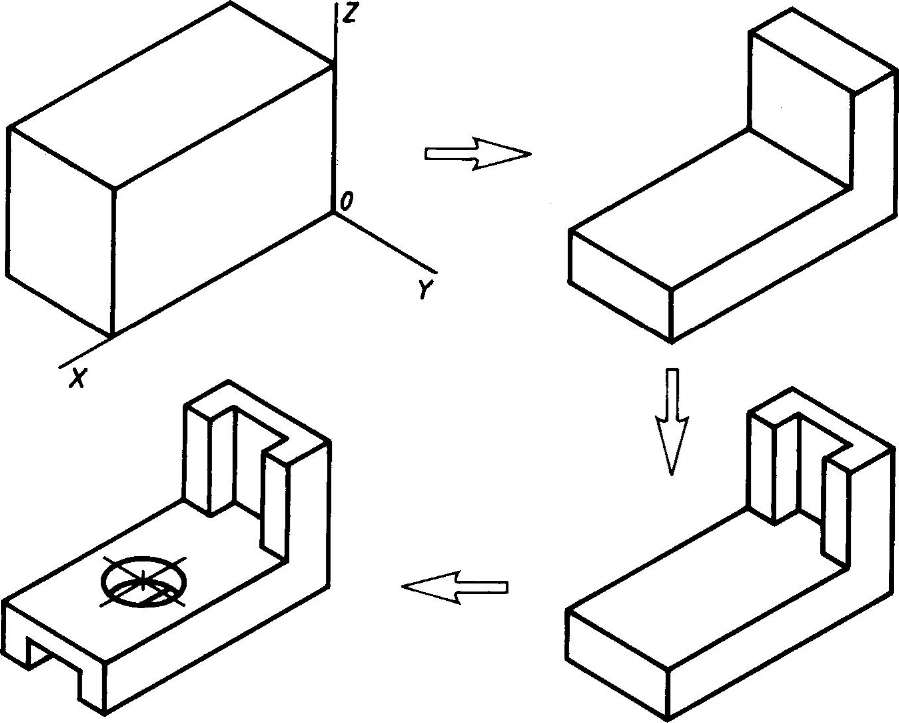
1. Способ построения изометрической проекции детали от формообразующей грани используется для деталей, форма которых имеет плоскую грань, называемую формообразующей; ширина (толщина) детали на всем протяжении одинакова, на боковых поверхностях отсутствуют пазы, отверстия и другие элементы. Последовательность построения изометрической проекции заключается в следующем:

1) построение осей изометрической проекции;

2) построение изометрической проекции формообразующей грани;

3) построение проекций остальных граней посредством изображения ребер модели;

Рис. 113. Построение изометрической проекции детали, начиная от формообразующей грани

4) обводка изометрической проекции (рис. 113).

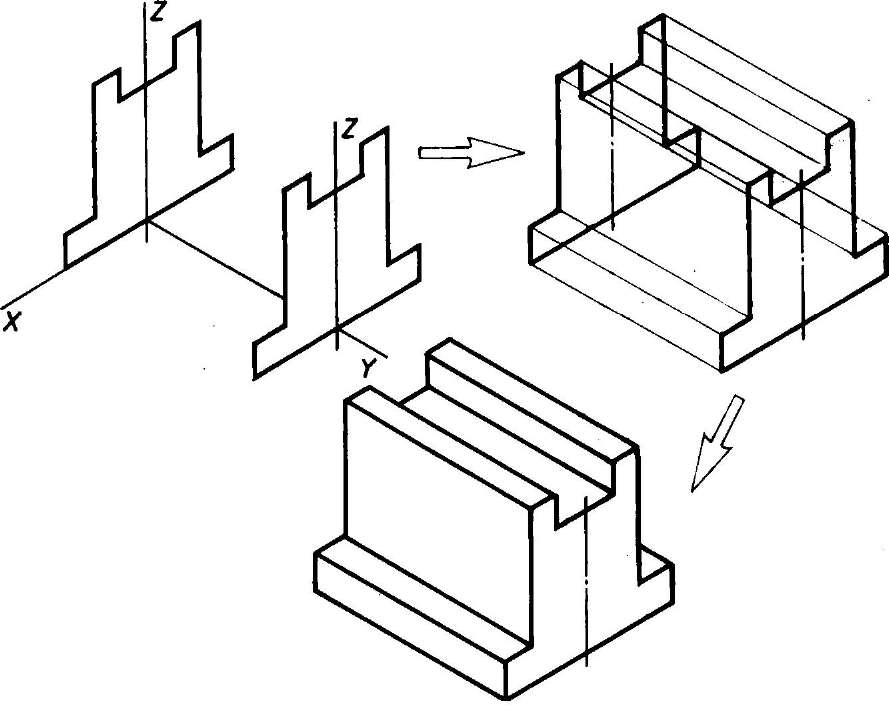
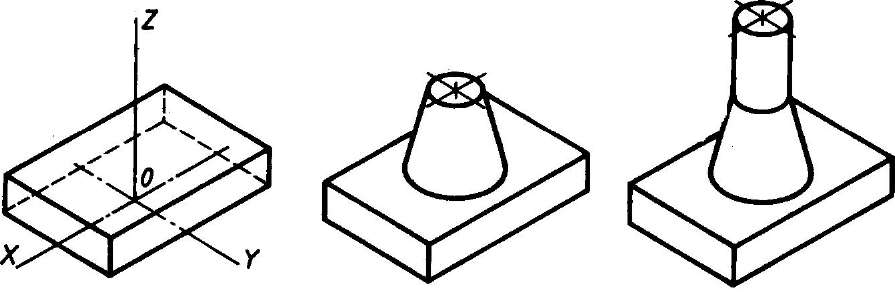
Способ построения изометрической проекции на основе последовательного удаления объемов используется в тех случаях, когда отображаемая форма получена в результате удаления из исходной формы каких-либо объемов (рис. 114).
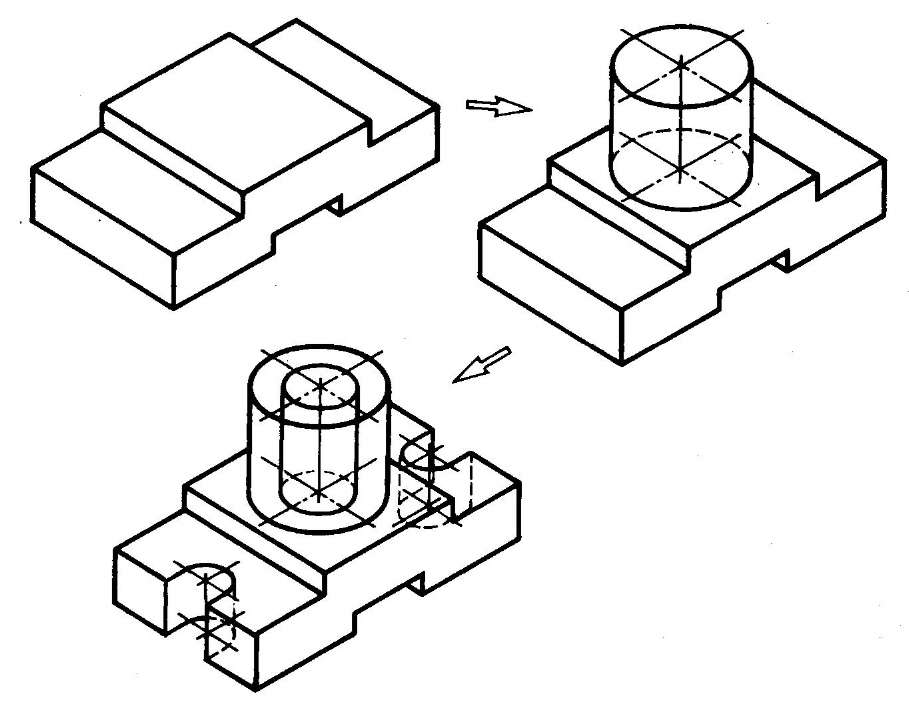
Способ построения изометрической проекции на основе последовательного приращения (добавления) объемов применяется для выполнения изометрического изображения детали, форма которой получена из нескольких объемов, соединенных определенным образом друг с другом (рис. 115).
Комбинированный способ построения изометрической проекции. Изометрическую проекцию детали, форма которой получена в результате сочетания различных способов формообразования, выполняют, используя комбинированный способ построения (рис. 116).

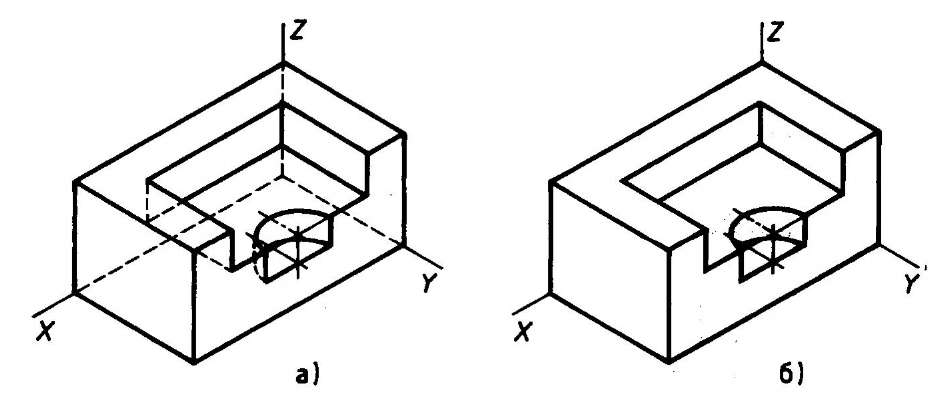
Аксонометрическую проекцию детали можно выполнять с изображением (рис. 117, а) и без изображения (рис. 117, б) невидимых частей формы.

Рис. 114. Построение изометрической проекции детали на основе последовательного удаления объемов

Рис. 115 Построение изометрической проекции детали на основе последовательного приращения объемов

Рис. 116. Использование комбинированного способа построения изометрической проекции детали

Рис. 117. Варианты изображения изометрических проекций детали: а — с изображением невидимых частей;
б — без изображения невидимых частей

Видео:Изометрическая проекция треугольникаСкачать

Как нарисовать треугольник в проекции

Раздел 2: Проецирование (6 часов)

Урок № 9: Рациональные построения в изометрии. Проекции плоских фигур и окружности

Ботвинников А.Д. § 7.2-7.3, 8 [1]

Степакова В. В. § 23 [3]
Вышнепольский И.С. § 13-14 [8]

В ряде случаев построение аксонометрических проекций удобнее начинать с построения фигуры основания. Поэтому рассмотрим, как изображают в аксонометрии плоские геометрические фигуры, расположенные горизонтально.

1. Построение аксонометрической проекции квадрата показано на рис. 1, а и б.

Вдоль оси х откладывают сторону квадрата а, вдоль оси у — половину стороны а/2 для фронтальной диметрической проекции и сторону а для изометрической проекции. Концы отрезков соединяют прямыми.

Рис. 1. Аксонометрические проекции квадрата:

а — фронтальная диметрическая; б — изометрическая

2. Построение аксонометрической проекции треугольника показано на рис. 2, а и б.

Симметрично точке О (началу осей координат) по оси х откладывают половину стороны треугольника а/2, а по оси у — его высоту h (для фронтальной диметрической проекции половину высоты h/2). Полученные точки соединяют отрезками прямых.

Рис. 2. Аксонометрические проекции треугольника:

а — фронтальная диметрическая; б — изометрическая

3. Построение аксонометрической проекции правильного шестиугольника показано на рис. 3.

По оси х вправо и влево от точки О откладывают отрезки, равные стороне шестиугольника. По оси у симметрично точке О откладывают отрезки s/2, равные половине расстояния между противоположными сторонами шестиугольника (для фронтальной диметрической проекции эти отрезки уменьшают вдвое). От точек m и n, полученных на оси у, проводят вправо и влево параллельно оси х отрезки, равные половине стороны шестиугольника. Полученные точки соединяют отрезками прямых.

Рис. 3. Аксонометрические проекции правильного шестиугольника:

а — фронтальная диметрическая; б — изометрическая

4. Построение аксонометрической проекции окружности .

Фронтальная диметрическая проекция удобна для изображения предметов с криволинейными очертаниями, подобных представленными на рис. 4.

Рис.4. Фронтальные диметрические проекции деталей

На рис. 5. дана фронтальная диметрическая проекция куба с вписанными в его грани окружностями. Окружности, расположенные на плоскостях, перпендикулярных к осям х и z, изображаются эллипсами. Передняя грань куба, перпендикулярная к оси у, проецируется без искажения, и окружность, расположенная на ней, изображается без искажения, т. е. описывается циркулем.

Рис.5. Фронтальные диметрические проекции окружностей, вписанных в грани куба

Построение фронтальной диметрической проекции плоской детали с цилиндрическим отверстием .

Фронтальную диметрическую проекцию плоской детали с цилиндрическим отверстием выполняют следующим образом.

1. Строят очертания передней грани детали, пользуясь циркулем (рис. 6, а).

2. Через центры окружности и дуг параллельно оси у проводят прямые, на которых откладывают половину толщины детали. Получают центры окружности и дуг, расположенных на задней поверхности детали (рис. 6, б). Из этих центров проводят окружность и дуги, радиусы которых должны быть равны радиусам окружности и дуг передней грани.

3. Проводят касательные к дугам. Удаляют лишние линии и обводят видимый контур (рис. 6, в).

Рис. 6. Построение фронтальной диметрической проекции детали с цилиндрическими элементами

Изометрические проекции окружностей .

Квадрат в изометрической проекции проецируется в ромб. Окружности, вписанные в квадраты, например, расположенные на гранях куба (рис. 7), в изометрической проекции изображаются эллипсами. На практике эллипсы заменяют овалами, которые вычерчивают четырьмя дугами окружностей.

Рис. 7. Изометрические проекции окружностей, вписанных в грани куба

Построение овала, вписанного в ромб.

1. Строят ромб со стороной, равной диаметру изображаемой окружности (рис. 8, а). Для этого через точку О проводят изометрические оси х и у, и на них от точки О откладывают отрезки, равные радиусу изображаемой окружности. Через точки a, b , с и d проводят прямые, параллельные осям; получают ромб. Большая ось овала располагается на большой диагонали ромба.

2. Вписывают в ромб овал. Для этого из вершин тупых углов (точек А и В) описывают дуги радиусом R, равным расстоянию от вершины тупого угла (точек А и В) до точек a, b или с, d соответственно. От точки В к точкам а и b проводят прямые (рис. 8, б); пересечение этих прямых с большей диагональю ромба дает точки С и D, которые будут центрами малых дуг; радиус R₁ малых дуг равен Са ( Db). Дугами этого радиуса сопрягают большие дуги овала.

Рис. 8. Построение овала в плоскости, перпендикулярной оси z.

Так строят овал, лежащий в плоскости, перпендикулярной к оси z (овал 1 на рис. 7). Овалы, находящиеся в плоскостях, перпендикулярных к осям х (овал 3) и у (овал 2), строят так же, как овал 1., только построение овала 3 ведут на осях у и z (рис. 9, а), а овала 2 (см. рис. 7) — на осях х и z (рис. 9, б).

Рис. 9. Построение овала в плоскостях, перпендикулярных осям х и у

Построение изометрической проекции детали с цилиндрическим отверстием .

Если на изометрической проекции детали нужно изобразить сквозное цилиндрическое отверстие, просверленное перпендикулярно передней грани, представленное на рисунке. 10, а.

Построения выполняет следующим образом.

1. Находят положение центра отверстия на передней грани детали. Через найденный центр проводят изометрические оси. (Для определения их направления удобно воспользоваться изображением куба на рис. 7.) На осях от центра откладывают отрезки, равные радиусу изображаемой окружности (рис. 10, а).

2. Строят ромб, сторона которого равна диаметру изображаемой окружности; проводят большую диагональ ромба (рис. 10, б).

3. Описывают большие дуги овала; находят центры для малых дуг (рис. 10, в).

4. Проводят малые дуги (рис. 10, г).

5. Строят такой же овал на задней грани детали и проводят касательные к обоим овалам (рис. 10, д).