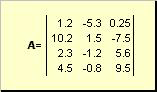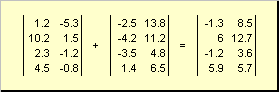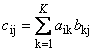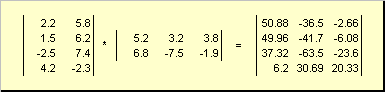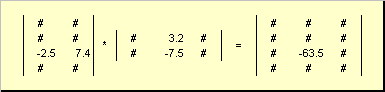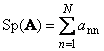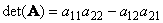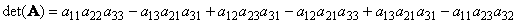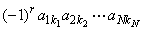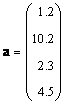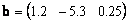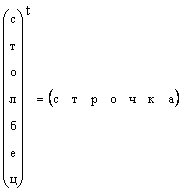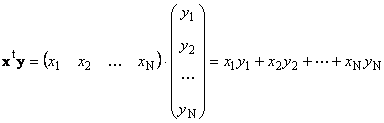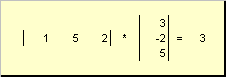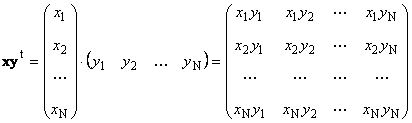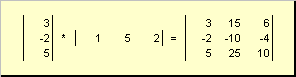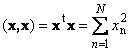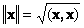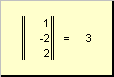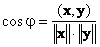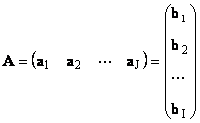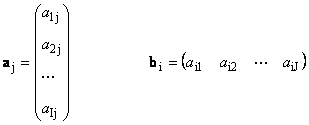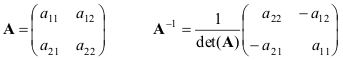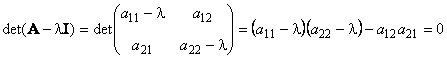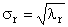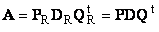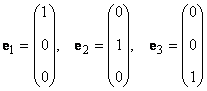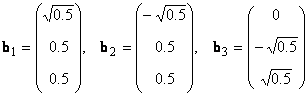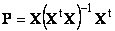4 -е занятие по MATLAB
ЛАБОРАТОРНАЯ РАБОТА №4
I. Базовые операции символьной математики
системы MATLAB — SIMBOLIC MATHEMATICS TOOLBOX
1. Создание символьных переменных и массивов (x, y, z, a, b, c и т.д.).
Первый способ c помощью команды sym: x = sym(‘x’); y = sym(‘y’); z = sym(‘z’);
Второй способ с помощью команды syms: syms a b c;
1.1. Создание символьных матриц А1 (А2) или массивов:
1-й способ : A1 = sym(‘[a1 b1 c1;d1 e1 f1;g1 h1 k1]’); % матрица А1 размера 3 ´ 3
% Вывод матрицы А1 в командной строке
» A1 % После набора А1 нажать клавишу Enter
2- й способ : syms a b c d e f g h k
A2 = [a2 b2 c2;d2 e2 f2;g2 h2 k2]; % Матрица А2 размера 3 ´ 3
% Вывод матрицы А2 в командной строке
1.2. Проверить рабочую область c помощью команды whos.
1.3. Символьные числовые матрицы и элементы:
Ac1=sym([1 3 7;2 4 6;1 7 5]); % Без апострофа
Ас2 = sym(‘7’); % С апострофом
1.4. Детерминант символьной матрицы — det :
» det(A1) % Без присвоения результата
» D 2= det ( A 2) % С присвоением результата ячейке под именем D 2
» det ( Ac 1) % Детерминант символьной числовой матрицы
% Детерминант матрицы 2-го порядка A 3= sym (‘[ a 1 b 1; c 1 d 1]’)
1 .5. Выделение диагонали заданной символьной матрицы:
1.6. Выделение диагонали символьной числовой матрицы
1.7. Создание символьной диагональной матрицы по заданной:
1.8. Создание числовой символьной диагональной матрицы по заданной
1.9. Вычисление собственных значений и собственных векторов символьно-числовой матрицы.
Собственные векторы — это такие векторы v , которые преобразуются матрицей А в векторы, отличающиеся от исходных лишь скалярным множителем s :

» A=sym([-1 0 0;2 -2 0;0 4 -2.5])
% Вычисление собственных векторов и собственных значений квадратной матрицы А — eig
v = % Матрица правых собственных векторов матрицы А
s = % Диагональная матрица собственных значений матрицы А
% Справедливо следующее спектральное разложение: 
% Спектральное разложение может быть осуществлено по вектору столбцу, например
» A*v(:,2) % По второму столбцу
» v(:,2)*s(2,2) % По второму столбцу
% Первый собственный вектор v1 — это первый столбец матрицы v: v1=(0, 1, 8)
% Второй собственный вектор v2 — это второй столбец матрицы v: v2=(1, 2 ,16/3)
% Третий собственный вектор v3 — это третий столбец матрицы v: v3=(0, 0 ,1)
% Собственные числа матрицы А: s1=-2, s2=-1, s3=-5/2=-2.5
% Справедливы следующие соотношения:
Задание: Найти собственные векторы и собственные значения матрицы [7,-2,0;-2,6,-2;0,-2,5] , проверить результат.
2. Графические построения символьных функций — ezplot .
2.1. 1-й способ. Область определения по умолчанию от -2* pi до 2* pi
» syms t % Определение символьной переменной
2.2. 2-й способ обращения к функции ezplot . Задаваемая область определения
2 .3. 3-й способ обращения к функции ezplot . Определение функции под знаком ezplot
2 .4. 4-й способ обращения к функции ezplot .
» ezplot exp(-0.5*t)*cos(5*t) [0 9],grid
» ezplot sin(t)/t [ -12 12 ],grid
3. Свойства собственнх значений матрицы:
где 




% В системе MATLAB
» trace(A) % След матрицы А
» sum(eig(A)) % Сумма собственных значений матрицы А
» det(A) % Определитель матрицы А
» prod(eig(A)) % Произведение собственных значений матрицы А
4. Создание полиномов и характеристических полиномов.
4.1. Создание полинома по вектору заданных коэффициентов — poly2sym .
» poly2sym(c) % Вектор коэффициентов может быть непосредственно введен в poly2sym
% Переменная х устанавливается по умолчанию. Другие переменные следует определять
» c=[2 3 5 7 8]; % Можно определить и как вектор столбец
4.2. Характеристический полином заданной символьно-числовой матрицы
Характеристический полином определяется из следующего характеристического уравнения для заданной матрицы А:



Каждое собственное число матрицы А удовлетворяет ее характеристическому уравнению
» syms s % Задали символьную переменную s
% Для чисто числовой матрицы функция poly определяет только строку коэффициентов
Задание. Вычислить собственные значения матрицы А с присвоением результата и подставить каждое из собственных значений в полученный характеристический полином. Результат должен быть равен нулю. Использовать функцию упрощения результата вычислений simplify.
4.3. Выделение коэффициентов из заданного полинома — sym2poly.
» p=poly2sym([1 3 4 6],s) % Формирование полинома с заданными коэффициентами
» sym2poly(p) % Выделение вектор-строки коэффициентов из заданного полинома
% Полученную вектор-строку можно переопределить с присвоением
Задание. Сформировать характеристический полином по полученному вектору-строки с использованием функции poly2sym по переменной z.
5. Решение символьных конечных уравнений — solve .
5.1. Решение квадратного уравнения
—
» syms x % Задание символьной переменной х
» solve(‘x^2+2*x-8=0’) % Формат записи решателя solve
—
[ -1-i*7^(1/2)] % Комплексное решение, i — мнимая единица
5.2. Решение нелинейных уравнений.
5.3. Решение систем нелинейных уравнений.
—
» simplify([X2,X1]) % Для упрощения результата
5.4. Решение систем трансцендентных уравнений.
Пример. Решить следующую систему трансцендентных уравнений:
где t1, t2, t3 — искомые переменные.
% Функция vpa используется д ля задания количества значащих цифр
O4=(1-0.5)*exp(T3(4))-2*exp(T2(4))+2*exp(T1(4))-1 % Для проверки
% Каждое из 6 решений должно удовлетворять любому из 3-х уравнений
II. Вычисление символьных выражений
с различным представлением результатов.
Вычисление пределов в MATLAB. Вычисление сумм, произведений.
в пакете SIMBOLIC MATHEMATICS TOOLBOX.
1. Представление результата в виде рационального числа — ‘r’ .
1.1. Вычисление дроби 1/3:
» r1=sym(1/3,’r’) % С присвоением результата
1.2. Вычисление натурального логарифма от 3 — 
1.3. Вычисление десятичного логарифма от 3 — 
1.4. Вычисление логарифма по основанию два от 3 — 
Замечание: Представление в виде рационального числа имеет формат либо p/q либо p*2^q, где p, q — целые числа.
2. Представление результата в виде числа с плавающей точкой — ‘f’ .
Все величины представляются в форме ‘1.F’*2^(e) или ‘-1.F’*2^(e), где F — это ряд из 13 шестнадцатиричных цифр, а e — целое число. В случае, когда результат вычисления не может быть представлен точно в форме с плавающей точкой, то выводятся буквы, имеющие то или иное назначение в интерпретации результата.
2.1. Вычисление дроби 1/2:
» f1=sym(1/2,’f’) % Формат записи
% Результат записан в виде точного представления в арифметике с плавающей точкой
2.2. Вычисление дроби 1/5:
% Результат записан в виде приближенного (буква а — approximately) представления в арифметике с плавающей точкой.
3. Рациональное число с оценкой погрешности полученного представления —‘e’.
Рациональное представление добавляется переменной ‘eps’, которая оценивает разницу между теоретическим рациональным выражением (результатом) и его действительной величиной с плавающей точкой.
3.1. Вычислить дробь 1/2:
1/2 % Результат как и в случае рационального представления
3.2. Вычислить дробь 1/3:
3.3. Вычислить выражение 
3.4. Вычислить дробь 3/33
4. Формат десятичного числа — ‘d’ .
4.1. Вычислить дробь 1/3:
.33333333333333331482961625624739 % По умолчанию поддерживаются 16 цифр %мантиссы полученного числа
4.2. вычислить выражение 
4.3. Вычислить дробь 1/3 с 23 знаками в мантиссе с использованием функции vpa :
4.4. Вычислить дробь 1/3 с 23 знаками в мантиссе с использованием vpa и digits
% Использование только digits приводит к выводу результата с заданным количеством цифр, но %с ограниченной точностью (в формате ‘d’):
5. Вычисление пределов — limit.
Вычисление пределов от символьных выражений производится с помощью встроенной функции limit . Соответствие между традиционным математическим описанием и символьным системы MATLAB приводится в таблице 1.
Таблица 1
Традиционное математическое действие
Команда MATLAB


Примечание: символ бесконечность ( 
5.1. Вычислить предел выражения 
1 % Предел отношения равен единицы
5.2. Вычислить предел выражения 
exp(1) % Ответ: число е в первой степени
5.3. Вычислить предел выражения 
-inf % Ответ: минус бесконечность
5.4. Вычислить предел выражения 
inf % Ответ: бесконечность (т.е. плюс бесконечность)
limit((sin(x+h)-sin(x))/h,h,0) returns cos(x)
5.5. Вычислить предел выражения 
» limit(y5,h,0) % Вычисление предела по одной из переменных — по h
6 . Дифференцирование функций одной переменной — diff .
6.1. Найти производную функции 
6.2. Найти производную функции 
» diff(sin(x+h)/x) % Формат записи без предварительного присвоения
6.3. Найти производную функции 
» diff(sin(x+h)/x,h) % В записи указывается имя символьной переменной, по которой
6.4. Найти вторую производную от функции 
6.5. Найти вторую производную от функции 
» diff(sin(x+h)/x,2) % Цифра два указывает на порядок производной
6.6. Найти третью производную от функции 
7. Интегрирование функции одной переменной — int .
7.1. Вычисление неопределенного интеграла:
% Вычислить интеграл 
% Вычислить интеграл 
» int((x+h)^2) % По умолчанию интегрирование ведется по переменной х
% Вычислить неопределенный интеграл от функции 
% Вычислить неопределенный интеграл от функции 
1/2*x^2+2*h*x+h^2*log(x) % В ответе имеется в виду натуральный логарифм
7.2. Вычисление определенного интеграла.
% Вычислить определенный интеграл 
% Вычислить определенный интеграл 
8. Решение обыкновенных дифференциальных уравнений в символьном виде — dsolve .
Решатель дифференциальных уравнений может быть использован, если решение существует в аналитическом виде. Практически это означает, что решателем dsolve можно пользоваться только при поиске решения линейного дифференциального уравнения (или системы линейных уравнений).
8 .1. Решить дифференциальное уравнение 

% Создадим следующий сценарий под именем sdif1 :
% Решение диф.уравнения в символьном виде
% Область построения графика решения можно задавать без квадратных скобок
8 .2. Решить систему однородных дифференциальных уравнений 

% Создадим следующий сценарий под именем sdif2 :
ezplot(x1,0,13),grid,hold on,ezplot(x2,[0,13]),title (‘Однородная система 2-х уравнений’)
8.3. Решить систему неоднородных дифференциальных уравнений



% Создадим следующий сценарий под именем sdif3 :
ezplot(x1,[0,5]),grid,hold on,ezplot(x2,[0,9]),title( ‘ Неоднородная система 2-х уравнений ‘)
8.4. Решить дифференциальное уравнение 2-го порядка 
% Создадим следующий сценарий под именем sdif4 :
ezplot(x,[-0.2 9]),grid,title (‘Д иф.уравнение 2-го порядка ‘)
8.5. Решить дифференциальное уравнение 3-го порядка 
% Создадим следующий сценарий под именем sdif5 :
ezplot(x,[-0.2 21]),grid,title (‘Диф.уравнение 3-го порядка’)
8.6. Решить неоднородную систему дифференциальных уравнений 3-го порядка




% Создадим следующий сценарий под именем sdif6 :
ezplot(x1,[-1,19]),grid, hold on,ezplot(x2,[-1,19],
title (‘Н еоднородная система 3-го порядка ‘),
% Функция ezplot не позволяет строить графики с заданными цветами. Применим fplot . Для этого в функцию fplot следует вставить решения из командного окна MATLAB. Например, решение по первой координате имеет вид
% Тогда формат записи fplot для графика по х1 будет следующий (с красным цветом):
% Через hold on можно добавить еще fplot по второй координате х2 и по третьей х3.
¾ Для объекта с передаточной функцией 
¾ Для того же объекта с передаточной функцией W(s) записать систему дифференциальных уравнений первого порядка, решить ее и сравнить с решением соответствующего дифференциального уравнения 3-го порядка.
¾ Исследовать переходной процесс по выходным координатам двух колебательных звеньев, соединенных последовательно. Передаточные функции звеньев принять в виде:
¾ Решение в символьном виде систем дифференциальных уравнений сравнить с решением численного метода с помощью решателя ode45.
- Собственные векторы в матлаб
- Syntax
- Description
- Examples
- Eigenvalues of Matrix
- Eigenvalues and Eigenvectors of Matrix
- Sorted Eigenvalues and Eigenvectors
- Left Eigenvectors
- Eigenvalues of Nondiagonalizable (Defective) Matrix
- Generalized Eigenvalues
- Generalized Eigenvalues Using QZ Algorithm for Badly Conditioned Matrices
- Generalized Eigenvalues Where One Matrix is Singular
- Input Arguments
- A — Input matrix square matrix
- B — Generalized eigenvalue problem input matrix square matrix
- balanceOption — Balance option ‘balance’ (default) | ‘nobalance’
- algorithm — Generalized eigenvalue algorithm ‘chol’ | ‘qz’
- outputForm — Output format of eigenvalues ‘vector’ | ‘matrix’
- Output Arguments
- e — Eigenvalues (returned as vector) column vector
- V — Right eigenvectors square matrix
- D — Eigenvalues (returned as matrix) diagonal matrix
- W — Left eigenvectors square matrix
- Матрицы и векторы
- 1. Базовые сведения
- 1.1 Матрицы
- 1.2. Простейшие операции с матрицами
- 1.3. Умножение матриц
- 1.4. Квадратные матрицы
- 1.5. След и определитель
- 1.6. Векторы
- 1.7. Простейшие операции с векторами
- 1.8. Произведения векторов
- 1.9. Норма вектора
- 1.10. Угол между векторами
- 1.11. Векторное представление матрицы
- 1.12. Линейно зависимые векторы
- 1.13. Ранг матрицы
- 1.14. Обратная матрица
- 1.15. Псевдообратная матрица
- 1.16. Умножение вектора на матрицу
- 2. Дополнительная информация
- 2.1. Системы линейных уравнений
- 2.2. Билинейные и квадратичные формы
- 2.3. Положительно определенные матрицы
- 2.4. Разложение Холецкого
- 2.5. Полярное разложение
- 2.6. Собственные векторы и собственные значения
- 2.7. Собственные значения
- 2.8. Собственные векторы
- 2.9. Эквивалентные и подобные матрицы
- 2.10. Приведение матрицы к диагональному виду
- 2.11. Разложение по сингулярным значениям (SVD)
- 2.12. Линейное пространство
- 2.13. Базис линейного пространства
- 2.14. Геометрическая интерпретация
- 2.15. Множественность базисов
- 2.16. Подпространство
- 2.17. Проекция на подпространство
- Заключение
Видео:Собственные векторы и собственные значения матрицыСкачать

Собственные векторы в матлаб
Eigenvalues and eigenvectors
Видео:Собственные значения и собственные векторы матрицы (4)Скачать

Syntax
Видео:Собственные векторы и собственные числа линейного оператораСкачать

Description
e = eig( A ) returns a column vector containing the eigenvalues of square matrix A .
[ V , D ] = eig( A ) returns diagonal matrix D of eigenvalues and matrix V whose columns are the corresponding right eigenvectors, so that A*V = V*D .
[ V , D , W ] = eig( A ) also returns full matrix W whose columns are the corresponding left eigenvectors, so that W’*A = D*W’ .
The eigenvalue problem is to determine the solution to the equation A v = λ v, where A is an n -by- n matrix, v is a column vector of length n , and λ is a scalar. The values of λ that satisfy the equation are the eigenvalues. The corresponding values of v that satisfy the equation are the right eigenvectors. The left eigenvectors, w, satisfy the equation w’ A = λ w’.
e = eig( A , B ) returns a column vector containing the generalized eigenvalues of square matrices A and B .
[ V , D ] = eig( A , B ) returns diagonal matrix D of generalized eigenvalues and full matrix V whose columns are the corresponding right eigenvectors, so that A*V = B*V*D .
[ V , D , W ] = eig( A , B ) also returns full matrix W whose columns are the corresponding left eigenvectors, so that W’*A = D*W’*B .
The generalized eigenvalue problem is to determine the solution to the equation A v = λ B v, where A and B are n -by- n matrices, v is a column vector of length n , and λ is a scalar. The values of λ that satisfy the equation are the generalized eigenvalues. The corresponding values of v are the generalized right eigenvectors. The left eigenvectors, w, satisfy the equation w’ A = λ w’ B.
[ ___ ] = eig( A , balanceOption ) , where balanceOption is ‘nobalance’ , disables the preliminary balancing step in the algorithm. The default for balanceOption is ‘balance’ , which enables balancing. The eig function can return any of the output arguments in previous syntaxes.
[ ___ ] = eig( A , B , algorithm ) , where algorithm is ‘chol’ , uses the Cholesky factorization of B to compute the generalized eigenvalues. The default for algorithm depends on the properties of A and B , but is generally ‘qz’ , which uses the QZ algorithm.
If A is Hermitian and B is Hermitian positive definite, then the default for algorithm is ‘chol’ .
[ ___ ] = eig( ___ , outputForm ) returns the eigenvalues in the form specified by outputForm using any of the input or output arguments in previous syntaxes. Specify outputForm as ‘vector’ to return the eigenvalues in a column vector or as ‘matrix’ to return the eigenvalues in a diagonal matrix.
Видео:MatLab. 6.6d. Собственные числа и векторы матриц, функции матрицСкачать

Examples
Eigenvalues of Matrix
Use gallery to create a symmetric positive definite matrix.
Calculate the eigenvalues of A . The result is a column vector.
Alternatively, use outputForm to return the eigenvalues in a diagonal matrix.
Eigenvalues and Eigenvectors of Matrix
Use gallery to create a circulant matrix.
Calculate the eigenvalues and right eigenvectors of A .
Verify that the results satisfy A*V = V*D .
Ideally, the eigenvalue decomposition satisfies the relationship. Since eig performs the decomposition using floating-point computations, then A*V can, at best, approach V*D . In other words, A*V — V*D is close to, but not exactly, 0 .
Sorted Eigenvalues and Eigenvectors
By default eig does not always return the eigenvalues and eigenvectors in sorted order. Use the sort function to put the eigenvalues in ascending order and reorder the corresponding eigenvectors.
Calculate the eigenvalues and eigenvectors of a 5-by-5 magic square matrix.
The eigenvalues of A are on the diagonal of D . However, the eigenvalues are unsorted.
Extract the eigenvalues from the diagonal of D using diag(D) , then sort the resulting vector in ascending order. The second output from sort returns a permutation vector of indices.
Use ind to reorder the diagonal elements of D . Since the eigenvalues in D correspond to the eigenvectors in the columns of V , you must also reorder the columns of V using the same indices.
Both (V,D) and (Vs,Ds) produce the eigenvalue decomposition of A . The results of A*V-V*D and A*Vs-Vs*Ds agree, up to round-off error.
Left Eigenvectors
Create a 3-by-3 matrix.
Calculate the right eigenvectors, V , the eigenvalues, D , and the left eigenvectors, W .
Verify that the results satisfy W’*A = D*W’ .
Ideally, the eigenvalue decomposition satisfies the relationship. Since eig performs the decomposition using floating-point computations, then W’*A can, at best, approach D*W’ . In other words, W’*A — D*W’ is close to, but not exactly, 0 .
Eigenvalues of Nondiagonalizable (Defective) Matrix
Create a 3-by-3 matrix.
Calculate the eigenvalues and right eigenvectors of A .
A has repeated eigenvalues and the eigenvectors are not independent. This means that A is not diagonalizable and is, therefore, defective.
Verify that V and D satisfy the equation, A*V = V*D , even though A is defective.
Ideally, the eigenvalue decomposition satisfies the relationship. Since eig performs the decomposition using floating-point computations, then A*V can, at best, approach V*D . In other words, A*V — V*D is close to, but not exactly, 0 .
Generalized Eigenvalues
Create two matrices, A and B , then solve the generalized eigenvalue problem for the eigenvalues and right eigenvectors of the pair (A,B) .
Verify that the results satisfy A*V = B*V*D .
The residual error A*V — B*V*D is exactly zero.
Generalized Eigenvalues Using QZ Algorithm for Badly Conditioned Matrices
Create a badly conditioned symmetric matrix containing values close to machine precision.
Calculate the generalized eigenvalues and a set of right eigenvectors using the default algorithm. In this case, the default algorithm is ‘chol’ .
Now, calculate the generalized eigenvalues and a set of right eigenvectors using the ‘qz’ algorithm.
Check how well the ‘chol’ result satisfies A*V1 = A*V1*D1 .
Now, check how well the ‘qz’ result satisfies A*V2 = A*V2*D2 .
When both matrices are symmetric, eig uses the ‘chol’ algorithm by default. In this case, the QZ algorithm returns more accurate results.
Generalized Eigenvalues Where One Matrix is Singular
Create a 2-by-2 identity matrix, A , and a singular matrix, B .
If you attempt to calculate the generalized eigenvalues of the matrix B — 1 A with the command [V,D] = eig(BA) , then MATLAB® returns an error because BA produces Inf values.
Instead, calculate the generalized eigenvalues and right eigenvectors by passing both matrices to the eig function.
It is better to pass both matrices separately, and let eig choose the best algorithm to solve the problem. In this case, eig(A,B) returns a set of eigenvectors and at least one real eigenvalue, even though B is not invertible.
Verify A v = λ B v for the first eigenvalue and the first eigenvector.
Ideally, the eigenvalue decomposition satisfies the relationship. Since the decomposition is performed using floating-point computations, then A*eigvec can, at best, approach eigval*B*eigvec , as it does in this case.
Видео:7 4 Собственные векторы и собственные значенияСкачать

Input Arguments
A — Input matrix
square matrix
Input matrix, specified as a real or complex square matrix.
Data Types: double | single
Complex Number Support: Yes
B — Generalized eigenvalue problem input matrix
square matrix
Generalized eigenvalue problem input matrix, specified as a square matrix of real or complex values. B must be the same size as A .
Data Types: double | single
Complex Number Support: Yes
balanceOption — Balance option
‘balance’ (default) | ‘nobalance’
Balance option, specified as: ‘balance’ , which enables a preliminary balancing step, or ‘nobalance’ which disables it. In most cases, the balancing step improves the conditioning of A to produce more accurate results. However, there are cases in which balancing produces incorrect results. Specify ‘nobalance’ when A contains values whose scale differs dramatically. For example, if A contains nonzero integers, as well as very small (near zero) values, then the balancing step might scale the small values to make them as significant as the integers and produce inaccurate results.
‘balance’ is the default behavior. For more information about balancing, see balance .
algorithm — Generalized eigenvalue algorithm
‘chol’ | ‘qz’
Generalized eigenvalue algorithm, specified as ‘chol’ or ‘qz’ , which selects the algorithm to use for calculating the generalized eigenvalues of a pair.
| algorithm | Description |
|---|---|
| ‘chol’ | Computes the generalized eigenvalues of A and B using the Cholesky factorization of B . |
| ‘qz’ | Uses the QZ algorithm, also known as the generalized Schur decomposition. This algorithm ignores the symmetry of A and B . |
In general, the two algorithms return the same result. The QZ algorithm can be more stable for certain problems, such as those involving badly conditioned matrices.
When you omit the algorithm argument, the eig function selects an algorithm based on the properties of A and B . It uses the ‘chol’ algorithm for symmetric (Hermitian) A and symmetric (Hermitian) positive definite B . Otherwise, it uses the ‘qz’ algorithm.
Regardless of the algorithm you specify, the eig function always uses the QZ algorithm when A or B are not symmetric.
outputForm — Output format of eigenvalues
‘vector’ | ‘matrix’
Output format of eigenvalues, specified as ‘vector’ or ‘matrix’ . This option allows you to specify whether the eigenvalues are returned in a column vector or a diagonal matrix. The default behavior varies according to the number of outputs specified:
If you specify one output, such as e = eig(A) , then the eigenvalues are returned as a column vector by default.
If you specify two or three outputs, such as [V,D] = eig(A) , then the eigenvalues are returned as a diagonal matrix, D , by default.
Example: D = eig(A,’matrix’) returns a diagonal matrix of eigenvalues with the one output syntax.
Видео:Собственные векторы и собственные числа линейного оператораСкачать

Output Arguments
e — Eigenvalues (returned as vector)
column vector
Eigenvalues, returned as a column vector containing the eigenvalues (or generalized eigenvalues of a pair) with multiplicity. Each eigenvalue e(k) corresponds with the right eigenvector V(:,k) and the left eigenvector W(:,k) .
When A is real symmetric or complex Hermitian, the values of e that satisfy A v = λ v are real.
When A is real skew-symmetric or complex skew-Hermitian, the values of e that satisfy A v = λ v are imaginary.
V — Right eigenvectors
square matrix
Right eigenvectors, returned as a square matrix whose columns are the right eigenvectors of A or generalized right eigenvectors of the pair, (A,B) . The form and normalization of V depends on the combination of input arguments:
[V,D] = eig(A) returns matrix V , whose columns are the right eigenvectors of A such that A*V = V*D . The eigenvectors in V are normalized so that the 2-norm of each is 1.
If A is real symmetric, Hermitian, or skew-Hermitian, then the right eigenvectors V are orthonormal.
[V,D] = eig(A,’nobalance’) also returns matrix V . However, the 2-norm of each eigenvector is not necessarily 1.
[V,D] = eig(A,B) and [V,D] = eig(A,B,algorithm) return V as a matrix whose columns are the generalized right eigenvectors that satisfy A*V = B*V*D . The 2-norm of each eigenvector is not necessarily 1. In this case, D contains the generalized eigenvalues of the pair, (A,B) , along the main diagonal.
When eig uses the ‘chol’ algorithm with symmetric (Hermitian) A and symmetric (Hermitian) positive definite B , it normalizes the eigenvectors in V so that the B -norm of each is 1.
Different machines and releases of MATLAB ® can produce different eigenvectors that are still numerically accurate:
For real eigenvectors, the sign of the eigenvectors can change.
For complex eigenvectors, the eigenvectors can be multiplied by any complex number of magnitude 1.
For a multiple eigenvalue, its eigenvectors can be recombined through linear combinations. For example, if A x = λ x and A y = λ y , then A( x+ y) = λ( x+ y) , so x+ y also is an eigenvector of A.
D — Eigenvalues (returned as matrix)
diagonal matrix
Eigenvalues, returned as a diagonal matrix with the eigenvalues of A on the main diagonal or the eigenvalues of the pair, (A,B) , with multiplicity, on the main diagonal. Each eigenvalue D(k,k) corresponds with the right eigenvector V(:,k) and the left eigenvector W(:,k) .
When A is real symmetric or complex Hermitian, the values of D that satisfy A v = λ v are real.
When A is real skew-symmetric or complex skew-Hermitian, the values of D that satisfy A v = λ v are imaginary.
W — Left eigenvectors
square matrix
Left eigenvectors, returned as a square matrix whose columns are the left eigenvectors of A or generalized left eigenvectors of the pair, (A,B) . The form and normalization of W depends on the combination of input arguments:
[V,D,W] = eig(A) returns matrix W , whose columns are the left eigenvectors of A such that W’*A = D*W’ . The eigenvectors in W are normalized so that the 2-norm of each is 1. If A is symmetric, then W is the same as V .
[V,D,W] = eig(A,’nobalance’) also returns matrix W . However, the 2-norm of each eigenvector is not necessarily 1.
[V,D,W] = eig(A,B) and [V,D,W] = eig(A,B,algorithm) returns W as a matrix whose columns are the generalized left eigenvectors that satisfy W’*A = D*W’*B . The 2-norm of each eigenvector is not necessarily 1. In this case, D contains the generalized eigenvalues of the pair, (A,B) , along the main diagonal.
If A and B are symmetric, then W is the same as V .
Different machines and releases of MATLAB can produce different eigenvectors that are still numerically accurate:
For real eigenvectors, the sign of the eigenvectors can change.
For complex eigenvectors, the eigenvectors can be multiplied by any complex number of magnitude 1.
For a multiple eigenvalue, its eigenvectors can be recombined through linear combinations. For example, if A x = λ x and A y = λ y , then A( x+ y) = λ( x+ y) , so x+ y also is an eigenvector of A.
Видео:Собственные значения и собственные векторыСкачать

Матрицы и векторы
© 2007 Алексей Померанцев
В этом документе собраны основные сведения из алгебры матриц и векторов, которые используются в хемометрике. Приведенный текст не может служить учебником по матричной алгебре — он скорее является конспектом, справочником в этой области. Более глубокое и систематическое изложение может быть найдено в литературе.
Текст разбит на две части названные — «Базовые сведения» и «Дополнительная информация». В первой части изложены положения, минимально необходимые для понимания хемометрики, а во второй части — факты, которые необходимо знать для более глубокого постижения методов многомерного анализа. Изложение иллюстрируется примерами, выполненными в рабочей книге Excel Matrix.xls, которая сопровождает этот документ.
Ссылки на примеры помещены в текст как объекты Excel. Эти примеры имеют абстрактный характер, они никак не привязаны к задачам аналитической химии. Реальные примеры использования матричной алгебры в хемометрике рассмотрены в других текстах, посвященных разнообразным хемометрическим приложениям.
Большинство измерений, проводимых в аналитической химии, являются не прямыми, а косвенными . Это означает, что в эксперименте вместо значения искомого аналита C (концентрации) получается другая величина x (сигнал), связанная, но не равная C, т.е. x (C) ≠ С. Как правило, вид зависимости x (C) не известен, однако, к счастью, в аналитической химии большинство измерений пропорциональны. Это означает, что при увеличении концентрации С в a раз, сигнал X увеличится на столько же., т.е. x ( a C) = a x (C). Кроме того, сигналы еще и аддитивны, так что сигнал от пробы, в которой присутствуют два вещества с концентрациями C 1 и C 2 , будет равен сумме сигналов от каждого компонента, т.е. x (C 1 + C 2 ) = x (C 1 )+ x (C 2 ). Пропорциональность и аддитивность вместе дают линейность . Можно привести много примеров, иллюстрирующих принцип линейности, но достаточно упомянуть два самых ярких примера — хроматографию и спектроскопию. Вторая особенность, присущая эксперименту в аналитической химии — это многоканальность . Современное аналитическое оборудование одновременно измеряет сигналы для многих каналов. Например, измеряется интенсивность пропускания света сразу для нескольких длин волн, т.е. спектр. Поэтому в эксперименте мы имеем дело со множеством сигналов x 1 , x 2 . x n , характеризующих набор концентраций C 1 ,C 2 , . C m веществ, присутствующих в изучаемой системе.
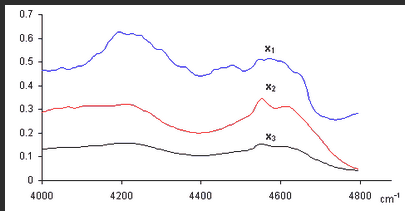
Итак, аналитический эксперимент характеризуется линейностью и многомерностью. Поэтому удобно рассматривать экспериментальные данные как векторы и матрицы и манипулировать с ними, используя аппарат матричной алгебры. Плодотворность такого подхода иллюстрирует пример, показанный на Рис. 1, где представлены три спектра, снятые для 200 длин волн от 4000 до 4796 cm −1 . Первый ( x 1 ) и второй ( x 2 ) спектры получены для стандартных образцов, в которых концентрация двух веществ A и B, известны: в первом образце [A] = 0.5, [B] = 0.1, а во втором образце [A] = 0.2, [B] = 0.6. Что можно сказать о новом, неизвестном образце, спектр которого обозначен x 3 ?
Рассмотрим три экспериментальных спектра x 1 , x 2 и x 3 как три вектора размерности 200. Средствами линейной алгебры можно легко показать, что x 3 = 0.1 x 1 +0.3 x 2 , поэтому в третьем образце очевидно присутствуют только вещества A и B в концентрациях [A] = 0.5×0.1 + 0.2×0.3 = 0.11 и [B] = 0.1×0.1 + 0.6×0.3 = 0.19.
Видео:А.7.35 Собственные вектора и собственные значения матрицыСкачать

1. Базовые сведения
Видео:НейроМаяк. Открытое рисование с Автором метода / Павел Пискарёв, D. Sc., Prof.Скачать

1.1 Матрицы
Матрицей называется прямоугольная таблица чисел, например
Матрицы обозначаются заглавными полужирными буквами ( A ), а их элементы — соответствующими строчными буквами с индексами, т.е. a ij . Первый индекс нумерует строки, а второй — столбцы. В хемометрике принято обозначать максимальное значение индекса той же буквой, что и сам индекс, но заглавной. Поэтому матрицу A можно также записать как < a ij , i = 1. I ; j = 1. J >. Для приведенной в примере матрицы I = 4, J = 3 и a 23 = −7.5.
Пара чисел I и J называется размерностью матрицы и обознается как I × J . Примером матрицы в хемометрике может служить набор спектров, полученный для I образцов на J длинах волн.
Видео:Овчинников А. В. - Линейная алгебра - Собственные значения и собственные векторы линейного оператораСкачать

1.2. Простейшие операции с матрицами
Матрицы можно умножать на числа. При этом каждый элемент умножается на это число. Например —
Рис. 3 Умножение матрицы на число
Две матрицы одинаковой размерности можно поэлементно складывать и вычитать. Например,
Рис. 4 Сложение матриц
В результате умножения на число и сложения получается матрица той же размерности.
Нулевой матрицей называется матрица, состоящая из нулей. Она обозначается O . Очевидно, что A + O = A , A − A = O и 0 A = O .
Матрицу можно транспонировать . При этой операции матрица переворачивается, т.е. строки и столбцы меняются местами. Транспонирование обозначается штрихом, A ‘ или индексом A t . Таким образом, если A = < a ij , i = 1. I ; j = 1. J >, то A t = < a ji , j = 1. J ; i = 1. I >. Например
Рис. 5 Транспонирование матрицы
Очевидно, что ( A t ) t = A , ( A + B ) t = A t + B t .
Видео:MATLAB 04 Массивы и матрицыСкачать

1.3. Умножение матриц
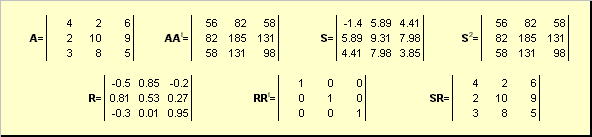
Матрицы можно перемножать, но только в том случае, когда они имеют соответствующие размерности. Почему это так, будет ясно из определения. Произведением матрицы A , размерностью I × K , и матрицы B , размерностью K × J , называется матрица C , размерностью I × J , элементами которой являются числа
Таким образом для произведения AB необходимо, чтобы число столбцов в левой матрице A было равно числу строк в правой матрице B . Пример произведения матриц —
Рис.6 Произведение матриц
Правило перемножения матриц можно сформулировать так. Для того, чтобы найти элемент матрицы C , стоящий на пересечении i -ой строки и j -ого столбца ( c ij ) надо поэлементно перемножить i -ую строку первой матрицы A на j -ый столбец второй матрицы B и сложить все результаты. Так в показанном примере, элемент из третьей строки и второго столбца, получается как сумма поэлементных произведений третьей строки A и второго столбца B
Рис.7 Элемент произведения матриц
Произведение матриц зависит от порядка, т.е. AB ≠ BA , хотя бы по соображениям размерности. Говорят, что оно некоммутативно. Однако произведение матриц ассоциативно. Это означает, что ABC = ( AB ) C = A ( BC ). Кроме того, оно еще и дистрибутивно, т.е. A ( B + C ) = AB + AC . Очевидно, что AO = O .
Видео:Відео 65. Знаходження власних чисел та векторів: прикладСкачать

1.4. Квадратные матрицы
Если число столбцов матрицы равно числу ее строк ( I = J = N ), то такая матрица называется квадратной. В этом разделе мы будем рассматривать только такие матрицы. Среди этих матриц можно выделить матрицы, обладающие особыми свойствами.
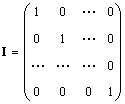
Единичной матрицей (обозначается I, а иногда E ) называется матрица, у которой все элементы равны нулю, за исключением диагональных, которые равны 1, т.е.
Очевидно AI = IA = A .
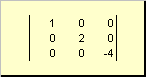
Матрица называется диагональной , если все ее элементы, кроме диагональных ( a ii ) равны нулю. Например
Рис. 8 Диагональная матрица
Матрица A называется верхней треугольной , если все ее элементы, лежащие ниже диагонали, равны нулю, т.е. a ij = 0, при i > j . Например
Рис. 9 Верхняя треугольная матрица
Аналогично определяется и нижняя треугольная матрица.
Матрица A называется симметричной , если A t = A . Иными словами a ij = a ji . Например
Рис. 10 Симметричная матрица
Матрица A называется ортогональной , если
Матрица называется нормальной если
Видео:Диагональный вид матрицы. Приведение матрицы к диагональному виду. Собственные векторыСкачать

1.5. След и определитель
Следом квадратной матрицы A (обозначается Tr( A ) или Sp( A )) называется сумма ее диагональных элементов,
Рис. 11 След матрицы
Sp(α A ) = α Sp( A ) и
Sp( A + B ) = Sp( A )+ Sp( B ).
Можно показать, что
Sp( A ) = Sp( A t ), Sp( I ) = N ,
Другой важной характеристикой квадратной матрицы является ее определитель (обозначается det( A )). Определение определителя в общем случае довольно сложно, поэтому мы начнем с простейшего варианта — матрицы A размерностью (2×2). Тогда
Для матрицы (3×3) определитель будет равен
В случае матрицы ( N × N ) определитель вычисляется как сумма 1·2·3· . · N = N ! слагаемых, каждый из которых равен
Индексы k 1 , k 2 . k N определяются как всевозможные упорядоченные перестановки r чисел в наборе (1, 2, . , N ). Вычисление определителя матрицы — это сложная процедура, которую на практике осуществляется с помощью специальных программ. Например,
Рис. 12 Определитель матрицы
Отметим только очевидные свойства:
det( I ) = 1, det( A ) = det( A t ),
det( AB ) = det( A )det( B ).
Видео:Работа с массивами. Вектор столбцы и вектор строки 1. Урок 7Скачать

1.6. Векторы
Если матрица состоит только из одного столбца ( J = 1), то такой объект называется вектором . Точнее говоря, вектором-столбцом. Например
Можно рассматривать и матрицы, состоящие из одной строки, например
Этот объект также является вектором, но вектором-строкой . При анализе данных важно понимать, с какими векторами мы имеем дело — со столбцами или строками. Так спектр, снятый для одного образца можно рассматривать как вектор-строку. Тогда набор спектральных интенсивностей на какой-то длине волны для всех образцов нужно трактовать как вектор-столбец.
Размерностью вектора называется число его элементов.
Ясно, что всякий вектор-столбец можно превратить в вектор-строку транспонированием, т.е.
В тех случаях, когда форма вектора специально не оговаривается, а просто говорится вектор, то имеют в виду вектор-столбец. Мы тоже будем придерживаться этого правила. Вектор обозначается строчной прямой полужирной буквой. Нулевым вектором называется вектор, все элементы которого раны нулю. Он обозначается 0 .
Видео:Собственные векторы и собственные значенияСкачать

1.7. Простейшие операции с векторами
Векторы можно складывать и умножать на числа так же, как это делается с матрицами. Например,
Рис. 13 Операции с векторами
Два вектора x и y называются колинеарными , если существует такое число α, что
Видео:18+ Математика без Ху!ни. Векторное произведение.Скачать

1.8. Произведения векторов
Два вектора одинаковой размерности N можно перемножить. Пусть имеются два вектора x = ( x 1 , x 2 . x N ) t и y = ( y 1 , y 2 . y N ) t . Руководствуясь правилом перемножения «строка на столбец», мы можем составить из них два произведения: x t y и xy t . Первое произведение
называется скалярным или внутренним . Его результат — это число. Для него также используется обозначение ( x , y ) = x t y . Например,
Рис. 14 Внутреннее (скалярное) произведение
называется внешним . Его результат — это матрица размерности ( N × N ). Например,
Рис. 15 Внешнее произведение
Векторы, скалярное произведение которых равно нулю, называются ортогональными .
Видео:Квантовая механика 8 - Операторы. Собственные векторы и собственные значения.Скачать

1.9. Норма вектора
Скалярное произведение вектора самого на себя называется скалярным квадратом. Эта величина
определяет квадрат длины вектора x . Для обозначения длины (называемой также нормой вектора) используется обозначение
Рис. 16 Норма вектора
Вектор единичной длины (|| x || = 1) называется нормированным. Ненулевой вектор ( x ≠ 0 ) можно нормировать, разделив его на длину, т.е. x = || x || ( x/ || x ||) = || x || e . Здесь e = x/ || x || — нормированный вектор.
Векторы называются ортонормированными, если все они нормированы и попарно ортогональны.
Видео:Урок 10 Собственные векторы и собственные значения матрицыСкачать

1.10. Угол между векторами
Скалярное произведение определяет и угол φ между двумя векторами x и y
Если вектора ортогональны, то cosφ = 0 и φ = π/2, а если они колинеарны, то cosφ = 1 и φ = 0.
Видео:Основы линейной алгебры. 2. Векторы. Часть 1Скачать

1.11. Векторное представление матрицы
Каждую матрицу A размера I × J можно представить как набор векторов
Здесь каждый вектор a j является j -ым столбцом, а вектор-строка b i является i -ой строкой матрицы A
1.12. Линейно зависимые векторы
Векторы одинаковой размерности ( N ) можно складывать и умножать на число, также как матрицы. В результате получится вектор той же размерности. Пусть имеется несколько векторов одной размерности x 1 , x 2 . x K и столько же чисел α α 1 , α 2 . α K . Вектор
y = α 1 x 1 + α 2 x 2 +. + α K x K
называется линейной комбинацией векторов x k .
Если существуют такие ненулевые числа α k ≠ 0, k = 1. K , что y = 0 , то такой набор векторов x k называется линейно зависимым . В противном случае векторы называются линейно независимыми. Например, векторы x 1 = (2, 2) t и x 2 = (−1, −1) t линейно зависимы, т.к. x 1 +2 x 2 = 0
1.13. Ранг матрицы
Рассмотрим набор из K векторов x 1 , x 2 . x K размерности N . Рангом этой системы векторов называется максимальное число линейно-независимых векторов. Например в наборе
имеются только два линейно независимых вектора, например x 1 и x 2 , поэтому ее ранг равен 2.
Очевидно, что если векторов в наборе больше, чем их размерность ( K > N ), то они обязательно линейно зависимы.
Рангом матрицы (обозначается rank( A )) называется ранг системы векторов, из которых она состоит. Хотя любую матрицу можно представить двумя способами (векторы столбцы или строки), это не влияет на величину ранга, т.к.
rank( A ) = rank( A t ).
1.14. Обратная матрица
Квадратная матрица A называется невырожденной, если она имеет единственную обратную матрицу A -1 , определяемую условиями
Обратная матрица существует не для всех матриц. Необходимым и достаточным условием невырожденности является
det( A ) ≠ 0 или rank( A ) = N .
Обращение матрицы — это сложная процедура, для выполнения которой существуют специальные программы. Например,
Рис. 17 Обращение матрицы
Приведем формулы для простейшего случая — матрицы 2×2
Если матрицы A и B невырождены, то
1.15. Псевдообратная матрица
Если матрица A вырождена и обратная матрица не существует, то в некоторых случаях можно использовать псевдообратную матрицу, которая определяется как такая матрица A + , что
Псевдобратная матрица — не единственная и ее вид зависит от способа построения. Например для прямоугольной матрицы можно использовать метод Мура-Пенроуза.
Если число столбцов меньше числа строк, то
A + =(A t A) −1 A t
Рис. 1 7a Псевдообращение матрицы
Если же число столбцов больше числа строк, то
A + =A t (AA t ) −1
1.16. Умножение вектора на матрицу
Вектор x можно умножать на матрицу A подходящей размерности. При этом вектор-столбец умножается справа Ax , а вектор строка — слева x t A . Если размерность вектора J , а размерность матрицы I × J то в результате получится вектор размерности I . Например,
Рис. 18 Умножение вектора на матрицу
Если матрица A — квадратная ( I × I ), то вектор y = Ax имеет ту же размерность, что и x . Очевидно, что
A (α 1 x 1 + α 2 x 2 ) = α 1 Ax 1 + α 2 Ax 2 .
Поэтому матрицы можно рассматривать как линейные преобразования векторов. В частности Ix = x , Ox = 0 .
2. Дополнительная информация
2.1. Системы линейных уравнений
Пусть A — матрица размером I × J , а b — вектор размерности J . Рассмотрим уравнение
относительно вектора x , размерности I . По сути — это система из I линейных уравнений с J неизвестными x 1 . x J . Решение существует в том, и только в том случае, когда
rank( A ) = rank( B ) = R ,
где B — это расширенная матрица размерности I ×( J+1 ), состоящая из матрицы A , дополненной столбцом b , B = ( A b ). В противном случае уравнения несовместны.
Если R = I = J , то решение единственно
Если R I , то существует множество различных решений, которые можно выразить через линейную комбинацию J − R векторов. Система однородных уравнений Ax = 0 с квадратной матрицей A ( N × N ) имеет нетривиальное решение ( x ≠ 0 ) тогда и только тогда, когда det( A ) = 0. Если R = rank( A ) N , то существуют N − R линейно независимых решений.
2.2. Билинейные и квадратичные формы
Если A — это квадратная матрица , а x и y — вектора соответствующей размерности, то скалярное произведение вида x t Ay называется билинейной формой , определяемой матрицей A . При x = y выражение x t Ax называется квадратичной формой.
2.3. Положительно определенные матрицы
Квадратная матрица A называется положительно определенной, если для любого ненулевого вектора x ≠ 0 ,
Аналогично определяются отрицательно ( x t Ax x t Ax ≥ 0) и неположительно ( x t Ax ≤ 0) определенные матрицы.
2.4. Разложение Холецкого
Если симметричная матрица A положительно определена, то существует единственная треугольная матрица U с положительными элементами, для которой
Рис. 19 Разложение Холецкого
2.5. Полярное разложение
Пусть A — это невырожденная квадратная матрица размерности N × N . Тогда существует однозначное полярное представление
где S — это неотрицательная симметричная матрица, а R — это ортогональная матрица. Матрицы S и R могут быть определены явно:
S 2 = AA t или S = ( AA t ) ½ и R = S −1 A = ( AA t ) −½ A .
Рис. 20 Полярное разложение
Если матрица A вырождена, то разложение не единственно — а именно: S по-прежнему одна, а вот R может быть много. Полярное разложение представляет матрицу A как комбинацию сжатия/растяжения S и поворота R .
2.6. Собственные векторы и собственные значения
Пусть A — это квадратная матрица. Вектор v называется собственным вектором матрицы A , если
где число λ называется собственным значением матрицы A . Таким образом преобразование, которое выполняет матрица A над вектором v , сводится к простому растяжению или сжатию с коэффициентом λ. Собственный вектор определяется с точностью до умножения на константу α ≠ 0, т.е. если v — собственный вектор, то и α v — тоже собственный вектор.
2.7. Собственные значения
У матрицы A , размерностью ( N × N ) не может быть больше чем N собственных значений. Они удовлетворяют характеристическому уравнению
являющемуся алгебраическим уравнением N -го порядка. В частности, для матрицы 2×2 характеристическое уравнение имеет вид
Рис. 21 Собственные значения
Набор собственных значений λ 1 . λ N матрицы A называется спектром A .
Спектр обладает разнообразными свойствами. В частности
det( A ) = λ 1 ×. ×λ N , Sp( A ) = λ 1 +. +λ N .
Собственные значения произвольной матрицы могут быть комплексными числами, однако если матрица симметричная ( A t = A ), то ее собственные значения вещественны.
2.8. Собственные векторы
У матрицы A , размерностью ( N × N ) не может быть больше чем N собственных векторов, каждый из которых соответствует своему собственному значению. Для определения собственного вектора v n нужно решить систему однородных уравнений
Она имеет нетривиальное решение, поскольку det( A − λ n I ) = 0.
Рис. 22 Собственные вектора
Собственные вектора симметричной матрицы ортогональны.
2.9. Эквивалентные и подобные матрицы
Две прямоугольные матрицы A и B одной размерности I × J эквивалентны , если существуют такие квадратные матрицы S , размерности I × I , и T , размерности J × J , что
Эквивалентные матрицы имею один и тот же ранг.
Две прямоугольные матрицы A и B одной размерности N × N подобны , если существует такая невырожденная матрица T , что
Матрица T называется преобразованием подобия.
Подобные матрицы имеют один и тот же ранг, след, определитель и спектр.
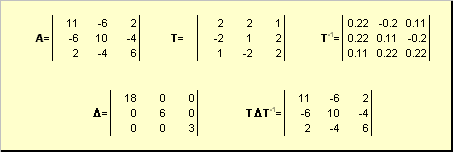
2.10. Приведение матрицы к диагональному виду
Нормальную (в частности симметричную) матрицу A можно привести к диагональному виду преобразованием подобия —
Здесь Λ = diag(λ 1 . λ N ) — это диагональная матрица, элементами которой являются собственные значения матрицы A , а T — это матрица, составленная из соответствующих собственных векторов матрицы A , т.е. T = ( v 1 . v N ).
Рис. 23 Приведение к диагональному виду
2.11. Разложение по сингулярным значениям (SVD)
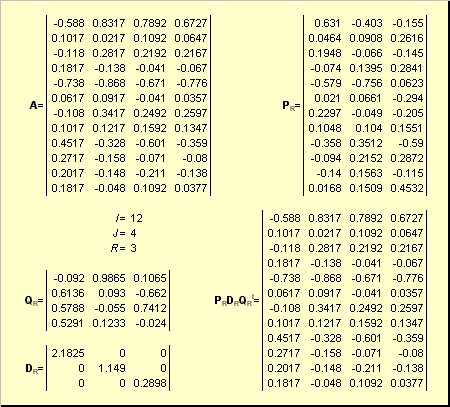
Пусть имеется прямоугольная матрица A размерностью I × J ранга R ( I ≤ J ≤ R ). Ее можно разложить в произведение трех матриц P R ( I × R ), D R ( R × R ) и Q R ( J × R ) —
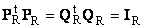
Здесь P R — матрица, образованная R ортонормированными собственными векторами p r матрицы AA t , соответствующим R наибольшим собственным значениям λ r ;
AA t p r = λ r p r ;
Q R — матрица, образованная R ортонормированными собственными векторами q r матрицы A t A ;
A t Aq r = λ r q r .
D R = diag (σ 1 . σ R ) — положительно определенная диагональная матрица , элементами которой являются σ 1 ≥. ≥σ R ≥0 — сингулярные значения матрицы A , равные квадратным корням из собственных значений матрицы A t A —
Рис. 24 SVD разложение
Дополняя матрицы P R и Q R ортонормированными столбцами, а матрицу D R нулевыми значениями, можно сконструировать матрицы P ( I × J ), D ( J × J ) и Q ( J × J ) такие, что
2.12. Линейное пространство
Рассмотрим все возможные векторы размерности N . Это множество называется линейным пространством размерности N и обозначается R N . Так как в R N включены все возможные векторы, то любая линейная комбинация векторов из R N будет также принадлежать этому пространству.
2.13. Базис линейного пространства
Любой набор из N линейно независимых векторов называется базисом в пространстве R N . Простейший пример базиса — это набор векторов
в каждом из которых только один элемент равен 1, а остальные равны нулю. Тогда любой вектор x = ( x 1 , x 2 . x N ) t может быть представлен как линейная комбинация x = x 1 e 1 + x 2 e 2+ . + x N e N базисных векторов.
Базис, составленный из попарно ортогональных векторов, называется ортогональным , а если базисные вектора еще и нормированы, то этот базис называется ортонормированным .
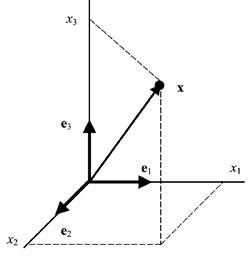
2.14. Геометрическая интерпретация
Линейному пространству можно дать удобную геометрическую интерпретацию. Представим себе N -мерное пространство, в котором базисные вектора задают направления осей координат. Тогда произвольный вектор x = ( x 1 , x 2 . x N ) t можно изобразить точкой в этом пространстве с координатами ( x 1 , x 2 . x N ).
Рис. 25 Координатное пространство
2.15. Множественность базисов
В линейном пространстве могут быть неограниченное число базисов. Так, в пространстве R 3 помимо обычного ортонормированного базиса
можно установить и другой ортонормированный базис, например
Каждый базис можно представить матрицей B = ( b 1 . b N ), составленной из базисных векторов. Переход от одного базиса к другому осуществляется с помощью невырожденной квадратной матрицы T , т.е. B 2 = TB 1 .
2.16. Подпространство
Пусть имеется набор из K линейно независимых векторов x 1 , x 2 . x K в пространстве R N . Рассмотрим все возможные линейные комбинации этих векторов
x = α 1 x 1 + α 2 x 2 +. + α K x K
О получившимся множестве Q говорят, что оно является линейной оболочкой или что оно натянуто на векторы x 1 , x 2 . x K . По определению линейного пространства это множество Q само является линейным пространством размерности K . При этом оно принадлежит пространству R N , поэтому Q называется линейным подпространством R K в пространстве R N .
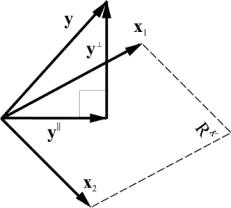
2.17. Проекция на подпространство
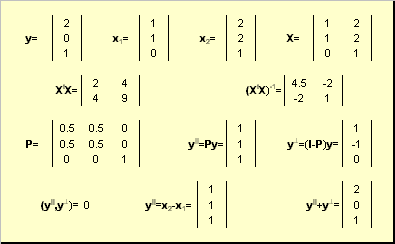
Рассмотрим подпространство R K , натянутое на векторы X = ( x 1 , x 2 . x K ) в пространстве R N . Матрица базиса X имеет размерность ( N × K ). Любой вектор y из R N может быть спроецирован на подпространство R K , т.е. представлен в виде
где вектор y || принадлежит R K , а вектор y ⊥ ортогонален y || .
Рис. 26 Проекция на подпространство
Проекцию y || можно представить как результат действия проекционной матрицы P
Проекционная матрица определяется как
Заключение
Матричные методы активно используются при анализе данных, в том числе и хемометрическими методами.