Собственные числа и собственные векторы матрицы.
Из курса линейной алгебры известно, что если А х = l х , то вектор х называется собственным вектором матрицы А , а число l – собственным числом, соответствующим данному собственному вектору. Совокупность всех собственных чисел матрицы называется спектром матрицы. Если в спектре матрицы одно и тоже собственное число встречается k раз, то говорят, что кратность этого собственного числа равна k .
Для нахождения собственных чисел матрицы А используется команда eigenvalues(A). Для нахождения собственных векторов матрицы А используется команда eigenvectors(A). В результате выполнения этой команды будут получены собственные числа, их кратность и соответствующие собственные векторы.
Чтобы понять, в каком виде получаются результаты выполнения команды eigenvectors, внимательно разберитесь со следующим примером: матрица 






В строке вывода перечислены в квадратных скобках собственное число, его кратность и соответствующий собственный вектор в фигурных скобках , затем следующие наборы таких же данных.
Характеристический и минимальный многочлены матрицы.
Для вычисления характеристического многочлена 
Минимальный многочлен (делитель) матрицы А можно найти с помощью команды minpoly(A,lambda).
Канонические и специальные виды матрицы.
Привести матрицу А к нормальной форме Жордана можно командой jordan(A).
К треугольному виду матрицу А можно привести тремя способами:
команда gausselim(A) приводит матрицу А к треугольному виду методом Гаусса;
команда ffgausselim(A) приводит матрицу А к треугольному виду методом Гаусса без деления. Эта команда предпочтительней для работы с символьными матрицами, так как не производит нормировку элементов и исключает возможные ошибки, связанные с делением на нуль;
команда gaussjord(A) приводит матрицу А к треугольному виду методом Гаусса-Жордана.
Характеристическую матрицу 
Видео:Собственные векторы и собственные числа линейного оператораСкачать

Задание 3.
- Дана матрица
. Найти ее собственные векторы и собственные числа.

Дана матрица 
 .
.
Привести матрицу А к Жордановой форме, треугольному виду, найти ее характеристическую матрицу.
Самостоятельно проверьте, чем будет отличаться результат выполнения команды ffgausselim(A) от gausselim(A) на этом примере.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Видео:Новые возможности Maple 2018 | New Features in Maple 2018Скачать

Описание пакета LinearAlgebra
Действия с матрицами
Определение матрицы.
Для определения матрицы в Maple можно использовать команду matrix(n, m, [[a11,a12,…,a1n], [a21,a22,…,a2m],…, [an1,an2,…,anm]]), где n — число строк, m – число столбцов в матрице. Эти числа задавать необязательно, а достаточно перечислить элементы матрицы построчно в квадратных скобках через запятую. Например:
В Maple матрицы специального вида можно генерировать с помощью дополнительных команд. В частности диагональную матрицу можно получить командой diag. Например:
> J:=diag(1,2,3);
Генерировать матрицу можно с помощью функции f(i, j) от переменных i, j – индексов матрицы: matrix(n, m, f), где где n — число строк, m – число столбцов. Например:
> f:=(i, j)->x^i*y^j;
>A:=matrix(2,3,f);
Число строк в матрице А можно определить с помощью команды rowdim(A), а число столбцов – с помощью команды coldim(A).
Арифметические операции с матрицами.
Сложение двух матриц одинаковой размерности осуществляется теми же командами, что и сложение векторов: evalm(A+B) или matadd(A,B). Произведение двух матриц может быть найдено с помощью двух команд:
- evalm(A&*B);
- multiply(A,B).
В качестве второго аргумента в командах, вычисляющих произведение, можно указывать вектор, например:
> B:=matrix([[-5,1], [7,4]]);
> v:=vector([2,4]);
> multiply(A,v);
> multiply(A,B);
> matadd(A,B);
Команда evalm позволяет также прибавлять к матрице число и умножать матрицу на число. Например:
> С:=matrix([[1,1],[2,3]]):
> evalm(2+3*С);
Определители, миноры и алгебраические дополнения. Ранг и след матрицы.
Определитель матрицы А вычисляется командой det(A).Команда minor(A,i,j) возвращает матрицу, полученную из исходной матрицы А вычеркиванием i-ой строки и j-ого столбца. Минор Mij элемента aij матрицы А можно вычислить командой det(minor(A,i,j)).Ранг матрицы А вычисляется командой rank(A). След матрицы А, равный сумме ее диагональных элементов, вычисляется командой trace(A).7
>det(A);
> minor(А,3,2);
> det(%);
> trace(A);
Обратная и транспонированная матрицы.
Обратную матрицу А- 1 , такую что А- 1 А=АА- 1 =Е, где Е — единичная матрица, можно вычислить двумя способами:
- evalm(1/A);
- inverse(A).
Транспонирование матрицы А – это изменение местами строк и столбцов. Полученная в результате этого матрица называется транспонированной и обозначается А’. Транспонированную матрицу А’ можно вычислить командой transpose(A).
Например, используя заданную в предыдущем пункте матрицу А, найдем ей обратную и транспонированную:
>inverse(A);
> multiply(A,%);
> transpose(A);
Выяснение типа матрицы.
Выяснить положительную или отрицательную определенность матрицы можно при помощи команды definite(A,param), где param может принимать значения: ‘positive_def’ – положительно определена (A>0), ‘positive_semidef’ – неотрицательно определенная 
> definite(А,’positive_def’);
Проверить ортогональность матрицы А можно командой orthog(A).
> В:=matrix([[1/2,1*sqrt(3)/2],
[1*sqrt(3)/2,-1/2]]);
> orthog(В);
Функции от матриц.
Возведение матрицы А в степень n производится командой evalm(A^n). Вычисление матричной экспоненты 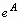
> exponential(Т);
> evalm(Т^2);
Задание 2.
- Даны матрицы:
,
,
. Найти: (AB)C , detA, detB, detC, det[(AB)C]. Наберите:
> with(linalg):restart;
> A:=matrix([[4,3],[7,5]]):
> B:=matrix([[-28,93],[38,-126]]):
> C:=matrix([[7,3],[2,1]]):
> Det(A)=det(A); Det(B)=det(B); Det(C)=det(C);
Det(F)=det(F);
- Дана матрица
, найти: detA,
, A’, det(M22). Наберите:
> Det(A)=det(A);
> transpose(A);
> inverse(A);
> det(minor(A,2,2));
- Найти ранг матрицы
.
> A:=matrix([[8,-4,5,5,9], [1,-3,-5,0,-7],
> r(A)=rank(A);
- Вычислить
, где
.
> exponential([[3,-1],[1,1]]);
- Дана матрица
. Найти значение многочлена
.
> P(A)=evalm(A^3-18*A^2+64*A);
Описание пакета LinearAlgebra
В Maple имеется пакет LinearAlgebra, ориентированный на решение задач линейной (матричной) алгебры. Он загружается соответствующей командой:
[> with(LinearAlgebra);
После выполнения этих команд система выводит на экран список процедур и функций, которыми располагает пакет LinearAlgebra.
Пакет LinearAlgebra является более мощным и совершенным по сравнению с linalg (в ранних версиях программы). Он предназначен для работы с матрицами и векторами больших размеров. Самым простым образом матрицу 
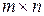
Приведем в табл. 3.1 назначение наиболее часто применимых процедур и функций пакета LinearAlgebra. Более полную информацию о каждой процедуре или функции можно узнать в справке, или набрав команду
[> help(имя_процедуры);
| Название процедуры, функции | Формат команды | Назначение процедуры, функции |
| Matrix | [> Matrix(m, n, [[a[1,1],…,a[1,n]],…,[a[m,1],…,a[m,n]]]); | Формирование матрицы |
| Basis | Определяет базис для векторного пространства, заданного системой векторов | |
| CharacteristicMatrix | Создает для квадратной матрицы ее характеристическую матрицу | |
| CharacteristicPolynomial | Создает для квадратной матрицы ее характеристический многочлен | |
| Determinant | Вычисляет для квадратной матрицы ее определитель | |
| DiagonalMatrix | Создает диагональную матрицу | |
| Eigenvalues | Вычисляет для квадратной матрицы ее собственные значения (собственные числа) | |
| Eigenvectors | Вычисляет для квадратной матрицы ее собственные векторы (рекомендуется использовать вместе с процедурой Eigenvalues) | |
| LinearSolve | Решает систему линейных алгебраических уравнений (СЛАУ) в матричной форме | |
| MatrixAdd | Процедура сложения двух матриц | |
| Matrixlnverse | Процедура нахождения обратной матрицы | |
| MatrixMatrixMultiply | Процедура произведения двух матриц | |
| MatrixNorm | Функция вычисления нормы матрицы | |
| MatrixScalarMultiply | Процедура умножения матрицы на скаляр | |
| MatrixVectorMultiply | Процедура умножения матрицы на вектор | |
| Minor | Вычисляет минор матрицы | |
| Normalize | Нормализует вектор | |
| NullSpace | Возвращает нуль-пространство (ядро) матрицы | |
| Rank | Вычисляет ранг матрицы | |
| SylvesterMatrix | Конструирует матрицу Сильвестра из многочленов | |
| Transpose | Вычисляет матрицу, транспонированную к данной |
Пример 3.1. Исследовать СЛАУ с параметром 

Ниже приведен текст рабочего листа по решению данной задачи (с описаниями по ходу выполнения команд).
[> restart; with(LinearAlgebra): /задаем вектор-столбцы основной матрицы/ [> a1:=Vector([2,1,3]); a2:=Vector([lambda+1,lambda,-3]); a3:=Vector([lambda-2,-3,-7]);  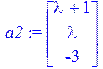 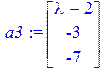 /задаем основную матрицу и вектор-столбец свободных коэффициентов системы/ [> A:=Matrix(3,3,[a1,a2,a3]); B:=Vector([3,lambda+2,3]); /задаем основную матрицу и вектор-столбец свободных коэффициентов системы/ [> A:=Matrix(3,3,[a1,a2,a3]); B:=Vector([3,lambda+2,3]); 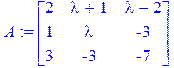  /выводим определитель основной матрицы системы, решение системы в матричном виде (при значениях, в которых определитель основной матрицы не равен нулю)/ [> Delta:=Determinant(A); X:=LinearSolve(A,B); /выводим определитель основной матрицы системы, решение системы в матричном виде (при значениях, в которых определитель основной матрицы не равен нулю)/ [> Delta:=Determinant(A); X:=LinearSolve(A,B);   /вычисляем значения параметра /вычисляем значения параметра  , при котором определитель обращается в нуль/ [> Korni:=solve(Determinant(A)=0); , при котором определитель обращается в нуль/ [> Korni:=solve(Determinant(A)=0);  [> lambda:=Korni[1]; X:=LinearSolve(A,B); [> lambda:=Korni[1]; X:=LinearSolve(A,B);  Error,(in LinearAlgebra:-LA_Main:-LinearSolve) inconsistent system /Maple предупреждает, что СЛАУ при данном значении параметра Error,(in LinearAlgebra:-LA_Main:-LinearSolve) inconsistent system /Maple предупреждает, что СЛАУ при данном значении параметра  несовместна/ [> lambda:=Korni[2]; X:=LinearSolve(A,B); /СЛАУ имеет бесконечное множество решений при этом значении параметра несовместна/ [> lambda:=Korni[2]; X:=LinearSolve(A,B); /СЛАУ имеет бесконечное множество решений при этом значении параметра  / /   |
Пример 3.2. Найти собственные числа и соответственные собственные векторы матрицы

Текст рабочего листа по решению задачи имеет вид:
Видео:Программирование в Maple 2017 | Programming in Maple 2017Скачать

Линейная алгебра
Искусство использования матриц и векторов для решения задач физики
Видео:Новые возможности Maple 2023!Скачать

Собственные значения
и собственные векторы
Одно из наиболее важных применений линейной алгебры в физике – это собственные значения и собственные векторы. Они есть в математической физике, классической механике, квантовой механике, численном анализе. В применении к матрицам задача о собственных значениях выглядит так.
Дана квадратная матрица A. Какими должны быть векторы x j и числа λ j , чтобы при умножении A на x j получался вектор x j , умноженный на число λ j ?
Существуют ли такие x j и λ j , что можно записать:
Поскольку умножение матрицы на вектор одновременно вращает вектор и умножает его на число, неясно, есть ли решение у этой задачи. Но можно доказать, что в большинстве случаев для матрицы размером 
Если собственный вектор x j умножается на A, то результат есть вектор, который либо параллелен x j (если λ j положительно), либо противоположно направлен (если λ j отрицательно).
Простая иллюстрация этой идеи:
OК, ясно, что получено «нечто вроде». Обычно нужны числа, а не гигантские абстрактные выражения. Простой путь их получения – ввести в матрицу элементы в виде чисел с плавающей запятой, т. е. с десятичной точкой:
Это намного лучше.
Теперь посмотрим на выдачу.
Из справки Maple help для Eigenvectors :
Первый набор чисел – это вектор-столбец, содержащий числа – собственные значения, а второй набор – это матрица, столбцы которой есть собственные векторы.
Поэтому если нужно получить третье собственное значение, то следует записать:
(Это выглядит странным, но так как v[1] – это вектор-столбец, имеет смысл спрашивать о его третьем элементе [3] .) Теперь нам нужен третий столбец v[2] , это делает команда Maple Column .
Теперь, умножая v3 на A , можно проверить, действительно ли это собственный вектор. Если так, то 
Для проверки правильности разделим y на λ 3 и посмотрим, получается ли собственный вектор 
Если в матрице, созданной Eigenvector , сравнить этот вектор с 
Поверните матрицу Rx из задачи о повороте вектора и найдите ее собственные значения и собственные векторы. Подумайте, что означает вращение и можно ли дать физический смысл ответам, полученным из Maple. При выборе значения theta попробуйте:
(b) θ = 
(c) θ = 
(Учтите, что (c) понадобится при изучении спина в квантовой механике.) Хороший способ решить эту задачу – определить матрицу Rx с помощью функции Maple M(θ)
и затем применить ее для вычисления трех матриц в заданиях (a)–(c). (Из-за того, что в Maple10 есть ошибка, не стоит использовать в задаче evalf .)
Если трехкомпонентные векторы поворачиваются матрицей вращения, то матрицы 
(a) Создайте диагональную матрицу 
Назовите новую матрицу M2.
(b) Вычислите собственные значения и собственные векторы матриц M1 и M2. Как их сравнить?
(c) Умножьте с обеих сторон M1 на вектор 
📺 Видео
Решение системы линейных уравнений в MapleСкачать

Начало работы с Maple 2017 | Getting Started with Maple 2017Скачать

Learning Maple: Vectors 1 - Cartesian CoordinatesСкачать

Интерактивная математика в Maple 2017 | Clickable Math in Maple 2017Скачать

Maple Учимся рисовать в программеСкачать

Модель Леонтьева в программе MapleСкачать

18+ Математика без Ху!ни. Векторное произведение.Скачать

Курс лекций "Линейная алгебра". Часть 6: Собственные числа и собственные векторыСкачать

Компланарны ли векторы: a=(2;5;8), b=(1;-3;-7) и c=(0;5;10)?Скачать

Exercises of vectors, forces and moment with Maple part #01Скачать

Maple: Lab Session 5Скачать

 . Найти ее собственные векторы и собственные числа.
. Найти ее собственные векторы и собственные числа.














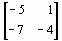












 ,
,  ,
,  . Найти: (AB)C , detA, detB, detC, det[(AB)C]. Наберите:
. Найти: (AB)C , detA, detB, detC, det[(AB)C]. Наберите:
 , найти: detA,
, найти: detA,  , A’, det(M22). Наберите:
, A’, det(M22). Наберите:


 .
. , где
, где  .
.
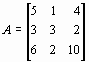 . Найти значение многочлена
. Найти значение многочлена  .
.


