Гипотенуза прямоугольного треугольника 45 градусов

Видео:Как найти гипотенузу в прямоугольном треугольнике, минуя теорему Пифагора?Скачать

Онлайн калькулятор

Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):

• для гипотенузы (с):
  • длины катетов a и b
  • длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
  • длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
• для катета:
  • длину гипотенузы (с) и длину одного из катетов
  • длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
  • длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
  • длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
  • длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)

Введите их в соответствующие поля и получите результат.

Найти гипотенузу (c)

Найти гипотенузу по двум катетам

Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?

Формула

следовательно: c = √ a² + b²

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:

c = √ 3² + 4² = √ 9 + 16 = √ 25 = 5 см

Найти гипотенузу по катету и прилежащему к нему острому углу

Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?

Формула

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:

c = 2 / cos(60) = 2 / 0.5 = 4 см

Найти гипотенузу по катету и противолежащему к нему острому углу

Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?

Формула

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:

c = 2 / sin(30) = 2 / 0.5 = 4 см

Найти гипотенузу по двум углам

Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.

Найти катет

Найти катет по гипотенузе и катету

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?

Формула

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:

a = √ 5² — 4² = √ 25 — 16 = √ 9 = 3 см

Найти катет по гипотенузе и прилежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?

Формула

Пример

Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:

b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см

Найти катет по гипотенузе и противолежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?

Формула

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:

a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см

Найти катет по второму катету и прилежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?

Формула

Пример

Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:

b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см

Найти катет по второму катету и противолежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?

Формула

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:

Видео:Теорема Пифагора для чайников)))Скачать

Расчёт катетов по гипотенузе и углу

Прямоугольный треугольник это треугольник у которого один из углов равен 90 градусов.

Прямой угол это угол 90 градусов.

Гипотенуза это противолежащая прямому углу сторона, самая длинная сторона прямоугольного треугольника.

Катеты это стороны прямоугольного треугольника прилежащие к прямому углу.

Сумма внутренних углов треугольника равна 180 градусам.

Синусом называется отношение противолежащего катета к гипотенузе.

Косинусом называется отношение прилежащего катета к гипотенузе.

Видео:В прямоугольном треугольнике гипотенуза равна 6 ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

Гипотенуза и угол «α» прямоугольного треугольника

Видео:Определение длины гипотенузыСкачать

Свойства

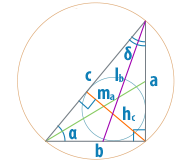
Если в прямоугольном треугольнике известна гипотенуза и угол α, то можно сразу вычислить катеты и угол β из свойства суммы углов треугольника и отношений синуса и косинуса. (рис. 79.1) β=90°-α a=c sin⁡α b=c cos⁡α

Периметр, заданный суммой катетов и гипотенузы, можно представить в виде суммы известной гипотенузы и выраженных через нее катетов. P=a+b+c=c sin⁡α+c cos⁡α+c=c(sin⁡α+cos⁡α+1)

Площадь любого прямоугольного треугольника равна половине произведения катетов, следовательно, чтобы рассчитать площадь через гипотенузу и угол α, необходимо также заменить неизвестные на соответствующие выражения. S=ab/2=(sin⁡α cos⁡α)/2

Треугольник, в котором один угол прямой, будет иметь всего одну высоту, опущенную на гипотенузу. Из любого внутреннего прямоугольного треугольника, полученного с помощью дополнительного построения высоты, можно выразить ее, как произведение катета и синуса угла. (рис. 79.2) h=b sin⁡α=c cos⁡α sin⁡α

Найти медиану прямоугольного треугольника проще всего, если она опущена на гипотенузу, в таком случае она будет равна ее половине. Медианы катетов вычисляются по стандартным формулам с заменой переменных через гипотенузу. (рис.79.3) m_с=c/2 m_b=√(2a^2+2c^2-b^2 )/2=√(2a^2+2a^2+2b^2-b^2 )/2=√(4a^2+b^2 )/2=√(4 〖c^2 sin^2〗⁡α+〖c^2 cos^2〗⁡α )/2=(с√(3 sin^2⁡α+1))/2 m_a=√(2c^2+2b^2-a^2 )/2=√(2a^2+2b^2+2b^2-a^2 )/2=√(4 〖c^2 cos〗^2⁡α+sin^2⁡α )/2=(с√(3 cos^2⁡α+1))/2

Рассчитать биссектрисы прямоугольного треугольника тоже достаточно просто, если использовать специальные формулы, зная гипотенузу и угол α. Преобразуя выражения, можно упростить их до следующих тождеств. (рис. 79.4) l_с=(ab√2)/(a+b)=(c sin⁡α cos⁡α √2)/(sin⁡α+cos⁡α ) l_a=√(bc(a+b+c)(b+c-a) )/(b+c)=√(bc((b+c)^2-a^2 ) )/(b+c)=√(bc(b^2+2bc+c^2-a^2 ) )/(b+c)=√(bc(b^2+2bc+b^2 ) )/(b+c)=√(bc(2b^2+2bc) )/(b+c)=(b√(2c(b+c) ))/(b+c)=(c cos⁡α √(2c(c cos⁡α+c) ))/(c cos⁡α+c)=(c cos⁡α √(2(cos⁡α+1) ))/(cos⁡α+1) l_b=√(ac(a+b+c)(a+c-b) )/(a+c)=(a√(2c(a+c) ))/(a+c)=(c sin⁡α √(2c(c sin⁡α+c) ))/(c sin⁡α+c)=(c sin⁡α √(2(sin⁡α+1) ))/(sin⁡α+1)

Проведенная средняя линия прямоугольного треугольника создает внутри него еще один подобный треугольник в два раза меньше первоначального, поэтому сама она равна половине параллельной ей стороны. (рис. 79.7) M_a=a/2=(c sin⁡α)/2 M_b=b/2=(c cos⁡α)/2 M_c=c/2

Прямоугольный треугольник может быть вписан в окружность и описан вокруг нее. Радиус вписанной окружности внутри треугольника можно вычислить, сложив катеты за вычетом гипотенузы, и разделив полученное число на два. Рассчитать радиус описанной окружности для прямоугольного треугольника через гипотенузу еще проще, так как он равен ее половине. (рис. 79.5, 79.6) r=(a+b-c)/2=(c sin⁡α+c cos⁡α-c)/2=c/2 (sin⁡α+cos⁡α-1) R=c/2

📹 Видео

Треугольники с углами 45, 45 и 90 градусовСкачать

ЗНАЧЕНИЯ СИНУСА, КОСИНУСА И ТАНГЕНСА 30, 45 И 60 ГРАДУСОВСкачать

7 кл г. Теорема: «катет лежавший напротив угла в 30 градусов равен половине гипотенузы»Скачать

Найдите гипотенузу равнобедренного прямоугольного треугольника, площадь которого равна 1Скачать

Нахождение стороны прямоугольного треугольникаСкачать

Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Решение прямоугольных треугольниковСкачать

Задача по геометрии на прямоугольный треугольник и теорему Пифагора из реального ОГЭ по математикеСкачать

Геометрия Синус.Чему равен синус 30,45,60 градусов?Вывод табличных значений.Скачать

Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать

№256. Один из углов прямоугольного треугольника равен 60°, а сумма гипотенузы и меньшего из катетовСкачать

Свойства прямоугольного треугольника. 7 класс.Скачать

Гипотенуза прямоугольного треугольникаСкачать

№171. Гипотенуза прямоугольного равнобедренного треугольника лежит в плоскостиСкачать

ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать

В прямоугольном треугольнике один из катетов равен 10 ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать