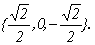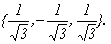Собственные векторы симметричной матрицы

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Страница — в разработке. Начало работ — 08.03.2014, окончание — .

Видео:Собственные векторы и собственные числа линейного оператораСкачать

Симметричная матрица

Теорема. Для любой матрицы $ A_ $ матрицы $ A_A^ $ и $ A^ A $ — симметричны. Для любой квадратной матрицы $ A_ $ матрица $ A_+A^ $ — симметрична.

Видео:Собственные векторы и собственные значения матрицыСкачать

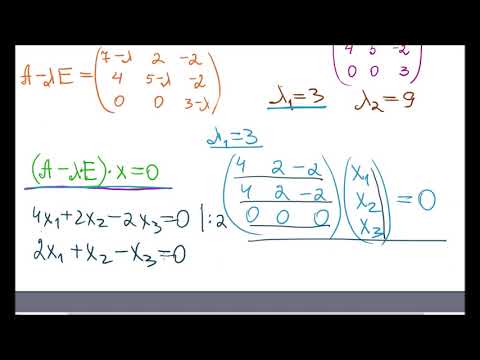
Определитель

Теорема [Кэли]. В полном разложении определителя симметричной матрицы порядка $ n $ обозначим $ mathfrak s_n $ число слагаемых, $ mathfrak s_n^ $ — число слагаемых с положительным знаком, $ mathfrak s_n^ $ — число слагаемых с отрицательным знаком, а $ mathfrak d_n =mathfrak s_n^ — mathfrak s_n^ $. Имеют место соотношения:

$$ mathfrak s_=(n+1)mathfrak s_n- C_n^2 mathfrak s_ ; $$ $$ mathfrak d_=-(n-1)mathfrak d_n- C_n^2 mathfrak d_ . $$

Имеют место пределы:

Миноры: тождества Кронекера

Теорема [Кронекер]. Для симметричной матрицы $ A_ $ порядка $ n ge k+1 $ имеет место тождество

$$ Aleft(begin 1 & 2 & dots & k-2 & k \ 2 & 3 & dots & k-1 & k+1 end right)- Aleft(begin 2 & 3 & dots & k-1 & k \ 1 & 2 & dots & k-2 & k+1 end right)= $$ $$ = Aleft(begin 1 & 2 & dots & k-3 & k-2 & k-1 \ 2 & 3 & dots & k-2 & k & k+1 end right) , $$ связывающее три ее минора порядка $ k-1 $.

Пример. Для $ k=4 $:

$$ Aleft(begin 1 & 2 & 4 \ 2 & 3 & 5 end right)- Aleft(begin 2 & 3 & 4 \ 1 & 2 & 5 end right)= Aleft(begin 1 & 2 & 3 \ 2 & 4 & 5 end right) $$ $$ iff left| begin a_ & a_ & a_ \ a_ & a_ & a_ \ a_ & a_ & a_ end right|- left| begin a_ & a_ & a_ \ a_ & a_ & a_ \ a_ & a_ & a_ end right|= left| begin a_ & a_ & a_ \ a_ & a_ & a_ \ a_ & a_ & a_ end right| . $$

В настоящем разделе минор матрицы $ A $ $$ Aleft( begin j_1 & dots & j_k \ j_1 & dots & j_k end right) = left|begin a_ & a_ & dots & a_ \ a_ & a_ & dots & a_ \ vdots & & ddots & vdots \ a_ & a_ & dots & a_ end right| , quad 1le j_1 ☞ ЗДЕСЬ.

Теорема. Если $ mathfrak r = operatorname (A)ge 1 $, то в матрице $ A $ существует ненулевой ведущий минор порядка $ mathfrak r $.

Видео:Собственные значения и собственные векторы матрицы (4)Скачать

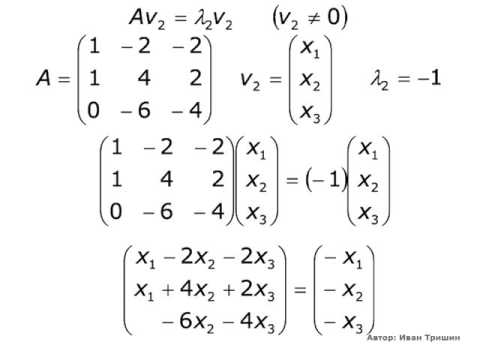
Произведение

Теорема. Для того, чтобы произведение симметричных матриц $ A $ и $ B $ было симметричной матрицей необходимо и достаточно, чтобы матрицы $ A $ и $ B $ коммутировали: $ AB = BA $.

Видео:А.7.40 Метод Якоби поиска собственных векторов и значений симметричных матрицСкачать

Обратная матрица

Теорема. Обратная к симметричной матрице (если существует) будет симметричной матрицей.

Видео:Диагональный вид матрицы. Приведение матрицы к диагональному виду. Собственные векторыСкачать

Характеристический полином, собственные числа, собственные векторы

Теорема 1. Все собственные числа симметричной матрицы вещественны.

Доказательство ☞ ЗДЕСЬ.

Если $ lambda=0 $ корень кратности $ mathfrak m $ характеристического полинома симметричной матрицы $ A $, т.е.

$$ det (A-lambda E)equiv(-1)^n lambda^n+a_1lambda^+dots+a_ lambda^ quad npu a_ne 0 $$ то $ operatorname (A)=n-mathfrak m $.

Если в характеристическом полиноме некоторый коэффициент $ a_j $ при $ j notin $ обращается в нуль, то соседние с ним в нуль не обращаются и имеют различные знаки: $ a_ a_ ♦

Локализация собственных чисел

Теорема [Коши]. Для симметричной матрицы $ A_ $ число ее собственных чисел, лежащих на интервале $ ]a,b_[ $, определяется по формуле:

Согласно этой теореме, главные миноры матрицы $ A-lambda, E $ играют роль системы полиномов Штурма для характеристического полинома симметричной матрицы $ A_ $.

$$ A_1,A_2,dots,A_ $$ симметричной матрицы $ A_ $ отличны от нуля, то число положительных собственных чисел матрицы $ A_ $ равно числу знакопостоянств, а число отрицательных собственных чисел — числу знакоперемен в ряду $ 1,A_1,dots,A_n $:

Часто в приложениях требуется вычислить значения не всех собственных чисел симметричной матрицы, а только небольшого (по сравнению с порядком матрицы) количества максимальных по модулю. Численный метод решения этой задачи изложен ☞ ЗДЕСЬ.

Видео:Собственные векторы и собственные числа линейного оператораСкачать

Диагонализуемость

Теорема. Существует ортогональная матрица $ P_ $, приводящая симметричную матрицу $ A_ $ к диагональному виду:

$$ P^AP=P^<^>AP= left( begin lambda_1 & & & mathbb O \ & lambda_2 & & \ && ddots & \ mathbb O&& & lambda_n end right). $$

Доказательство особенно просто в случае когда все собственные числа $ lambda_1,dots, lambda_n $ различны. На основании теоремы 1 матрица $ A_ $ диагонализуема над множеством вещественных чисел и на основании теоремы 2 матрица $ P $, приводящая к диагональному виду, может быть выбрана ортогональной.

Для общего случая доказательство производится индукцией по порядку $ n $ матрицы $ A $. Окончание доказательства ☞ ЗДЕСЬ. ♦

Теорема утверждает что даже при наличии кратных корней у характеристического полинома $$ f(lambda)=(-1)^n(lambda — lambda_1)^<_1> times dots times (lambda — lambda_)^<_>, quad _1+dots+_<>=n, lambda_k ne lambda_ npu k ne ell $$ алгебраическая кратность собственного числа $ lambda_j $ совпадает с его геометрической кратностью: $$operatorname , (A-lambda_j, E)= _j, npu quad forall jin .$$ Или, что то же: размерность собственного подпространства $$ left <Xin mathbb R^n , big| , (A-lambda_j, E)X=mathbb O_right> $$ равна $ _j $. При нахождении фундаментальной системы решений (ФСР) указанной системы уравнений мы получим $ _j $ линейно независимых собственных векторов $ <_,dots, _<j_j> > $ , принадлежащих $ lambda_j $. Однако при традиционных способах построения ФСР вовсе не гарантирована ортогональность этих векторов. Как построить ФСР так, чтобы она удовлетворяла условию теоремы, т.е. была ортонормированной? Воспользуемся для этого процессом ортогонализации Грама-Шмидта, применив его к системе $ <_,dots, _<j_j> > $. Результатом процесса будет новая система векторов $ <_,dots, _<j _j> > $ такая что ее линейная оболочка совпадает с линейной оболочкой исходной системы: $$ left(_,dots, _<j _j> right)= left(_,dots, _<j_j> right) quad mbox quad langle _,_ rangle =0 mbox k ne ell , , $$ т.е. векторы $ _,dots, _<j _j> $ остаются собственными векторами, принадлежащими $ lambda_j $. Но теперь эти новые векторы попарно ортогональны. Нормировав их, мы получим требуемую теоремой систему из $ _j $ ортогонормированных столбцов матрицы $ P $, соответствующих кратному собственному числу $ lambda_j $.

Пример. Диагонализовать матрицу

$$ A=left( begin 0&1&0&1&0&0&0&-1 \ 1&0&1&0&0&0&-1&0 \ 0&1&0&1&0&-1&0&0 \ 1&0&1&0&-1&0&0&0 \ 0&0&0&-1&0&1&0&1 \ 0&0&-1&0&1&0&1&0 \ 0&-1&0&0&0&1&0&1 \ -1&0&0&0&1&0&1&0 end right) $$ с помощью ортогональной матрицы.

Решение. Имеем: $$ det (A-lambda E) equiv (lambda-3)(lambda+3)(lambda-1)^3(lambda+1)^3 , . $$ Ищем собственные векторы. Для простых собственных чисел: $$ lambda_1=-3 Rightarrow mathfrak X_1=left[1,-1,1,,-1,-1,1,-1,1right]^ ; $$ $$ lambda_2=3 Rightarrow mathfrak X_2=left[-1,-1,-1,-1,1,1,1,1right]^ . $$ Эти столбцы войдут в состав матрицы $ P $, только их надо нормировать: $ mathfrak X_ /|mathfrak X_| $. Для кратных собственных чисел $ lambda_j in $ сначала находим произвольные ФСР $$ lambda_3=1 Rightarrow left<begin x_1&-x_2 & &-x_4 & & & &+x_8 & =0 \ & x_2 &-x_3 & +x_4 & & -x_6 & & & =0 \ & & x_3 & +x_4 & & & -x_7 &-x_8& =0 \ & & & 3,x_4 &+x_5 & -x_6 & -2,x_7 & -x_8 & =0 \ & & & & x_5 & -x_6 & +x_7 & -x_8 & =0 end right. $$ $$ Rightarrow mathfrak X_ =left[1,1,0,0,1,1,0,0 right]^ ;mathfrak X_ =left[ 0,-1,0,1,-1,0,1,0 right]^; mathfrak X_ =left[0,1,1,0,1,0,0,1 right]^ . $$ $$ lambda_4=-1 Rightarrow quad left< begin mathfrak X_ =left[-1,1,0,0,-1,1,0,0 right]^\ mathfrak X_ =left[ 0,1,-1,0,-1,0,0,1 right]^ \ mathfrak X_ =left[0,1,0,-1,-1,0,1,0 right]^ end right>, . $$ Применяем к каждой из них алгоритм ортогонализации Грама-Шмидта: $$mathfrak Y_=mathfrak X_=left[1,1,0,0,1,1,0,0 right]^; $$ $$ mathfrak Y_=mathfrak X_+ <coloralpha > mathfrak Y_, quad langle mathfrak Y_,mathfrak Y_ rangle =0 quad Rightarrow <coloralpha >=-frac<langle mathfrak X_,mathfrak Y_ rangle><langle mathfrak Y_,mathfrak Y_ rangle >=frac quad Rightarrow $$ $$ Rightarrow mathfrak Y_=left[frac,-frac,0,1,-frac,frac,1,0 right]^ ; $$ $$ mathfrak Y_=mathfrak X_+ <colorbeta > mathfrak Y_+ <colorgamma > mathfrak Y_, quad langle mathfrak Y_,mathfrak Y_ rangle =0, langle mathfrak Y_,mathfrak Y_ rangle =0 quad Rightarrow $$ $$ <colorbeta > =-frac<langle mathfrak X_,mathfrak Y_ rangle><langle mathfrak Y_,mathfrak Y_ rangle>=-frac, <colorgamma > =-frac<langle mathfrak X_,mathfrak Y_ rangle ><langle mathfrak Y_,mathfrak Y_ rangle >=frac quad Rightarrow $$ $$ Rightarrow mathfrak Y_=left[-frac,frac,1,frac,frac,-frac,frac,1 right]^ , . $$ $$ mathfrak Y_=mathfrak X_=left[-1,1,0,0,-1,1,0,0 right]^, mathfrak Y_=left[frac,frac,-1,0,-frac,-frac,0,1 right]^, $$ $$ mathfrak Y_=left[frac,frac,frac,-1,-frac,-frac,1,-frac right]^ , . $$ После нормирования, составляем из этих векторов ортогональную матрицу: $$ P= left(begin -sqrt/4 & sqrt/4 & 1/2 & sqrt/6 & -sqrt/12 & -1/2 & sqrt/6 & sqrt/12 \ -sqrt/4 & -sqrt/4 & 1/2 & -sqrt/6 & sqrt/12 & 1/2 & sqrt/6 & sqrt/12 \ -sqrt/4 & sqrt/4 & 0 & 0 & sqrt/4 & 0 & -sqrt/3 & sqrt/12 \ -sqrt/4 & -sqrt/4 & 0 & sqrt/3 & sqrt/12 & 0 & 0 & -sqrt/4 \ sqrt/4 & -sqrt/4 & 1/2 & -sqrt/6 & sqrt/12 & -1/2 & -sqrt/6 & -sqrt/12 \ sqrt/4 & sqrt/4 & 1/2 & sqrt/6 & -sqrt/12 & 1/2 & -sqrt/6 & -sqrt/12 \ sqrt/4 & -sqrt/4 & 0 & sqrt/3 & sqrt/12 & 0 & 0 & sqrt/4 \ sqrt/4 & sqrt/4 & 0 & 0 & sqrt/4 & 0 & sqrt/3 & -sqrt/12 end right) , . $$ $$ P^AP= left( begin 3&&&&&&& \ &-3&&&&&& \ &&1&&&&& \ &&&1&&&& \ &&&&1&&& \ &&&&&-1&& \ &&&&&&-1& \ &&&&&&&-1 end right) , . $$ ♦

Видео:Собственные значения и собственные векторыСкачать

Квадратичная форма

Экстремальное свойство собственных чисел

Пусть уравнение $ X^<^>A X=1 $ задает эллипсоид в $ mathbb R^3 $, т.е. квадратичная форма положительно определена. Построить посылочный ящик минимального объема (минимальный параллелепипед), содержащий данный эллипсоид.

Решение. Если уравнение эллипсоида приведено к каноническому виду $$ frac+frac+frac=1, $$ то ответ геометрически очевиден: эллипсоид «шире всего» в направлении оси, соответствующей максимальному из трех чисел $ a,b,c $, и «уже всего» в направлении оси, соответствующей минимальному из этих чисел. То есть размер оптимального посылочного ящика — $ (2,a, 2,b, 2,c) $. В случае, если уравнение $ X^<^>A X=1 $ не приведено к каноническому виду, его можно привести к нему с помощью ортогональной замены переменных. Такая замена оставляет инвариантными размеры эллипсоида, а результатом ее становится уравнение эллипсоида в каноническом виде $$ lambda_1 y_1^2+lambda_2 y_2^2+lambda_3 y_3^2=1 , . $$ Здесь $ lambda_1,lambda_2,lambda_3 $ — собственные числа матрицы $ A $, они являются положительными ввиду предположения о положительной определенности этой матрицы. Соответствующие собственные векторы матрицы определяют главные оси эллипсоида 1) . Сравнивая два канонических вида уравнения эллипсоида, можем размеры посылочного ящика сформулировать в терминах собственных чисел матрицы: максимальный размер эллипсоид имеет равным $ 2/sqrt<min > $, а минимальный — равным $ 2/sqrt<max > $. Если эллипсоид нельзя поворачивать вокруг начала координат, то для того, чтобы поместить его в ящик размеров $ 2/sqrt, 2/sqrt, 2/sqrt $ последний надо ориентировать в пространстве: рёбра должны быть параллельны собственным векторам матрицы $ A $. ♦

Замеченное свойство собственных чисел симметричной матрицы распространяется и в многомерное пространство. Традиционно его формулируют в несколько ином виде — хотя и менее наглядном, но более ориентированном на приложения в задачах механики и статистики.

Задача. Найти условные экстремумы квадратичной формы $ F(X)=X^<^>A X $ на единичной сфере $$ mathbb S= , . $$

В курсе математического анализа показывается, что, во-первых, указанные экстремумы существуют 2) , и, во-вторых, могут быть найдены применением метода множителей Лагранжа.

Теорема. Если $ lambda_ $ — максимальное, а $ lambda_ $ — минимальное собственные числа матрицы $ A $, то

$$ max_ X^<^>A X =lambda_, qquad min_ X^<^>A X =lambda_ , . $$ Указанные экстремумы квадратичная форма достигает на соответствующих собственных векторах матрицы $ A $ единичной длины.

Доказательство. Применяем метод множителей Лагранжа, т.е. составляем функцию $$L(X,lambda) = F(X)- lambda (X^X-1)$$ и ищем ее абсолютные экстремумы (как функции $ (n+1) $-го аргумента). На основании теоремы о стационарных точках полинома эти экстремумы должны достигаться на вещественных решениях системы уравнений $$ left< begin big/=&2left(a_x_1+a_x_2+dots+a_x_n right)-2 lambda x_1 &=0, \ dots & & dots \ big/=&2left(a_x_1+a_x_2+dots+a_x_n right)-2 lambda x_n &=0, \ big/=&x_1^2+dots +x_n^2-1 &= 0 , . end right. $$ Решаем эту систему. Первые $ n $ уравнений перепишем в матричном виде $$AX-lambda X=mathbb O iff (A-lambda , E) X=mathbb O , . $$ Из последнего уравнения системы следует, что $ X ne mathbb O $. Следовательно, решениями системы будут исключительно только собственные векторы $ _j $ матрицы $ A $, при $ lambda $ равном соответствующему собственному числу $ lambda_j $ этой матрицы. При $ X=_j $ и $ lambda=lambda_j $ получаем экстремальные значения функции $ F(X) $: $$F(_j)=_j^<^>A _j = lambda_j _j^<^>_j=lambda_j , . $$ Откуда и следует утверждение теоремы. ♦

Еще один вариант экстремального свойства симметричной матрицы излагается ☞ ЗДЕСЬ.

Видео:А.7.35 Собственные вектора и собственные значения матрицыСкачать

Собственные числа и собственные векторы матрицы

Определение 9.3. Вектор х называется собственным вектором матрицы А, если найдется такое число λ, что выполняется равенство: Ах= λх, то есть результатом применения к х линейного преобразования, задаваемого матрицей А, является умножение этого вектора на число λ. Само число λ называетсясобственным числом матрицы А.

Подставив в формулы (9.3) x`_j = λx_j, получим систему уравнений для определения координат собственного вектора:

.

. (9.5)

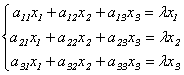
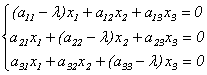
Эта линейная однородная система будет иметь нетривиальное решение только в случае, если ее главный определитель равен 0 (правило Крамера). Записав это условие в виде:

получим уравнение для определения собственных чисел λ, называемое характеристическим уравнением. Кратко его можно представить так:

поскольку в его левой части стоит определитель матрицы А-λЕ. Многочлен относительно λ | A — λE| называется характеристическим многочленом матрицы А.

Свойства характеристического многочлена:

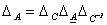
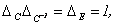
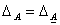
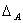
1) Характеристический многочлен линейного преобразования не зависит от выбора базиса. Доказательство. (см. (9.4)), но следовательно, . Таким образом, не зависит от выбора базиса. Значит, и |A-λE| не изменяется при переходе к новому базису.

2) Если матрица А линейного преобразования является симметрической (т.е. а_ij=a_ji), то все корни характеристического уравнения (9.6) – действительные числа.

Свойства собственных чисел и собственных векторов:

1) Если выбрать базис из собственных векторов х₁, х₂, х₃, соответствующих собственным значениям λ₁, λ₂, λ₃ матрицы А, то в этом базисе линейное преобразование А имеет матрицу диагонального вида:

(9.7) Доказательство этого свойства следует из определения собственных векторов.

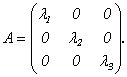
2) Если собственные значения преобразования А различны, то соответствующие им собственные векторы линейно независимы.

3) Если характеристический многочлен матрицы А имеет три различных корня, то в некотором базисе матрица А имеет диагональный вид.

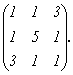
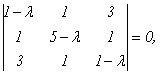
Найдем собственные числа и собственные векторы матрицы Составим характеристическое уравнение: (1- λ)(5 — λ)(1 — λ) + 6 — 9(5 — λ) — (1 — λ) — (1 — λ) = 0, λ³ — 7λ² + 36 = 0, λ₁ = -2, λ₂ = 3, λ₃ = 6.

Найдем координаты собственных векторов, соответствующих каждому найденному значению λ. Из (9.5) следует, что если х₍₁₎=<x₁,x₂,x₃> – собственный вектор, соответствующий λ₁=-2, то

— совместная, но неопределенная система. Ее решение можно записать в виде х₍₁₎=<a,0,-a>, где а – любое число. В частности, если потребовать, чтобы |x₍₁₎|=1, х₍₁₎=

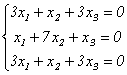
Подставив в систему (9.5) λ₂=3, получим систему для определения координат второго собственного вектора — x₍₂₎=<y₁,y₂,y₃>:

, откуда х₍₂₎=<b,-b,b> или, при условии |x₍₂₎|=1, x₍₂₎=

, x₍₃₎=<c,2c,c> или в нормированном варианте

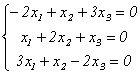
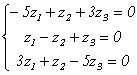
х₍₃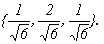₎ = Можно заметить, что х₍₁₎х₍₂₎ = ab – ab = 0, x₍₁₎x₍₃₎ = ac – ac = 0, x₍₂₎x₍₃₎ = bc — 2bc + bc = 0. Таким образом, собственные векторы этой матрицы попарно ортогональны.

Лекция 10.

Квадратичные формы и их связь с симметричными матрицами. Свойства собственных векторов и собственных чисел симметричной матрицы. Приведение квадратичной формы к каноническому виду.

Определение 10.1. Квадратичной формой действительных переменных х₁, х₂,…,х_n называется многочлен второй степени относительно этих переменных, не содержащий свободного члена и членов первой степени.

Примеры квадратичных форм:

(n = 2),

(n = 3). (10.1)

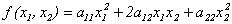
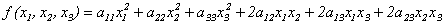
Напомним данное в прошлой лекции определение симметрической матрицы:

Определение 10.2. Квадратная матрица называется симметрической, если 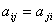, то есть если равны элементы матрицы, симметричные относительно главной диагонали.

Свойства собственных чисел и собственных векторов симметрической матрицы:

1) Все собственные числа симметрической матрицы действительные.

Доказательство (для n = 2).

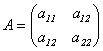
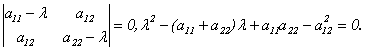
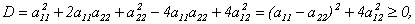
Пусть матрица А имеет вид: . Составим характеристическое уравнение:

(10.2) Найдем дискриминант:

следовательно, уравнение имеет только действительные корни.

2) Собственные векторы симметрической матрицы ортогональны.

Доказательство (для n = 2).

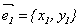
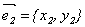
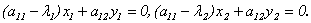
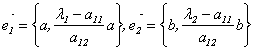
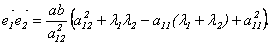
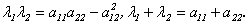
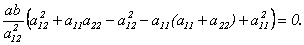
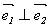
Координаты собственных векторов и должны удовлетворять уравнениям:

Следовательно, их можно задать так:

. Скалярное произведение этих векторов имеет вид:

По теореме Виета из уравнения (10.2) получим, что Подставим эти соотношения в предыдущее равенство: Значит, .

Замечание. В примере, рассмотренном в лекции 9, были найдены собственные векторы симметрической матрицы и обращено внимание на то, что они оказались попарно ортогональными.

Определение 10.3. Матрицей квадратичной формы(10.1) называется симметрическая матрица 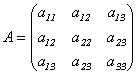. (10.3)

Таким образом, все собственные числа матрицы квадратичной формы действительны, а все собственные векторы ортогональны. Если все собственные числа различны, то из трех нормированных собственных векторов матрицы (10.3) можно построить базис в трехмерном пространстве. В этом базисе квадратичная форма будет иметь особый вид, не содержащий произведений переменных.

Видео:Собственные значения и собственные векторы. ПримерСкачать

Игра в собственные

Имеем набор данных в виде совокупности квадратных матриц, которые используются — вместе с известным выходом — в качестве тренировочного набора для нейронной сети. Можно ли обучить нейронную сеть, используя только собственные значения матриц? Во избежание проблем с комплексными значениями, упор делаем на симметричные матрицы. Для иллюстрации используем набор данных MNIST. Понятно, что невозможно восстановить матрицу по ее собственными значениям — для этого понадобится еще кое-что, о чем мы поговорим далее. Поэтому трудно ожидать некоего прорыва на данном пути, хотя известно, что можно говорить о чем угодно, строить грандиозные планы, пока не пришло время платить. О деньгах мы здесь не говорим, просто задаем глупый вопрос, на который постараемся получить осмысленный ответ, тем более что в процессе познания расширим свои научные горизонты. Например, сначала мы познакомимся с тем, как находить собственные векторы и собственные значения (eigenvalues and eigenvectors) для заданной квадратной матрицы, затем плавно выкатим на эрмитовы и унитарные матрицы. Все иллюстративные примеры сопровождаются простыми кодами. Далее возьмем MNIST , преобразуем в набор собственных значений симметричных матриц и используем молоток от Keras. Как говорят в Японии: “Торчащий гвоздь забивают”. Закроем глаза и начнем бить, а на результат можно и не смотреть: получится как всегда. Сразу скажу, что изложение будет проведено как можно ближе к тому, как я это дело понимаю для себя, не обращаясь к строгому обоснованию, которое обычно не используется в повседневной жизни. Иными словами, что понятно одному глупцу, понятно и другому. Все мы невежественны, но, к счастью, не в одинаковой степени. С другой стороны, предполагаю, что многие, хоть и в гимназиях не обучались, но имеют представление — по своему опыту обучения, — что значит впихнуть невпихуемое.

Собственно, собственные

Итак, пусть у нас задана произвольная квадратная матрица с компонентами . Мы ставим запятую между индексами, имея в виду оформление массивов в большинстве языков программирования; обычно так не делается, но мы делаем так, как нам хочется, да и выглядит все более разреженным и удобочитаемым. Мы можем умножить матрицу на произвольный вектор , руководствуясь правилом умножения матриц (строка на столбец), . По повторяющимся индексам производится суммирование; все получится, если размерность первой (нумерация с нуля) оси матрицы совпадает с размерностью вектора. Если будет желание, когда я что-то упускаю из виду, можно заглянуть в мои заметки . Вдруг приключилось так, что , тогда говорят: — собственное значение, — собственный вектор. Опять же, возвращаясь к глубокомысленной дискуссии о запятых в индексах, здесь мы используем точку, когда переходим от компонент к матрицам, имея в виду замечательную функцию dot() в превосходном NumPy. Теперь проведем ряд очевидных манипуляций

где — символ Кронекера, — единичная матрица, 0 — нулевой вектор. Условие нетривиальности решения, , для собственного вектора приводит к характеристическому уравнению . Если размер матрицы равен n, получим алгебраическое уравнение n-й степени, которое имеет n корней (действительных или комплексных) — собственных значений (eigenvalues) . Каждому собственному значению соответствует собственный вектор (eigenvectors) (например, ). Совокупность собственных векторов образует матрицу с компонентами , где нулевая ось — компоненты вектора, а первая — нумерация собственных векторов. Теперь уравнение на собственные значения выглядит следующим образом: . Раз есть вектор, есть его длина, которая равна сумме квадратов компонент (квадрат длины). Например, для квадрата длины третьего вектора (нумерация с нуля) имеем

где, вспоминая правила умножения матриц ( , см. заметки ), мы воспользовались тождеством , в котором — транспонированная матрица (используем обозначения NumPy). Здесь нет проблем, но это до тех пор, пока мы работаем с действительными векторами. В комплексной области квадрат длины вектора равен скалярному произведению вектора на комплексно сопряженный. В этом случае потребуется следующая модификация соотношения (2):

где звездочка обозначает обычное комплексное сопряжение. Следует заметить, что — эрмитово-сопряжённая матрица. Длина вектора — число, отсюда открывается возможность выделить собственное значение путем умножения на собственный вектор. В результате для выделенного собственного значения получим

Все это выглядит не очень хорошо, поскольку произведение разных собственных векторов, например , может быть не равно нулю. Это настораживает, поскольку мы привыкли иметь дело с единичными векторами, каждый из которых ортогонален другому. Вспомните хотя бы единичные векторы по трем осям в обычном пространстве. Но проблемы отложим на потом, а пока создадим видимость работы — побалуемся с кодами.

Действительно, характеристическое уравнение имеет решения , где — мнимая единица. Столбцы матрицы — собственные векторы и .

Эрмитовы матрицы

Мы научились находить eigendecomposition для произвольной квадратной матрицы. Пока не будем говорить о вырожденных матрицах , которых, по возможности, будем в дальнейшем избегать. Итак, в чем состоит загвоздка. С собственными значениями — все в порядке, а вот собственные векторы изрядно подгуляли. Дело в том, что они не ортогональны друг другу. Посмотрим, какие условия на матрицу нам потребуется наложить, чтобы добиться ортогональности, заодно откроем для себя ряд новых возможностей в деле познания собственных способностей.

Пусть из всего набора мы произвольно выделили два участника и , где, напомним, второй индекс нумерует собственные вектора. Берем первое соотношение и умножаем его на , а второе — на , в результате имеем

Далее выполним комплексное сопряжение второго уравнения в (5)

Поскольку индексы в последнем уравнении “немые” (по ним производится суммирование) , их можно назвать как угодно. Таким образом, после замены получим

где — эрмитово-сопряжённая матрица, элементы которой определяются как . Теперь из первого уравнения (5) вычитаем (6). В результате получим следующее замечательное выражение:

Пока мы не накладывали никаких ограничений на матрицу. Первое, что приходит на ум: положим , определяя тем самым эрмитову матрицу Следует отметить: все что мы наблюдаем в окружающем нас мире связано, так или иначе, с собственными значениями эрмитовых матриц. Шарль Эрмит — вот кто Создатель Вселенных (см. превосходную биографию, Ожигова Е.П. Шарль Эрмит. — Л.:Наука, 1982.). Да, было время, когда математики занимались реальным миром, не то, что нынешнее племя.

Шарль Эрмит, 1822-1901

Итак, для эрмитовых матриц получаем выражение , которое связано с двумя важнейшими событиями для каждого, кто изучал квантовую механику. Во-первых, собственные значения эрмитовых матриц являются действительными величинами , поскольку при из условия 0″ alt=»v_^*v_>0″ src=»https://habrastorage.org/getpro/habr/upload_files/d8c/47c/bbb/d8c47cbbbf641fa3ff4843e155e4fd7c.svg»/>имеем . Во- вторых, если и , получаем свойство ортогональности собственных векторов . Для эрмитовых матриц собственные значения — действительные величины, а собственные векторы — ортогональны друг другу, вернее, ортонормированы, поскольку удобно включать условие нормировки. Таким образом, мы стремились к аналогии с обычным пространством, с единичными векторами по ортогональным осям, мы это и получили.

Теперь соорудим эрмитову матрицу. Для этого сгенерируем пару случайных матриц и , затем сложим их, умножив одну из матриц на мнимую единицу , . Затем возьмем полученную матрицу и сложим ее с эрмитово-сопряженной. Действительно, , так что — эрмитова матрица.

Пришло время окунуться в мутные воды искусственного интеллекта. Внести, так сказать, свой слабый голос в общий хор.

Собственные значения (values) получились с едва заметной мнимой частью, которую мы отрезаем по идеологическим соображениям. Для этого мы оставили только действительную часть. Напомним, что

где — единичная матрица (по диагонали единицы ). Проверим в коде

Опять же получим почти единичную матрицу, но ничего округлять не будем. Теперь пришло время для громкого заявления : матрица, для которой выполняется (8) — унитарная матрица . Таким образом, эрмитово-сопряжённая унитарная матрица совпадает с обратной. К слову, эволюция во времени нашего мира осуществляется с помощью унитарных преобразований, хотя этот факт теряется во множестве событий. Не удивительно, что унитарную эволюцию попытались использовать (см. статью) и в машинном обучении, но для рекуррентной нейронной сети. Для многих концепция унитарности заставляет ощутить священный трепет познания. Но это одна среда обитания. В политическом же питательном бульоне тоже есть концепция унитарности, о которой можно думать все что угодно, и которая не связана ни с каким познанием.

Симметричный MNIST

Итак, в предыдущем разделе мы говорили о произвольных о эрмитовых матрицах. Если же мы имеем дело с действительными матрицами, комплексное сопряжение выпадает, поэтому эрмитовы — это просто симметричные матрицы, ​​.

В этом разделе мы возьмем набор данных MNIST и попробуем поработать с каждым элементом как с матрицей. Каждое рукописное изображение цифр (от 0 до 9) — матрица с формой (28,28), каждый элемент которой — число от 0 до 255 (8-битная шкала серого). Загрузим и посмотрим (рекомендую начать новый блокнот).

База данных MNIST состоит тренировочного и тестового наборов, где — набор рукописных изображений цифр(матриц), которые подаем на вход, а — набор правильных ответов (числа от 0 до 9); тестовый набор выделен для удобства. Теперь посмотрим, сколько их там, и что они из себя представляют. Для этого подключим “рисовалку”.

Все выглядит замечательно, так что можно продолжать работать с нашим изображением. Тем не менее, проблемы вылазят тогда, когда мы посмотрим на матрицу, скрывающуюся под этим изображением.

Сразу можно отметить (посмотрите сами), что слишком много нулей. Это вырожденная матрица, определитель ее равен нулю.

Если попробуем вычислить собственные значения, никакого сбоя не случится, просто некоторые из них будут равны нулю.

Как видно, собственные значения находятся в комплексной области. Монтировать комплексную нейронную сеть можно, но осторожно. Основы и ссылки можно подчерпнуть из диссертации. Это отличная тема для исследований и экспериментов; советую использовать только аналитические функции, несмотря на ограничения, связанные с принципом максимума модуля (это для тех, кто в теме).

Итак, хочется поскорее избавиться от комплексных чисел. Мы знаем, что эрмитовы матрицы обладают действительными собственными значениями. Поскольку матрица изображения полностью состоит из действительных чисел, то эрмитова матрица — просто симметричная матрица. Иными словами, нам потребуется соорудить симметричную матрицу, но перед этим избавиться от множества нулей. Для этого “закрасим” пикселями, выбирая их значения случайным образом.

Пятерочки для закраски вполне достаточно, поскольку вероятность совпадения элементов в строке или столбце просто мизерная. Детерминант, конечно, громадный, но Python все стерпит, а пока закроем на это глаза. Если посмотрим на картинку, то поверьте, там все нормально: наша тройка практически не изменилась.

Итак, перейдем к симметричной матрице и посмотрим, что там нарисовано.

Кто скажет, что это не тройка, пусть первый бросит в меня камень! Теперь это число подготовлено для манипуляций в нейронной сети. Матрица симметричная, невырожденная, имеет замечательный набор собственных значений.

Если с собственными значениями все в порядке, то собственные векторы малость подгуляли: мало того, что они комплексные (как обычно и бывает), так восстановление первоначальной матрицы по собственным векторам и собственным значениям может привести к комплексной матрице. Python не знает, что это не правильно, поэтому и вытянет наружу комплексные остатки. Само собой, можно от них избавиться с помощью метода np.real(), оставляя только действительную часть. Но пока попробуем в лоб, проверим прозорливость создателей NumPy на примере восстановления матрицы по собственным значениям и собственным векторам. Чтобы подготовить почву, необходимо вернуться к уравнениям (8), которые справедливы и для нашей матрицы , в которой столбцы — собственные векторы матрицы (см. выше). Таким образом, . Следует напомнить, что, несмотря на повторяющийся индекс ​​, в правой части нет суммирования (берем фиксированное ​​). Далее имеем

где — диагональная матрица собственных значений (по диагонали — собственные значения). Умножая последнее уравнение с правой стороны на , получим

в котором использовали (8) . Теперь проверим в коде

Нет слов, все работает! Итак, наши подозрения были беспочвенны, но проверять все равно надо. Теперь мы знаем, что по собственным значениям и векторам можно четко восстановить исходную матрицу. Итак, если используем обратимые операции, царапая формулы на листке бумаге, лучше проверить, как с этим обстоит дело в коде.

Эксперимент

Итак, теперь мы умеем манипулировать симметричными матрицами, используя в качестве полигона базу данных MNIST. Теперь мы попытаемся представить набор данных как симметричные матрицы, затем вычислить собственные значения, на основе которых построить нейронную сеть по примеру обращения с обычным набором. Сразу скажу, что надежд на удачный исход мало. Действительно, как мы выяснили ранее, для того чтобы восстановить матрицу собственных значений недостаточно, для этого необходим набор собственных векторов, объединенных в матрицу , которая сама по себе имеет размер исходной матрицы. Так что, с первого взгляда, мы ничего не выигрываем. Тем не менее, есть надежда, что распределение и свойства собственных значений обладают необходимыми свойствами, чтобы их классифицировать по классам. Иными словами, собственные значения несут информацию о классах рукописных цифр. Распределением собственных значений мы займемся в следующей публикации, а сейчас будем использовать наивный подход, а именно : 1) представим набор MNIST в виде симметричных матриц (28*28); 2) для каждого экземпляра вычислим собственные значения (28 штук); 3) используем Keras. Первые шаги мы уже сделали в предыдущем разделе, а над последним особо заморачиваться не будем, поскольку мы просто ставим эксперименты.

Начинаем новый блокнот:

Теперь напишем функцию, которая будет “закрашивать” матрицы из набора данных. Отмечу, что использую доморощенные функции, которые предпочитаю писать самостоятельно, чем искать на мутных форумах.

Используем эту функцию, затем масштабируем (это не обязательно).

На следующем шаге нам понадобится функция, которая делает симметричные матрицы и возвращает только собственные значения.

Включаем и смотрим.

Как видно, вполне приемлемые значения, с которыми можно и поработать. Для этого возьмем продвинутый молоток от Keras.

За основу мы берем код из Глубокое обучение на Python. Если осмысленно побалуетесь с цифрами, что-то получите. Точность, которая едва-едва заваливает за 0,5 (за 100 эпох. ), подкачала по сравнению с оригиналом (accuracy: 0.9897 за Epoch 5), когда используется полная матрица изображения, но хотя бы мы не множили сущности. Для обсуждения не требуется глубокомысленных обобщений, просто, как я наивно думал, если зайца долго бить по голове, он научится спички зажигать. Но оказалось, что этот принцип в глубоком обучении не всегда срабатывает. Возиться дальше — интересно, но бессмысленно. Самое главное, по пути к этому мутному результату можно много чему научиться.

Пару слов напоследок

Итак, пришло время подводить итоги. Понятно, что говорить пока не о чем. Мы попытались на собственных значениях матриц построить работающую схему. Не получилось. Но известно, что отрицательный результат — куда более значимое событие, чем положительный, поскольку при этом у нас открываются новые перспективы. Если бы у нас все получилось, настало бы время для рутинной работы, а так — продолжим идти дальше. Правда и ложь — два взгляда на одну и ту же реальность. Но мы, по крайней мере, не лгали. Просто посмотрели с другого ракурса, заодно открыли для себя новые возможности. К примеру, почему бы не найти преобразование, позволяющее связать все изображения одного класса без использования внешнего наблюдателя для подтверждения события? Иными словами, из одной цифры получить почти полную совокупность из данного набора данных; из “тройки” почти все “тройки”, и т.д.. Сразу приходит на ум конформное отображение двумерных поверхностей: локальные вращения и растяжения с сохранением углов между кривыми, а значит с сохранением формы бесконечно малых фигур. Заодно мы могли бы проследить за трансформацией собственных значений, дабы по их расположению выйти на классификацию по классам. И не обязательно использовать действительные собственные значения. Конечно, переход в комплексную область потребует дополнительных усилий, но там уже существует путь в один путь, многое успешно отработано.

Что касается реальных, на настоящий момент, дел, то это классификация собственных значений по примеру распределения уровней сложных систем. Опять же MNIST животворящий. Но это тема следующей публикации.

📹 Видео

Собственные значения и собственные векторы. ТемаСкачать

Айгенвектора и айгензначения | Сущность Линейной Алгебры, глава 10Скачать

7 4 Собственные векторы и собственные значенияСкачать

Овчинников А. В. - Линейная алгебра - Собственные значения и собственные векторы линейного оператораСкачать

Матрицы и векторыСкачать

Собственные векторы и собственные значенияСкачать

Квантовая механика 8 - Операторы. Собственные векторы и собственные значения.Скачать

Сингулярное удовольSVDиеСкачать

Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Собственные значения матрицыСкачать

Собственные числа, собственные, присоединенные векторы. Матрица оператора в базисе...Скачать