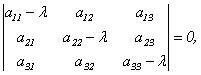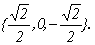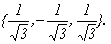Собственные векторы матрицы ортогональны (3 видео)

Ортогональность собственных векторов.

Теорема: собственные векторы симметричного линейного оператора, соответствующие различным собственным числам, взаимно ортогональны.

Пусть векторы и — собственные векторы оператора соответствующие собственным числам λ₁ и λ₂, причем λ₁≠λ₂ . По определению симметричного оператора:

. Подставляя сюда и получим . Вынесем λ₁ и λ₂ за знак скалярного произведения, перенесем все влево и разложим на множители и получим , так как λ₁≠λ₂ , то =0, что означает взаимную ортогональность векторов и .

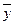
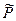
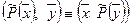
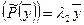
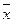
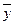
Квадратичные формы.

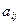
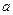
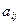
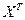
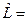
Пусть L=( )- симметричная матрица n-го порядка, тогда выражение -называется квадратичной формой переменных x₁,x₂. x_n. Матрица L=( _ij) i,j=(1,2. n) -называется матрицей квадратичной формы. Пусть( ) –симметричная матрица, т.е. = . В матричной форме квадратичная форма имеет вид :

, где X= -матрица столбец переменных, а = — матрица строка этих же переменных. Найдем произведение этих матриц.

-что является по определению квадратичной формой.

Канонический вид квадратичной формы

Следует отметить, что с помощью некоторых линейных преобразований квадратичную форму можно привести к наиболее простому каноническому виду. Квадратичная форма называется канонической, если все ее коэффициенты при i ≠ j ,т.е.

матрица канонической квадратичной формы является диагональной.

Теорема. Любая квадратичная форма с помощью линейных преобразований может быть приведена к каноническому виду.

Канонический вид квадратичной формы не является однозначно определенным, так как одна и та же квадратичная форма может быть приведена к каноническому виду многими способами. Однако полученные различными способами канонические формы обладают рядом общих свойств. Одно из них — закон инерции квадратичных форм формулируется в виде теоремы.

Теорема (закон инерции квадратичных форм). Число слагаемых с положительными (отрицательными) коэффициентами квадратичной формы не зависит от способа приведения формы к этому виду.

IV Аналитическая геометрия на плоскости.

Система координат. Основные понятия.

Под системой координат на плоскости понимают способ, позволяющий численно описать положение точки плоскости. Одной из таких систем является прямоугольная (декартова) система координат. Она задается двумя взаимно перпендикулярными прямыми — осями, на каждой из которых выбрано направление и задан масштабный единичный отрезок. Единицу масштаба обычно берут одинаковую для обеих осей. Эти оси называются осями координат, а точка их пересечения – О- началом координат. Одна ось- ось абсцисс (Оx), вторая- ординат (Оy).

На рисунках ось абсцисс, как правило, располагается горизонтально и слева направо, ось ординат вертикально и снизу вверх. Единичные векторы осей обозначают i и j (|i|=|j|=1,i перпенд. j ).

Рассмотрим произвольную точку М на плоскости Оxy. Вектор называется радиусом вектора. Координатами точки М называются координаты радиуса вектора ОМ. Если ОМ= (x ,y), то координаты т.М(x,y). Другой важной системой координат является полярная система координат.

Полярная система координат задается точкой О называемой полюсом, лучом Оp называемом полярной осью и единичным вектором 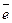того же направления, что и луч Оp.

Возьмем точку М не совпадающую с О. Положение т.М определяется двумя числами ее расстоянием rот полюса О и углом образованным отрезком ОМ с полярной осью (отсчет углов ведется в направлении противоположном движению часовой стрелки. Числа r и φ называются полярными координатами т.М (r, ), r – полярный радиус, — полярный угол.

Установим связь между декартовыми и полярными координатами. Для этого совместим полюс с системой координат Оxy, а полярную ось с + полуосью Ox. Тогда т.М в прямоугольной системе М( x,y),а в полярном M(r,φ).тогда из рисунка 1

y M(x,y)

или y

Рис.1

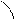
O Xx

1) Линия на плоскости(основные понятия)

Уравнение линии(кривой) на плоскости Oxy называют такое уравнение F(x,y)=0 с двумя переменными, которому удовлетворяют координаты x и y каждой точки линии и не удовлетворяют координаты любой точки не лежащей на этой линии. Если точка M(x,y) передвигается по линии, то ее координаты изменяясь, удовлетворяют уравнению этой линии.

Пример: лежат ли точки А(-2,1) и В(1,1) на линии 2x+y+3=0.

Решение. Подставляя в уравнение вместо x и y координаты точек А и В получим в первом тождество во втором нет. Следовательно т. А лежит на линии, т.В- нет.

Уравнение линии на плоскости можно задать при помощи двух уравнений:

Где x и y- координаты т.М(x,y),лежащей на данной линии, а t-переменная называемая параметром. Параметр t определяет положение точки (x,y) на плоскости. Если параметр t меняется, то точка на плоскости перемещается, описывая данную линию. Такое уравнение называется параметрическим уравнением линии. Для перехода от параметрического вида к обычному достаточно из уравнений (1) исключить t. Каким-либо образом линию на плоскости можно задать векторным уравнением , где t – скалярный переменный параметр. Каждому t₀ соответствует определенный вектор r₀=r(t₀). При изменении параметра t конец вектора r=r(t) опишет заданную линию.

Векторное уравнение и параметрическое уравнение имеют механический смысл. Если точка перемещается на плоскости, то указанные уравнения называются уравнениями движения, а линия- траекторией движения, параметр t при этом– время.

В аналитической геометрии на плоскости, вообще говоря, возникают две задачи:

1) зная геометрические свойства кривой, найти ее уравнение

2)зная уравнение кривой изучить ее форму и свойства.

Содержание

Собственные числа и собственные векторы матрицы
VMath
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Симметричная матрица
Определитель
Миноры: тождества Кронекера
Произведение
Обратная матрица
Характеристический полином, собственные числа, собственные векторы
Локализация собственных чисел
Диагонализуемость
Квадратичная форма
Экстремальное свойство собственных чисел
🔍 Видео

Видео:Собственные векторы и собственные числа линейного оператораСкачать

Собственные числа и собственные векторы матрицы

Определение 9.3. Вектор х называется собственным вектором матрицы А, если найдется такое число λ, что выполняется равенство: Ах= λх, то есть результатом применения к х линейного преобразования, задаваемого матрицей А, является умножение этого вектора на число λ. Само число λ называетсясобственным числом матрицы А.

Подставив в формулы (9.3) x`_j = λx_j, получим систему уравнений для определения координат собственного вектора:

. (9.5)

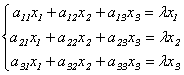
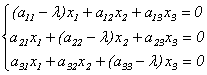
Эта линейная однородная система будет иметь нетривиальное решение только в случае, если ее главный определитель равен 0 (правило Крамера). Записав это условие в виде:

получим уравнение для определения собственных чисел λ, называемое характеристическим уравнением. Кратко его можно представить так:

поскольку в его левой части стоит определитель матрицы А-λЕ. Многочлен относительно λ | A — λE| называется характеристическим многочленом матрицы А.

Свойства характеристического многочлена:

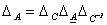
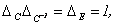
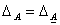
1) Характеристический многочлен линейного преобразования не зависит от выбора базиса. Доказательство. (см. (9.4)), но следовательно, . Таким образом, не зависит от выбора базиса. Значит, и |A-λE| не изменяется при переходе к новому базису.

2) Если матрица А линейного преобразования является симметрической (т.е. а_ij=a_ji), то все корни характеристического уравнения (9.6) – действительные числа.

Свойства собственных чисел и собственных векторов:

1) Если выбрать базис из собственных векторов х₁, х₂, х₃, соответствующих собственным значениям λ₁, λ₂, λ₃ матрицы А, то в этом базисе линейное преобразование А имеет матрицу диагонального вида:

(9.7) Доказательство этого свойства следует из определения собственных векторов.

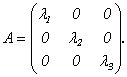
2) Если собственные значения преобразования А различны, то соответствующие им собственные векторы линейно независимы.

3) Если характеристический многочлен матрицы А имеет три различных корня, то в некотором базисе матрица А имеет диагональный вид.

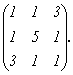
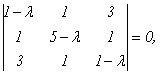
Найдем собственные числа и собственные векторы матрицы Составим характеристическое уравнение: (1- λ)(5 — λ)(1 — λ) + 6 — 9(5 — λ) — (1 — λ) — (1 — λ) = 0, λ³ — 7λ² + 36 = 0, λ₁ = -2, λ₂ = 3, λ₃ = 6.

Найдем координаты собственных векторов, соответствующих каждому найденному значению λ. Из (9.5) следует, что если х₍₁₎=<x₁,x₂,x₃> – собственный вектор, соответствующий λ₁=-2, то

— совместная, но неопределенная система. Ее решение можно записать в виде х₍₁₎=<a,0,-a>, где а – любое число. В частности, если потребовать, чтобы |x₍₁₎|=1, х₍₁₎=

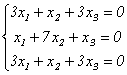
Подставив в систему (9.5) λ₂=3, получим систему для определения координат второго собственного вектора — x₍₂₎=<y₁,y₂,y₃>:

, откуда х₍₂₎=<b,-b,b> или, при условии |x₍₂₎|=1, x₍₂₎=

, x₍₃₎=<c,2c,c> или в нормированном варианте

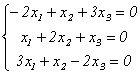
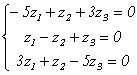
х₍₃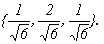₎ = Можно заметить, что х₍₁₎х₍₂₎ = ab – ab = 0, x₍₁₎x₍₃₎ = ac – ac = 0, x₍₂₎x₍₃₎ = bc — 2bc + bc = 0. Таким образом, собственные векторы этой матрицы попарно ортогональны.

Лекция 10.

Квадратичные формы и их связь с симметричными матрицами. Свойства собственных векторов и собственных чисел симметричной матрицы. Приведение квадратичной формы к каноническому виду.

Определение 10.1. Квадратичной формой действительных переменных х₁, х₂,…,х_n называется многочлен второй степени относительно этих переменных, не содержащий свободного члена и членов первой степени.

Примеры квадратичных форм:

(n = 2),

(n = 3). (10.1)

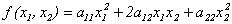
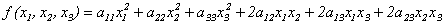
Напомним данное в прошлой лекции определение симметрической матрицы:

Определение 10.2. Квадратная матрица называется симметрической, если 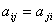, то есть если равны элементы матрицы, симметричные относительно главной диагонали.

Свойства собственных чисел и собственных векторов симметрической матрицы:

1) Все собственные числа симметрической матрицы действительные.

Доказательство (для n = 2).

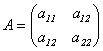
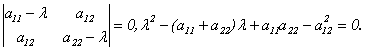
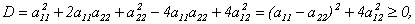
Пусть матрица А имеет вид: . Составим характеристическое уравнение:

(10.2) Найдем дискриминант:

следовательно, уравнение имеет только действительные корни.

2) Собственные векторы симметрической матрицы ортогональны.

Доказательство (для n = 2).

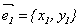
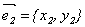
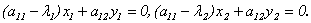
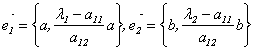
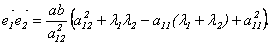
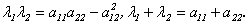
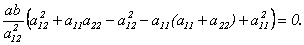
Координаты собственных векторов и должны удовлетворять уравнениям:

Следовательно, их можно задать так:

. Скалярное произведение этих векторов имеет вид:

По теореме Виета из уравнения (10.2) получим, что Подставим эти соотношения в предыдущее равенство: Значит, .

Замечание. В примере, рассмотренном в лекции 9, были найдены собственные векторы симметрической матрицы и обращено внимание на то, что они оказались попарно ортогональными.

Определение 10.3. Матрицей квадратичной формы(10.1) называется симметрическая матрица 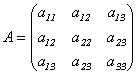. (10.3)

Таким образом, все собственные числа матрицы квадратичной формы действительны, а все собственные векторы ортогональны. Если все собственные числа различны, то из трех нормированных собственных векторов матрицы (10.3) можно построить базис в трехмерном пространстве. В этом базисе квадратичная форма будет иметь особый вид, не содержащий произведений переменных.

Видео:Собственные векторы и собственные значения матрицыСкачать

VMath

Инструменты сайта

Основное

Информация

Действия

Содержание

Страница — в разработке. Начало работ — 08.03.2014, окончание — .

Видео:Собственные значения и собственные векторы матрицы (4)Скачать

Симметричная матрица

Теорема. Для любой матрицы $ A_ $ матрицы $ A_A^ $ и $ A^ A $ — симметричны. Для любой квадратной матрицы $ A_ $ матрица $ A_+A^ $ — симметрична.

Видео:Диагональный вид матрицы. Приведение матрицы к диагональному виду. Собственные векторыСкачать

Определитель

Теорема [Кэли]. В полном разложении определителя симметричной матрицы порядка $ n $ обозначим $ mathfrak s_n $ число слагаемых, $ mathfrak s_n^ $ — число слагаемых с положительным знаком, $ mathfrak s_n^ $ — число слагаемых с отрицательным знаком, а $ mathfrak d_n =mathfrak s_n^ — mathfrak s_n^ $. Имеют место соотношения:

$$ mathfrak s_=(n+1)mathfrak s_n- C_n^2 mathfrak s_ ; $$ $$ mathfrak d_=-(n-1)mathfrak d_n- C_n^2 mathfrak d_ . $$

Имеют место пределы:

Миноры: тождества Кронекера

Теорема [Кронекер]. Для симметричной матрицы $ A_ $ порядка $ n ge k+1 $ имеет место тождество

$$ Aleft(begin 1 & 2 & dots & k-2 & k \ 2 & 3 & dots & k-1 & k+1 end right)- Aleft(begin 2 & 3 & dots & k-1 & k \ 1 & 2 & dots & k-2 & k+1 end right)= $$ $$ = Aleft(begin 1 & 2 & dots & k-3 & k-2 & k-1 \ 2 & 3 & dots & k-2 & k & k+1 end right) , $$ связывающее три ее минора порядка $ k-1 $.

Пример. Для $ k=4 $:

$$ Aleft(begin 1 & 2 & 4 \ 2 & 3 & 5 end right)- Aleft(begin 2 & 3 & 4 \ 1 & 2 & 5 end right)= Aleft(begin 1 & 2 & 3 \ 2 & 4 & 5 end right) $$ $$ iff left| begin a_ & a_ & a_ \ a_ & a_ & a_ \ a_ & a_ & a_ end right|- left| begin a_ & a_ & a_ \ a_ & a_ & a_ \ a_ & a_ & a_ end right|= left| begin a_ & a_ & a_ \ a_ & a_ & a_ \ a_ & a_ & a_ end right| . $$

В настоящем разделе минор матрицы $ A $ $$ Aleft( begin j_1 & dots & j_k \ j_1 & dots & j_k end right) = left|begin a_ & a_ & dots & a_ \ a_ & a_ & dots & a_ \ vdots & & ddots & vdots \ a_ & a_ & dots & a_ end right| , quad 1le j_1 ☞ ЗДЕСЬ.

Теорема. Если $ mathfrak r = operatorname (A)ge 1 $, то в матрице $ A $ существует ненулевой ведущий минор порядка $ mathfrak r $.

Видео:Собственные векторы и собственные числа линейного оператораСкачать

Произведение

Теорема. Для того, чтобы произведение симметричных матриц $ A $ и $ B $ было симметричной матрицей необходимо и достаточно, чтобы матрицы $ A $ и $ B $ коммутировали: $ AB = BA $.

Видео:Собственные значения и собственные векторыСкачать

Обратная матрица

Теорема. Обратная к симметричной матрице (если существует) будет симметричной матрицей.

Видео:А.7.35 Собственные вектора и собственные значения матрицыСкачать

Характеристический полином, собственные числа, собственные векторы

Теорема 1. Все собственные числа симметричной матрицы вещественны.

Доказательство ☞ ЗДЕСЬ.

Если $ lambda=0 $ корень кратности $ mathfrak m $ характеристического полинома симметричной матрицы $ A $, т.е.

$$ det (A-lambda E)equiv(-1)^n lambda^n+a_1lambda^+dots+a_ lambda^ quad npu a_ne 0 $$ то $ operatorname (A)=n-mathfrak m $.

Если в характеристическом полиноме некоторый коэффициент $ a_j $ при $ j notin $ обращается в нуль, то соседние с ним в нуль не обращаются и имеют различные знаки: $ a_ a_ ♦

Локализация собственных чисел

Теорема [Коши]. Для симметричной матрицы $ A_ $ число ее собственных чисел, лежащих на интервале $ ]a,b_[ $, определяется по формуле:

Согласно этой теореме, главные миноры матрицы $ A-lambda, E $ играют роль системы полиномов Штурма для характеристического полинома симметричной матрицы $ A_ $.

$$ A_1,A_2,dots,A_ $$ симметричной матрицы $ A_ $ отличны от нуля, то число положительных собственных чисел матрицы $ A_ $ равно числу знакопостоянств, а число отрицательных собственных чисел — числу знакоперемен в ряду $ 1,A_1,dots,A_n $:

Часто в приложениях требуется вычислить значения не всех собственных чисел симметричной матрицы, а только небольшого (по сравнению с порядком матрицы) количества максимальных по модулю. Численный метод решения этой задачи изложен ☞ ЗДЕСЬ.

Видео:2 42 Ортогональность векторовСкачать

Диагонализуемость

Теорема. Существует ортогональная матрица $ P_ $, приводящая симметричную матрицу $ A_ $ к диагональному виду:

$$ P^AP=P^<^>AP= left( begin lambda_1 & & & mathbb O \ & lambda_2 & & \ && ddots & \ mathbb O&& & lambda_n end right). $$

Доказательство особенно просто в случае когда все собственные числа $ lambda_1,dots, lambda_n $ различны. На основании теоремы 1 матрица $ A_ $ диагонализуема над множеством вещественных чисел и на основании теоремы 2 матрица $ P $, приводящая к диагональному виду, может быть выбрана ортогональной.

Для общего случая доказательство производится индукцией по порядку $ n $ матрицы $ A $. Окончание доказательства ☞ ЗДЕСЬ. ♦

Теорема утверждает что даже при наличии кратных корней у характеристического полинома $$ f(lambda)=(-1)^n(lambda — lambda_1)^<_1> times dots times (lambda — lambda_)^<_>, quad _1+dots+_<>=n, lambda_k ne lambda_ npu k ne ell $$ алгебраическая кратность собственного числа $ lambda_j $ совпадает с его геометрической кратностью: $$operatorname , (A-lambda_j, E)= _j, npu quad forall jin .$$ Или, что то же: размерность собственного подпространства $$ left <Xin mathbb R^n , big| , (A-lambda_j, E)X=mathbb O_right> $$ равна $ _j $. При нахождении фундаментальной системы решений (ФСР) указанной системы уравнений мы получим $ _j $ линейно независимых собственных векторов $ <_,dots, _<j_j> > $ , принадлежащих $ lambda_j $. Однако при традиционных способах построения ФСР вовсе не гарантирована ортогональность этих векторов. Как построить ФСР так, чтобы она удовлетворяла условию теоремы, т.е. была ортонормированной? Воспользуемся для этого процессом ортогонализации Грама-Шмидта, применив его к системе $ <_,dots, _<j_j> > $. Результатом процесса будет новая система векторов $ <_,dots, _<j _j> > $ такая что ее линейная оболочка совпадает с линейной оболочкой исходной системы: $$ left(_,dots, _<j _j> right)= left(_,dots, _<j_j> right) quad mbox quad langle _,_ rangle =0 mbox k ne ell , , $$ т.е. векторы $ _,dots, _<j _j> $ остаются собственными векторами, принадлежащими $ lambda_j $. Но теперь эти новые векторы попарно ортогональны. Нормировав их, мы получим требуемую теоремой систему из $ _j $ ортогонормированных столбцов матрицы $ P $, соответствующих кратному собственному числу $ lambda_j $.

Пример. Диагонализовать матрицу

$$ A=left( begin 0&1&0&1&0&0&0&-1 \ 1&0&1&0&0&0&-1&0 \ 0&1&0&1&0&-1&0&0 \ 1&0&1&0&-1&0&0&0 \ 0&0&0&-1&0&1&0&1 \ 0&0&-1&0&1&0&1&0 \ 0&-1&0&0&0&1&0&1 \ -1&0&0&0&1&0&1&0 end right) $$ с помощью ортогональной матрицы.

Решение. Имеем: $$ det (A-lambda E) equiv (lambda-3)(lambda+3)(lambda-1)^3(lambda+1)^3 , . $$ Ищем собственные векторы. Для простых собственных чисел: $$ lambda_1=-3 Rightarrow mathfrak X_1=left[1,-1,1,,-1,-1,1,-1,1right]^ ; $$ $$ lambda_2=3 Rightarrow mathfrak X_2=left[-1,-1,-1,-1,1,1,1,1right]^ . $$ Эти столбцы войдут в состав матрицы $ P $, только их надо нормировать: $ mathfrak X_ /|mathfrak X_| $. Для кратных собственных чисел $ lambda_j in $ сначала находим произвольные ФСР $$ lambda_3=1 Rightarrow left<begin x_1&-x_2 & &-x_4 & & & &+x_8 & =0 \ & x_2 &-x_3 & +x_4 & & -x_6 & & & =0 \ & & x_3 & +x_4 & & & -x_7 &-x_8& =0 \ & & & 3,x_4 &+x_5 & -x_6 & -2,x_7 & -x_8 & =0 \ & & & & x_5 & -x_6 & +x_7 & -x_8 & =0 end right. $$ $$ Rightarrow mathfrak X_ =left[1,1,0,0,1,1,0,0 right]^ ;mathfrak X_ =left[ 0,-1,0,1,-1,0,1,0 right]^; mathfrak X_ =left[0,1,1,0,1,0,0,1 right]^ . $$ $$ lambda_4=-1 Rightarrow quad left< begin mathfrak X_ =left[-1,1,0,0,-1,1,0,0 right]^\ mathfrak X_ =left[ 0,1,-1,0,-1,0,0,1 right]^ \ mathfrak X_ =left[0,1,0,-1,-1,0,1,0 right]^ end right>, . $$ Применяем к каждой из них алгоритм ортогонализации Грама-Шмидта: $$mathfrak Y_=mathfrak X_=left[1,1,0,0,1,1,0,0 right]^; $$ $$ mathfrak Y_=mathfrak X_+ <coloralpha > mathfrak Y_, quad langle mathfrak Y_,mathfrak Y_ rangle =0 quad Rightarrow <coloralpha >=-frac<langle mathfrak X_,mathfrak Y_ rangle><langle mathfrak Y_,mathfrak Y_ rangle >=frac quad Rightarrow $$ $$ Rightarrow mathfrak Y_=left[frac,-frac,0,1,-frac,frac,1,0 right]^ ; $$ $$ mathfrak Y_=mathfrak X_+ <colorbeta > mathfrak Y_+ <colorgamma > mathfrak Y_, quad langle mathfrak Y_,mathfrak Y_ rangle =0, langle mathfrak Y_,mathfrak Y_ rangle =0 quad Rightarrow $$ $$ <colorbeta > =-frac<langle mathfrak X_,mathfrak Y_ rangle><langle mathfrak Y_,mathfrak Y_ rangle>=-frac, <colorgamma > =-frac<langle mathfrak X_,mathfrak Y_ rangle ><langle mathfrak Y_,mathfrak Y_ rangle >=frac quad Rightarrow $$ $$ Rightarrow mathfrak Y_=left[-frac,frac,1,frac,frac,-frac,frac,1 right]^ , . $$ $$ mathfrak Y_=mathfrak X_=left[-1,1,0,0,-1,1,0,0 right]^, mathfrak Y_=left[frac,frac,-1,0,-frac,-frac,0,1 right]^, $$ $$ mathfrak Y_=left[frac,frac,frac,-1,-frac,-frac,1,-frac right]^ , . $$ После нормирования, составляем из этих векторов ортогональную матрицу: $$ P= left(begin -sqrt/4 & sqrt/4 & 1/2 & sqrt/6 & -sqrt/12 & -1/2 & sqrt/6 & sqrt/12 \ -sqrt/4 & -sqrt/4 & 1/2 & -sqrt/6 & sqrt/12 & 1/2 & sqrt/6 & sqrt/12 \ -sqrt/4 & sqrt/4 & 0 & 0 & sqrt/4 & 0 & -sqrt/3 & sqrt/12 \ -sqrt/4 & -sqrt/4 & 0 & sqrt/3 & sqrt/12 & 0 & 0 & -sqrt/4 \ sqrt/4 & -sqrt/4 & 1/2 & -sqrt/6 & sqrt/12 & -1/2 & -sqrt/6 & -sqrt/12 \ sqrt/4 & sqrt/4 & 1/2 & sqrt/6 & -sqrt/12 & 1/2 & -sqrt/6 & -sqrt/12 \ sqrt/4 & -sqrt/4 & 0 & sqrt/3 & sqrt/12 & 0 & 0 & sqrt/4 \ sqrt/4 & sqrt/4 & 0 & 0 & sqrt/4 & 0 & sqrt/3 & -sqrt/12 end right) , . $$ $$ P^AP= left( begin 3&&&&&&& \ &-3&&&&&& \ &&1&&&&& \ &&&1&&&& \ &&&&1&&& \ &&&&&-1&& \ &&&&&&-1& \ &&&&&&&-1 end right) , . $$ ♦

Видео:7 4 Собственные векторы и собственные значенияСкачать

Квадратичная форма

Экстремальное свойство собственных чисел

Пусть уравнение $ X^<^>A X=1 $ задает эллипсоид в $ mathbb R^3 $, т.е. квадратичная форма положительно определена. Построить посылочный ящик минимального объема (минимальный параллелепипед), содержащий данный эллипсоид.

Решение. Если уравнение эллипсоида приведено к каноническому виду $$ frac+frac+frac=1, $$ то ответ геометрически очевиден: эллипсоид «шире всего» в направлении оси, соответствующей максимальному из трех чисел $ a,b,c $, и «уже всего» в направлении оси, соответствующей минимальному из этих чисел. То есть размер оптимального посылочного ящика — $ (2,a, 2,b, 2,c) $. В случае, если уравнение $ X^<^>A X=1 $ не приведено к каноническому виду, его можно привести к нему с помощью ортогональной замены переменных. Такая замена оставляет инвариантными размеры эллипсоида, а результатом ее становится уравнение эллипсоида в каноническом виде $$ lambda_1 y_1^2+lambda_2 y_2^2+lambda_3 y_3^2=1 , . $$ Здесь $ lambda_1,lambda_2,lambda_3 $ — собственные числа матрицы $ A $, они являются положительными ввиду предположения о положительной определенности этой матрицы. Соответствующие собственные векторы матрицы определяют главные оси эллипсоида 1) . Сравнивая два канонических вида уравнения эллипсоида, можем размеры посылочного ящика сформулировать в терминах собственных чисел матрицы: максимальный размер эллипсоид имеет равным $ 2/sqrt<min > $, а минимальный — равным $ 2/sqrt<max > $. Если эллипсоид нельзя поворачивать вокруг начала координат, то для того, чтобы поместить его в ящик размеров $ 2/sqrt, 2/sqrt, 2/sqrt $ последний надо ориентировать в пространстве: рёбра должны быть параллельны собственным векторам матрицы $ A $. ♦

Замеченное свойство собственных чисел симметричной матрицы распространяется и в многомерное пространство. Традиционно его формулируют в несколько ином виде — хотя и менее наглядном, но более ориентированном на приложения в задачах механики и статистики.

Задача. Найти условные экстремумы квадратичной формы $ F(X)=X^<^>A X $ на единичной сфере $$ mathbb S= , . $$

В курсе математического анализа показывается, что, во-первых, указанные экстремумы существуют 2) , и, во-вторых, могут быть найдены применением метода множителей Лагранжа.

Теорема. Если $ lambda_ $ — максимальное, а $ lambda_ $ — минимальное собственные числа матрицы $ A $, то

$$ max_ X^<^>A X =lambda_, qquad min_ X^<^>A X =lambda_ , . $$ Указанные экстремумы квадратичная форма достигает на соответствующих собственных векторах матрицы $ A $ единичной длины.

Доказательство. Применяем метод множителей Лагранжа, т.е. составляем функцию $$L(X,lambda) = F(X)- lambda (X^X-1)$$ и ищем ее абсолютные экстремумы (как функции $ (n+1) $-го аргумента). На основании теоремы о стационарных точках полинома эти экстремумы должны достигаться на вещественных решениях системы уравнений $$ left< begin big/=&2left(a_x_1+a_x_2+dots+a_x_n right)-2 lambda x_1 &=0, \ dots & & dots \ big/=&2left(a_x_1+a_x_2+dots+a_x_n right)-2 lambda x_n &=0, \ big/=&x_1^2+dots +x_n^2-1 &= 0 , . end right. $$ Решаем эту систему. Первые $ n $ уравнений перепишем в матричном виде $$AX-lambda X=mathbb O iff (A-lambda , E) X=mathbb O , . $$ Из последнего уравнения системы следует, что $ X ne mathbb O $. Следовательно, решениями системы будут исключительно только собственные векторы $ _j $ матрицы $ A $, при $ lambda $ равном соответствующему собственному числу $ lambda_j $ этой матрицы. При $ X=_j $ и $ lambda=lambda_j $ получаем экстремальные значения функции $ F(X) $: $$F(_j)=_j^<^>A _j = lambda_j _j^<^>_j=lambda_j , . $$ Откуда и следует утверждение теоремы. ♦

Еще один вариант экстремального свойства симметричной матрицы излагается ☞ ЗДЕСЬ.