Как построить сечение треугольника (7 видео)

Стереометрия. Задачи на построение сечений

В задачах на построение сечений мы применяем все те определения, теоремы, свойства и признаки, которые изучаем и доказываем на уроках в школе.

Например, если две плоскости имеют общую точку, то они пересекаются по прямой. Это значит, что плоскость сечения и, например, плоскость грани пирамиды будут пересекаться по прямой, и на чертеже будет показана часть этой прямой – отрезок.

Как вы думаете — может ли восьмиугольник быть сечением куба?

И может ли правильный пятиугольник быть сечением куба?

Чтобы соединить какие-либо две точки на чертеже, нам нужна плоскость, в которой эти точки лежат. Иногда это грань объемного тела. Иногда – вспомогательная плоскость.

А вообще сечение — это плоская фигура, которая образуется при пересечении объемного тела плоскостью и граница которой лежит на поверхности этого объемного тела.

Конечно, восьмиугольник сечением куба быть не может. Ведь у куба 6 граней, и поэтому сечение куба не может иметь больше 6 сторон.

При построении сечений мы часто используем следующие теоремы:

1. Линии пересечения параллельных плоскостей третьей плоскостью параллельны.

Именно поэтому правильный пятиугольник не может быть сечением куба. Ведь 4 из 5 сторон этого пятиугольника лежат в параллельных гранях куба и поэтому параллельны. А у правильного пятиугольника параллельных сторон нет.

2. Теорема о прямой и параллельной ей плоскости:

Пусть прямая m параллельна плоскости α. Если плоскость β проходит через прямую m и пересекает плоскость α по прямой c, то c параллельна m.

Эта теорема помогает, например, при построении сечений пирамиды.

Разберем несколько задач на построение сечений.

1. Постройте сечение тетраэдра плоскостью, проходящей через точки М, N, K. Точка М лежит на ребре AD, N — на ребре DC, К — на ребре АВ.

Проведем МК в плоскости грани ABD и MN в плоскости грани ADC.

Продлим отрезки MN и АС;

Проведем РК в плоскости нижней грани; четырехугольник — искомое сечение.

2. Постройте сечение тетраэдра плоскостью, проходящей через точки М, N, K. Точка N лежит на ребре

Покажем, что плоскость сечения пересекает плоскость основания пирамиды по прямой NT, параллельной МК.

Прямая МК параллельна АВ, лежащей в плоскости основания АВС. Значит,

Плоскость сечения проходит прямую МК, параллельную плоскости АВС. По теореме о прямой и параллельной ей плоскости, линия пересечения плоскости сечения и плоскости АВС параллельна прямой МК. Трапеция MKNT — искомое сечение.

3. Постройте сечение куба проходящее через вершину и середины ребер и

Пусть М — середина АВ, N — середина ВС, Продолжим прямую MN до пересечения с продолжениями ребер DC и AD;

Треугольники АМР и KCN — прямоугольные равнобедренные, причем

Проведем — в плоскости задней грани и — в плоскости левой грани куба;

Пятиугольник — искомое сечение. В нем есть параллельные стороны: так как линии пересечения параллельных плоскостей третьей плоскостью параллельны.

4. Постройте сечение куба проходящее через вершину В и середины ребер и

Пусть М — середина ребра , N — середина ребра

Поскольку линии пересечения параллельных плоскостей третьей плоскостью параллельны, плоскость сечения пересекает заднюю грань по прямой, параллельной ВМ, а левую грань — по прямой, параллельной BN. Тогда искомое сечение — ромб

5. Постройте сечение правильного тетраэдра АВСS, проходящее через точку К — середину ребра АВ, точку М, делящую ребро АS в отношении , и точку N — середину апофемы грани SBC.

Пусть SH — апофема грани SBC; N—середина SH.

Проведем MN в плоскости ASH;

Четырехугольник KMEF — искомое сечение.

Постройте сечение правильного тетраэдра АВСS, проходящее через точку К — середину ребра АВ, и точки М и Т — центры граней АSС и SBC.

Пусть SЕ и SH — апофемы граней ASC и SBC; точки М и Т делят отрезки SЕ и SH в отношении 2:1, считая от точки S.

Из подобия треугольников SMT и SEH получим, что Значит

По теореме о прямой и параллельной ей плоскости, линия пересечения плоскости сечения и нижней грани параллельна прямой МТ. Это значит, что плоскость сечения пересекает грань АВС по прямой АВ. Достроим сечение.

7. Постройте сечение куба , проходящее через точку М, лежащую на ребре и точки Т и К, принадлежащие граням АВС и .

Точки М и К лежат в плоскости задней грани . Соединив М и К, получим, что

Соединив точки Р и Т в нижней грани, получим FN — линию пересечения плоскости сечения с нижней гранью;

. Трапеция FMEN — искомое сечение.

8. И самый сложный случай. Построим сечение куба плоскостью МNK, где , причем расстояния от точек М и N до плоскости АВС различны.

Пусть точки и — проекции точек M и N на плоскость нижней грани

Плоскость проходит через параллельные прямые и .

Проведем в этой плоскости MN и

Точки Р и К лежат в нижней грани куба, следовательно, плоскость сечения пересекает нижнюю грань по прямой РК. Дальнейшее построение — очевидно.

Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Построение сечений

Определение

Сечение — это плоская фигура, которая образуется при пересечении пространственной фигуры плоскостью и граница которой лежит на поверхности пространственной фигуры.

Замечание

Для построения сечений различных пространственных фигур необходимо помнить основные определения и теоремы о параллельности и перпендикулярности прямых и плоскостей, а также свойства пространственных фигур. Напомним основные факты.
Для более подробного изучения рекомендуется ознакомиться с темами “Введение в стереометрию. Параллельность” и “Перпендикулярность. Углы и расстояния в пространстве”.

Важные определения

1. Две прямые в пространстве параллельны, если они лежат в одной плоскости и не пересекаются.

2. Две прямые в пространстве скрещиваются, если через них нельзя провести плоскость.

3. Прямая и плоскость параллельны, если они не имеют общих точек.

4. Две плоскости параллельны, если они не имеют общих точек.

5. Две прямые в пространстве называются перпендикулярными, если угол между ними равен (90^circ) .

6. Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.

7. Две плоскости называются перпендикулярными, если угол между ними равен (90^circ) .

Важные аксиомы

1. Через три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

2. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.

3. Через две пересекающиеся прямые проходит плоскость, и притом только одна.

Важные теоремы

1. Если прямая (a) , не лежащая в плоскости (pi) , параллельна некоторой прямой (p) , лежащей в плоскости (pi) , то она параллельна данной плоскости.

2. Пусть прямая (p) параллельна плоскости (mu) . Если плоскость (pi) проходит через прямую (p) и пересекает плоскость (mu) , то линия пересечения плоскостей (pi) и (mu) — прямая (m) — параллельна прямой (p) .

3. Если две пересекающиеся прямых из одной плоскости параллельны двум пересекающимся прямым из другой плоскости, то такие плоскости будут параллельны.

4. Если две параллельные плоскости (alpha) и (beta) пересечены третьей плоскостью (gamma) , то линии пересечения плоскостей также параллельны:

[alphaparallel beta, alphacap gamma=a, betacapgamma=b Longrightarrow aparallel b]

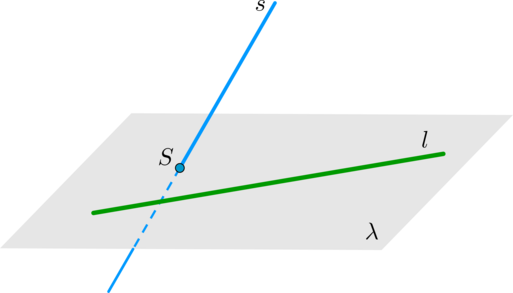
5. Пусть прямая (l) лежит в плоскости (lambda) . Если прямая (s) пересекает плоскость (lambda) в точке (S) , не лежащей на прямой (l) , то прямые (l) и (s) скрещиваются.

6. Если прямая перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости, то она перпендикулярна этой плоскости.

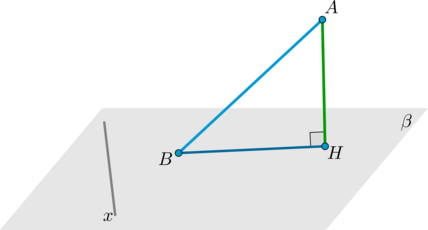
7. Теорема о трех перпендикулярах.

Пусть (AH) – перпендикуляр к плоскости (beta) . Пусть (AB, BH) – наклонная и ее проекция на плоскость (beta) . Тогда прямая (x) в плоскости (beta) будет перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна проекции.

8. Если плоскость проходит через прямую, перпендикулярную другой плоскости, то она перпендикулярна этой плоскости.

Замечание

Еще один важный факт, часто использующийся для построения сечений:

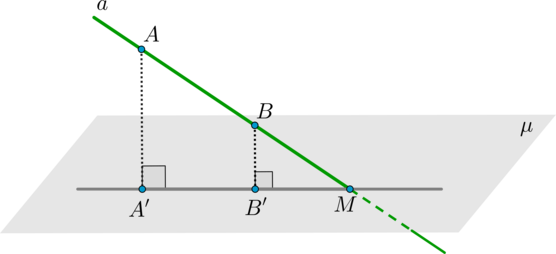
для того, чтобы найти точку пересечения прямой и плоскости, достаточно найти точку пересечения данной прямой и ее проекции на эту плоскость.

Для этого из двух произвольных точек (A) и (B) прямой (a) проведем перпендикуляры на плоскость (mu) – (AA’) и (BB’) (точки (A’, B’) называются проекциями точек (A,B) на плоскость). Тогда прямая (A’B’) – проекция прямой (a) на плоскость (mu) . Точка (M=acap A’B’) и есть точка пересечения прямой (a) и плоскости (mu) .

Причем заметим, что все точки (A, B, A’, B’, M) лежат в одной плоскости.

Пример 1.

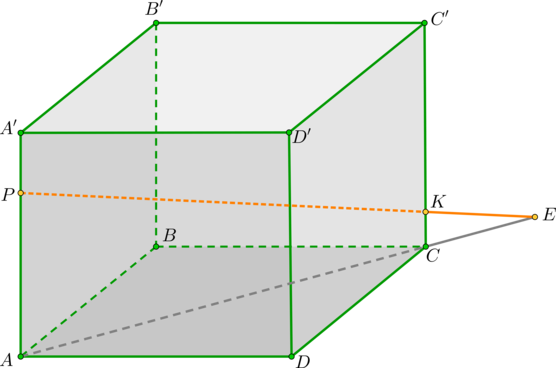
Дан куб (ABCDA’B’C’D’) . (A’P=dfrac 14AA’, KC=dfrac15 CC’) . Найдите точку пересечения прямой (PK) и плоскости (ABC) .

Решение

1) Т.к. ребра куба (AA’, CC’) перпендикулярны ((ABC)) , то точки (A) и (C) — проекции точек (P) и (K) . Тогда прямая (AC) – проекция прямой (PK) на плоскость (ABC) . Продлим отрезки (PK) и (AC) за точки (K) и (C) соответственно и получим точку пересечения прямых – точку (E) .

2) Найдем отношение (AC:EC) . (triangle PAEsim triangle KCE) по двум углам ( (angle A=angle C=90^circ, angle E) – общий), значит, [dfrac=dfrac]

Если обозначить ребро куба за (a) , то (PA=dfrac34a, KC=dfrac15a, AC=asqrt2) . Тогда:

Пример 2.

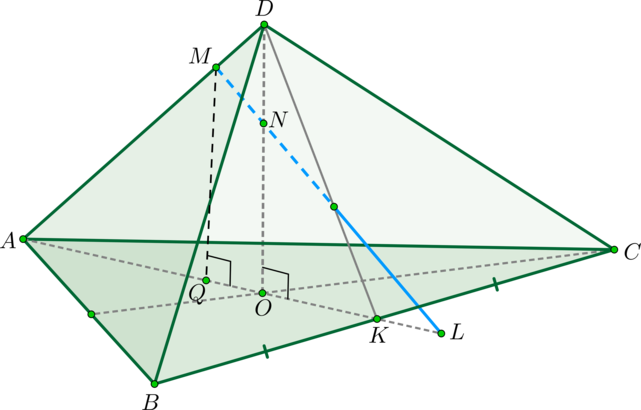
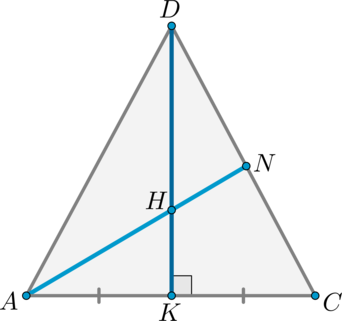
Дана правильная треугольная пирамида (DABC) с основанием (ABC) , высота которой равна стороне основания. Пусть точка (M) делит боковое ребро пирамиды в отношении (1:4) , считая от вершины пирамиды, а (N) – высоту пирамиды в отношении (1:2) , считая от вершины пирамиды. Найдите точку пересечения прямой (MN) с плоскостью (ABC) .

Решение

1) Пусть (DM:MA=1:4, DN:NO=1:2) (см. рисунок). Т.к. пирамида правильная, то высота падает в точку (O) пересечения медиан основания. Найдем проекцию прямой (MN) на плоскость (ABC) . Т.к. (DOperp (ABC)) , то и (NOperp (ABC)) . Значит, (O) – точка, принадлежащая этой проекции. Найдем вторую точку. Опустим перпендикуляр (MQ) из точки (M) на плоскость (ABC) . Точка (Q) будет лежать на медиане (AK) .
Действительно, т.к. (MQ) и (NO) перпендикулярны ((ABC)) , то они параллельны (значит, лежат в одной плоскости). Следовательно, т.к. точки (M, N, O) лежат в одной плоскости (ADK) , то и точка (Q) будет лежать в этой плоскости. Но еще (по построению) точка (Q) должна лежать в плоскости (ABC) , следовательно, она лежит на линии пересечения этих плоскостей, а это – (AK) .

Значит, прямая (AK) и есть проекция прямой (MN) на плоскость (ABC) . (L) – точка пересечения этих прямых.

2) Заметим, что для того, чтобы правильно нарисовать чертеж, необходимо найти точное положение точки (L) (например, на нашем чертеже точка (L) лежит вне отрезка (OK) , хотя она могла бы лежать и внутри него; а как правильно?).

Т.к. по условию сторона основания равна высоте пирамиды, то обозначим (AB=DO=a) . Тогда медиана (AK=dfrac2a) . Значит, (OK=dfrac13AK=dfrac 1a) . Найдем длину отрезка (OL) (тогда мы сможем понять, внутри или вне отрезка (OK) находится точка (L) : если (OL>OK) – то вне, иначе – внутри).

а) (triangle AMQsim triangle ADO) по двум углам ( (angle Q=angle O=90^circ, angle A) – общий). Значит,

[dfrac=dfrac=dfrac=dfrac 45 Rightarrow MQ=dfrac 45a, AQ=dfrac 45cdot dfrac 1a]

Значит, (QK=dfrac2a-dfrac 45cdot dfrac 1a=dfrac7a) .

б) Обозначим (KL=x) .
(triangle LMQsim triangle LNO) по двум углам ( (angle Q=angle O=90^circ, angle L) – общий). Значит,

Следовательно, (OL>OK) , значит, точка (L) действительно лежит вне отрезка (AK) .

Замечание

Не стоит пугаться, если при решении подобной задачи у вас получится, что длина отрезка отрицательная. Если бы в условиях предыдущей задачи мы получили, что (x) – отрицательный, это как раз значило бы, что мы неверно выбрали положение точки (L) (то есть, что она находится внутри отрезка (AK) ).

Пример 3

Дана правильная четырехугольная пирамида (SABCD) . Найдите сечение пирамиды плоскостью (alpha) , проходящей через точку (C) и середину ребра (SA) и параллельной прямой (BD) .

Решение

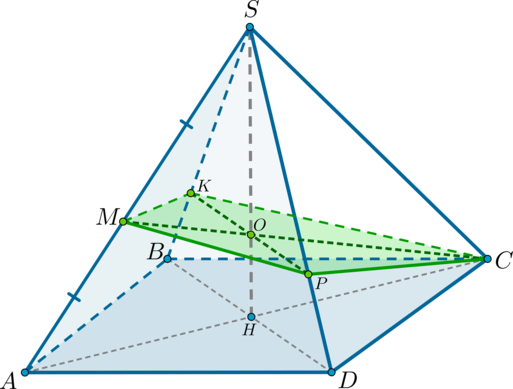
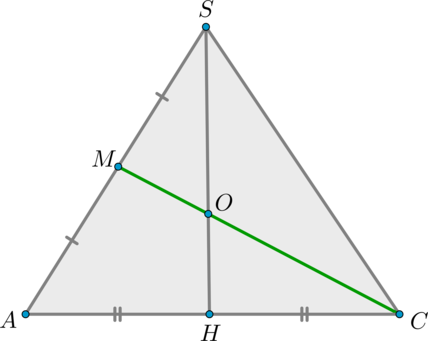
1) Обозначим середину ребра (SA) за (M) . Т.к. пирамида правильная, то высота (SH) пирамиды падает в точку пересечения диагоналей основания. Рассмотрим плоскость (SAC) . Отрезки (CM) и (SH) лежат в этой плоскости, пусть они пересекаются в точке (O) .

Для того, чтобы плоскость (alpha) была параллельна прямой (BD) , она должна содержать некоторую прямую, параллельную (BD) . Точка (O) находится вместе с прямой (BD) в одной плоскости – в плоскости (BSD) . Проведем в этой плоскости через точку (O) прямую (KPparallel BD) ( (Kin SB, Pin SD) ). Тогда, соединив точки (C, P, M, K) , получим сечение пирамиды плоскостью (alpha) .

2) Найдем отношение, в котором делят точки (K) и (P) ребра (SB) и (SD) . Таким образом мы полностью определим построенное сечение.

Заметим, что так как (KPparallel BD) , то по теореме Фалеса (dfrac=dfrac) . Но (SB=SD) , значит и (SK=SP) . Таким образом, можно найти только (SP:PD) .

Рассмотрим (triangle ASC) . (CM, SH) – медианы в этом треугольнике, следовательно, точкой пересечения делятся в отношении (2:1) , считая от вершины, то есть (SO:OH=2:1) .

Теперь по теореме Фалеса из (triangle BSD) : (dfrac=dfrac=dfrac21) .

3) Заметим, что по теореме о трех перпендикулярах (COperp BD) как наклонная ( (OH) – перпендикуляр на плоскость (ABC) , (CHperp BD) – проекция). Значит, (COperp KP) . Таким образом, сечением является четырехугольник (CPMK) , диагонали которого взаимно перпендикулярны.

Пример 4

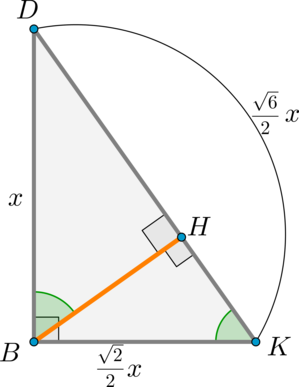
Дана прямоугольная пирамида (DABC) с ребром (DB) , перпендикулярным плоскости (ABC) . В основании лежит прямоугольный треугольник с (angle B=90^circ) , причем (AB=DB=CB) . Проведите через прямую (AB) плоскость, перпендикулярную грани (DAC) , и найдите сечение пирамиды этой плоскостью.

Решение

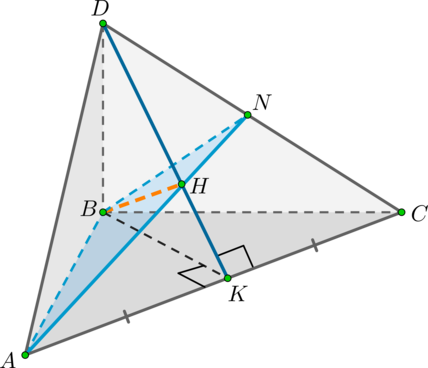
1) Плоскость (alpha) будет перпендикулярна грани (DAC) , если она будет содержать прямую, перпендикулярную (DAC) . Проведем из точки (B) перпендикуляр на плоскость (DAC) — (BH) , (Hin DAC) .

Проведем вспомогательные (BK) – медиану в (triangle ABC) и (DK) – медиану в (triangle DAC) .
Т.к. (AB=BC) , то (triangle ABC) – равнобедренный, значит, (BK) – высота, то есть (BKperp AC) .
Т.к. (AB=DB=CB) и (angle ABD=angle CBD=90^circ) , то (triangle ABD=triangle CBD) , следовательно, (AD=CD) , следовательно, (triangle DAC) – тоже равнобедренный и (DKperp AC) .

Применим теорему о трех перпендикулярах: (BH) – перпендикуляр на (DAC) ; наклонная (BKperp AC) , значит и проекция (HKperp AC) . Но мы уже определили, что (DKperp AC) . Таким образом, точка (H) лежит на отрезке (DK) .

Соединив точки (A) и (H) , получим отрезок (AN) , по которому плоскость (alpha) пересекается с гранью (DAC) . Тогда (triangle ABN) – искомое сечение пирамиды плоскостью (alpha) .

2) Определим точное положение точки (N) на ребре (DC) .

Обозначим (AB=CB=DB=x) . Тогда (BK) , как медиана, опущенная из вершины прямого угла в (triangle ABC) , равна (frac12 AC) , следовательно, (BK=frac12 cdot sqrt2 x) .

Рассмотрим (triangle BKD) . Найдем отношение (DH:HK) .

Заметим, что т.к. (BHperp (DAC)) , то (BH) перпендикулярно любой прямой из этой плоскости, значит, (BH) – высота в (triangle DBK) . Тогда (triangle DBHsim triangle DBK) , следовательно

[dfrac=dfrac Rightarrow DH=dfrac3x Rightarrow HK=dfrac6x Rightarrow DH:HK=2:1]

Рассмотрим теперь (triangle ADC) . Медианы треугольника точной пересечения делятся в отношении (2:1) , считая от вершины. Значит, (H) – точка пересечения медиан в (triangle ADC) (т.к. (DK) – медиана). То есть (AN) – тоже медиана, значит, (DN=NC) .

Видео:Как строить сечения тетраэдра и пирамидыСкачать

Как построить сечение треугольника

Постройте сечение треугольной пирамиды, проходящее через точки M, N и P. Для случая, когда все рёбра пирамиды равны, определите вид треугольника, являющегося сечением.

Точки M и N лежат в одной плоскости, следовательно, через них можем провести прямую. След этой прямой — отрезок MN. Он видимый, тогда соединяем M и N сплошной линией. Аналогично строим след PN. Точки M и P лежат в одной плоскости, следовательно, через них можем провести прямую. След этой прямой — отрезок MP. Он невидимый, поэтому отрезок MP проводим штрихом.Треугольник MNP — искомое сечение:

Так как все ребра пирамиды равны, то треугольник, являющийся сечением — равносторонний остроугольный.