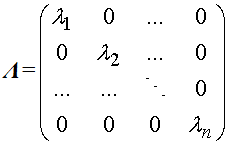Собственные вектора матрицы вольфрам (5 видео)

Собственные вектора матрицы вольфрам

Вычисление собственных чисел матрицы.

Система Mathematica может вычислять собственные значения,даже если в матрице присутствуют символьные параметры. В результате получается компактное представление собственных чисел для любого значения b.

Содержание

Как найти собственные вектора матрицы wolfram mathematica
Посчитать собственные вектора и собственные числа положительно определенной матрицы в NetLink.
Проблема с вычислением собственных значений с помощью математики
2 ответа
WolframAlpha по-русски
Собственные векторы и собственные числа матрицы в Вольфрам Альфа
Собственные векторы матрицы
🔥 Видео

Встроенные функции системы Mathematica разработаны так, что результат вычисления одной функции можно легко использовать в качестве входных данных другой функции.

Здесь в качестве исходных данных функции Plot берется функция собственных значений матрицы, введенной выше.

Можно найти то значение параметра b, при котором первое собственное значение равно нулю.

или посчитать интеграл от 0 до c.

Теперь можно разложить предыдущий результат в ряд.

Или найти численное решение корня уравнения.

Для обработки данных также важно уметь работать с формулами.

Создание списка первых 40 простых чисел.

Приближение аппроксимирующей функцией.

Здесь вычисляется сумма первых 40 простых чисел с помощью аппроксимирующей функции.

А здесь вычисляется точный результат.

Теперь нарисуем график разности между точным и аппроксимирующим результатами, в зависимости от числа слагаемых.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Видео:Собственные значения и собственные векторы матрицы (4)Скачать

Как найти собственные вектора матрицы wolfram mathematica

Видео:КиЯ 0.17 | Списки как векторы и матрицы, элементы линейной алгебры в Wolfram LanguageСкачать

Посчитать собственные вектора и собственные числа положительно определенной матрицы в NetLink.

Собственные числа и вектора матрицы (где ошибка?)
с коефициентом λ=-1 какая-то ересь выходит а вот с остальными все нормально. где ошибка. там.

Найти собственные значения и собственные вектора
Найти собственные значения и собственные вектора. | -3 0 6 | | 8 2 9 | | 4 2 1 |

Как проверить, что ты верно нашел собственные числа и вектора матрицы?
Здравствуйте! Подскажите, пожалуйста, как можно проверить правильность найденных собственных чисел.

Как найти собственные значения и собственные векторы матрицы?
Дано матрица вида A=begin

Найти собственные значения.

Видео:Собственные векторы и собственные числа линейного оператораСкачать

Проблема с вычислением собственных значений с помощью математики

В основном я пытаюсь найти собственные значения для матрицы, и это занимает около 12 часов. Когда он заканчивает, он говорит, что не может найти все собственные векторы (на самом деле их почти нет), и я скептически отношусь к тем, которые он нашел. Все, что я действительно могу сделать, это опубликовать свой код, и я надеюсь, что кто-нибудь сможет сделать мне несколько предложений. Я не очень разбираюсь в математике, и, возможно, медленное время выполнения и плохие результаты как-то связаны со мной, а не со способностями математика. Спасибо всем, кто отвечает, я очень признателен.

Моего кода немного больше, но сейчас он действительно замедляется. Что я должен обязательно упомянуть, так это то, что если я установлю m1 и m2 равными нулю, у меня действительно не будет никаких проблем, но установка m1 на константу заставит все пойти к черту.

2 ответа

Ваша проблема в том, что константа mS остается символической. Это означает, что Mathematica пытается найти собственные значения аналитически, а не численно. Если ваша проблема позволяет вам выбрать числовое значение для mS , сделайте это.

Другая, не связанная с этим проблема заключается в том, что вы используете рекурсивную формулу и хотите использовать, например, мемоизацию в следующей строке

Дополнительный v[n, m] = хранит значение для заданных n и m , поэтому вам не нужно повторять весь путь до v[0,0] каждый раз, когда вызывается h[n, m] в Table[] .

Когда эти две вещи позаботились о моем старом дуэте Core 2, на выполнение собственных значений уходит меньше минуты.

Это продолжение ответа Тимо. Я хочу показать цифру, поэтому помещаю ее в качестве ответа, а не комментария.

Учитывая, что вы хотите найти собственные значения матрицы, содержащей 501 x 501 символических элементов. [Кстати, вы называете их константами, но это неправильное название. Константы — это просто определенные фиксированные значения с именем. То, что вы описываете в своем комментарии к ответу Тимо, является символической переменной.]

Приятно видеть, что делает полностью символьная матрица для вычислений собственных значений. Это для матрицы 2 x 2:

Занимает Array[f, ] // Eigenvalues//ByteCount = 3384 байта. Это довольно быстро взрывается: решение 7×7 уже занимает 70 МБ (на то, чтобы найти это, нужно несколько минут). На самом деле между размером матрицы и количеством байтов можно найти хорошую связь:

Подгоняемая функция: количество байтов = E ^ (2,2403067075863197 + 2,2617380321848457 x размер матрицы).

Как видите, собственные значения символьной матрицы 501 x 501 не будут найдены до конца вселенной.

Видео:Собственные векторы и собственные числа линейного оператораСкачать

WolframAlpha по-русски

Математика с WolframAlpha ® . Объяснения с примерами.

Собственные векторы и собственные числа матрицы в Вольфрам Альфа

Диагональная матрица — это наиболее «удобный» вид матриц, действия с такими матрицами выполняются наиболее просто.

Квадратная невырожденная матрица А порядка n приводится к диагональному виду по формуле

где S — квадратная невырожденная матрица, столбцы которой являются собственными векторами матрицы А, а

— диагональная матрица, по диагонали которой располагаются собственные числа (значения) матрицы А.

Чтобы найти собственные векторы и собственные числа данной квадратной невырожденной матрицы система Вольфрам Альфа предлагает несколько запросов, а также встроенный калькулятор собственных векторов и собственных значений матрицы.

Собственные числа (значения) матрицы

Прежде всего, для отыскания собственных чисел (собственных значений) матрицы можно использовать такой запрос:

Собственные векторы матрицы

Для отыскания собственных векторов исходной матрицы служит такой запрос

Таким образом, получим:

В Вольфрам Альфа можно использовать еще один запрос на отыскание собственных векторов и собственных чисел матрицы, который может оказаться более удобным, поскольку результаты выводятся в наиболее компактном формате:

Калькулятор собственных числе и собственных векторов

Наконец, для отыскания собственных векторов и собственных значений матрицы в Вольфрам Альфа имеется специальный калькулятор:

Видео:ТОП приложение для СТУДЕНТОВ в изучении математики! ChatGPT больше не нужен? Эта программа решит всеСкачать

Собственные векторы матрицы

Онлайн калькулятор нахождение собственных чисел и собственных векторов — Собственный вектор — понятие в линейной алгебре, определяемое для квадратной матрицы или произвольного линейного преобразования как вектор, умножение матрицы на который или применение к которому преобразования даёт коллинеарный вектор — тот же вектор, умноженный на некоторое скалярное значение, называемое собственным числом матрицы или линейного преобразования.

Данный калькулятор поможет найти собственные числа и векторы, используя характеристическое уравнение.