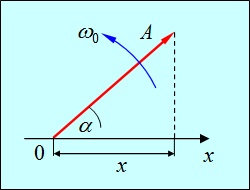
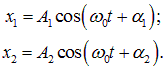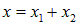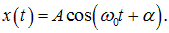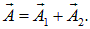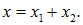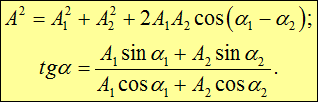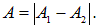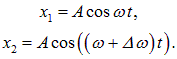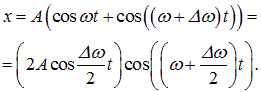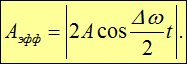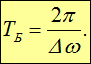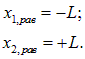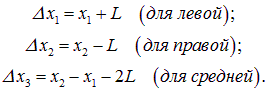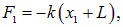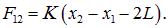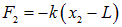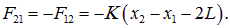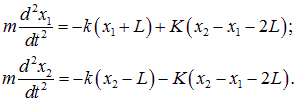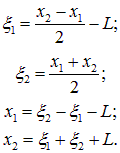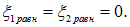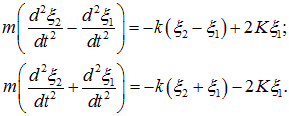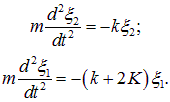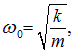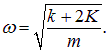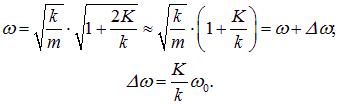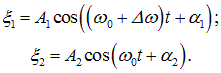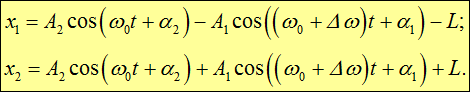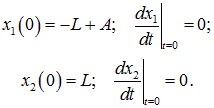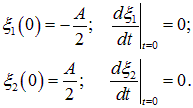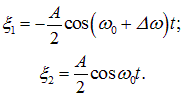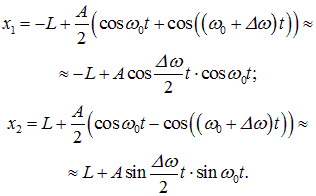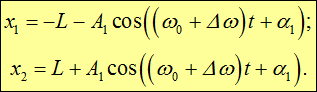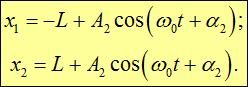Существует очень наглядный геометрический способ представления гармонических колебаний, заключающийся в изображении колебаний в виде векторов на плоскости. Полученная таким образом схема называется векторной диаграммой (рис. 7.4).
 |
Выберем ось 




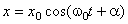
Векторная диаграмма дает возможность свести сложение колебаний к геометрическому суммированию векторов. Рассмотрим сложение двух гармонических колебаний одинакового направления и одинаковой частоты, которые имеют следующий вид:
 |


Представим оба колебания с помощью векторов 
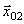




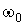

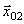
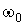


 . . | (7.3) |
Из рис. 7.5 видно, что начальная фаза результирующего колебания будет равна
 . . | (7.4) |
Итак, представление гармонических колебаний посредством векторов дает возможность свести сложение нескольких колебаний к операции сложения векторов. Формулы (7.3) и (7.4) можно, конечно, получить, сложив выражения для 

ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
Во всякой реальной колебательной системе имеются силы сопротивления, действие которых приводит к уменьшению энергии системы. Если убыль энергии не восполняется за счет работы внешних сил, колебания будут затухать. В простейшем, и вместе с тем наиболее часто встречающемся, случае сила сопротивления пропорциональна величине скорости:

где r – постоянная величина, называемая коэффициентом сопротивления. Знак минус обусловлен тем, что сила и скорость имеют противоположные направления; следовательно, их проекции на ось X имеют разные знаки. Уравнение второго закона Ньютона при наличии сил сопротивления имеет вид:
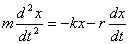
Применив обозначения 

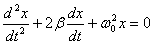
Это уравнение описывает затухающие колебания системы. Коэффициент 
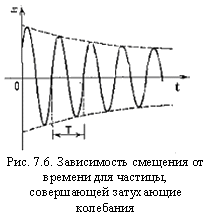 |
Экспериментальный график затухающих колебаний при малом коэффициенте затухания 
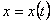
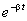

где 
Величина x периодически проходит через нуль и бесконечное число раз достигает максимума и минимума. Промежуток времени между двумя последовательными прохождениями 
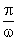


Множитель 
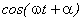



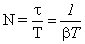
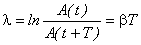
Он связан с числом колебаний 

Величина 

Постоянные величины 

ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
 |
Из-за наличия трения свободные колебания постепенно затухают и через некоторое время прекращаются. Чтобы затухания не было, на колеблющееся тело должно периодически воздействовать какое-либо внешнее тело. Например, волна, поднимающая и опускающая буек (рис. 7.7), рука человека, подталкивающая качели (рис. 7.8). При этом колебания качелей или буйка перестают быть свободными. Их называют вынужденными.
 |
Колебания, совершающиеся под воздействием внешней периодической силы, называются вынужденными. Внешняя сила совершает положительную работу и обеспечивает приток энергии к колебательной системе. Она не дает колебаниям затухать, несмотря на действие сил сопротивления.
Периодическая внешняя сила может изменяться во времени по различным законам. Особый интерес представляет случай, когда внешняя сила, изменяющаяся по гармоническому закону с частотой ω, воздействует на колебательную систему, способную совершать собственные колебания на некоторой частоте ω0. Например, если дергать груз, подвешенный на пружине с частотой 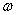
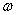
Пусть на систему действует периодическая внешняя сила 
 , , | (7.5) |
где 
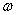


После начала воздействия внешней силы на колебательную систему необходимо некоторое время ωt для установления вынужденных колебаний. В начальный момент в колебательной системе возбуждаются оба процесса – вынужденные колебания на частоте ω и свободные колебания на собственной частоте ω0. Но свободные колебания затухают из-за неизбежного наличия сил трения. Поэтому через некоторое время в колебательной системе остаются только стационарные колебания на частоте ω внешней вынуждающей силы. Время установления по порядку величины равно времени затухания ω свободных колебаний в колебательной системе. Установившиеся вынужденные колебания груза на пружине происходят по гармоническому закону с частотой, равной частоте внешнего воздействия. Можно показать, что в установившемся режиме решение уравнения (7.6) записывается в виде:

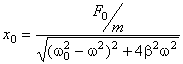

Таким образом, вынужденные колебания представляют собой гармонические колебания с частотой, равной частоте вынуждающей силы. Амплитуда вынужденных колебаний пропорциональна амплитуде вынуждающей силы. Для данной колебательной системы (то есть системы с определенными значениями 

РЕЗОНАНС
Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому, что при некоторой определенной для данной системы частоте амплитуда колебаний достигает максимального значения. Колебательная система оказывается особенно отзывчивой на действие вынуждающей силы при этой частоте. Это явление называется резонансом, а соответствующая частота – резонансной частотой.Графически зависимость амплитуды xm вынужденных колебаний от частоты ω вынуждающей силы описывается резонансной кривой (рис. 7.9).
 |
Исследуем поведение амплитуды вынужденных колебаний в зависимости от частоты 



При возрастании частоты 



Явление резонанса может явиться причиной разрушения мостов, зданий и других сооружений, если собственные частоты их колебаний совпадут с частотой периодически действующей внешней силы. С явлением резонанса приходится считаться при конструировании машин и различного рода сооружений. Собственная частота этих устройств ни в коем случае не должна быть близка к частоте возможных внешних воздействий.
Примеры
 | В январе 1905г. в Петербурге обрушился Египетский мост. Повинны в этом были 9 прохожих, 2 извозчика и 3-й эскадрон Петергофского конногвардейского полка. Произошло следующее. Все солдаты ритмично шагали по мосту. Мост от этого стал раскачиваться – колебаться. По случайному стечению обстоятельств собственная частота колебаний моста совпала с частотой шага солдат. Ритмичный шаг строя сообщал мосту все новые и новые порции энергии. В результате резонанса мост настолько раскачался, что обрушился. Если бы резонанса собственной частоты колебаний моста с частотой шага солдат не было, с мостом ничего бы не случилось. Поэтому при прохождении солдат по слабым мостам принято подавать команду «сбить ногу». |
 | 2 марта 1905 г. в день предстоявшего заседания II Государственной Думы обвалился потолок в главном зале Таврического дворца. Причиной случившегося явилась работа небольшого электровентилятора на чердаке, включенного для проветривания зала перед заседанием Думы. |
 |
Говорят, что великий тенор Энрико Карузо мог заставить стеклянный бокал разлететься вдребезги, спев в полный голос ноту надлежащей высоты. В этом случае звук вызывает вынужденные колебания стенок бокала. При резонансе колебания стенок могут достичь такой амплитуды, что стекло разбивается.
Проделайте опыты
Подойдите к какому-нибудь струнному музыкальному инструменту и громко крикните «а»: какая-то из струн отзовется – зазвучит. Та из них, которая окажется в резонансе с частотой этого звука, будет колебаться сильнее остальных струн – она-то и отзовется на звук.
Натяните горизонтально нетолстую веревку. Закрепите на ней маятник из нити и пластилина. Перекиньте через веревку еще один такой же маятник, но с более длинной ниткой. Длину подвески этого маятника можно изменять, подтягивая рукой свободный конец нитки. Приведите этот маятник в колебательное движение. При этом первый маятник тоже станет колебаться, но с меньшей амплитудой. Не останавливая колебаний второго маятника, постепенно уменьшайте длину его подвески – амплитуда колебаний первого маятника будет увеличиваться. В этом опыте, иллюстрирующем резонанс механических колебаний, первый маятник является приемником колебаний, возбуждаемых вторым маятником. Причиной, вынуждающей первый маятник колебаться, являются периодические колебания веревки с частотой, равной частоте колебаний второго маятника. Вынужденные колебания первого маятника будут иметь максимальную амплитуду лишь тогда, когда его собственная частота совпадает с частотой колебаний второго маятника.
АВТОКОЛЕБАНИЯ
Многочисленны и многообразны создания рук человеческих, в которых возникают и используются автоколебания. Прежде всего, это различные музыкальные инструменты. Уже в глубокой древности – рога и рожки, дудки, свистульки, примитивные флейты. Позже – скрипки, в которых для возбуждения звука используется сила трения между смычком и струной; различные духовые инструменты; гармонии, в которых звук производят металлические язычки, колеблющиеся под действием постоянного потока воздуха; органы, из труб которых вырываются через узкие щели резонирующие столбы воздуха.
 Рис. 7.12 Рис. 7.12 |
Хорошо известно, что сила трения скольжения практически не зависит от скорости. Однако именно благодаря очень слабой зависимости силы трения от скорости звучит скрипичная струна. Качественный вид зависимости силы трения смычка о струну показан на рис. 7.12. Благодаря силе трения покоя струна захватывается смычком и смещается из положения равновесия. Когда сила упругости превысит силу трения, струна оторвется от смычка и устремится к положению равновесия со все возрастающей скоростью. Скорость струны относительно движущегося смычка будет возрастать, сила трения увеличится и в определенный момент станет достаточной для захвата струны. Затем процесс повторится вновь. Таким образом, движущийся с постоянной скоростью смычок вызовет незатухающие колебания струны.
 |
В струнных смычковых инструментах автоколебания поддерживаются силой трения, действующей между смычком и струной, а в духовых инструментах продувание струи воздуха поддерживает автоколебания столба воздуха в трубе инструмента.
Более чем в ста греческих и латинских документах разных времен упоминается пение знаменитого «мемнонского колосса» – величественного звучащего изваяния одного из фараонов, правившего в XIV веке до нашей эры, установленного вблизи египетского города Луксора. Высота статуи около 20 метров, масса достигает тысячи тонн. В нижней части колосса обнаружен ряд щелей и отверстий с расположенными за ними камерами сложной формы. «Мемнонский колосс» представляет собой гигантский орган, звучащий под воздействием естественных потоков воздуха. Статуя имитирует голос человека.
 |
 |
Голос человека – важнейший автоколебательный процесс. В основе его находится движение постоянного потока воздуха из легких, модулируемого колебаниями голосовых связок. Тончайшие фиоритуры колоратурного сопрано из столичного оперного театра и грубый рев быка с точки зрения физики звукообразования совершенно идентичны.
 |
Природные автоколебания несколько экзотического свойства представляют собой поющие пески. Еще в XIV веке великий путешественник Марко Поло упоминал о «звучащих берегах» таинственного озера Лоб-Нор в Азии. За шесть веков поющие пески были обнаружены в различных местах всех континентов. У местного населения они в большинстве случаев вызывают страх, являются предметом легенд и преданий. Джек Лондон так описывает встречу с поющими песками персонажей романа «Сердца трех», отправившихся с проводником на поиски сокровищ древних майя.
«»Когда боги смеются, берегись!» – предостерегающе крикнул старик. Он начертил пальцем круг на песке и, пока он чертил, песок выл и визжал; затем старик опустился на колени, песок взревел и затрубил».
Есть поющие пески и даже целая поющая песчаная гора неподалеку от реки Или в Казахстане. Почти на 300 метров поднялась гора Калкан – гигантский природный орган. По-разному называют ее люди: «поющий бархан», «поющая гора». Сложена она из песка светлых тонов и на фоне темных отрогов Джунгарского Алатау Большого и Малого Калканов представляет необычайное зрелище благодаря цветовому контрасту. При ветре и даже при спуске с нее человека гора издает мелодичные звуки. После дождя и во время штиля гора безмолвствует. Туристы любят посещать Поющий бархан и, поднявшись на одну из трех его вершин, любоваться открывшейся панорамой Или и хребта Заилийского Алатау. Если гора молчит, нетерпеливые посетители «заставляют ее петь». Для этого надо быстро сбежать по наклону горы, песчаные струйки побегут из-под ног, и из недр бархана возникнет гудение.
Много веков прошло со времени обнаружения поющих песков, а удовлетворительного объяснения этому поразительному феномену не было предложено. В последние годы за дело принялись английские акустики, а также советский ученый В.И. Арабаджи. Арабаджи предположил, что излучающий звук верхний слой песка движется при каком-либо постоянном возмущении по нижнему, более твердому слою, имеющему волнистый профиль поверхности. Вследствие сил трения при взаимном перемещении слоев и возбуждается звук.
 |
Вынужденные колебания – это незатухающие колебания. Неизбежные потери энергии на трение при вынужденных колебаниях компенсируются подводом энергии от внешнего источника периодически действующей силы. Существуют системы, в которых незатухающие колебания возникают не за счет периодического внешнего воздействия, а в результате имеющейся у таких систем способности самой регулировать поступление энергии от постоянного источника. Такие системы называются автоколебательными, а процесс незатухающих колебаний в таких системах – автоколебаниями. Схематично автоколебательную систему можно представить в виде источника энергии, осциллятора с затуханием и устройства обратной связи между колебательной системой и источником (рис. 7.10).
В качестве колебательной системы может быть использована любая механическая система, способная совершать собственные затухающие колебания (например, маятник настенных часов). Источником энергии может служить деформированная пружина или груз в поле тяготения. Устройство обратной связи представляет собой некоторый механизм, с помощью которого автоколебательная система регулирует поступление энергии от источника.
 |
Примером механической автоколебательной системы может служить часовой механизм с анкерным ходом (рис. 7.11). В часах с анкерным ходом ходовое колесо с косыми зубьями жестко скреплено с зубчатым барабаном, через который перекинута цепочка с гирей. На верхнем конце маятника закреплен анкер с двумя пластинками из твердого материала, изогнутыми по дуге окружности с центром на оси маятника. В ручных часах гиря заменяется пружиной, а маятник – балансиром, скрепленным со спиральной пружиной. Балансир совершает крутильные колебания вокруг своей оси. Колебательной системой в часах является маятник или балансир, источником энергии – поднятая вверх гиря или заведенная пружина. Устройством, с помощью которого осуществляется обратная связь, является анкер, позволяющий ходовому колесу повернуться на один зубец за один полупериод. Обратная связь осуществляется взаимодействием анкера с ходовым колесом. При каждом колебании маятника зубец ходового колеса толкает анкерную вилку в направлении движения маятника, передавая ему некоторую порцию энергии, которая компенсирует потери энергии на трение. Таким образом, потенциальная энергия гири (или закрученной пружины) постепенно, отдельными порциями передается маятнику.
В обыденной жизни мы, возможно, сами того не замечая, встречаемся с автоколебаниями чаще, чем с колебаниями, вызванными периодическими силами. Автоколебания окружают нас повсюду в природе и технике: паровые машины, двигатели внутреннего сгорания, электрические звонки, часы, звучащая скрипичная струна или органная труба, бьющееся сердце, голосовые связки при разговоре или пении – все эти системы совершают автоколебания.
Проделайте опыт!
 Рис. 7.13 Рис. 7.13 |
Колебательное движение обычно изучают, рассматривая поведение какого-нибудь маятника: пружинного, математического или физического. Все они представляют собой твердые тела. Можно создать устройство, демонстрирующее колебания жидких или газообразных тел. Для этого воспользуйтесь идеей, заложенной в конструкцию водяных часов. Две полуторалитровые пластиковые бутылки соединяют так же, как и в водяных часах, скрепив крышки. Полости бутылок соединяют стеклянной трубкой длиной 15 сантиметров, внутренним диаметром 4-5 миллиметров. Боковые стенки бутылок должны быть ровными и нежесткими, легко сминаться при сдавливании (см. рис. 7.13).
Для запуска колебаний бутылку с водой располагают сверху. Вода из нее начинает сразу же вытекать через трубку в нижнюю бутылку. Примерно через секунду струя самопроизвольно перестает течь и уступает проход в трубке для встречного продвижения порции воздуха из нижней бутылки в верхнюю. Порядок прохождения встречных потоков воды и воздуха через соединительную трубку определяется разницей давлений в верхней и нижней бутылках и регулируется автоматически.
О колебаниях давления в системе свидетельствует поведение боковых стенок верхней бутылки, которые в такт с выпуском воды и впуском воздуха периодически сдавливаются и расширяются. Поскольку
ОБРАЗОВАНИЕ ВОЛН
Как происходит распространение колебаний? Необходима среда для передачи колебаний или они могут передаваться без нее? Как звук от звучащего камертона доходит до слушателя? Каким образом быстропеременный ток в антенне радиопередатчика вызывает появление тока в антенне приемника? Как свет от далеких звезд достигает нашего глаза? Для рассмотрения подобного рода явлений необходимо ввести новое физическое понятие – волна. Волновые процессы представляют общий класс явлений, несмотря на их разную природу.
Источниками волн, будь то морские волны, волны в струне, волны землетрясений или звуковые волны в воздухе, являются колебания. Процесс распространения колебаний в пространстве называется волной. Например, в случае звука колебательное движение совершает не только источник звука (струна, камертон), но также и приемник звука – барабанная перепонка уха или мембрана микрофона. Колеблется и сама среда, через которую распространяется волна.
Волновой процесс обусловлен наличием связей между отдельными частями системы, в зависимости от которых мы имеем упругую волну той или иной природы. Процесс, протекающий в какой-либо части пространства, вызывает изменения в соседних точках системы, передавая им некоторое количество энергии. От этих точек возмущение переходит к смежным с ними и так далее, распространяясь от точки к точке, то есть создавая волну.
Упругие силы, действующие между элементами любого твердого, жидкого или газообразного тела, приводят к возникновению упругих волн. Примером упругих волн является волна, распространяющаяся по шнуру. Если движением руки вверх-вниз возбудить колебания конца шнура, то соседние участки шнура, за счет действия упругих сил связи, также придут в движение, и вдоль шнура будет распространяться волна. Общим свойством волн является то, что они могут распространяться на большие расстояния, а частицы среды совершают колебания лишь в ограниченной области пространства. Частицы среды, в которой распространяется волна, не вовлекаются волной в поступательное движение, они лишь совершают колебания около своих положений равновесия. В зависимости от направления колебаний частиц среды по отношению к направлению распространения волны различают продольные и поперечные волны. В продольной волне частицы среды колеблются вдоль направления распространения волны; в поперечной – перпендикулярно к направлению распространения волны. Упругие поперечные волны могут возникнуть лишь в среде, обладающей сопротивлением сдвигу. Поэтому в жидкой и газообразной средах возможно возникновение только продольных волн. В твердой среде возможно возникновение как продольных, так и поперечных волн.
На рис. 8.1 показано движение частиц при распространении в среде поперечной волны и расположение частиц в волне в четыре фиксированных момента времени. Номерами 1, 2 и т.д. обозначены частицы, отстоящие друг от друга на расстояние, проходимое волной за четверть периода колебаний, совершаемых частицами. В момент времени, принятый за нулевой, волна, распространяясь вдоль оси слева направо, достигла частицы 1, вследствие чего частица начала смещаться из положения равновесия вверх, увлекая за собой следующие частицы. Спустя четверть периода частица 1 достигает крайнего верхнего положения; одновременно начинает смещаться из положения равновесия частица 2. По прошествии еще четверти периода первая частица будет проходить положение равновесия, двигаясь в направлении сверху вниз, вторая частица достигнет крайнего верхнего положения, а третья частица начнет смещаться вверх из положения равновесия. В момент времени, равный 

На рис. 8.2 показано движение частиц при распространении в среде продольной волны. Все рассуждения, касающиеся поведения частиц в поперечной волне, могут быть отнесены и к данному случаю с заменой смещений вверх и вниз смещениями вправо и влево. Из рис. 8.2 видно, что при распространении продольной волны в среде создаются чередующиеся сгущения и разрежения частиц, перемещающиеся в направлении распространения волны со скоростью 
Тела, которые воздействуют на среду, вызывая колебания, называются источниками волн. Распространение упругих волн не связано с переносом вещества, но волны переносят энергию, которой обеспечивает волновой процесс источник колебаний.
Геометрическое место точек, до которых доходят возмущения к данному моменту времени, называется фронтом волны. То есть фронт волны представляет собой ту поверхность, которая отделяет часть пространства, уже вовлеченного в волновой процесс, от области, которую возмущения еще не достигли.
Геометрическое место точек, колеблющихся в одинаковых фазах, называется волновой поверхностью. Волновую поверхность можно провести через любую точку пространства, охваченного волновым процессом. Волновые поверхности могут иметь любую форму. В простейших случаях они имеют форму плоскости или сферы. Соответственно волна в этих случаях называется плоской или сферической. В плоской волне волновые поверхности представляют собой множество параллельных друг другу плоскостей; в сферической волне – множество концентрических сфер.
Расстояние, на которое распространяется волна за время, равное периоду колебаний частиц среды, называется длиной волны. Очевидно, что 

На рис. 8.3, выполненным с помощью компьютерной графики, приведена модель распространения поперечной волны на воде от точечного источника. Каждая частица совершает гармонические колебания около положения равновесия.
Рис. 8.3. Распространение поперечной волны от точечного источника колебаний
Видео:Урок 337. Сложение колебаний одной частоты. Метод векторных диаграммСкачать

Сложение колебаний. Векторные диаграммы
Пусть некоторая физическая величина изменяется со временем так, что это изменение описывается суммой функций
В таком случае величина (9.42) называется суммой однонаправленных гармонических колебаний одинаковой частоты. Покажем, что эта сумма также является гармоническим колебанием той же частоты.
Для этого, применяя тригонометрическое тождество
преобразуем выражение (9.42) следующим образом:
Возведем каждое из уравнений (9.46) в квадрат и сложим полученные равенства. В результате придем к соотношению
Так как выражение в круглых скобках есть cos (ai — i —u>2)t ) изменяется медленнее, чем функция cos ( +u>2) t ), зависимость (9.50) можно рассматривать как * гармо
ническое” колебание частоты и = y(u>i +^2) с переменной амплитудой
График зависимости (9.50) представлен на рис. 9.11. Такие колебания называют биениями.
Движение точки на плоскости описывается двумя функциями: х = x(t) и у = y(t). Когда эти функции представляют собой гармонические колебания
говорят о сложении взаимно перпендикулярных колебаний.
Соотношения (9.51) есть записанные в параметрической форме уравнения кривой на плоскости. Когда отношение частот и а>2 есть рациональное число, т.е. может быть представлено в виде дроби
где ni и П2 ” целые числа, такие кривые называются фигурами Лиссажу. Эти фигуры заключены в прямоугольнике, определяемом неравенствами
Рассмотрим простейшие из фигур Лиссажу.
1. Положим в формулах (9.51)
Нетрудно видеть, что при этом
Таким образом, функции (9.52) описывают колебательное движение точки на плоскости ху, траекторией которого является отрезок прямой, проходящей через начало координат (рис. 9.12).
Рис. 9.12. Фигура Лиссажу
В этом случае функции (9.51) принимают вид
Используя основное тригонометрическое тождество


Рис. 9.13. Фигура Лиссажу 3. Наконец, рассмотрим случай, когда
При этом функции (9.51) превращаются в
Применяя тригонометрическое тождество
придем к уравнению траектории
В этом случае точка совершает колебательное движение, перемещаясь в плоскости ху по параболе (рис. 9.14) из точки А в точку В и обратно.
Видео:67. Сложение колебанийСкачать

1.4. Сложение колебаний одного направления
Может случиться так, что осциллятор принимает участие в двух одинаково направленных колебаниях с разными амплитудами, частотами и начальными фазами. Рассмотрим сложение таких колебаний.
Сложение колебаний с одинаковыми частотами
Для простоты рассмотрим сначала случай, когда частоты складываемых колебаний одинаковы. Общие решения складываемых гармонических колебаний имеют вид:
где x1, x2 — переменные, описывающие колебания, A1, A2 — их амплитуды, а 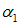
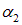
удобно найти с помощью векторной диаграммы. Этот метод использует аналогию между вращением и колебательным процессом.
Возьмем общее решение (1.23) для гармонического колебания. Выберем ось 0x. Из точки 0 отложим вектор длиной A, образующий с осью 0x угол 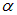
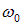
Таким образом, проекция конца вектора на ось 0x будет совершать гармонические колебания с амплитудой, равной длине вектора, с круговой частотой, равной угловой скорости вращения вектора, и с начальной фазой, равной углу, образуемому вектором с осью в начальный момент времени (рис. 1.12).
Рис. 1.12. Векторная диаграмма для общего решения (1.23)
Применим теперь эту технику к сложению колебаний (1.34). Представим оба колебания с помощью векторов А1 и А2 Возьмем их векторную сумму (рис. 1.13)
Рис. 1.13. Векторная диаграмма для сложения одинаково направленных колебаний одинаковой частоты
Проекция вектора А1 на ось 0x равна сумме проекций соответствующих векторов
Таким образом, вектор А представляет собой результирующее колебание. Этот вектор вращается с той же угловой скоростью 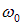
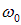
В частности, если фазы складываемых колебаний равны или отличаются на величину, кратную 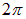
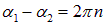
Если же складываемые колебания находятся в противофазе (то есть 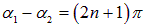
Биения
В этом разделе мы рассмотрим случай сложения одинаково направленных гармонических колебаний с разными частотами. На практике особый интерес представляет случай, когда складываемые колебания мало отличаются по частоте. Как мы увидим, в результате сложения этих колебаний получаются колебания с периодически изменяющейся амплитудой, называемые биениями.
Биения — это периодическое изменение амплитуды колебаний, возникающее при сложении двух гармонических колебаний с близкими частотами.
Для простоты рассмотрим случай, когда амплитуды складываемых колебаний равны A, а начальные фазы обоих колебаний равны нулю. Частоты складываемых колебаний равны, соответственно, 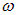
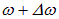
Складываем эти выражения и учитываем известную формулу тригонометрии:
Если 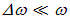
Кроме того, множитель в скобках меняется медленно по сравнению с 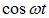
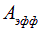
Подчеркнем, что в строгом смысле такое колебание не является гармоническим, и еще раз напомним, что, согласно определению, колебание гармоническое, если оно происходит по закону 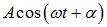
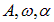
Рис. 1.14. Биения при сложении колебаний с близкими частотами
Частота пульсаций амплитуды (ее называют частотой биений) равна разности частот складываемых колебаний. Период биений равен
Колебания двух связанных осцилляторов
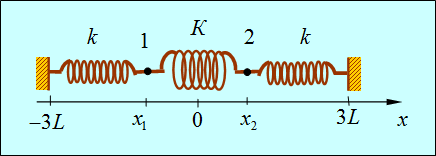
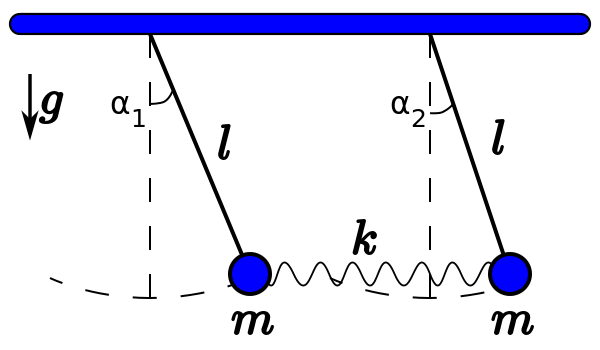
Приведем поучительный пример системы, в которой возникают биения. Рассмотрим два груза массой m, которые могут колебаться под действием двух одинаковых пружин с коэффициентами жесткости k. Пусть грузы соединены также мягкой пружиной с коэффициентом жесткости K<<k. Будем полагать длины всех пружин в нерастянутом состоянии одинаковыми и равными 2L (рис. 1.15).
Рис. 1.15. Пример связанных осцилляторов.
Колебания происходят вдоль оси 0х, сила тяжести не учитывается
Тогда в положении равновесия координаты грузов равны
При колебаниях координаты равны, соответственно, x1(t), x2(t). Удлинения пружин записываются как
Мы имеем дело с системой с двумя степенями свободы. Составим уравнения движения. На первый груз действуют сила со стороны пружины k, равная
и сила со стороны пружины K, равная
На второй груз действуют аналогичные силы
Соответственно, уравнения движения имеют вид
Эти уравнения не слишком похожи на первый взгляд на уравнения гармонических колебаний, потому что на колебания x1 оказывают влияния колебания x2 и наоборот. Поэтому преобразуем уравнения к новым переменным, уравнения для которых были бы независимыми (такие переменные называют нормальными координатами, а соответствующие им колебания — нормальными колебаниями (модами)). Именно, введем новые переменные x1 и x2:
Как легко убедиться, положениям равновесия соответствуют нулевые значения этих координат
В этих переменных уравнения (1.42) принимают вид:
Складывая и вычитая эти уравнения, приходим к паре независимых уравнений для введенных нормальных координат:
Первое уравнение описывает гармонические колебания с частотой
совпадающей с частотой колебаний пружинных маятников в отсутствие соединительной пружины К. Второе уравнение описывает колебания со сдвинутой частотой
Соответственно, мы получаем общее решение системы уравнений:
Общее решение для координат х1 и х2 колеблющихся точек следуют из (1.47) и (1.43):
Для примера рассмотрим случай, когда первая масса смещается на расстояние 
Этому соответствуют следующие начальные значения нормальных координат:
Такие начальные условия уже рассматривались выше. Соответствующие им решения имеют вид
Подставляя найденные амплитуды и начальные фазы в (1.48), получаем решения, описывающие колебания рассматриваемых масс около их положений равновесия:
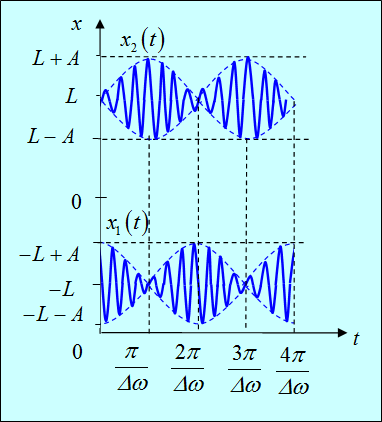
Графики функций x1(t), x2(t) показаны на рис. 1.16. Видна характерная картина биений.
Рис. 1.16. Биения в системе двух связанных осцилляторов
В начальный момент времени колеблется лишь первый груз. Затем начинает колебаться второй, а амплитуда колебаний первого уменьшается. Через время 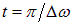
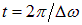
На рис. 1.17 демонстрируются биения в системе двух связанных математических маятников.
Рис. 1.17. Биения в системе связанных маятников
Выясним теперь физический смысл нормальных мод, соответствующих чисто гармоническим колебаниям системы. Если возбуждены колебания только первой из них (x1), то A2 = 0 и, как следует из общего решения (1.48),
Из (1.53) видно, что первая нормальная мода соответствует такому колебанию, когда оба груза смещаются на одинаковые расстояния от их положений равновесия, но в противоположные стороны, другими словами — они колеблются в противофазе. Скорости движения грузов также равны по величине и противоположны по направлению, так что центр масс грузов остается неподвижным. Колебания происходят под действием пружин с жесткостью k, к которым добавляется соединительная пружина с жесткостью К. Как следствие, частота таких колебаний больше частоты колебаний несвязанных осцилляторов
Возбуждение только второй (x2) нормальной моды означает, что A1 = 0:
В этом случае грузы смещаются из положения равновесия в одну сторону на одинаковые расстояния, другими словами – они колеблются синфазно. Скорости их также одинаковы по величине и направлению. Соединительная пружина колеблется вместе с грузами, но остается не растянутой и потому не оказывает влияния, так что частота колебаний совпадает с частотой колебаний несвязанных маятников.
В разобранном случае мы познакомились с нормальными модами и выяснили, что их частоты сдвигаются по сравнению с частотами колебаний несвязанных маятников. Любое другое колебательное движение системы можно представить как суперпозицию нормальных мод. Аналогичным образом можно рассмотреть цепочку из множества связанных друг с другом осцилляторов и изучить их нормальные колебания. Такая система представляет собой модель кристаллической решетки.
🎬 Видео
Сложение N колебаний методом векторных диаграммСкачать

Построение векторных диаграмм/Треугольник токов, напряжений и мощностей/Коэффициент мощностиСкачать

Сложение векторов. Правило параллелограмма. 9 класс.Скачать

Сложение векторов. 9 класс.Скачать

Сложение колебанийСкачать

Урок 336. Векторное представление колебанийСкачать

Урок 338. Сложение колебаний близких частот. БиенияСкачать

Векторные диаграммы и коэффициент мощностиСкачать

Урок 342. Сложение взаимно перпендикулярных колебаний. Фигуры ЛиссажуСкачать

8 класс, 44 урок, Законы сложения векторов. Правило параллелограммаСкачать

Векторная диаграммаСкачать

Сложение взаимно перпендикулярных гармонических колебанийСкачать

Урок 340. Сложение колебаний кратных частот. Гармонический анализ и синтезСкачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Урок 8. Векторные величины. Действия над векторами.Скачать

Построение векторной диаграммы. Цепь RLCСкачать