Сколько точек с целыми координатами на окружности

Видео:Как искать точки на тригонометрической окружности.Скачать

Числовая окружность

В этой статье мы очень подробно разберем определение числовой окружности, узнаем её главное свойство и расставим числа 1,2,3 и т.д. Про то, как отмечать другие числа на окружности (например, (frac , frac , frac , 10π, -frac )) разбирается в этой статье .

Числовой окружностью называют окружность единичного радиуса, точки которой соответствуют действительным числам , расставленным по следующим правилам:

1) Начало отсчета находится в крайней правой точке окружности;

2) Против часовой стрелки — положительное направление; по часовой – отрицательное;

3) Если в положительном направлении отложить на окружности расстояние (t), то мы попадем в точку со значением (t);

4) Если в отрицательном направлении отложить на окружности расстояние (t), то мы попадем в точку со значением (–t).

Почему окружность называется числовой?
Потому что на ней обозначаются числа. В этом окружность похожа на числовую ось – на окружности, как и на оси, для каждого числа есть определенная точка.

Зачем знать, что такое числовая окружность?
С помощью числовой окружности определяют значение синусов, косинусов, тангенсов и котангенсов. Поэтому для знания тригонометрии и сдачи ЕГЭ на 60+ баллов, обязательно нужно понимать, что такое числовая окружность и как на ней расставить точки.

Что в определении означают слова «…единичного радиуса…»?
Это значит, что радиус этой окружности равен (1). И если мы построим такую окружность с центром в начале координат, то она будет пересекаться с осями в точках (1) и (-1).

Ее не обязательно рисовать маленькой, можно изменить «размер» делений по осям, тогда картинка будет крупнее (см. ниже).

Почему радиус именно единица? Так удобнее, ведь в этом случае при вычислении длины окружности с помощью формулы (l=2πR) мы получим:

Длина числовой окружности равна (2π) или примерно (6,28).

А что значит «…точки которой соответствуют действительным числам»?
Как говорили выше, на числовой окружности для любого действительного числа обязательно найдется его «место» — точка, которая соответствует этому числу.

Зачем определять на числовой окружности начало отсчета и направления?
Главная цель числовой окружности — каждому числу однозначно определить свою точку. Но как можно определить, где поставить точку, если неизвестно откуда считать и куда двигаться?

Тут важно не путать начало отсчета на координатной прямой и на числовой окружности – это две разные системы отсчета! А так же не путайте (1) на оси (x) и (0) на окружности – это точки на разных объектах.

Видео:14 Количество точек с целыми координатами в круге данного радиусаСкачать

Какие точки соответствуют числам (1), (2) и т.д?

Помните, мы приняли, что у числовой окружности радиус равен (1)? Это и будет нашим единичным отрезком (по аналогии с числовой осью), который мы будем откладывать на окружности.

Чтобы отметить на числовой окружности точку соответствующую числу 1, нужно от 0 пройти расстояние равное радиусу в положительном направлении.

Чтобы отметить на окружности точку соответствующую числу (2), нужно пройти расстояние равное двум радиусам от начала отсчета, чтобы (3) – расстояние равное трем радиусам и т.д.

При взгляде на эту картинку у вас могут возникнуть 2 вопроса:
1. Что будет, когда окружность «закончится» (т.е. мы сделаем полный оборот)?
Ответ: пойдем на второй круг! А когда и второй закончится, пойдем на третий и так далее. Поэтому на окружность можно нанести бесконечное количество чисел.

2. Где будут отрицательные числа?
Ответ: там же! Их можно так же расставить, отсчитывая от нуля нужное количество радиусов, но теперь в отрицательном направлении.

К сожалению, обозначать на числовой окружности целые числа затруднительно. Это связано с тем, что длина числовой окружности будет равна не целому числу: (2π). И на самых удобных местах (в точках пересечения с осями) тоже будут не целые числа, а доли числа (π) : ( frac ),(-frac ),(frac ), (2π). Поэтому при работе с окружностью чаще используют числа с (π). Обозначать такие числа гораздо проще (как это делается можете прочитать в этой статье ).

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Главное свойство числовой окружности

Одному числу на числовой окружности соответствует одна точка, но одной точке соответствует множество чисел.

Такая вот математическая полигамия.

И следствие из этого правила:

Все значения одной точки на числовой окружности можно записать с помощью формулы:

Если хотите узнать логику этой формулы, и зачем она нужна, посмотрите это видео .

В данной статье мы рассмотрели только теорию о числовой окружности, о том как расставляются точки на числовой и окружности и принципе, как с ней работать вы можете прочитать здесь .

Что надо запомнить про числовую окружность:

Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Тригонометрические уравнения

Решение простейших тригонометрических уравнений

Градусы и радианы

Знакомство с тригонометрической окружностью

Повороты на тригонометрической окружности

Как много боли связано со словом тригонометрия. Эта тема появляется в 9 классе и уже никуда не исчезает. Тяжело приходится тем, кто чего-то не понял сразу. Попробуем это исправить, чтобы осветить ваше лицо улыбкой при слове тригонометрия или хотя бы добиться «poker face».

Начнем с того, что как длину можно выразить в метрах или милях, так и угол можно выразить в радианах или градусах .

1 радиан = 180/π ≈ 57,3 градусов

Но проще запомнить целые числа: 3,14 радиан = 180 градусов. Это все одно и то же значение числа π.

Вспомним, что если нас просят развернуться, то нам нужно повернуться на 180 градусов, а теперь можно так же сказать: Повернись на π!

О графиках синуса, косинуса и тангеса поговорим в другой статье.

А сейчас начем с декартовой (прямоугольной) системы координат.

Раньше она помогала строить графики, а теперь поможет с синусом и косинусом.

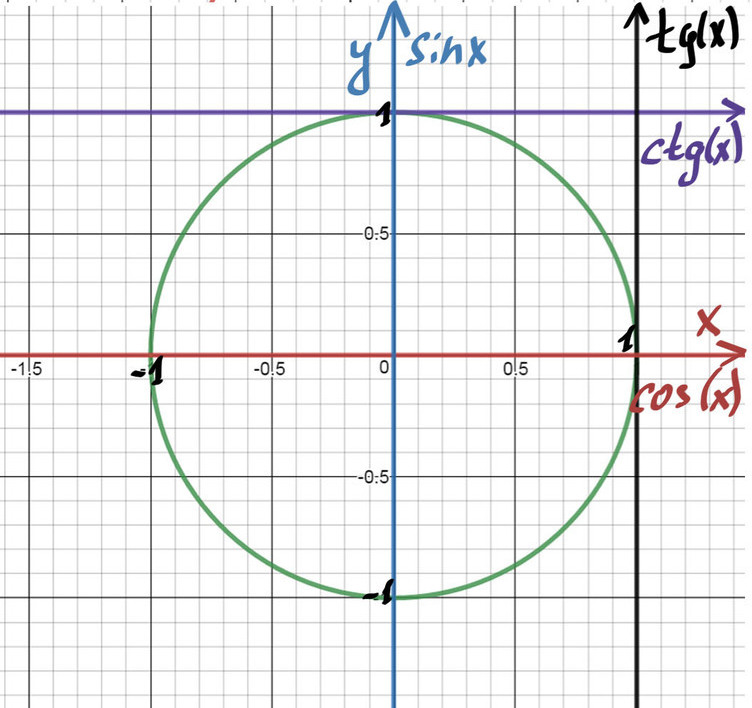
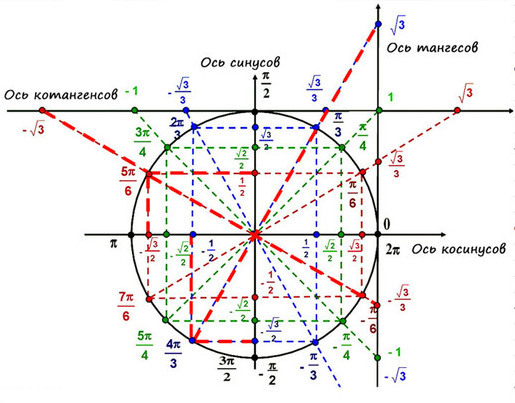
На пересечении оси Х и оси Y построим единичную (радиус равен 1) окружность:

Тогда ось косинусов будет совпадать с х, ось синусов с y. Оси тангенсов и котангенсов также показаны на рисунке.

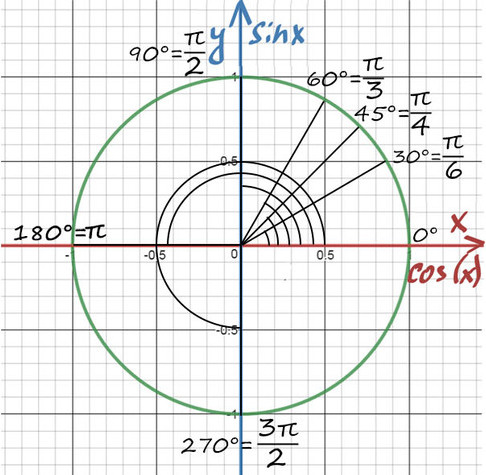
А теперь отметим основные значения градусов и радиан на окружности.

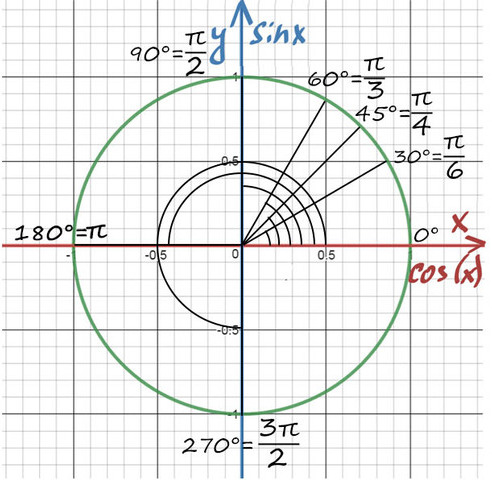
Давай договоримся с тобой, как взрослые люди: на окружности мы будем отмечать угол в радианах, то есть через Пи.

Достаточно запомнить, что π = 180° (тогда π/6 = 180/6 = 30°; π/3 = 180/3 = 60°; π/4 = 180/4 = 45°).

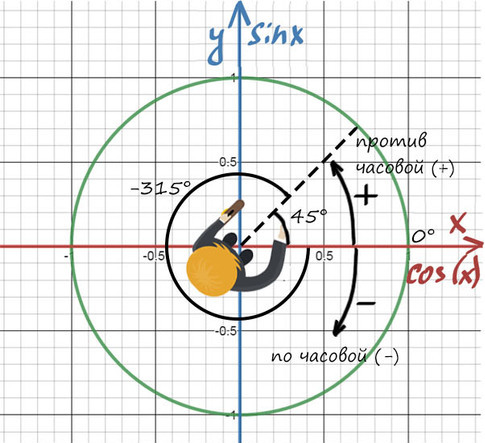
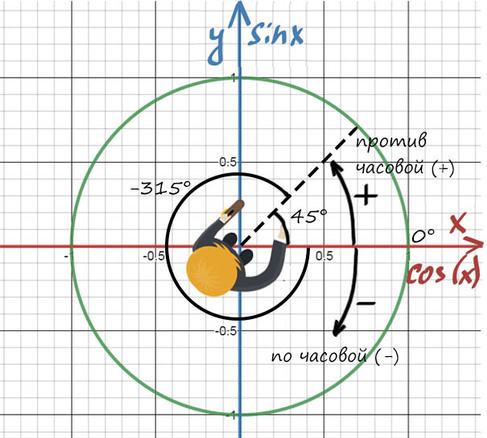
А теперь давай покрутимся на окружности! За начало отчета принято брать крайнюю правую точку окружности (где 0°):

От нее задаем дальнейший поворот. Вращаться можем как в положительную сторону (против часовой), так и в отрицательную сторону (по часовой стрелке).

Повернуться на 45° можно двумя спобами: через левое плечо на 45° в (+) сторону, либо через правое плечо на 315° в (-).

Главное — направление, куда мы будем смотреть, а не угол!

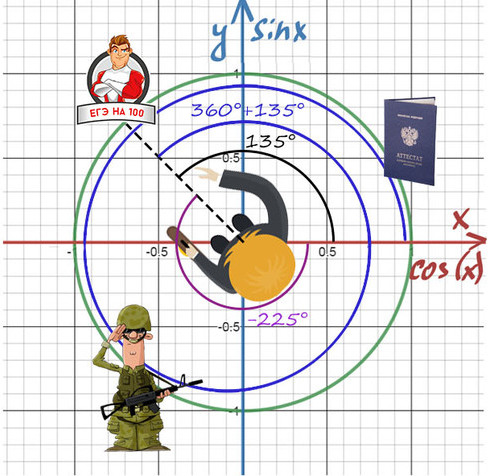
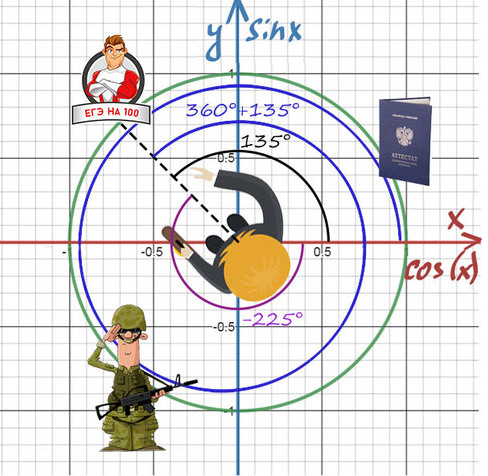
Нужно направить пунктир на 100 баллов, а сколько оборотов и в какую сторону вокруг себя мы сделаем — без разницы!

Получить 100 баллов можно поворотом на 135° или 360°+135°, или -225°, или -225°-360°.

А теперь у тебя есть два пути:

Выучить всю окружность (тригонометр). Неплохой вариант, если с памятью у тебя все отлично, и ничего не вылетит из головы в ответственный момент:

А можно запомнить несколько табличных углов и соответствующие им значения, а потом использовать их.

Находите равные углы (вертикальные, соответственные) на тригонометрической окружности. Попасть в любую точку можно с помощью суммы или разности двух табличных значений.

Сразу попробуем разобрать на примере:

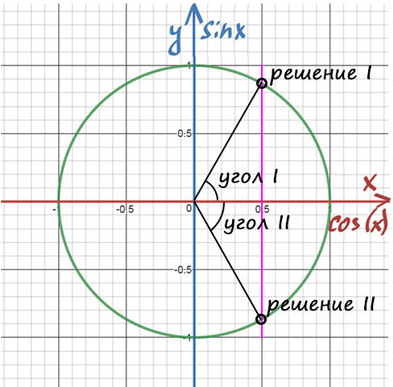
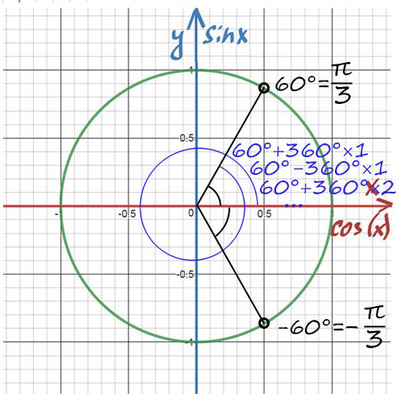
1) Помним, что ось cos(x) — это горизонтальная ось. На ней отмечаем значение ½ и проводим перпендикулярную (фиолетовую) прямую до пересечений с окружностью.

2) Получили две точки пересечения с окружностью, значение этих углов и будет решением уравнения.

Дело за малым — найти эти углы.

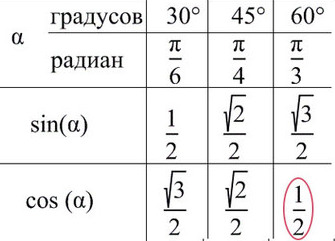
Лучше обойтись «малой кровью» и выучить значение синуса и косинуса для углов от 30° до 60°.

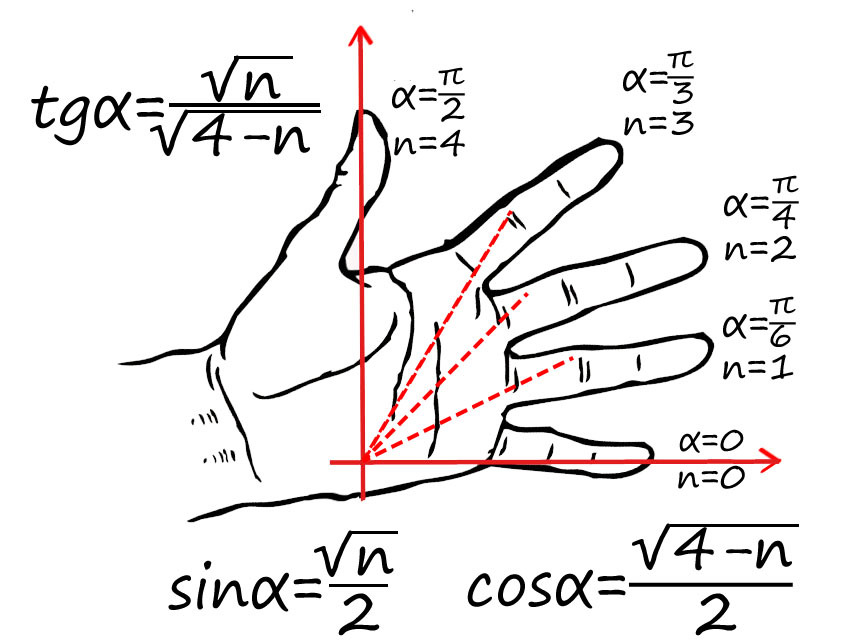
Или запомнить такой прием:

Пронумеруй пальцы от 0 до 4 от мизинца до большого. Угол задается между мизинцем и любым другим пальцем (от 0 до 90).

Например, требуется найти sin(π/2) : π/2 — это большой палец, n = 4 подставляем в формулу для синуса: sin(π/2) = √4/2 = 1 => sin(π/2) = 1.

cos(π/4) — ? π/4 соответсвует среднему пальцу (n = 2) => cos(π/4) = √2/2.

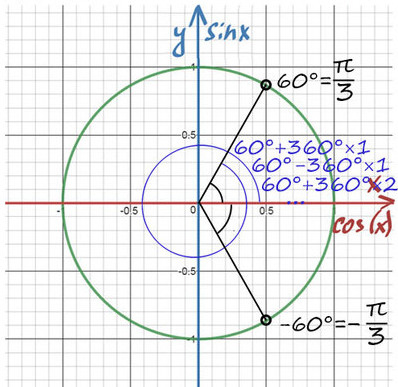
При значении cos(x) = ½ из таблицы или с помощью мнемонического правила находим x = 60° (первая точка x = +π/3 из-за того, что поворот происходил против часовой стерелки (+), угол показан черной дугой).

Вторая же точка соответствует точно такому же углу, только поворот будет по часовой стрелке (−). x = −π/3 (угол показан нижней черной дугой).

И последнее, прежде чем тебе, наконец, откроются тайные знания тригонометрии:

Когда требуется попасть в «100 баллов», мы можем в них попасть с помощью поворота на . =-225°=135°=495°=.

То же самое и здесь! Разные углы могут отражать одно и то же направление.

Абсолютно точно можно сказать, что нужно повернуться на требуемый угол, а дальше можно поворачиваться на 360° = 2π (синим цветом) сколько угодно раз и в любом направлении.

Таким образом, попасть в первое направление 60° можно: . 60°-360°, 60°, 60°+360°.

И как записать остальные углы, не записывать же бесконечное количество точек? (Хотел бы я на это посмотреть☻)

Поэтому правильно записать ответ: x = 60 + 360n, где n — целое число (n∈Ζ) (поворачиваемся на 60 градусов, а после кружимся сколько угодно раз, главное, чтобы направление осталось тем же). Аналогично x = −60 + 360n.

Но мы же договорились, что на окружности все записывают через π, поэтому cos(x) = ½ при x = π/3 + 2πn, n∈Ζ и x = −π/3 + 2πk, k∈Ζ.

Ответ: x = π/3 + 2πn, x= − π/3 + 2πk, (n, k) ∈Ζ.

Пример №2. 2sinx = √2

Первое, что следует сделать, это перенести 2-ку вправо => sinx=√2/2

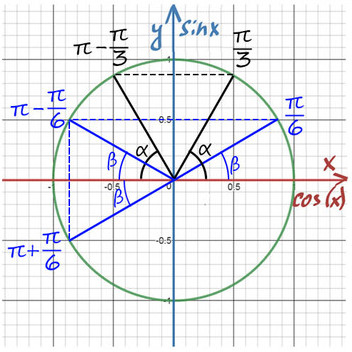
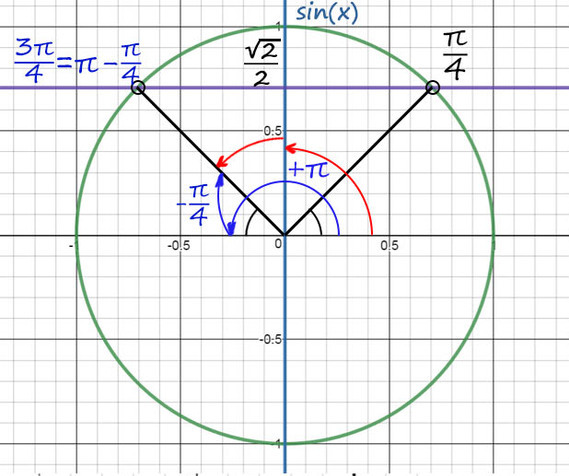
1) sin(x) совпадает с осью Y. На оси sin(x) отмечаем √2/2 и проводим ⊥ фиолетовую прямую до пересечений с окружностью.

2) Из таблицы sinx = √2/2 при х = π/4, а вторую точку будем искать с помощью поворота до π, а затем нужно вернуться обратно на π/4.

Поэтому вторая точка будет x = π − π/4 = 3π/4, в нее также можно попасть и с помощью красных стрелочек или как-то по-другому.

И еще не забудем добавить +2πn, n∈Ζ.

Ответ: 3π/4 + 2πn и π/4 + 2πk, k и n − любые целые числа.

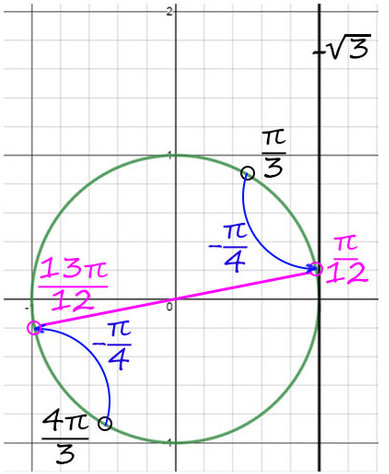
Пример №3. tg(x + π/4) = √3

Вроде все верно, тангенс равняется числу, но смущает π/4 в тангенсе. Тогда сделаем замену: y = x + π/4.

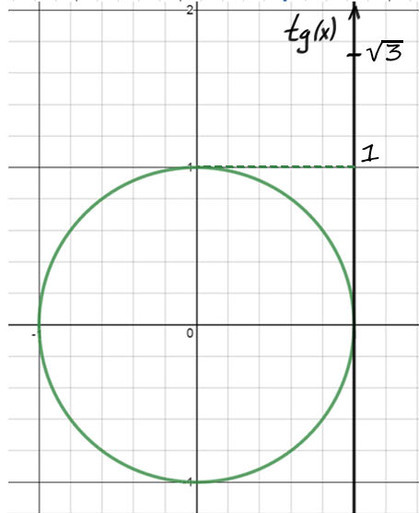
tg(y) = √3 выглядит уже не так страшно. Вспомним, где ось тангенсов.

1) А теперь на оси тангенсов отметим значение √3, это выше чем 1.

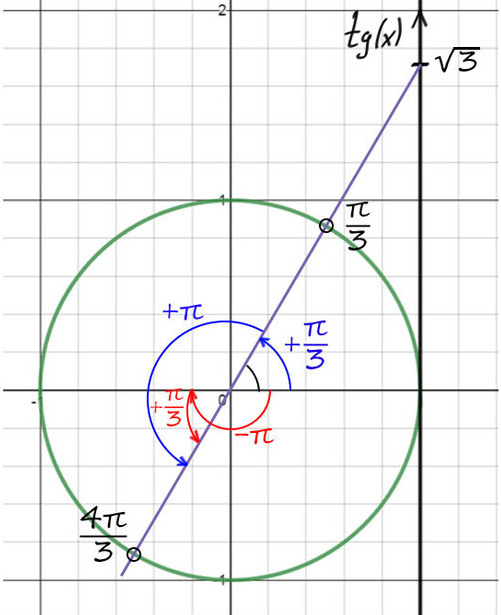
2) Проведем фиолетовую прямую через значение √3 и начало координат. Опять на пересечении с окружностью получается 2 точки.

По мнемоническому правилу при тангенсе √3 первое значение — это π/3.

3) Чтобы попасть во вторую точку, можно к первой точке (π/3) прибавить π => y = π/3 + π = 4π/3.

4) Но мы нашли только y , вернемся к х. y = π/3 + 2πn и y = x + π/4, тогда x + π/4 = π/3 + 2πn => x = π/12 + 2πn, n∈Ζ.

Второй корень: y = 4π/3 + 2πk и y = x + π/4, тогда x + π/4 = 4π/3 + 2πk => x = 13π/12 + 2πk, k∈Ζ.

Теперь корни на окружности будут здесь:

Ответ: π/12 + 2πn и 13π/12 + 2πk, k и n — любые целые числа.

Конечно, эти два ответа можно объединить в один. От 0 поворот на π/12, а дальше каждый корень будет повторяться через каждый π (180°).

Ответ можно записать и так: π/12 + πn, n∈Ζ.

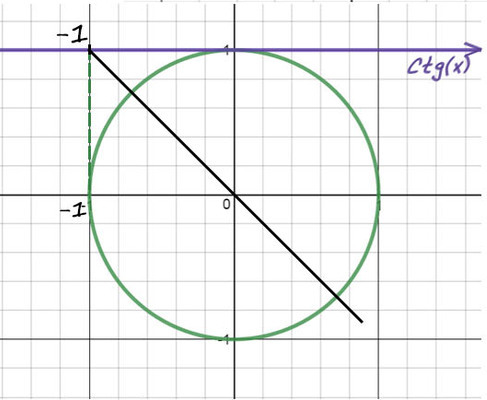
Пример №4: −10ctg(x) = 10

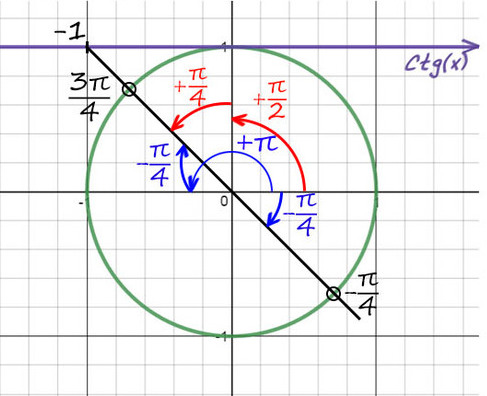
Перенесем (−10) в другую часть: ctg(x) = −1. Отметим значение -1 на оси котангенсов.

1) Проведем прямую через эту точку и начало координат.

2) Придется опять вспомнить, когда деление косинуса на синус даст еденицу (это получается при π/4). Но здесь −1, поэтому одна точка будет −π/4. А вторую найдем поворотом до π, а потом назад на π/4 (π − π/4).

Можно это сделать по-другому (красным цветом), но мой вам совет: всегда отсчитывайте от целых значений пи (π, 2π, 3π. ) так намного меньше шансов запутаться.

Не забываем добавить к каждой точке 2πk.

Ответ: 3π/4 + 2πn и −π/4 + 2πk, k и n — любые целые числа.

Алгоритм решения тригонометрических уравнений (на примере cos(x) = − √ 3/2) :

1. Отмечаем значение (−√3/2) на оси тригонометрической функции (косинусов, это ось Х).
2. Проводим перпендикулярную прямую оси (косинусов) до пересечений с окружностью.
3. Точки пересечения с окружностью и будут являться корнями уравнения.
4. Значение одной точки (без разницы, как в нее попадете) +2πk.

Азов достаточно, прежде чем идти дальше закрепите полученные знания.

Видео:Алгебра 10 класс. 20 сентября. Числовая окружность #6 координаты точекСкачать

Всё про окружность и круг

Окружность — это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.

Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.

Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.

Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2

Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.

Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.

Квадрат касательной равен произведению секущей на ее внешнюю часть

Центральный угол — это угол, вершина которого совпадает с центром окружности.

Дугой называется часть окружности, заключенная между двумя точками.

Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.

Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.

Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.

Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.

Периметр сектора: P = s + 2R.

Площадь сектора: S = Rs/2 = ПR 2 а/360°.

Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.

Видео:Тригонометрическая окружность. Как выучить?Скачать

Окружность

Привет, друг! Ниже собрана вся информация по окружности: что это такое, как найти ее величины, как круг связан с тригонометрией. Это поможет тебе еще лучше разобраться с этими темами, а также верно решать задачи! Время прочтения — 10 минут.

Видео:Coordinates on Circle - Координаты точек окружностиСкачать

Что такое окружность?

Окружность — это множество всех точек на плоскости, находящихся на одинаковом расстоянии от данной точки, а ее радиусом называют отрезок, который соединяет любую её точку с центром (все радиусы окружности равны). У окружности также есть диаметр — отрезок, соединяющий две точки окружности и проходящий через её центр.

Выделяют также такое понятие как единичная окружность. Она представляет из себя такую окружность, центр которой располагается в начале координат, а ее радиус равен единице.

Есть еще один вид окружности — числовая. Это обычная единичная окружность, но с уже установленным соответствием между действительными числами и точками.

Видео:Как найти координаты точек на тригонометрической окружностиСкачать

Как найти длину окружности

Зачастую в задачах просят найти длину окружности, как это сделать?

Так, для того чтобы найти длину окружности, нужно:

1. Диаметр этой окружности умножить на , число ≈ 3,1415926535…

1. Найти удвоенное произведение радиуса и числа

Видео:Как проверяют учеников перед ЕНТСкачать

Формулы:

Где r — это радиус окружности, а d — ее диаметр, а число — это математическая константа (отношение длины окружности к длине ее диаметра)

Чему равен радиус окружности

Радиус окружности необходимо знать, чтобы решить многие задачи, поэтому давай вместе разберем, как его можно найти.

1. Через площадь окружности : R=s, где S — площадь круга, — это математическая константа, которая объяснена выше.
2. Через длину круга: R=P2, где P — длина круга.
3. Через диаметр окружности: R=d2, где d — диаметр.
4. Через диагональ вписанного треугольника: R=d2, где d=a2 b2.
5. Через сторону описанного квадрата: R= a2, где а — сторона описанного квадрата.
6. Через стороны и площадь вписанного треугольника: R=abc4S, где abc — стороны вписанного треугольника, а S — его площадь.
7. Через площадь и полупериметр описанного треугольника: R=sp, где S — площадь треугольника, а p — полупериметр.
8. Через площадь сектора и его центральный угол: R=360Spa, где S — площадь сектора круга, α — его центральный угол.
9. Через сторону вписанного правильного многоугольника: R=a2sin(180N), где a — сторона правильного многоугольника (все его стороны равны), N — количество сторон многоугольника.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Окружность в тригонометрии

Окружность используется и в тригонометрии:

Что значат на рисунке все обозначение?

1. Присутствует перевод градусов в радианы (и наоборот). В полном круге — 360 градусов ( радиан);

1. Значение косинуса угла — на оси Х, а значение синуса — на У;

1. Синус и косинус имеют значения от -1 до 1;

1. На тригонометрическом круге видно, что косинус как и синус — периодические (один период равен 2).

Видео:Алгебра 10 класс Поворот точки вокруг начала координат ЛекцияСкачать

Что еще важно знать?

Полный круг — 360 градусов.

Точка с координатами (1;0) — угол 0 градусов соответствует углу ноль градусов, а точка с координатами (-1;0) соответствует углу 180 градусов, точка с координатами (0;1) — в 90 градусов.

Косинус угла — абсцисса точки на единичной окружности, которая соответствует приведенному углу.

Синус угла — ордината точки на единичной окружности, которая соответствует приведенному углу.

Потому как окружность единичная, то для любого угла и синус, и косинус находятся в пределах от -1 до 1. Так:

Из этого можно выделить основное тригонометрическое тождество:

cos^2 a + sin^2 a = 1

По рисунку видно, что

,

Углы могут быть и больше 360 градусов. Например, угол 720 — это два полных оборота по часовой стрелке. Из этого можно сделать такой вывод:

Если же применять в этих формулах не градусы, а радианы, то:

Можно также по рисунку тригонометрической окружности определить тангенс угла и котангенс:

В результате, мы получаем таблицу:

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Углы поворота

Угол поворота — это угол, образованный положительным направлением оси OX и лучом OA.

Их величина не имеет зависимости от радиуса приведенной окружности.

Угол в первом квадранте(четверти круга), имеет все положительные значения тригонометрических функций.

Во втором квадранте все функции (кроме sin и cos) — отрицательные.

В третьем квадранте значения всех функций (помимо tg и ctg) меньше 0.

В четвертом квадранте все функции (кроме cos и sec) с отрицательным значением.

Видео:Точки на числовой окружностиСкачать

Числовая окружность

В этой статье мы очень подробно разберем определение числовой окружности, узнаем её главное свойство и расставим числа 1,2,3 и т.д. Про то, как отмечать другие числа на окружности (например, (frac, frac, frac, 10π, -frac)) разбирается в этой статье .

Числовой окружностью называют окружность единичного радиуса, точки которой соответствуют действительным числам , расставленным по следующим правилам:

1) Начало отсчета находится в крайней правой точке окружности;

2) Против часовой стрелки — положительное направление; по часовой – отрицательное;

3) Если в положительном направлении отложить на окружности расстояние (t), то мы попадем в точку со значением (t);

4) Если в отрицательном направлении отложить на окружности расстояние (t), то мы попадем в точку со значением (–t).

Почему окружность называется числовой?
Потому что на ней обозначаются числа. В этом окружность похожа на числовую ось – на окружности, как и на оси, для каждого числа есть определенная точка.

Зачем знать, что такое числовая окружность?
С помощью числовой окружности определяют значение синусов, косинусов, тангенсов и котангенсов. Поэтому для знания тригонометрии и сдачи ЕГЭ на 60+ баллов, обязательно нужно понимать, что такое числовая окружность и как на ней расставить точки.

Что в определении означают слова «…единичного радиуса…»?
Это значит, что радиус этой окружности равен (1). И если мы построим такую окружность с центром в начале координат, то она будет пересекаться с осями в точках (1) и (-1).

Ее не обязательно рисовать маленькой, можно изменить «размер» делений по осям, тогда картинка будет крупнее (см. ниже).

Почему радиус именно единица? Так удобнее, ведь в этом случае при вычислении длины окружности с помощью формулы (l=2πR) мы получим:

Длина числовой окружности равна (2π) или примерно (6,28).

А что значит «…точки которой соответствуют действительным числам»?
Как говорили выше, на числовой окружности для любого действительного числа обязательно найдется его «место» — точка, которая соответствует этому числу.

Зачем определять на числовой окружности начало отсчета и направления?
Главная цель числовой окружности — каждому числу однозначно определить свою точку. Но как можно определить, где поставить точку, если неизвестно откуда считать и куда двигаться?

Тут важно не путать начало отсчета на координатной прямой и на числовой окружности – это две разные системы отсчета! А так же не путайте (1) на оси (x) и (0) на окружности – это точки на разных объектах.

Видео:7 Точки с целыми координатами и диагональ квадратаСкачать

Какие точки соответствуют числам (1), (2) и т.д?

Помните, мы приняли, что у числовой окружности радиус равен (1)? Это и будет нашим единичным отрезком (по аналогии с числовой осью), который мы будем откладывать на окружности.

Чтобы отметить на числовой окружности точку соответствующую числу 1, нужно от 0 пройти расстояние равное радиусу в положительном направлении.

Чтобы отметить на окружности точку соответствующую числу (2), нужно пройти расстояние равное двум радиусам от начала отсчета, чтобы (3) – расстояние равное трем радиусам и т.д.

При взгляде на эту картинку у вас могут возникнуть 2 вопроса:
1. Что будет, когда окружность «закончится» (т.е. мы сделаем полный оборот)?
Ответ: пойдем на второй круг! А когда и второй закончится, пойдем на третий и так далее. Поэтому на окружность можно нанести бесконечное количество чисел.

2. Где будут отрицательные числа?
Ответ: там же! Их можно так же расставить, отсчитывая от нуля нужное количество радиусов, но теперь в отрицательном направлении.

К сожалению, обозначать на числовой окружности целые числа затруднительно. Это связано с тем, что длина числовой окружности будет равна не целому числу: (2π). И на самых удобных местах (в точках пересечения с осями) тоже будут не целые числа, а доли числа (π) : ( frac),(-frac),(frac), (2π). Поэтому при работе с окружностью чаще используют числа с (π). Обозначать такие числа гораздо проще (как это делается можете прочитать в этой статье ).

Видео:Координаты точек на числовой окружности, часть 5. Алгебра 10 класс.Скачать

Главное свойство числовой окружности

Одному числу на числовой окружности соответствует одна точка, но одной точке соответствует множество чисел.

Такая вот математическая полигамия.

И следствие из этого правила:

Все значения одной точки на числовой окружности можно записать с помощью формулы:

Если хотите узнать логику этой формулы, и зачем она нужна, посмотрите это видео .

В данной статье мы рассмотрели только теорию о числовой окружности, о том как расставляются точки на числовой и окружности и принципе, как с ней работать вы можете прочитать здесь .

Что надо запомнить про числовую окружность:

💡 Видео

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

10 класс, 12 урок, Числовая окружность на координатной плоскостиСкачать

Радианная мера угла. 9 класс.Скачать

Расчет угловых координат с окружности 👍Скачать

Математика это не ИсламСкачать