Центром тяжести (или центром масс) некоторого тела называется точка, обладающая тем свойством, что если подвесить тело за эту точку, то оно будет сохранять свое положение.
Ниже рассмотрены двумерные и трёхмерные задачи, связанные с поиском различных центров масс — в основном с точки зрения вычислительной геометрии.
В рассмотренных ниже решениях можно выделить два основных факта. Первый — что центр масс системы материальных точек равен среднему их координат, взятых с коэффициентами, пропорциональными их массам. Второй факт — что если мы знаем центры масс двух непересекающихся фигур, то центр масс их объединения будет лежать на отрезке, соединяющем эти два центра, причём он будет делить его в то же отношении, как масса второй фигуры относится к массе первой.
- Двумерный случай: многоугольники
- Центр масс системы точек
- Центр масс каркаса
- Центр масс сплошной фигуры
- Случай треугольника
- Случай треугольника: доказательство
- Случай многоугольника
- Случай многоугольника: альтернативный способ
- Трёхмерный случай: многогранники
- Центр масс системы точек
- Центр масс каркаса многогранника
- Центр масс поверхности многогранника
- Центр масс сплошного многогранника
- Случай тетраэдра
- Случай произвольного многогранника
- Please wait.
- We are checking your browser. mathvox.ru
- Why do I have to complete a CAPTCHA?
- What can I do to prevent this in the future?
- Методическая разработка урока «Замечательные точки треугольника (центр тяжести)»
- Ход урока
- I. Самоопределение к учебной деятельности.
- II. Актуализация знаний и фиксация затруднения в деятельности.
- III. Выявление причины затруднения и постановка цели деятельности.
- IV. Построение проекта выхода из затруднения.
- V. Первичное закрепление.
- VI. Рефлексия учебной деятельности на уроке.
- 📸 Видео
Видео:Механика | динамика | центр масс треугольникаСкачать

Двумерный случай: многоугольники
На самом деле, говоря о центре масс двумерной фигуры, можно иметь в виду одну из трёх следующих задач:
- Центр масс системы точек — т.е. вся масса сосредоточена только в вершинах многоугольника.
- Центр масс каркаса — т.е. масса многоугольника сосредоточена на его периметре.
- Центр масс сплошной фигуры — т.е. масса многоугольника распределена по всей его площади.
Каждая из этих задач имеет самостоятельное решение, и будет рассмотрена ниже отдельно.
Центр масс системы точек
Это самая простая из трёх задач, и её решение — известная физическая формула центра масс системы материальных точек:
где 


В частности, если все точки имеют одинаковую массу, то координаты центра масс есть среднее арифметическое координат точек. Для треугольника эта точка называется центроидом и совпадает с точкой пересечения медиан:
Для доказательства этих формул достаточно вспомнить, что равновесие достигается в такой точке 

и, выражая отсюда 
Центр масс каркаса
Будем считать для простоты, что каркас однороден, т.е. его плотность везде одна и та же.
Но тогда каждую сторону многоугольника можно заменить одной точкой — серединой этого отрезка (т.к. центр масс однородного отрезка есть середина этого отрезка), с массой, равной длине этого отрезка.
Теперь мы получили задачу о системе материальных точек, и применяя к ней решение из предыдущего пункта, мы находим:
где 




Для треугольника можно показать следующее утверждение: эта точка является точкой пересечения биссектрис треугольника, образованного серединами сторон исходного треугольника. (чтобы показать это, надо воспользоваться приведённой выше формулой, и затем заметить, что биссектрисы делят стороны получившегося треугольника в тех же соотношениях, что и центры масс этих сторон).
Центр масс сплошной фигуры
Мы считаем, что масса распределена по фигуре однородно, т.е. плотность в каждой точке фигуры равна одному и тому же числу.
Случай треугольника
Утверждается, что для треугольника ответом будет всё тот же центроид, т.е. точка, образованная средним арифметическим координат вершин:
Случай треугольника: доказательство
Приведём здесь элементарное доказательство, не использующее теорию интегралов.
Первым подобное, чисто геометрическое, доказательство привёл Архимед, но оно было весьма сложным, с большим числом геометрических построений. Приведённое здесь доказательство взято из статьи Apostol, Mnatsakanian «Finding Centroids the Easy Way».
Доказательство сводится к тому, чтобы показать, что центр масс треугольника лежит на одной из медиан; повторяя этот процесс ещё дважды, мы тем самым покажем, что центр масс лежит в точке пересечения медиан, которая и есть центроид.
Разобьём данный треугольник 
Четыре получившихся треугольника подобны треугольнику 

Треугольники №1 и №2 вместе образуют параллелограмм, центр масс которого 


Пусть теперь вектор 





Наша цель — показать, что вектора 

Обозначим через 






Искомый центр масс 




Таким образом, вектор от вершины 





Таким образом, мы доказали, что вектора 



Более того, попутно мы доказали, что центроид делит каждую медиану в отношении 
Случай многоугольника
Перейдём теперь к общему случаю — т.е. к случаю мноугоугольника. Для него такие рассуждения уже неприменимы, поэтому сведём задачу к треугольной: а именно, разобьём многоугольник на треугольники (т.е. триангулируем его), найдём центр масс каждого треугольника, а затем найдём центр масс получившихся центров масс треугольников.
Окончательная формула получается следующей:
где 



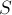
Триангуляция выпуклого многоугольника — тривиальная задача: для этого, например, можно взять треугольники 

Случай многоугольника: альтернативный способ
С другой стороны, применение приведённой формулы не очень удобно для невыпуклых многоугольников, поскольку произвести их триангуляцию — сама по себе непростая задача. Но для таких многоугольников можно придумать более простой подход. А именно, проведём аналогию с тем, как можно искать площадь произвольного многоугольника: выбирается произвольная точка 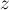


где 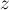



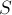

Видео:97 Медианы и центр тяжести треугольникаСкачать

Трёхмерный случай: многогранники
Аналогично двумерному случаю, в 3D можно говорить сразу о четырёх возможных постановках задачи:
- Центр масс системы точек — вершин многогранника.
- Центр масс каркаса — рёбер многогранника.
- Центр масс поверхности — т.е. масса распределена по площади поверхности многогранника.
- Центр масс сплошного многогранника — т.е. масса распределена по всему многограннику.
Центр масс системы точек
Как и в двумерном случае, мы можем применить физическую формулу и получить тот же самый результат:
который в случае равных масс превращается в среднее арифметическое координат всех точек.
Центр масс каркаса многогранника
Аналогично двумерному случаю, мы просто заменяем каждое ребро многогранника материальной точкой, расположенной посередине этого ребра, и с массой, равной длине этого ребра. Получив задачу о материальных точках, мы легко находим её решение как взвешенную сумму координат этих точек.
Центр масс поверхности многогранника
Каждая грань поверхности многогранника — двухмерная фигура, центр масс которой мы умеем искать. Найдя эти центры масс и заменив каждую грань её центром масс, мы получим задачу с материальными точками, которую уже легко решить.
Центр масс сплошного многогранника
Случай тетраэдра
Как и в двумерном случае, решим сначала простейшую задачу — задачу для тетраэдра.
Утверждается, что центр масс тетраэдра совпадает с точкой пересечения его медиан (медианой тетраэдра называется отрезок, проведённый из его вершины в центр масс противоположной грани; таким образом, медиана тетраэдра проходит через вершину и через точку пересечения медиан треугольной грани).
Почему это так? Здесь верны рассуждения, аналогичные двумерному случаю: если мы рассечём тетраэдр на два тетраэдра с помощью плоскости, проходящей через вершину тетраэдра и какую-нибудь медиану противоположной грани, то оба получившихся тетраэдра будут иметь одинаковый объём (т.к. треугольная грань разобьётся медианой на два треугольника равной площади, а высота двух тетраэдров не изменится). Повторяя эти рассуждения несколько раз, получаем, что центр масс лежит на точке пересечения медиан тетраэдра.
Эта точка — точка пересечения медиан тетраэдра — называется его центроидом. Можно показать, что она на самом деле имеет координаты, равные среднему арифметическому координат вершин тетраэдра:
(это можно вывести из того факта, что центроид делит медианы в отношении 
Таким образом, между случаями тетраэдра и треугольника принципиальной разницы нет: точка, равная среднему арифметическому вершин, является центром масс сразу в двух постановках задачи: и когда массы находится только в вершинах, и когда массы распределены по всей площади/объёму. На самом деле, этот результат обобщается на произвольную размерность: центр масс произвольного симплекса (simplex) есть среднее арифметическое координат его вершин.
Случай произвольного многогранника
Перейдём теперь к общему случаю — случаю произвольного многогранника.
Снова, как и в двумерном случае, мы производим сведение этой задачи к уже решённой: разбиваем многогранник на тетраэдры (т.е. производим его тетраэдризацию), находим центр масс каждого из них, и получаем окончательный ответ на задачу в виде взвешенной суммы найденных центров масс.
Видео:Центр тяжести треугольникаСкачать

Please wait.
Видео:координаты центра тяжести треугольникаСкачать

We are checking your browser. mathvox.ru
Видео:8. Медиана треугольника и её свойства.Скачать

Why do I have to complete a CAPTCHA?
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
Видео:Урок 79. Центр масс тела и методы определения его положенияСкачать

What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.
Cloudflare Ray ID: 6d804a453ef10056 • Your IP : 85.95.188.35 • Performance & security by Cloudflare
Видео:Центр тяжестиСкачать

Методическая разработка урока «Замечательные точки треугольника (центр тяжести)»
Разделы: Математика
Тип урока: урок «открытия» нового знания.
Программа: «Школа 2000…».
Учебник: «Математика, 6 класс, часть 3».
Авторы: Дорофеев Георгий Владимирович, Петерсон Людмила Георгиевна.
Цели урока:
- Дидактическая: ввести понятие замечательной точки треугольника – центра тяжести; способствовать выработке навыков построения центра тяжести.
- Развивающая: способствовать развитию мыслительной деятельности учащихся, развитию математической речи; умение слушать другого и понимать его речь.
- Воспитательная: воспитывать аккуратность выполнения заданий, формировать любознательность, пробуждать интерес ко всему, что нас окружает.
Формы работы: фронтальная, индивидуальная.
Видео:Почему точка пересечения медиан называется центром масс?Скачать

Ход урока
I. Самоопределение к учебной деятельности.
Цели этапа:
- включить учащихся в учебную деятельность;
- определить содержательные рамки урока – продолжаем изучать геометрические фигуры.
| Деятельность учителя | Предполагаемые ответы учащихся |
| Здравствуйте, ребята! Я вижу, что у вас хорошее настроение, надеюсь оно останется в течение всей работы. Вспомните, какой раздел математики мы изучаем? Что изучает геометрия? Чему вы научились на предыдущих уроках? Какие виды треугольников вы знаете? А как думаете, все уже узнали про треугольники? Итак, продолжим изучать замечательную науку – геометрию. |
II. Актуализация знаний и фиксация затруднения в деятельности.
Цели этапа:
- актуализировать учебное содержание необходимое и достаточное для изучения нового материала: работа с треугольником, его элементами;
- актуализировать мыслительные операции: анализ, сравнение, обобщение.
| Деятельность учителя | Предполагаемые ответы учащихся |
| Посмотрите на рисунок. Какие геометрические фигуры вы видите, назовите их.  Вспомните, что такое биссектриса угла? (на доску вывешивается табличка с определением) Как ее можно построить? Сколько биссектрис в треугольнике можно провести? Что такое медиана треугольника? Как ее можно построить? Сколько медиан в треугольнике можно провести? Я вам предлагаю построить с помощью линейки и транспортира медианы и биссектрисы треугольника. | Треугольник АВД. Медиана АЕ. Биссектриса ВК. Биссектриса угла – это луч, исходящий из вершины угла и делящий его пополам. С помощью транспортира измерить угол, поделить градусную меру пополам, провести луч. Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. С помощью линейки построить середину стороны и полученную точку соединить с противоположной вершиной треугольника. (каждый учащийся строит медианы и биссектрисы своего треугольника) |
III. Выявление причины затруднения и постановка цели деятельности.
Цели этапа:
- организовать коммуникативное взаимодействие, в ходе которого выявляется и фиксируется отличительное свойство задания, вызвавшего затруднение в учебной деятельности;
- согласовать цель и тему урока.
| Деятельность учителя | Предполагаемые ответы учащихся |
| Что можете заметить (если точно выполнили построение)? У всех получилось? А сейчас я проведу эксперимент. Почему у вас не получилось с первого раза установить треугольник? Какова цель урока? Сформулируйте тему урока. Вы назвали интересные варианты. Предлагаю пока остановиться на такой теме: «Интересные точки треугольника» (тема записывается на доске). | Медианы пересеклись в одной точке и биссектрисы пересеклись в одной точке. (учащиеся пытаются установить треугольник на стержень) Не знаем, в каком месте треугольника надо подставить стержень. Выяснить, в какую точку треугольника надо поставить стержень, чтобы треугольник находился в равновесии. (учащиеся предлагают варианты темы урока) |
IV. Построение проекта выхода из затруднения.
Цели этапа:
- организовать коммуникативное взаимодействие для построения нового способа действия, устраняющего причину выявленного затруднения;
- зафиксировать новый способ действия.
| Деятельность учителя | Предполагаемые ответы учащихся |
| Какие точки вы построили на ваших треугольниках? Попробуйте с ними поэкспериментировать. Итак, я смотрю, что у многих получилось установить треугольник в равновесии на стержень. Как бы вы назвали эту точку? В математике эту точку назвали центром тяжести. Это одна из замечательных точек треугольника. Какая точка всем помогла? Давайте уточним тему урока. | Точки пересечения медиан и биссектрис. (учащиеся пытаются установить треугольник в равновесие на стержень) Точка пересечения медиан Точка пересечения медиан или биссектрис (у 3 группы, где были выданы равносторонние треугольники). (учащиеся предлагают свои варианты) Необходимо было выяснить, в какую точку треугольника надо поставить стержень, чтобы треугольник находился в равновесии. Точка пересечения медиан. Центром тяжести, замечательной точкой треугольника. Построить медианы треугольника. Замечательная точка треугольника – центр тяжести. |
V. Первичное закрепление.
Цель этапа:
- зафиксировать изученное учебное содержание.
| Деятельность учителя | Предполагаемые ответы учащихся |
| А для всех видов треугольников центром тяжести будет точка пересечения медиан? У вас на столах лежат еще тупоугольные треугольники. Постройте центр тяжести и проведите эксперимент. Получилось? | Наверное. (учащиеся работают с тупоугольными треугольниками) Две, так как они пересекутся в одной точке. |
VI. Рефлексия учебной деятельности на уроке.
Цели этапа:
- зафиксировать новое содержание, изученное на уроке;
- оценить собственную деятельность на уроке;
- зафиксировать затруднения как направления будущей учебной деятельности;
- обсудить и записать домашнее задание.
| Деятельность учителя | Предполагаемые ответы учащихся |
| Что нового узнали на уроке? Любой треугольник имеет центр тяжести? Какие трудности испытывали во время выполнения работы? Где в жизни встречали сегодняшнее открытие? А есть еще замечательные точки у треугольника? Об этом мы узнаем на следующих уроках. Запишите домашнее задание: Все молодцы. Спасибо за урок. До свидания. | У треугольника есть замечательная точка – центр тяжести. Чтобы его найти, надо построить хотя бы две медианы. С помощью этой точки можно треугольник установить в равновесии на палочке. (выслушать ответы учащихся) (учащиеся называют примеры из жизни) 📸 ВидеоМетод центра масс. Олимпиадная математика. Be Student SchoolСкачать  Найдите центр тяжестиСкачать  Три центра массСкачать  Галилео. Эксперимент. Центр массСкачать  Центр масс (определение и базовые свойства)Скачать  Теорема о точке пересечения медиан треугольника. Доказательство. 8 класс.Скачать  Центр массСкачать  Определение центра тяжести сложной фигуры. СопроматСкачать  Урок 80. Определение положения центра масс телаСкачать  Центр масс в математике (или механика помогает геометрии)Скачать  3.3. Центр масс и закон его движения | Динамика | Александр Чирцов | ЛекториумСкачать  Видеоурок 3. Определение центра тяжести.Скачать  |












