- «Календарь счастливой жизни: инструменты и механизм работы для достижения своих целей»
- «Управление общеобразовательной организацией: новые тенденции и современные технологии»
- Дистанционное обучение как современный формат преподавания
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Математика: теория и методика преподавания в образовательной организации
- Оставьте свой комментарий
- Подарочные сертификаты
- Геометрия 10 класс. Тематические тесты тест по геометрии (10 класс) на тему
- Скачать:
- Предварительный просмотр:
- Предварительный просмотр:
- Узнать ещё
- Сечение куба плоскостью
- 🔍 Видео
Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»
Сертификат и скидка на обучение каждому участнику
Видео:Геометрия 10 класс (Урок№6 - Параллельность плоскостей.)Скачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Геометрический диктант Параллельные прямые в пространстве. Параллельность трех прямых Параллельность прямой и плоскости
Задание 1 Дан параллелепипед. Параллельны ли прямые СК и DA1? Выберите один из 3 вариантов ответа: 1) нет 2) да 3) зависит от размеров параллелепипеда
Задание 2 Если в пространстве даны две параллельные прямые и третья прямая пересекает одну из параллельных, то пересекает ли она вторую из параллельных прямых? Выберите один из 2 вариантов ответа: 1) не обязательно 2) обязательно пересекает
Задание 3 Сколько прямых, параллельных данной прямой, можно провести в пространстве через точку, не принадлежащую этой прямой? (в ответе укажите только число) Запишите число: ___________________________
Задание 4 В основании прямоугольного параллелепипеда ABCDA1B1C1D1 лежит квадрат со стороной 1 см, а длина бокового ребра параллелепипеда равна 3 см. Точки P, T, O и K являются серединами отрезков AB, BB1, B1D и AD соответственно. Вычислите периметр четырехугольника PTOK. Выберите один из 5 вариантов ответа:
Задание 5 ABCDA1B1C1D1 — параллелепипед. Сколько прямых, параллельных прямой DC, можно назвать на рисунке. В ответе укажите только число. Запишите число: ___________________________
Задание 6 Если в пространстве даны две параллельные прямые и одна из них пересекает некоторую плоскость, то пересекает ли эту плоскость другая параллельная прямая? Выберите один из 3 вариантов ответа: 1) нет 2) не обязательно 3) да
Задание 7 Если взять ребро куба, то сколько других ребер ему параллельны? (в ответе укажите только число) Запишите число: ___________________________
Задание 8 Сколько существует вариантов взаимного расположения двух различных прямых в пространстве? Выберите один из 3 вариантов ответа: 1) 1 2) 2 3) 3
Задание 9 Дан куб. Какие из указанных ниже пар ребер — параллельны?
Задание 10 Дан параллелепипед. Параллельны ли прямые АК и DM? Выберите один из 3 вариантов ответа: 1) да 2) зависит от размеров параллелепипеда 3) нет
Задание 11 Укажите верное утверждение. Прямая CМ: Выберите один из 4 вариантов ответа: 1) пересекает плоскость АВА1 2) параллельна прямой ВN 3) пересекает плоскость АА1D1 4) параллельна плоскости АА1В1
Задание 12 Дано: АВ параллельно плоскости α, AD параллельно BC. Найти: угол ADC. (в ответе укажите только число, например, 90) Запишите число: ___________________________
Задание 13 Если в пространстве даны две параллельные прямые, плоскость, в которой они не лежат, и одна из прямых параллельна плоскости, то параллельна ли плоскости другая прямая? Выберите один из 3 вариантов ответа: 1) не всегда 2) нет 3) да
Задание 14 Если прямая не имеет с плоскостью общих точек, то как относительно плоскости расположена эта прямая? Выберите один из 3 вариантов ответа: 1) параллельно 2) лежит в плоскости 3) пересекает
Задание 15 Дано: АВ параллельно плоскости α, АВ = 17, МК = 21. Найти: DC. Выберите один из 5 вариантов ответа: 1) 23 2) 40 3) 34 4) 17 5) 25
Задание 16 Сколько плоскостей, заданных вершинами куба, параллельны прямой CD? (в ответе укажите только число) Запишите число: ___________________________
Задание 17 Сколько прямых, заданных вершинами прямоугольного параллелепипеда, параллельны плоскости A1DC? (в ответе укажите только число) Запишите число: ___________________________
Задание 18 Укажите верное утверждение. Прямая СN: Выберите один из 4 вариантов ответа: 1) пересекает плоскость АА1В 2) параллельна плоскости ADM 3) параллельна прямой DM 4) параллельна плоскости АА1В1
Задание 19 Сколько прямых, параллельных данной плоскости, можно провести в пространстве через точку, не принадлежащую этой плоскости? (в ответе укажите только число) Выберите один из 5 вариантов ответа: 1) 10 2) 2 3) 3 4) 1 5) бесконечно много
Задание 20 Сколько существует вариантов взаимного расположения прямой и плоскости в пространстве? Выберите один из 3 вариантов ответа: 1) 2 2) 3 3) 1
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 966 человек из 79 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 342 человека из 71 региона
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 688 человек из 74 регионов
Ищем педагогов в команду «Инфоурок»
- БРОДОВСКАЯ ТАМАРА АЛЕКСАНДРОВНАНаписать 6954 17.12.2018
Номер материала: ДБ-309659
- 13.12.2018 134
- 11.12.2018 99
- 11.12.2018 4564
- 11.12.2018 3903
- 09.12.2018 576
- 09.12.2018 189
- 09.12.2018 828
- 08.12.2018 195
Не нашли то, что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Минпросвещения рассказали о формате обучения школьников после праздников
Время чтения: 1 минута
В Госдуме предложили продлить каникулы для школьников до 16 января
Время чтения: 1 минута
В России разработают рекомендации по сопровождению студентов с ОВЗ
Время чтения: 2 минуты
Правительство направит регионам почти 92 миллиарда рублей на ремонт и оснащение школ
Время чтения: 1 минута
Россия направит $10,3 млн на развитие школьного питания в нескольких странах
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Геометрия 10 класс. Тематические тесты
тест по геометрии (10 класс) на тему
Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Скачать:
| Вложение | Размер |
|---|---|
| test_1._aksiomy_stereometrii.doc | 143 КБ |
| test_2._parallelnost_pryamykh_i_ploskostey.doc | 354.5 КБ |
| test_3._perpendikulyarnost_pryamykh_i_ploskostey.doc | 130 КБ |
| test_4._mnogogranniki.doc | 53.5 КБ |
| test_5._vektory_v_prostranstve.doc | 89.5 КБ |
| otvety.doc | 43 КБ |
Бесплатный марафон подготовки к ЕГЭ на зимних каникулах
Учи.Дома запускает бесплатный марафон в котором каждый день. В течении 5 дней утром ты будешь получать одно задание по выбранному предмету, а вечером его решение. Твоя задача, успеть выполнение задание до того как получишь ответ.
Бесплатно, онлайн, подготовка к ЕГЭ
Видео:10 класс, 10 урок, Параллельные плоскостиСкачать

Предварительный просмотр:
Точка Р лежит на прямой МN. Назовите плоскость, которой принадлежит точка Р.
1) АВС 2) DBC 3) DAB 4) DAC
Каким плоскост ям принадлежит точка К?
Выберите верные высказывания:
1) Любые три точки лежат в одной плоскости.
2) Если центр окружности и ее точка лежат в плоскости, то и вся окружность лежит в этой плоскости.
3) Через три точки, лежащих на прямой, проходит только одна плоскость.
4) Через две пересекающихся прямые проходит плоскость , и притом только одна.
Выберите неверные высказывания:
1) Если три прямые имеют общую точку, то они лежат в одной плоскости.
2) Прямая, пересекающая две стороны треугольника, лежит в плоскости этого треугольника.
3) Две плоскости могут имеет только две общие точки.
4) Три попарно пересекающиеся в разных точках прямые, лежат в одной плоскости.
Назовите прямую, по которой пересекаются плоскости A 1 BC и A 1 AD.
3) D 1 D 4) D 1 C
Назовите прямую, по которой пересекаются плоскости DCC 1 и A 1 AD.
3) D 1 D 4) D 1 C
Прямые АВ и CD пересекаются. Через прямую АВ проведена плоскость. Назовите линию пересечения данной плоскости с плоскостью ВСD.
1) АС 2) АB 3) BС 4) ВD
Прямые АВ и CD пересекаются. Через точки В и D проведена плоскость. Назовите линию пересечения данной плоскости с плоскостью AСD.
1) АС 2) АB 3) BС 4) ВD
Точка Р лежит на прямой МN. Назовите плоскость, которой принадлежит точка Р.
1) АВС 2) DBC 3) DAB 4) DAC
Каким плоскостям принадлежит точка F?
Выберите верные высказывания:
1) Любые четыре точки лежат в одной плоскости.
2) Через прямую и не лежащую на ней точку проходит только одна плоскость.
3) Если три точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости .
4) Две плоскости могут иметь только одну общую точку.
Выберите неверные высказывания:
1) Две окружности, имеющие общий центр, лежат в одной плоскости .
2) Прямая, проходящая через вершину треугольника, лежит в плоскости этого треугольника.
3) Три вершины треугольника принадлежат одной плоскости.
4) Через две параллельные прямые проходит плоскость , и притом только одна.
Назовите прямую, по которой пересекаются плоскости DCC 1 и A 1 BC.
3) D 1 D 4) D 1 C
Назовите прямую, по которой пересекаются плоскости ABC и C 1 CB.
3) A 1 B 4) B 1 B
Прямые АВ и CD пересекаются. Через прямую CD проведена плоскость. Назовите линию пересечения данной плоскости с плоскостью AВС.
1) СD 2) АD 3) BС 4) ВD
Прямые АВ и CD пересекаются. Через точки A и D проведена плоскость. Назовите линию пересечения данной плоскости с плоскостью BСD.
1) АС 2) АD 3) BС 4) ВD
Видео:10. Параллельные плоскостиСкачать

Предварительный просмотр:
Параллельность прямых и плоскостей
Точки М, Р, К – середины ребер DA, DB, DC тетраэдра DABC. Назовите прямую, параллельную плоскости FBC.
1) МР 2) РК 3) МК 4) МК и РК
АВСDA 1 B 1 C 1 D 1 – прямоугольный параллелепипед. Какая из прямых параллельна плоскости A 1 B 1 C 1 ?
1) а 2) b 3) p 4) m
В тетраэдре DАВС ВК = КС, DP = PC. Плоскости какой грани параллельна прямая РК?
1) DAB 2) DBC 3) DAC 4) ABC
Выберите верные высказывания:
1) Две прямые в пространстве называются параллельными, если они не пересекаются.
2) Если одна из двух параллельных прямых параллельна плоскости, то другая прямая либо так же ей параллельна, либо лежит в этой плоскости.
3) Существует такая прямая, которая лежит в плоскости и параллельна прямой, пересекающей данную плоскость.
4) Скрещивающиеся прямые не имеют общих точек.
Точки А, В, С и D – середины ребер прямоугольного
параллелепипеда. Назовите параллельные прямые.
Точки А и D – середины ребер параллелепипеда. Выберите верные высказывания:
1) Прямые СD и MN скрещивающиеся.
2) Прямые АВ и MN лежат в одной плоскости.
3) Прямые СD и MN пересекаются.
4) Прямые АВ и СD скрещивающиеся.
Определите взаимное расположение прямых.
1) a и b – пересекающиеся прямые
2) a и b – параллельные прямые
3) a и b – скрещивающиеся прямые
Определите взаимное расположение прямых.
1) a и b – пересекающиеся прямые
2) a и b – параллельные прямые
3) a и b – скрещивающиеся прямые
Треугольники АВК и АВF расположены так, что прямые АВ и FK скрещиваются. Как расположены прямые АК и ВF?
1) они параллельны 2) скрещиваются 3) пересекаются
В тетраэдре DАВС АВ = ВС = АС = 20; DA = DB = DC = 40. Через середину ребра АС плоскость, параллельная АD и ВC. Найдите периметр сечения.
Параллельность прямых и плоскостей
Точки М, Р, К – середины ребер DA, DB, DC тетраэдра DABC. Назовите прямую, параллельную плоскости FАB.
1) МР 2) РК 3) МК 4) МК и РК
АВСDA 1 B 1 C 1 D 1 – прямоугольный параллелепипед. Какая из прямых параллельна плоскости A 1 AD?
1) а 2) b 3) p 4) m
В тетраэдре DАВС AM = MD, AN = NB. Плоскости какой грани параллельна прямая MN?
1) DAB 2) DBC 3) DAC 4) ABC
Выберите верные высказывания:
1) Параллельные прямые не имеют общих точек.
2) Если прямая параллельна данной плоскости, то она параллельна любой прямой, лежащей в этой плоскости.
3) Если прямая параллельна линии пересечения двух плоскостей и не принадлежит ни одной из них, то она параллельна каждой из этих плоскостей.
4) Существует параллелепипед, у которого все углы граней острые.
Точки А, В, С и D – середины ребер прямоугольного
параллелепипеда. Назовите параллельные прямые.
Точки А и D – середины ребер параллелепипеда. Выберите верные высказывания:
1) Прямые СD и MN пересекаются.
2) Прямые АВ и MN скрещивающиеся
3) Прямые АВ и СD параллельные.
4) Прямые АВ и MN пересекаются
Определите взаимное расположение прямых.
1) a и b – пересекающиеся прямые
2) a и b – параллельные прямые
3) a и b – скрещивающиеся прямые
Точки А и В – середины ребер параллелепипеда. Определите взаимное расположение прямых.
1) a и b – пересекающиеся прямые
2) a и b – параллельные прямые
3) a и b – скрещивающиеся прямые
Два равнобедренных треугольника АВС и АВD с общим основанием АВ расположены так, что точка С не лежит в плоскости АВD. Определите взаимное расположение прямых, содержащих медианы треугольников, проведенных к сторонам ВС и ВD.
1) они параллельны 2) скрещиваются 3) пересекаются
В тетраэдре DАВС АВ = ВС = АС = 10; DA = DB = DC = 20. Через середину ребра ВС плоскость, параллельная АС и ВD. Найдите периметр сечения.
Видео:Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Узнать ещё
Знание — сила. Познавательная информация
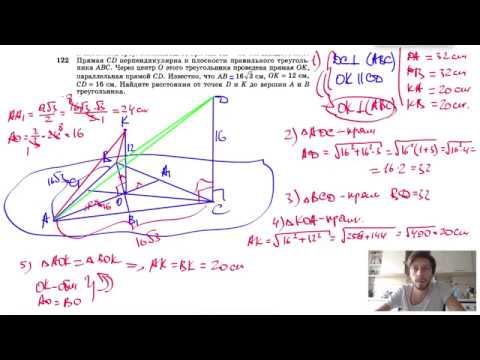
Видео:№122. Прямая CD перпендикулярна к плоскости правильного треугольника ABC. Через центр О этогоСкачать
Сечение куба плоскостью
Задачи на построение сечений куба плоскостью, как правило, проще чем, например, задачи на сечения пирамиды.
Провести прямую можем через две точки, если они лежат в одной плоскости. При построении сечений куба возможен еще один вариант построения следа секущей плоскости. Поскольку две параллельные плоскости третья плоскость пересекает по параллельным прямым, то, если в одной из граней уже построена прямая, а в другой есть точка, через которую проходит сечение, то можем провести через эту точку прямую, параллельную данной.
Рассмотрим на конкретных примерах, как построить сечения куба плоскостью.
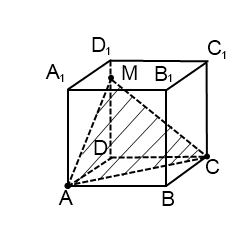
1) Построить сечение куба плоскостью, проходящей через точки A, C и M.
Задачи такого вида — самые простые из всех задач на построение сечений куба. Поскольку точки A и C лежат в одной плоскости (ABC), то через них можем провести прямую. Ее след — отрезок AC. Он невидим, поэтому изображаем AC штрихом. Аналогично соединяем точки M и C, лежащие в одной плоскости (CDD1), и точки A и M, которые лежат в одной плоскости (ADD1). Треугольник ACM — искомое сечение.
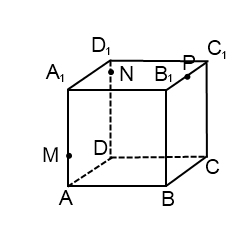
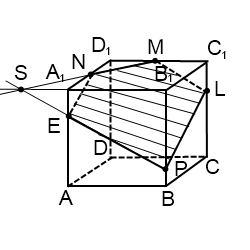
2) Построить сечение куба плоскостью, проходящей через точки M, N, P.
Здесь только точки M и N лежат в одной плоскости (ADD1), поэтому проводим через них прямую и получаем след MN (невидимый). Поскольку противолежащие грани куба лежат в параллельных плоскостях, то секущая плоскость пересекает параллельные плоскости (ADD1) и (BCC1) по параллельным прямым. Одну из параллельных прямых мы уже построили — это MN.
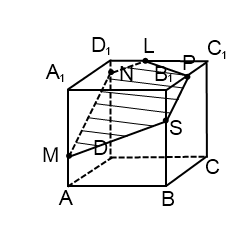
Проводим прямую через точки M и S, лежащие в одной плоскости (ABB1). Получили след MS (видимый).
Плоскости (ABB1) и (CDD1) параллельны. В плоскости (ABB1) уже есть прямая MS, поэтому через точку N в плоскости (CDD1) проводим прямую, параллельную MS. Эта прямая пересекает ребро D1C1 в точке L. Ее след — NL (невидимый). Точки P и L лежат в одной плоскости (A1B1C1), поэтому проводим через них прямую.
Пятиугольник MNLPS — искомое сечение.
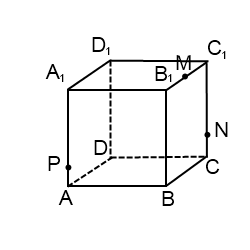
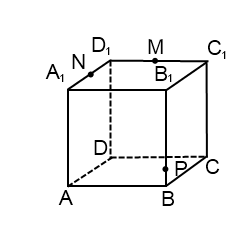
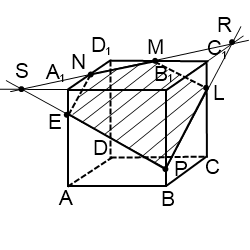
3) Построить сечение куба плоскостью, проходящей через точки M, N, P.
Точки M и N лежат в одной плоскости (ВСС1), поэтому через них можно провести прямую. Получаем след MN (видимый). Плоскость (BCC1) параллельна плоскости (ADD1),поэтому через точку P, лежащую в (ADD1), проводим прямую, параллельную MN. Она пересекает ребро AD в точке E. Получили след PE (невидимый).
Больше нет точек, лежащей в одной плоскости, или прямой и точки в параллельных плоскостях. Поэтому надо продолжить одну из уже имеющихся прямых, чтобы получить дополнительную точку.
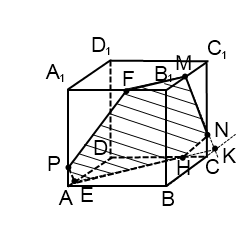
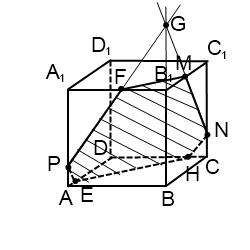
Если продолжать прямую MN, то, поскольку она лежит в плоскости (BCC1), нужно искать точку пересечения MN с одной из прямых этой плоскости. С CC1 и B1C1 точки пересечения уже есть — это M и N. Остаются прямые BC и BB1. Продолжим BC и MN до пересечения в точке K. Точка K лежит на прямой BC, значит, она принадлежит плоскости (ABC), поэтому через нее и точку E, лежащую в этой плоскости, можем провести прямую. Она пересекает ребро CD в точке H. EH -ее след (невидимый). Поскольку H и N лежат в одной плоскости (CDD1), через них можно провести прямую. Получаем след HN (невидимый).
Плоскости (ABC) и (A1B1C1) параллельны. В одной из них есть прямая EH, в другой — точка M. Можем провести через M прямую, параллельную EH. Получаем след MF (видимый). Проводим прямую через точки M и F.
Шестиугольник MNHEPF — искомое сечение.
Если бы мы продолжили прямую MN до пересечения с другой прямой плоскости (BCC1), с BB1, то получили бы точку G, принадлежащую плоскости (ABB1). А значит, через G и P можно провести прямую, след которой PF. Далее — проводим прямые через точки, лежащие в параллельных плоскостях, и приходим к тому же результату.
Работа с прямой PE дает то же сечение MNHEPF.
4) Построить сечение куба плоскостью, проходящей через точку M, N, P.
🔍 Видео
Плоскость. Пересекающиеся прямые. 6 класс.Скачать

Параллельность прямой к плоскостиСкачать

Перпендикулярность прямой и плоскости. 10 класс.Скачать

10 класс, 6 урок, Параллельность прямой и плоскостиСкачать

Взаимное расположение прямых в пространстве. 10 класс.Скачать

№14 из профильного ЕГЭ по математике. Как строить сечения на изи. Серия-1Скачать

Параллельность прямых, плоскостей, прямой и плоскости | Математика ЕГЭ для 10 класса | УмскулСкачать

Параллельность прямых. 10 класс.Скачать

ПАРАЛЛЕЛЬНОСТЬ ПРЯМОЙ и ПЛОСКОСТИ стереометрия 10 классСкачать

Параллельность прямых. Практическая часть. 10 класс.Скачать

№45. Прямая а параллельна стороне ВС параллелограмма ABCD и не лежит в плоскости параллелограмма.Скачать

Принадлежность прямой плоскостиСкачать