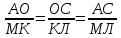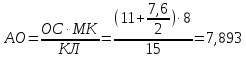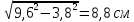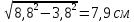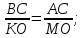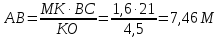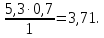Историческая справка проекта подобие треугольников (2 видео)

Историческая справка о подобии

Материал к уроку геометрии 8 класс «подобие треугольников»

Содержание

Скачать:
Подписи к слайдам:
Проектно-исследовательская работа Подобие треугольников в реальной жизни
Просмотр содержимого документа «11Сушко-t.doc»
Просмотр содержимого документа «Подобие треугольников в реальной жизни»
Историческая справка
Подобие треугольников
🔥 Видео

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Скачать:

Вложение	Размер
istoricheskaya_spravka.ppt	2.41 МБ

Предварительный просмотр:

Видео:Подобие треугольников. Вся тема за 9 минут | ОГЭ по математике | Молодой РепетиторСкачать

Подписи к слайдам:

Подготовил: ученик 8 класса Данилов Александр

Треугольник-это простейшая фигура: три стороны и три вершины. Математики его называют двумерным симплексом. «Симплекс» по-латыни означает простейший. Трёхмерным симплексом называют треугольную пирамиду. Именно в силу своей простоты треугольник явился основной многих измерений.

Через площадь треугольника выражается площадь любого многоугольника: достаточно разбить этот многоугольник на треугольники, вычислить их площади и сложить результаты. Правда, верную формулу для площади треугольника удалось найти не сразу. В одном египетском папирусе 4000-летней давности говорится, что площадь равнобедренного треугольника равна произведению половины основания на боковую сторону (а не на высоту).

Через 2000 лет в Древней Греции изучение свойств треугольника ведётся очень активно. Пифагор открывает свою теорему Герон Александрийский находит формулу, выражающую площадь треугольника через его стороны; становится известным, что биссектрисы, как медианы и высоты, пересекаются в одной точке.

Особенно активно свойства треугольника исследовались в XV – XVI веках. Вот одна из красивейших теорем того времени, принадлежащая Леонарду Эйлеру: «Середины сторон треугольника, основания его высот и середины отрезков высот от вершины до точки их пересечения лежат на одной окружности». Эта окружность получила название «окружности девяти точек».

Император Франции Наполеон свободное время посвящал занятиям математикой. Ему приписывают такую красивую теорему: « Если на сторонах треугольника во внешнюю сторону построить равносторонние треугольники, то их центры будут вершинами равностороннего треугольника». Этот треугольник называется внешним треугольником Наполеона.

ТЕОРИЯ Для определения вида треугольника можно сравнить квадрат наибольшей стороны с суммой квадратов двух других сторон. Пусть, например, с – наибольшая сторона. Тогда: А) Если с² а²+в², то треугольник тупоугольный .

Треугольник ABC подобен треугольнику A1B 1 C 1 (обозначение: ABC

т.Фалеса : Если параллельные прямые отсекают от угла с вершиной A треугольники AB 1 C 1 и AB 2 C 2, то эти треугольники подобны и AB 1 : AB 2 = AC 1 : AC 2 (точки B 1 и B 2 лежат на одной стороне угла, C 1 и C 2 — на другой). А В 1 В 2 С 2 С 1

Видео:Задача на подобие треугольников. А ты сможешь решить? | TutorOnline | МатематикаСкачать

Проектно-исследовательская работа Подобие треугольников в реальной жизни

Работа построениа на исследовании возможности применения подобия треугольников в реоальной жизни, выполнены эксперименты по измерению длины с помощью высотомера.

Просмотр содержимого документа
«11Сушко-t.doc»

ПОДОБИЕ ТРЕУГОЛЬНИКОВ В РЕАЛЬНОЙ ЖИЗНИ

Сушко Дарья Олеговна

Ученица 8 класса

Икаева Марина Александровна

Учитель математики, II категория

Геометрия зародилась в глубокой древности. Мир, в котором мы живем сегодня, также наполнен геометрией. Все предметы, окружающие нас, имеют геометрические формы. Это здания, улицы, растения, предметы обихода. В повседневной жизни часто встречаются фигуры одинаковой формы, но разного размера. Такие фигуры в геометрии называют подобными. Моя работа посвящена подобию треугольников, так как, изучая эту тему на уроках математики, меня заинтересовало, как на практике применяются понятие подобия треугольников и признаки подобия. Актуальность моей темы заключается в том, что без каких — либо инструментов, только опираясь на подобие треугольников, можно измерить высоту столба, колокольни, дерева, ширину реки, озера, оврага, длину острова, глубину пруда и т.д.

Целью работы было найти области применения подобия треугольников в реальной жизни.

Задачами работы были

изучить литературу по данной теме;

изучить историю возникновения понятия подобия;

узнать, где применяется подобие треугольников;

измерить высоту столба при помощи подобия треугольников различными способами;

Объекты и предметы исследования: высота: столб; дерево, модель пирамиды.

В ходе работы были применены следующие методы: обзор литературы, практическая работа, сравнение.

Работа носит практико-ориентированный характер, так как практическая значимость работы заключается в возможности использования результатов исследования на уроках геометрии, в повседневной жизни.

В результате выполнения работы были проведены измерения высоты столба, дерева, моделей, изготовленных автором.

Просмотр содержимого документа
«Подобие треугольников в реальной жизни»

Легенда об измерении Фалесом высоты пирамиды

Понятие подобия фигур. Признаки подобия.

4.1 Определение высоты по тени

4.2. Измерение высоты методом Жюля Верна

4.3. Измерение высоты с помощью высотомера

Геометрия зародилась в глубокой древности. Строя жилища и храмы, украшая их орнаментами, размечая землю, измеряя расстояния и площади, человек применял свои знания о форме, размерах и взаимном расположении предметов, полученные из наблюдений и опытов. Мир, в котором мы живем сегодня, также наполнен геометрией. Все предметы, окружающие нас, имеют геометрические формы. Это здания, улицы, растения, предметы обихода. В повседневной жизни часто встречаются фигуры одинаковой формы, но разного размера. Такие фигуры в геометрии называют подобными. Моя работа посвящена подобию треугольников, так как, изучая эту тему на уроках математики, меня заинтересовало, как на практике применяются понятие подобия треугольников и признаки подобия. Актуальность моей темы заключается в том, что без каких — либо инструментов, можно измерить высоту столба, колокольни, дерева, ширину реки, озера, оврага, длину острова, глубину пруда и т.д.

Целью моей работы было найти области применения подобия треугольников в реальной жизни.

Задачами моей работы были

изучить литературу по данной теме;

изучить историю возникновения понятия подобия;

узнать, где применяется подобие треугольников;

измерить высоту столба при помощи подобия треугольников различными способами;

2. Легенда об измерении Фалесом высоты пирамиды.

С пирамидой связано много таинственных историй и легенд. В один из жарких дней Фалес вместе с главным жрецом храма Изиды прогуливался мимо пирамиды Хеопса.

— Знает ли кто – либо, какова её высота?- спросил он.

— Нет, сын мой, — ответил ему жрец,- древние папирусы не сохранили нам этого. — Но ведь определить высоту пирамиды можно совсем точно и прямо сейчас!- воскликнул Фалес.

— Вот смотрите,- продолжал Фалес,- именно в это время, какой бы мы предмет не взяли, тень от него, если поставить его вертикально, точно высоте предмета! Чтобы воспользоваться тенью для решения задачи о высоте пирамиды, надо было знать уже некоторые геометрические свойства треугольника, — именно следующие два (из которых первое Фалес открыл сам):

1. Что углы при основании равнобедренного треугольника равны, и обратно – что стороны, лежащие против равных углов треугольника, равны между собою; 2. Что сумма углов всякого треугольника равна двум прямым углам.

Только вооружённый этим знанием Фалес вправе был заключить, что, когда его собственная тень равна его росту, солнечные лучи встречают ровную почву под углом в половину прямого, и следовательно, вершина пирамиды, середина её основания и конец её тени должны обозначить равнобедренный треугольник . Этим простым способом очень удобно, казалось бы, пользоваться в ясный солнечный день для измерения одиноко стоящих деревьев, тень которых не сливается с тенью соседних. Но в наших широтах не так легко, как в Египте, подстеречь нужный для этого момент: Солнце у нас низко стоит над горизонтом, и тени бывают равны высоте отбрасывающих их предметов лишь в околополуденные часы летних месяцев. Поэтому способ Фалеса в указанном виде применим не всегда.

Учение о подобии фигур на основе теории отношений и пропорции было создано в Древней Греции в V— IV вв. до н. э. Оно изложено в VI книге «Начал» Евклида(III век до нашей эры), начинающиеся следующим определением: «Подобные прямолинейные фигуры суть те, которые имеют соответственно равные углы и пропорциональные стороны»

3. Понятие подобных фигур.

В жизни мы встречаемся не только с равными фигурами, но и с такими, которые имеют одинаковую форму, но разные размеры. Геометрия называет такие фигуры подобными. Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного пропорциональны сходственным сторонам другого треугольника. Признаки подобия треугольников — геометрические признаки, позволяющие установить, что два треугольника являются подобными без использования всех элементов.

Признаки подобия треугольников.

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то такие треугольники подобны.

Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

4. Измерительные работы с помощью подобия.

4.1. Определение высоты по тени.

Я решила провести эксперимент по определению высоты по тени.

Для этого мне понадобились: фонарик, макет пирамиды, фигурка. Сделать миниатюрную пирамиду для проведения экспериментов несложно. Мне понадобились: лист бумаги; карандаш; линейка; ножницы; клей для бумаги. На листе бумаги я построила развертку пирамиды, в основании которой квадрат со стороной 7,6 см, а баковые грани – равные равнобедренные треугольники с боковой стороной 9,6 см. Высота получившейся пирамиды – 7,9 см. Высота фигурки 8,1 см. Попробуем измерить высоту данной пирамиды по её тени, используя также тень фигурки. В солнечный день я измерила тень пирамиды и фигурки. У меня получилось: 15см — тень фигурки, 13 см — тень пирамиды.

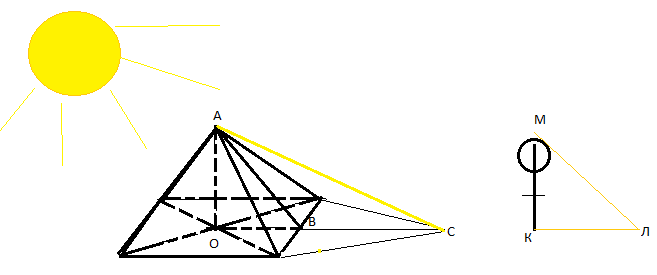
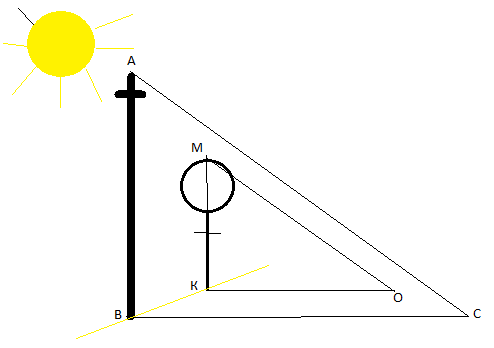
Построим геометрическую модель данной задачи:

Исходные данные задачи: Длина тени пирамиды ВС = 11 см, длина тени фигурки КЛ =15 см, высота фигурки КМ=8 см, основание пирамиды – квадрат со стороной 7,6 см. Высота пирамиды АО – искомое.

Рассмотрим прямоугольные треугольники АОС и МКЛ:

, ∠ АСО= ∠ МЛК как углы падения солнечных лучей, значит по двум углам.

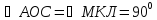
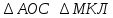
Найдем теперь высоту пирамиды другим способом для сравнения результатов. Найдем высоту боковой грани: АВ=

Из 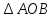найдем высоту АО=

Мы получили практически одинаковые результаты. Получив такие результаты, я решила измерить высоту столба, выйдя на улицу.

Я выбрала столб, от которого падала четкая тень и измерила её. Она равнялась 21 м. Затем я стала рядом со столбом и мой помошник измерил мою тень, она равнялась 4,5 метра. Мой рост, учитывая, что я была в обуви и головном уборе, составил 1,6 .

Найдем высоту столба, составив геометрическую модель задачи.

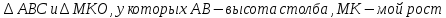
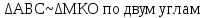
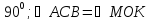
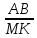
Рассмотрим , КО – длина моей тени, ВС – длина тени столба. АВ – искомое.

∠АВС=∠МКО= как углы падения солнечных лучей.

Таким образом, я получила приблизительное значение высоты столба 7,46 м.

4.2. Измерение высоты пирамиды методом Жюля Верна.

«Таинственный остров» описывает интересный способ определения высоты: «Юноша, стараясь научиться возможно большему, последовал за инженером, который спустился с гранитной стены до окраины берега. Взяв прямой шест, футов 12 длиною, инженер измерил его возможно точнее, сравнивая со своим ростом, который был ему хорошо известен. Герберт же нес за ним отвес, врученный ему инженером: просто камень, привязанный к концу веревки. Не доходя футов 500 до гранитной стены, поднимавшейся отвесно, инженер воткнул шест фута на два в песок и, прочно укрепив его, поставил вертикально с помощью отвеса Затем он отошел от шеста на такое расстояние, чтобы, лежа на песке, можно было на одной прямой линии видеть и конец шеста, и край гребня. эту точку он тщательно пометил колышком.

— Тебе знакомы начатки геометрии? — спросил он Герберта, поднимаясь с земли.

— Помнишь свойства подобных треугольников?

— Их сходственные стороны пропорциональны. — Правильно. Так вот: сейчас я построю два подобных прямоугольных треугольника. У меньшего одним катетом будет отвесный шест, другим — расстояние от колышка до основания шеста; гипотенуза же — мой луч зрения. У другого треугольника катетами будут: отвесная стена, высоту которой мы хотим определить, и расстояние от колышка до основания этой стены; гипотенуза же — мол луч зрения, совпадающий с направлением гипотенузы первого треугольника.

— Понял!—воскликнул юноша.—Расстояние от колышка до шеста так относится к расстоянию от колышка до основания стены, как высота шеста к высоте стены. — Да. И следовательно, если мы измерим два первых расстояния, то, зная высоту шеста, сможем вычислить четвертый, неизвестный член пропорции, т. е. высоту стены. Mы обойдемся, таким образом, без непосредственного измерении этой высоты. Оба горизонтальных расстояния были измерены: меньшее равнялось 15 футам, большее — 500 футам. По окончании измерений инженер составил следующую запись:

15 : 500 = 10:х, 500 X 10 = 5000, 5000 : 15 = 333,3.

4.3 Определение высоты с помощью высотомера

Высоту можно измерить специальным прибором — высотомером. Для изготовления данного прибора потребуется: Плотный белый картон, линейка, ручка, карандаш, ножницы, нитка, грузик, игла.

1. Из картона чертим и вырезаем квадрат размером 15х15см.

2. Делим квадрат на два прямоугольника: 5х15 см, 10х15 см.

3. Прямоугольник 10х15 см делим на две части: 5 см и 10 см.

4. На большей части с длиной 10 см, наносим сантиметровые деления и обозначаем их десятичной дробью, то есть 0,1;0,2 и т.д.

5. В точке Е иглой делаем отверстие и протаскиваем нитку с грузиком, а затем закрепляем нитку сзади.

6. Для того, чтобы было удобнее смотреть, отгибаем верхний прямоугольник от основания.

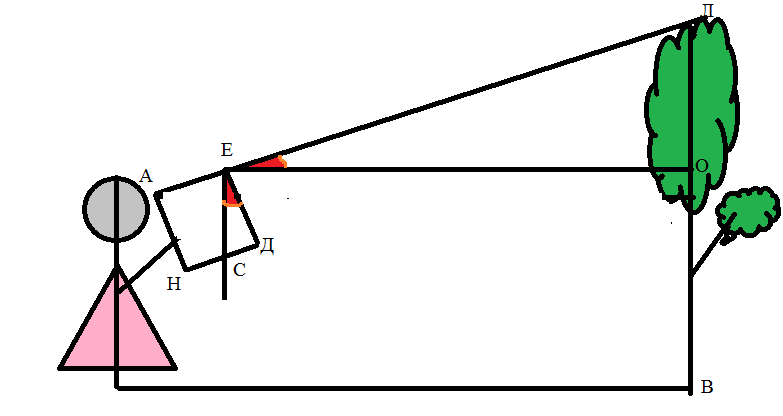
7. На нём с боков отгибаем два прямоугольника размером 3х5 см и прорезаем два отверстия с разным диаметром: одной поменьше — у глаза, другой побольше – для того, чтобы навести на вершину дерева. Итак, я решила провести эксперимент и проверить данный способ измерения высоты предмета. В качестве измеряемого объекта я выбрала дерево, растущее возле школы.

Я отошла от измеряемого предмета на 21 шаг, то есть EO =6,3 м. Я измерила показания прибора, он показывал 0,7. Мой рост 1,6 м. Требуется найти высоту дерева.

Для этого построим геометрическую модель данной задачи:

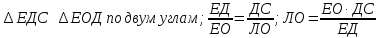
Прибавим к полученной величине мой рост и получим: ЛВ=ЛО+ОВ=3,71

1,6=5,31 – высота дерева.

Также, я могла допустить ошибки в использовании прибора Ошибки в использовании и изготовлении прибора:

1.Если не отгибать верхний прямоугольник от основания, то вы неправильно определите высоту.

2.При измерении высоты предмета, грузик должен быть направлен на конкретную величину разметки.

3.Расстояние от измеряемого объекта должно быть точным.

4.Точно наносить разметку в 1 см.

Эксперимент показал, что метод определения высоты предмета с помощью прибора «высомера» является более точным и удобным.

Выполнив свою работу я узнала о том, что существуют много различных способов определения высоты предмета. Я провела эксперимент по определению высоты предмета по его тени. Испытание я проделала в домашних условиях на модели пирамиды и фигурки, а также на улице при измерении высоты столба. Также, я рассмотрела способ Жюля Верна для определения высоты. Я изучила понятие высотометра и изготовила прибор высотометр, который применила на практике для измерения высоты выбранного объекта. Самым удобным способом измерения высоты для меня пришлось использование высотометра. Таким образом, цели моей работы достигнуты. Можно смело утверждать, что подобие треугольников применяется в реальной жизни при измерительных работах на местности.

1. Глейзер Г.И. История математики в школе. – М.:Издательство «Просвещение», 1964.

2.Перельман Я. И. Занимательная геометрия.– М.:Государственное издательство технико-теоретической литературы, 1950.

3.Ж.Верн. Таинственный остров.- М: Издательство « Детская литература», 1980.

4. Геометрия, 7 – 9: учеб. для общеобразоват. учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – 18-е изд. – М.: Просвещение, 2010 Использованные материалы и интернет-ресурсы .

5. Перельман Я. И. Занимательная геометрия.– М.:Государственное издательство технико-теоретической литературы, 1950
Измерять высоту дерева можно 3-мя способами.

Видео:Геометрия 8 класс (Урок№15 - Признаки подобия треугольников.)Скачать

Историческая справка

Скачать
презентациюУсталый чужеземец >>

Историческая справка. За шесть веков до нашей эры греческий мудрец Фалес Милетский вычислил высоту египетской пирамиды, измерив длину её тени. Как это было, рассказывается в книге Я.И.Перельмана «Занимательная геометрия». Фалес, говорит предание, избрал день и час, когда длина собственной его тени равнялась его росту. В этот момент высота пирамиды должна также равняться длине отбрасываемой его тени. Вот, пожалуй, единственный случай, когда человек извлёк пользу из своей тени. ПРИТЧА:

Слайд 7 из презентации «Применение подобия треугольников в жизни» к урокам геометрии на тему «Подобие треугольников»

Размеры: 960 х 720 пикселей, формат: jpg. Чтобы бесплатно скачать слайд для использования на уроке геометрии, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как. ». Скачать всю презентацию «Применение подобия треугольников в жизни.ppt» можно в zip-архиве размером 5086 КБ.

Видео:8 класс, 22 урок, Первый признак подобия треугольниковСкачать

Подобие треугольников

«Признаки подобия» — Признаки подобия треугольников. Определение подобных треугольников. Дано: ?АВС, ?А1В1С1 AB/A1B1=BC/B1C1=CA/C1A1. Доказательство теоремы. Второй признак подобия треугольников. Доказать: 16. Третий признак подобия треугольников. Подобные треугольники. Итак, стороны треугольника АВС пропорциональны сходственным сторонам треугольника А1В1С1.

«Отношение площадей подобных треугольников» — Содержание. Отношение периметров двух подобных треугольников равно коэффициенту подобия. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. Отношение площадей подобных треугольников. Подобные треугольники. В повседневной жизни встречаются предметы одинаковой формы, но разных размеров.

«Задачи на подобие треугольников» — Прямоугольные треугольники. Треугольник. Произведение отрезков. Окружность. Доказательство. Остроугольный треугольник. Две прямые. Сформулируйте первый признак подобия треугольников. Вершина. Периметр. Найдите произведение отрезков. Хорды окружности. Укажите все подобные треугольники. Изобразите треугольник.

«Задачи на подобие» — Пример № 5. Пример № 3. Пример № 7. Второй и третий признаки подобия треугольников. Первый признак подобия треугольников. Пример № 6. Подобные треугольники. Пример № 2. Пример № 1. Решение задач по геометрии на готовых чертежах. Пример № 4. Темы задач.

«Признаки подобия треугольников» — Признаки подобия треугольников. Существует три признака подобия: А в а1в1. 3. Признак подобия треугольников по трем сторонам. Подобие прямоугольных треугольников. 1. Признак подобия треугольников по двум углам.

«Первый признак подобия треугольников» — Значит, по определению, треугольники подобны. Что значит, что ? АВС подобен треугольнику ? A1В1С1? Стороны треугольника равны 5 см, 8 см и 10 см. Сходство, подобие. Найдите наименьший угол второго треугольника. В трапеции ABCD (BC||AD) проведите диагонали и найдите образовавшиеся подобные треугольники.

Всего в теме «Подобие треугольников» 23 презентации