В треугольник авс вписана окружность радиуса r касающаяся стороны ac

Цена занятия фиксированная и не зависит от их количества в пакете!

Наши репетиторы

Вопрос ученика

Вчера в 8:26 утра

Вписанная окружность треугольника АВС касается сторон АВ, ВС и АС в точках М, N и К соответственно. Прямая MN пересекает прямую АС в точке Р, при этом РС = АС. В каком отношении точка К делит сторону АС?

Ответ репетитора

Предметы: Математика, Геометрия, Алгебра, Подготовка к ЕГЭ, Физика, Подготовка к ОГЭ

Пусть точка К делит сторону AC в отношении k:1, считая от точки А. Тогда АМ = АК = k, CN = CK =1, PC = AC = k+1.

Соединим вершину В треугольника с центром О окружности, продолжим отрезок ВО до пересечения со стороной ОС в точке L. По теореме о биссектрисе внутреннего угла треугольника АВ:ВС = AL:LC, поэтому, если обозначить BM=BM = x, а радиус вписанной окружности за r, то полупериметр треугольника ABC равен p = k+1+x, площадь S треугольника ABC будет равна S = pr = (k+1+x)r. C другой стороны, площадь треугольника ABC можно выразить через произведение длины одной из его сторон на длину перпендикуляра к этой стороне.

Заметим, что данная окружность является вневписанной для треугольника PNC, значит, по теореме о расстоянии до точки касания длина отрезка PQ, где за Q обозначена точка касания, отличная от точки K, получаем соотношение PQ = p2(полупериметр треугольника PRC) =(1+(1+k)+PR)/2

А так как произведение длины отрезка секущей на длину её внешней части равно квадрату длины касательной, проведённой из той же точки, то MN*PN = PK*PK или (2+k)*(2+k)=MN*PN

Ответ:точка К касания вписанной окружности со стороной АС делит ее в отношении 2:1, считая от вершины А.

Видео:№693. В прямоугольный треугольник вписана окружность радиуса r. Найдите периметр треугольника,Скачать

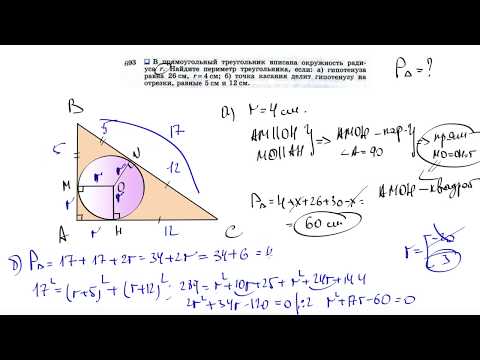
В треугольнике ABC вписана окружность радиуса R, касающаяся стороны AC в точке D, причем AD = R?

Геометрия | 5 — 9 классы

В треугольнике ABC вписана окружность радиуса R, касающаяся стороны AC в точке D, причем AD = R.

1) Докажите, что треугольник ABC равнобедренный Нужно решение с чертежом.

Решение задания во вложении.

Видео:Геометрия В треугольник ABC вписана окружность радиуса R, касающаяся стороны AC в точке D, причёмСкачать

Основание AC равнобедренного треугольника ABC равно 18?

Основание AC равнобедренного треугольника ABC равно 18.

Окружность радиуса 13 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине.

Найдите радиус окружности, вписанной в треугольник ABC.

Видео:Задача о треугольнике из тренировочного варианта ЕГЭСкачать

Основание AC равнобедренного треугольника ABC равно 12?

Основание AC равнобедренного треугольника ABC равно 12.

Окружность радиуса 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания AC.

Найдите радиус окружности, вписанной в треугольник ABC.

Видео:Задача 16. ЕГЭ по математике. Профиль. Урок 1Скачать

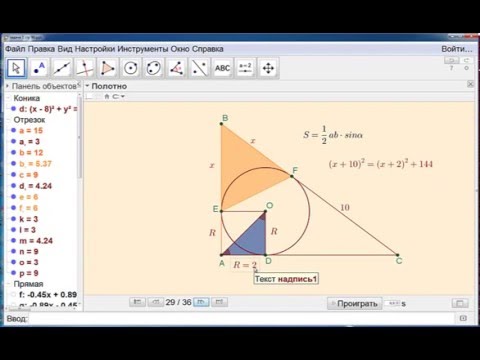
В треугольник MNK вписана окружность радиуса R, касающаяся стороны MK в точке Р, причём MP = R?

В треугольник MNK вписана окружность радиуса R, касающаяся стороны MK в точке Р, причём MP = R.

Докажите, что треугольник MNK равнобедренный.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Расстояние между параллельными прямыми равно 4?

Расстояние между параллельными прямыми равно 4.

На одной из них лежит точка C, а на другой — точки A и B, причем треугольник ABC — остроугольный равнобедренный, и его боковая сторона равна 5.

Найдите радиус окружности, вписанной в треугольник ABC.

Видео:В треугольник АВС вписана окружность, которая касается АВ в точке РСкачать

Основание AC равнобедренного треугольника ABC равно 18?

Основание AC равнобедренного треугольника ABC равно 18.

Окружность радиуса 12 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине.

Найдите радиус окружности, вписанной в треугольник ABC.

Видео:9.52.1. Планиметрия. Гордин Р.К.Скачать

В треугольник ABC вписана окружность, касающаяся его в точках L, M и N?

В треугольник ABC вписана окружность, касающаяся его в точках L, M и N.

Докажите, что треугольник KLM — всегда остроугольный.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Основание AC равнобедренного треугольника ABC равно 12?

Основание AC равнобедренного треугольника ABC равно 12.

Окружность радиуса 8 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине.

Найдите радиус окружности, вписанной в треугольник ABC.

Видео:ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать

Помогите?

Дан треугольнис ABC.

Окружность вписана в треугольник и касается стороны AC в точке М.

Докажите, что BM меньше утроенного радиуса окружности.

Видео:✓ Простое решение красивой геометрии | Планиметрия | Физтех-2021. Математика | Борис ТрушинСкачать

Окружность вписанная в равнобедренный треугольник ABC касается его боковых сторон AB и BC в точках M и N соответственно ?

Окружность вписанная в равнобедренный треугольник ABC касается его боковых сторон AB и BC в точках M и N соответственно .

Докажите что MN перпендикулярна AC.

Видео:11.46.1. Планиметрия. Гордин Р.К.Скачать

Помогите?

Дан треугольнис ABC.

Окружность вписана в треугольник и касается стороны AC в точке М.

Докажите, что BM меньше утроенного радиуса окружности.

Перед вами страница с вопросом В треугольнике ABC вписана окружность радиуса R, касающаяся стороны AC в точке D, причем AD = R?, который относится к категории Геометрия. Уровень сложности соответствует учебной программе для учащихся 5 — 9 классов. Здесь вы найдете не только правильный ответ, но и сможете ознакомиться с вариантами пользователей, а также обсудить тему и выбрать подходящую версию. Если среди найденных ответов не окажется варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском», который откроет все похожие ответы, или создайте собственный вопрос, нажав кнопку в верхней части страницы.

Видео:ЕГЭ Задание 16 Две окружностиСкачать

Задание №16 ЕГЭ (профильный уровень)

В прямоугольный треугольник АВС с прямым углом А

и катетами АВ = 3; АС = 5 вписан квадрат ADEF.
а) Докажите, что треугольники BDE и EFC подобны.
б) Найдите отношение площади треугольника EFC к площади квадрата ADEF.

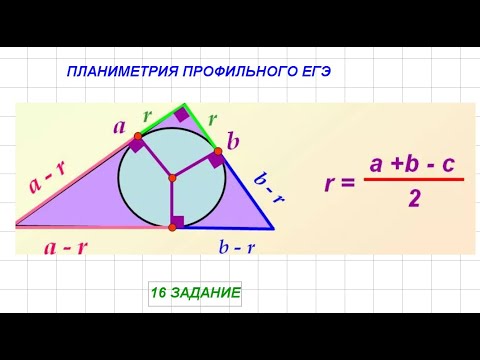
2. Вневписанная в треугольник АВС окружность касается его боковой стороны и продолжения основания АС.

а) Докажите, что радиус этой окружности равен высоте ВН треугольника АВС.

б) Найдите площадь треугольника АВС, если радиус окружности равен 8, а АС·АВ = 120.

3. Две окружности касаются внешним образом в точке L. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.

а) Докажите, что прямые AD и BC параллельны.

б) Найдите площадь треугольника ALB, если известно, что радиусы окружностей равны 8 и 2.

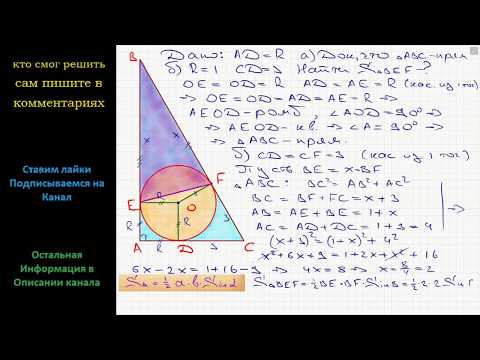
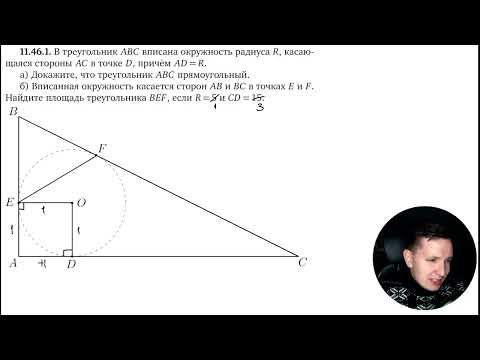
4. В треугольник ABC вписана окружность радиуса R, касающаяся стороны AC в точке D, причём AD= r.

а) Докажите, что треугольник ABC прямоугольный.

б) Вписанная окружность касается сторон AB и BC в точках M и N. Найдите площадь треугольника BMN, если известно, что r= 1 и CD =3.

5. Дан треугольник АВС. Серединный перпендикуляр к стороне АВ пересекается с биссектрисой угла ВАС в точке К, лежащей на стороне ВС.

а) Докажите, что АС2 =ВС·СК.

б) Найдите радиус окружности, вписанной в треугольник АКС, если sinВ = 0,8 и сторона АС= 30.

🔥 Видео

Вписанная и описанная окружность - от bezbotvyСкачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

Радиус описанной окружностиСкачать

Задача 6 №27916 ЕГЭ по математике. Урок 133Скачать

Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Треугольник ABC вписан в окружность с центром O Угол BAC равен 32°Скачать

#99. КАК РЕШАТЬ №16 ЕГЭ ПО МАТЕМАТИКЕ?Скачать