Сколько градусов полная дуга окружности

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

• Определение окружности

• Отрезки в окружности

Определение окружности

Окружность – геометрическое место точек, равноудаленных от данной точки.

Эта точка называется центром окружности .

Отрезки в окружности

Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.

Хорда a – отрезок, соединяющий две точки на окружности.

Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).

O A – радиус, D E – хорда, B C – диаметр.

Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.

Касательная к окружности – прямая, имеющая с окружностью одну общую точку.

Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.

Теорема 2:
Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).

Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.

Дуга в окружности

Часть окружности, заключенная между двумя точками, называется дугой окружности .

Например, хорда A B стягивает две дуги: ∪ A M B и ∪ A L B .

Теорема 4:
Равные хорды стягивают равные дуги.

Если A B = C D , то ∪ A B = ∪ C D

Углы в окружности

В окружности существует два типа углов: центральные и вписанные.

Центральный угол – угол, вершина которого лежит в центре окружности.

∠ A O B – центральный.

Центральный угол равен градусной мере дуги, на которую он опирается . ∪ A B = ∠ A O B = α

Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.

Градусная мара всей окружности равна 360 ° .

Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.

∠ A C B – вписанный.

Вписанный угол равен половине градусной меры дуги, на которую он опирается . ∠ A C B = ∪ A B 2 = α 2 ∪ A B = 2 ⋅ ∠ A C B = α

Теорема 5:
Вписанные углы, опирающиеся на одну и ту же дугу, равны .

∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2

Теорема 6:
Вписанный угол, опирающийся на полуокружность (на диаметр), равен 90 ° .

∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 °

Длина окружности, длина дуги

Мы узнали, как измеряется градусная мера дуги окружности (она равна градусной мере центрального угла, который на нее опирается) и всей окружности целиком (градусная мера окружности равна 360 ° ). Теперь поговорим о том, что же такое длина дуги в окружности. Длина дуги – это значение, которое мы бы получили, если бы мерили дугу швейным сантиметром. Рассмотрим две окружности с разными радиусами, в каждой из которых построен центральный угол равный α .

Градусная мера дуги ∪ A B равна градусной мере дуги ∪ C D и равна α .

Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.

Длина окружности находится по формуле:

Длина дуги окружности , на которую опирается центральный угол α равна:

l α = π R 180 ∘ ⋅ α

Площадь круга и его частей

Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.

Круг – часть пространства, которая находится внутри окружности.

Иными словами, окружность – это граница, а круг – это то, что внутри.

Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.

Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.

Площадь круга находится по формуле: S = π R 2

Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Примеры сектора в реальной жизни: кусок пиццы, веер.

Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α

Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.

Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.

Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.

S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α

Теорема синусов

Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:

a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с окружностями.

Окружность

Окружность — это геометрическая фигура, которая состоит из
всех точек плоскости, расположенных на заданном расстоянии
от данной точки.

Для решения задач, связанных с окружность, нужно знать её свойства.
Свойства окружности, как и любой другой фигуры зависят от
формы, размеров и так далее. В этой статье мы расскажем вам о
свойства окружности и об основных терминах,
таких как: хорда, радиус, дуга и так далее.

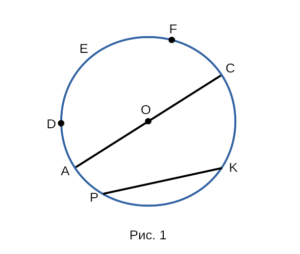
На рисунке 1 изображена окружность, где O — центр окружности,
PK — хорда, AO — радиус, АС — диаметр, DEF — дуга.

Центром окружности называется точка откуда берет начало радиус.
Расположена эта точка в центре окружности. Если внутри окружности
точка расположена на равном расстоянии от всех точек плоскости,
значит это центр окружности. O — центр окружности.

Отрезком соединяющим центр окружности и любую из точек плоскости
называют радиусом. Если отрезок внутри окружности соединяет центр
окружности с любой из точек плоскости, значит этот отрезок — радиус.
CO — радиус.

Отрезок, который соединяет две точки окружности, называется хордой.
Если отрезок внутри окружности соединяет любые две точки окружности,
значит этот отрезок — хорда. PK — хорда.

Отрезок, соединяющий две любые точки окружности и проходящий через
центр окружности, называется диаметром. Если отрезок внутри окружности
соединяет любые две точки окружности и проходит через центр окружности,
значит этот отрезок диаметр. Диаметр в два раза больше радиуса. AC — диаметр.

У диаметра есть середина, которая является центром окружности. Две любые
точки окружности делят окружность на две части. Каждая из частей называется
дугой окружности.

Если две любые точки окружности, делят её на две части,
значит эти части — дуги. DEF — дуга.

Для того, чтобы изобразить окружность на чертеже используют циркуль.
Чтобы провести окружность на местности, можно воспользоваться веревкой.

Кругом называется часть плоскости, которая ограничена окружностью.
Если часть плоскости ограничивает окружность, значит эта часть плоскости — круг.

Сумма углов окружности равна 360°.

Формула угла дуги окружности

Дуга́ — одно из двух подмножеств окружности, на которые её разбивают любые две различные принадлежащие ей точки. Любые две точки A и B окружности разбивают её на две части; каждая из этих частей называется дугой.

Если A и B — концы диаметра (то есть центральный угол AOB — развернутый), точка O — центр окружности, то они определяют две равные дуги, называемые полуокружностями. Если угол AOB не развернутый, то одна из двух дуг AB — это часть окружности, лежащая внутри угла AOB; говорят, что она меньше полуокружности, и что вторая дуга больше полуокружности. Эти углы и дуги называют дополнительными.

Дуги можно измерять в угловых единицах. Равные по центральным углам [1] дуги необязательно равны по длине и прямо пропорциональны радиусу окружности. Они равны только при равенстве радиусов окружностей.

Хочешь подготовиться к ОГЭ или ЕГЭ по математике на отлично?

Хочешь проверить свои силы и узнать результат насколько ты готов к ЕГЭ или ОГЭ?

Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».

Основные термины.

Хорошо ли ты помнишь все названия, связанные с окружностью? На всякий случай напомним – смотри на картинки – освежай знания.

Ну, во-первых – центр окружности – такая точка, расстояния от которой до всех точек окружности одинаковые.

Во-вторых – радиус – отрезок, соединяющий центр и точку на окружности.

Радиусов очень много (столько же, сколько и точек на окружности), но длина у всех радиусов – одинаковая.

Иногда для краткости радиусом называют именно длину отрезка «центр – точка на окружности», а не сам отрезок.

А вот что получится, если соединить две точки на окружности? Тоже отрезок?

Так вот, этот отрезок называется «хорда».

Тут есть ещё одно принятое выражение: «хорда стягивает дугу». Вот, здесь на рисунке, например, хорда стягивает дугу . А если хорда вдруг проходит через центр, то у неё есть специальное название: «диаметр».

Так же, как и в случае с радиусом, диаметром часто называют длину отрезка, соединяющего две точки на окружности и проходящего через центр. Кстати, а как связаны диаметр и радиус? Посмотри внимательно. Конечно же, радиус равен половине диаметра.

Кроме хорд бывают еще и секущие.

Вспомнили самое простое?

А теперь – названия для углов.

Центральный угол – угол между двумя радиусами.

Естественно, не правда ли? Стороны угла выходят из центра – значит, угол – центральный.

А теперь – вписанный угол

Вписанный угол – угол между двумя хордами, которые пересекаются в точке на окружности.

При этом говорят, что вписанный угол опирается на дугу (или на хорду) .

Вот здесь иногда возникают сложности. Обрати внимание – НЕ ЛЮБОЙ угол внутри окружности – вписанный, а только такой, у которого вершина «сидит» на самой окружности.

Смотри на картинку:

Измерения дуг и углов.

Длина окружности. Дуги и углы измеряются в градусах и радианах. Сперва о градусах. Для углов проблем нет – нужно научиться измерить дугу в градусах.

Градусная мера (величина дуги) – это величина (в градусах) соответствующего центрального угла

Что здесь значит слово «соответствующего»? Смотрим внимательно:

Видишь две дуги и два центральных угла? Ну вот, большей дуге соответствует больший угол (и ничего страшного, что он больше ), а меньшей дуге соответствует меньший угол.

Итак, договорились: в дуге содержится столько же градусов, сколько в соответствующем центральном угле.

А теперь о страшном – о радианах!

Что же это за зверь такой «радиан»?

Представь себе: радианы – это способ измерения угла … в радиусах!

Угол величиной радиан – такой центральный угол, длина дуги которого равна радиусу окружности.

Тогда возникает вопрос – а сколько же радиан в развёрнутом угле?

Иными словами: сколько радиусов «помещается» в половине окружности? Или ещё по-другому: во сколько раз длина половины окружности больше радиуса?

Этим вопросом задавались учёные ещё в Древней Греции.

И вот, после долгих поисков они обнаружили, что отношение длины окружности к радиусу никак не хочет выражаться «человеческими» числами вроде и т.п.

И даже не получается выразить это отношение через корни. То есть, оказывается, нельзя сказать, что половина окружности в раза или в раз больше радиуса! Представляешь, как удивительно это было обнаружить людям впервые?! Для отношения длины половины окружности к радиусу на хватило «нормальных» чисел. Пришлось вводить букву .

Итак, – это число, выражающее отношение длины полуокружности к радиусу.

Теперь мы можем ответить на вопрос: сколько радиан в развёрнутом угле? В нём радиан. Именно оттого, что половина окружности в раз больше радиуса.

Древние (и не очень) люди на протяжении веков (!) попытались поточнее подсчитать это загадочное число , получше выразить его (хоть приблизительно) через «обыкновенные» числа. А мы сейчас до невозможности ленивы – нам достаточно двух знаков после занятой, мы привыкли, что

Задумайся, это значит, например, что y окружности с радиусом единица длина приблизительно равна , а точно эту длину просто невозможно записать «человеческим» числом – нужна буква . И тогда эта длина окружности окажется равной . И конечно, длина окружности радиуса равна .

Вернёмся к радианам.

Мы выяснили уже, что в развёрнутом угле содержится радиан.

Исходя из этого, можно пересчитать любые углы «в градусах» на углы «в радианах». Для этого нужно просто решить пропорцию! Давай попробуем. Возьмём угол в .

Значит, рад., то есть рад. Таким же образом получается табличка с наиболее популярными углами.

Итак, осознай и не бойся: если ты видишь букву или выражение и т.п., то речь идёт об угле и, по сути, запись через букву всегда выражает, какую часть от развёрнутого угла составляет тот угол, о котором идёт речь. А для убедительности ещё раз взгляни на табличку

от , то есть от

от , то есть от

от , то есть от

это и есть

в раза больше, чем

А это раза по , то есть

Соотношение между величинами вписанного и центрального углов.

Имеет место удивительный факт:

Величина вписанного угла вдвое меньше, чем величина соответствующего центрального угла.

Посмотри, как это утверждение выглядит на картинке. «Соответствующий» центральный угол такой, у которого концы совпадают с концами вписанного угла, а вершина в центре. И при этом «соответствующий» центральный угол должен «смотреть» на ту же хорду ( ), что и вписанный угол.

Почему же так? Давай разберёмся сначала на простом случае. Пусть одна из хорд проходит через центр. Ведь бывает же так иногда, верно?

Что же тут получается? Рассмотрим . Он равнобедренный – ведь и – радиусы. Значит, (обозначили их ).

Теперь посмотрим на . Это же внешний угол для ! Вспоминаем, что внешний угол равен сумм двух внутренних, не смежных с ним, и записываем:

То есть ! Неожиданный эффект. Но и есть центральный угол для вписанного .

Значит, для этого случая доказали, что центральный угол вдвое больше вписанного. Но уж больно частный случай: правда ведь, далеко не всегда хорда проходит прямиком через центр? Но ничего, сейчас этот частный случай нам здорово поможет. Смотри: второй случай: пусть центр лежит внутри .

Давай сделаем вот что: проведём диаметр . И тогда … видим две картинки, которые уже разбирали в первом случае. Поэтому уже имеем, что

Значит, (на чертеже , а )

Ну вот, и остался последний случай: центр вне угла .

Делаем то же самое: проводим диаметр через точку . Все то же самое, но вместо суммы – разность.

Давай теперь сформируем два главных и очень важных следствия из утверждения о том, что вписанный угол вдвое меньше центрального.

Следствие 1

Все вписанные углы, опирающиеся на одну дугу, равны между собой.

Вписанных углов, опирающихся на одну и ту же дугу (у нас эта дуга ) – бесчисленное множество, они могут выглядеть совсем по-разному, но у них у всех один и тот же центральный угол ( ), а значит, все эти вписанные углы равны между собой.

Следствие 2

Угол, опирающийся на диаметр – прямой.

Смотри: какой угол является центральным для ?

Конечно, . Но он равен ! Ну вот, поэтому (а так же ещё множество вписанных углов, опирающихся на ) и равен .

Угол между двумя хордами и секущими

А что, если интересующий нас угол НЕ вписанный и НЕ центральный, а, например, такой:

Можно ли его как-то выразить всё-таки через какие-то центральные углы? Оказывается, можно. Смотри: нас интересует .

a) ( как внешний угол для ). Но – вписанный, опирается на дугу – . – вписанный, опирается на дугу – .

Для красоты говорят:

Угол между хордами равен полусумме угловых величин дуг, заключённых в этот угол.

– так пишут для краткости, но конечно, при использовании этой формулы нужно иметь в виду центральные углы

b) А теперь – «снаружи»! Как же быть? Да почти так же! Только теперь (снова применяем свойство внешнего угла для ). То есть теперь .

И значит, . Наведём красоту и краткость в записях и формулировках:

Угол между секущими равен полуразности угловых величин дуг, заключённых в этот угол.

Ну вот, теперь ты вооружён всеми основными знаниями об углах, связанных с окружностью. Вперёд, на штурм задач!

ОСТАВШИЕСЯ 2/3 СТАТЬИ ДОСТУПНЫ ТОЛЬКО УЧЕНИКАМ YOUCLEVER!

Стать учеником YouClever,

Подготовиться к ОГЭ или ЕГЭ по математике,

А также получить доступ к учебнику YouClever без ограничений.

Основные определения и свойства. Число π

Формулы для площади круга и его частей

Формулы для длины окружности и ее дуг

Площадь круга

Длина окружности

Длина дуги

Площадь сектора

Площадь сегмента

Основные определения и свойства

Фигура	Рисунок	Определения и свойства
Окружность

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки – центра окружности

Дуга

Часть окружности, расположенная между двумя точками окружности

Круг

Конечная часть плоскости, ограниченная окружностью

Сектор

Часть круга, ограниченная двумя радиусами

Сегмент

Часть круга, ограниченная хордой

Правильный многоугольник

Выпуклый многоугольник, у которого все стороны равны и все углы равны

Около любого правильного многоугольника можно описать окружность

Окружность

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки – центра окружности

Дуга

Часть окружности, расположенная между двумя точками окружности

Круг

Конечная часть плоскости, ограниченная окружностью

Сектор

Часть круга, ограниченная двумя радиусами

Сегмент

Часть круга, ограниченная хордой

Правильный многоугольник

Выпуклый многоугольник, у которого все стороны равны и все углы равны

Около любого правильного многоугольника можно описать окружность

Определение 1 . Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.

Определение 2 . Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.

Замечание 1 . Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.

Определение 3 . Числом π (пи) называют число, равное площади круга радиуса 1.

Замечание 2 . Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:

Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.

Формулы для площади круга и его частей

Числовая характеристика	Рисунок	Формула
Площадь круга

,

где R – радиус круга, D – диаметр круга

Площадь сектора

,

если величина угла α выражена в радианах

,

если величина угла α выражена в градусах

Площадь сегмента

,

если величина угла α выражена в радианах

,

если величина угла α выражена в градусах

Площадь круга

,

где R – радиус круга, D – диаметр круга

Площадь сектора

,

если величина угла α выражена в радианах

,

если величина угла α выражена в градусах

Площадь сегмента

,

если величина угла α выражена в радианах

,

если величина угла α выражена в градусах

Формулы для длины окружности и её дуг

Числовая характеристика	Рисунок	Формула
Длина окружности

где R – радиус круга, D – диаметр круга

Длина дуги

если величина угла α выражена в радианах

,

если величина угла α выражена в градусах

Длина окружности

где R – радиус круга, D – диаметр круга

Длина дуги

если величина угла α выражена в радианах

,

если величина угла α выражена в градусах

Площадь круга

Рассмотрим две окружности с общим центром ( концентрические окружности ) и радиусами радиусами 1 и R , в каждую из которых вписан правильный n – угольник (рис. 1).

Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1 .

Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1 , стремится к π , то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R , стремится к числу πR 2 .

Таким образом, площадь круга радиуса R , обозначаемая S , равна

Длина окружности

то, обозначая длину окружности радиуса R буквой C , мы, в соответствии с определением 2, при увеличении n получаем равенство:

откуда вытекает формула для длины окружности радиуса R :

Следствие . Длина окружности радиуса 1 равна 2π.

Длина дуги

Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.

В случае, когда величина α выражена в градусах, справедлива пропорция

из которой вытекает равенство:

В случае, когда величина α выражена в радианах, справедлива пропорция

из которой вытекает равенство:

Площадь сектора

Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.

В случае, когда величина α выражена в градусах, справедлива пропорция

из которой вытекает равенство:

В случае, когда величина α выражена в радианах, справедлива пропорция

из которой вытекает равенство:

Площадь сегмента

Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла.

Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах, получаем

В случае, когда величина α выражена в в радианах, получаем