Трейдинг криптовалют на полном автомате по криптосигналам. Сигналы из первых рук от мощного торгового робота и команды из реальных профессиональных трейдеров с опытом трейдинга более 7 лет. Удобная система мгновенных уведомлений о новых сигналах в Телеграмм. Сопровождение сделок и индивидуальная помощь каждому. Сигналы просты для понимания как для начинающих, так и для опытных трейдеров. Акция. Посетителям нашего сайта первый месяц абсолютно бесплатно .
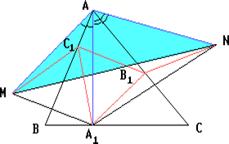
Отсюда следует, что искомый треугольник — это треугольник с вершинами в основаниях высот данного, т.е. ортотреугольник данного треугольника. Действительно, пусть AA», BB» и CC» — высоты треугольника ABC, а точки A1, B1 и C1 расположены на сторонах соответственно BC, AC и AB. Если треугольник A1B1C1 не совпадает с треугольником A»B»C», то по ранее доказанному
P A1B1C1 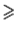

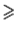

где P и Q — точки пересечения прямой MN со сторонами соответственно AB и AC треугольника ABC. При этом хотя бы один из знаков неравенства — строгий. Значит, искомый треугольник минимального периметра — это треугольник A»PQ. Если бы точка P не совпадала с точкой C», то, повторив предыдущие рассуждения, построили бы треугольник, площадь которого меньше площади треугольника A»PQ, что невозможно. Аналогично для точки Q. Таким образом, точка P совпадает с C», а точка Q — с точкой B».
1. Изложенное решение основано на доказательстве Фейера (L.Fejer). Это, а также другие изящные доказательства данного утверждения (Г.А.Шварц, Л.Шрутка, Бюкнер) см. в книге Г.Радемахера и О.Теплица «Числа и фигуры» (М.,1962, с.36-46).
2. Другой способ доказательства того, что точки P и Q пересечения прямой MN со сторонами соответственно AB и AC также будут основаниями высот треугольника ABC.
Поскольку AM = AA» = AN, то точки M, A» и N лежат на окружности с центром A и радиусом AA». Тогда
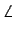
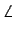
(вписанный угол равен половине соответствующего центрального). Поэтому из точек A и N отрезок A»P виден под одним и тем же углом. Значит, точки A, P, A», N лежат на одной окружности.
С другой стороны, треугольники AA»C и ANC симметричны относительно прямой AC, поэтому они равны. Значит, из точек A» и N отрезок AC виден под прямым углом, поэтому эти точки лежат на окружности с диаметром AC. Поскольку через три точки, не лежащие на одной прямой, проходит ровно одна окружность, то все пять точек A, P, A», C и N лежат на окружности с диаметром AC. Тогда из точки P диаметр AC виден под прямым углом, т.е. CP — высота треугольника ABC. Аналогично докажем, что BQ — также высота треугольника ABC.
В этой курсовой работе я изучила некоторые теоремы, позволяющие решать задачи на экстремумы, проиллюстрировала их применение.
В заключение этой работы, на мой взгляд, следует провести однозначную черту под бесспорным фактом целесообразности и полезности применения ряда задач элементарной геометрии на построение некоторых фигур таким образом, чтобы один из параметров получил наибольшее или наименьшее значение. Во многих случаях решение можно получить без применения методов математического анализа.
1. С.И. Зетель, «Задачи на максимум и минимум», Москва
2. С.А. Теляковский, «Алгебра», Москва, 2001г.
3. Ю.Н. Макарычев, «Математика», Москва, 1988г.
4. Г.С.М. Коксетер, С.П. Грейтцер, «Новые встречи с геометрией», 1978г.
Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Как доказать что треугольник искомый
С помощью линейки с делениями, циркуля, угольника, транспортира, лекал (рис. 313) вам не раз приходилось проводить различные геометрические построения.
А можно ли обходиться меньшим количеством чертёжных инструментов? Оказывается, что во многих случаях достаточно использовать только циркуль и линейку без делений . Например, чтобы провести биссектрису угла, совсем не обязательно иметь транспортир, а разделить отрезок пополам можно и тогда, когда на линейку не нанесена шкала.
А стоит ли в наше время, когда созданы точнейшие приборы и совершенные компьютерные программы, позволяющие выполнять сложнейшие измерения и построения, обходиться такими скудными средствами, как циркуль и линейка? На практике конечно нет. Поэтому, например, конструкторы, строители, архитекторы, дизайнеры не ограничивают себя в выборе инструментов.
Однако при построении фигур в геометрии принимают такие правила:
1) все построения выполняются только с помощью циркуля и ли нейки без делений ;
2) с помощью линейки можно через заданную точку провести произвольную прямую, а также через заданные две точки A и B провести прямую AB ;
3) с помощью циркуля можно построить окружность с данным центром и радиусом, равным заданному отрезку .
Итак, договоримся, что если в задаче требуется построить какую-то фигуру, то построение выполняется по описанным выше правилам.
Решить задачу на построение — это значит составить план ( алгоритм ) построения фигуры; реализовать план, выполнив построение; доказать, что полученная фигура является искомой.
Рассмотрим основные задачи на построение.
Задача 1. Постройте угол, равный данному, одна из сторон которого является данным лучом.
Решение. На рисунке 314 изображены угол A и луч OK . Надо построить угол, равный углу A , одной из сторон которого является луч OK .
Проведём окружность произвольного радиуса r с центром в точке A . Точки пересечения этой окружности со сторонами угла A обозначим B и С (рис. 315). Тогда AB = AC = r .
Проведём окружность радиуса r с центром в точке O . Она пересекает луч OK в точке M (рис. 316, a ). Затем проведём окружность с центром в точке M и радиусом BC . Пусть E и F — точки пересечения окружностей с центрами O и M (рис. 316, б ). Проведём лучи ОЕ и OF (рис. 316, в ).
Покажем, что каждый из углов EOM и FOM — искомый. Докажем, например, что ∠ EOM = ∠ BAC .
Рассмотрим треугольники ABC (рис. 315) и OEM (рис. 316, в ). Имеем: AB = OE = r = AC = OM . Кроме того, по построению EM = BC . Следовательно, треугольники ABC и OEM равны по третьему признаку равенства треугольников. Отсюда ∠ EOM = ∠ BAC . Аналогично можно показать, что ∠ BAC = ∠ FOM .
Замечание. Мы построили два угла ЕОМ и FOM , удовлетворяющие условию задачи. Эти углы равны. В таких случаях считают, что задача на построение имеет одно решение.
Задача 2. Постройте серединный перпендикуляр данного отрезка.
Решение. Пусть AB — данный отрезок (рис. 317, а ). Проведём две окружности с центрами A и B и радиусом AB . Точки пересечения этих окружностей обозначим M и N (рис. 317, б ). Проведём прямую MN (рис. 317, в ).
Из построения следует, что MA = MB = AB и NA = NB = AB (рис. 317, г ). Следовательно, точки M и N принадлежат серединному перпендикуляру отрезка AB . Прямая MN и является серединным перпендикуляром отрезка AB .
Видео:Признаки равенства треугольников. 7 класс.Скачать

Второй и третий признаки равенства треугольников
Содержание
Как мы выяснили несколькими уроками ранее, определять равенство между треугольниками можно задействуя меньше данных о фигурах. Нам удалось познакомиться с одним подобным признаком — по равенству двух сторон и углу между ними. Теперь мы готовы разобрать еще два признака равенства, которые пригодятся вам в течение всего курса геометрии.
Видео:7 класс, 15 урок, Первый признак равенства треугольниковСкачать

Второй признак равенства треугольников
Второй признак равенства треугольников. Если сторона и прилежащие к ней углы одного треугольника соответственно равны стороне и прилежащей к ней углам другого треугольника, то такие треугольники равны.
Пусть имеются треугольники $bigtriangleup$ и $bigtriangleup<A_B_C_>$, у которых равны стороны $AB$ и $A_B_1$ и углы при этих сторонах — $angle=angle,
angle=angle$. Докажем, что треугольники $bigtriangleup$ и $bigtriangleup<A_B_C_>$ равны.
Доказательство. Наложим треугольники друг на друга таким образом, что вершина $A$ совпадет с вершиной $A_1$, а вершины $C$ и $C_1$ будут находиться в одной полуплоскости от стороны $AB$. Поскольку $AB=A_B_1$, вершины $B$ и $B_1$ также совпадут при наложении.
Под вопросом остается расположение вершин $C$ и $C_1$ относительно друг друга. Поскольку $angle=angle,$ по аксиоме откладывания угла равного данному лучи $AC$ и $A_C_1$ будут совпадать. Аналогично совпадение лучей $BC$ и $B_C_$ по равенству углов $angle=angle$.
Раз лучи совпадают, точка пересечения лучей — вершина $C$, то вершина $C_1$ находится в той же точке, что и вершина $C$. Все три вершины совпадают, а значит треугольники $bigtriangleup$ и $bigtriangleup<A_B_C_>$ равны. Теорема доказана .
Запоминать полные формулировки теорем признаков равенства треугольников сложно и может вызвать путаницу. Это придет с опытом решения задач. Пока для вас, возможно, будет удобнее использовать фразу «признак равенства треугольников по…».
Например, второй признак равенства кратко можно перефразировать как «признак равенства треугольников по стороне и прилежащим к ней углам». А как бы вы перефразировали первый?
👍 Все просто: «Признак равенства треугольников по двум сторонам и углу между ними».
Видео:Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

Равнобедренный треугольник: обратная теорема
В точных науках существует понятие обратной теоремы: когда условие исходной теоремы используется в качестве заключения, а заключение — в качестве условия. Чтобы понять, как «работают» обратные теоремы, обратимся для примера к недавно нами доказанной теореме о равнобедренном треугольнике: «В равнобедренном треугольнике углы при основании равны».
— утверждение $A$ — это «равнобедренность треугольника»;
— утверждение $B$ — это «равенство углов при основании».
Логическая операция, к которой мы будем обращаться далее ($Rightarrow$), формально называется импликацией (от лат. ‘implicāre’, в переводе — «впутывать»).
Тогда с точки зрения логики мы можем сказать, что из утверждения $A$ следует утверждение $B$: если $A$, то $B$. Или на языке логики — $ARightarrow$. В обратной теореме утверждения меняются местами — $BRightarrow$, из $B$ следует $A$. В нашем случае читается обратная теорема так: «Если углы при основании равны, то треугольник равнобедренный».
Давайте проверим ее истинность.
Обратная теорема о равнобедренном треугольнике. Если два угла треугольника при основании равны, то такой треугольник является равнобедренным.
Доказательство
Из данного равенства следует, что $AC=BC$. Стороны при основании равны. Тогда $bigtriangleup$ равнобедренный. Теорема доказана.
Об импликациях
Несмотря на то, что прямое и обратное следствия для равнобедренных треугольников оказались истинными, мы не можем, к примеру, сказать то же про вертикальные углы. Действительно, если углы равны… то они вертикальны? Далеко не факт. Иными словами, истинность импликации не гарантирует истинность обратной импликации.
В быту же законы логики соблюдаются редко: мы все время перемешиваем меж собой заключения и условия и, что страшнее, превращаем корреляции в импликации. Например, всем давно известная корреляция между геймингом и детской жестокостью. Нужно понимать, что корреляция — это не более чем статистическая взаимосвязь случайных величин.
Скажем, автомобилист Гриша на третьем перекрестке по дороге домой всегда попадает на зеленый свет светофора. Имеем ли мы право перейти от случайной корреляции к фактическому следствию «если $A$, то $B$»? То есть сказать: «Если Гриша едет домой, то светофор всегда будет зеленым»?
К сожалению, люди размышляют именно так. Корреляция «часто жестокие дети играют в компьютерные игры» превращается в импликацию «если дети играют в игры, то они становятся жестокими».
Или еще хуже, в обратную импликацию: «если ребенок жестокий, то он играет в компьютерные игры».
Первое дает возможность родителям безапелляционно контролировать детей. Второе — снимать какую-либо ответственность за жестокое поведение ребенка с окружения. Импликация — мощное оружие. Особенно когда она используется вне законов науки логики. Так что в следующий раз, если услышите нечто подобное, можете смело заявить о некорректном переходе от корреляции к импликации.
Видео:7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Третий признак равенства треугольников
Третий признак равенства треугольников. Если три стороны одного треугольника соответственно равны трем сторонам второго треугольника, то такие треугольники равны.
Доказательство. Даны два треугольника $bigtriangleup$ и $bigtriangleup<A_B_C_1>$, в которых $AB=A_B_1,
BC=B_C_1$ и $CA=C_A_1$. Наложим треугольники друг на друга так, чтобы вершина $C_1$ располагалась в одной полуплоскости с вершиной $C$. Поскольку $AB=A_B_1,$ точка $A$ совпадет с точкой $A_1,$ точка $B$ совпадет с точкой $B_1$.
Воспользуемся методом доказательства от противного и предположим, что при наложении точка $C_1$ не лежит ни на луче $BC$, ни на луче $AC$. Тогда между вершинами $C$ и $C_1$ имеется расстояние $CC_1$. Обозначим точку $D$ как середину этого отрезка.
Рассмотрим треугольники $bigtriangleup<AC_C>$ и $bigtriangleup<BC_C>$.
Они являются равнобедренными, с общим основанием $CC_1$. В них $AD$ и $BD$ — медианы, поскольку $D$ мы обозначали как середину $CC_1$.
По теореме о медиане равнобедренного треугольника, медианы $AD$ и $BD$ также будут являться высотами соответствующих треугольников. Согласно теореме о единственности перпендикуляра, к точке прямой можно провести только один перпендикуляр. У нас — два перпендикуляра $AD$ и $BD$, к одной точке $D$.
Мы пришли к противоречию. Значит, точка $C_1$ располагается либо на луче $AC$, либо на луче $BC$. Если $C_1in,$ тогда $C_1$ совпадает с точкой $C$, поскольку $CA=C_A_1$. Точно так же приходим к выводу о совпадении точек $C$ и $C_1,$ если $C_1in$. Все три точки совпадают. Треугольники равны.
Теорема доказана .
Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Задача
Попробуйте решить задачу самостоятельно. Ничего страшного, если где-то возникнет заминка: готовое решение находится ниже.
Треугольники $ABC$ и $ABC_1$ равнобедренные, с общим основанием $AB$. Докажите, что треугольники $ACC_1$ и $BCC_1$ равны.
💥 Видео
Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Геометрия 7 класс (Урок№15 - Решение задач на признаки равенства треугольников.)Скачать

Свойства равнобедренного треугольника. 7 класс.Скачать

Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

Теорема о точке пересечения медиан треугольника. Доказательство. 8 класс.Скачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Геометрия. 7 класс. Теоремы. Т6. Второе свойство равнобедренного треугольника.Скачать

Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

7 класс, 16 урок, Перпендикуляр к прямойСкачать

9 класс, 12 урок, Теорема о площади треугольникаСкачать

Высота, биссектриса, медиана. 7 класс.Скачать

Средняя линия. Теорема о средней линии треугольникаСкачать