Официальное объяснение тригонометрии вы можете почитать в учебниках или на других интернет сайтах, а в этой статье мы хотим объяснить суть тригонометрии «на пальцах».
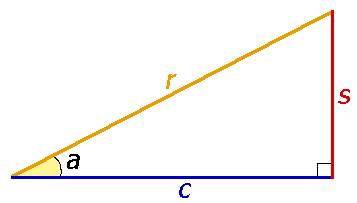
Тригонометрические функции связаны с соотношениями сторон в прямоугольном треугольнике:
- Синус угла – отношение противолежащего катета к гипотенузе;
- Косинус угла – отношение прилежащего катета к гипотенузе;
- Тангенс угла – отношение противолежащего катета к прилежащему;
- Котангенс угла – отношение прилежащего катета к противолежащему.
Или в виде формул:
Для удобства работы с тригонометрическими функциями был придуман тригонометрический круг, который представляет собой окружность с единичным радиусом (r = 1).
Тогда проекции радиуса на оси X и Y (OB и OA’) равны катетам построенного треугольника ОАВ, которые в свою очередь равны значениям синуса и косинуса данного угла.
Тангенс и котангенс получаются соответстсвенно из треугольников OCD и OC’D’, построенных подобно исходному треугольнику OAB.
Для упрощения обучения тригонометрическим функциям в школе используют только некоторые удобные углы в 0°, 30°, 45°, 60° и 90°.
Значения тригонометрических функций повторяются каждые 90° и в некоторых случаях меняя знак на отрицательный.
Достаточно запомнить значения некоторых важных углов и понять принцип повтора значений для бОльших углов.
- Значения тригонометрических функций для первой четверти круга (0° – 90°)
- Принцип повтора знаков тригонометрических функций
- Тригонометрический круг
- Углы в радианах
- Тригонометрический круг: вся тригонометрия на одном рисунке
- А теперь подробно о тригонометрическом круге:
- Геометрия. Урок 1. Тригонометрия
- Тригонометрия в прямоугольном треугольнике
- Тригонометрия: Тригонометрический круг
- Основное тригонометрическое тождество
- Тригонометрия: Таблица значений тригонометрических функций
- Тригонометрия: градусы и радианы
- Тригонометрия: Формулы приведения
- Тригонометрия: Теорема синусов
- Тригонометрия: Расширенная теорема синусов
- Тригонометрия: Теорема косинусов
- Примеры решений заданий из ОГЭ
- Тригонометрия: Тригонометрические уравнения
- 💡 Видео
Значения тригонометрических функций
для первой четверти круга (0° – 90°)
| 0° | 30° | 45° | 60° | 90° | sin | 0 | 1 | √3 | – | ctg | – | √3 | 1 | Принцип повтора знаков тригонометрических функцийУгол может быть как положительный, так и отрицательный. Отрицательный угол считается угол, откладываемый в противоположную сторону. В виду того, что полная окружность составляет 360°, значения тригонометрических функций углов, описывающих одинаковое положение радиуса, РАВНЫ. Например, значения тригонометрических функций для углов 270° и -90° равны. Для лучшего понимания и запоминания значений тригонометрических функций воспользуйтесь динамическим макетом тригонометрического круга ниже. Нажимая кнопки «+» и «–» значения угла будут увеличиваться или уменьшаться соответственно. Видео:Как решать тригонометрические неравенства?Скачать  Тригонометрический кругУглы в радианахДля математических вычислений тригонометрических функций используются углы не в градусах, а в радианах. Что такое радиан? Угол в радианах равен отношению длины дуги окружности к радиусу. Полный круг в 360° соответствует длине окружности 2 π r. Следовательно 360° в радианах равно 2 π , а 180° равно π радиан. Как преобразовывать градусы в радианы? Нужно значение в градусах разделить на 180° и умножить на π . Чтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций. Видео:Решить тригонометрические неравенства sinxСкачать  Тригонометрический круг: вся тригонометрия на одном рисункеТригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое. Вот что мы видим на этом рисунке: Видео:Тригонометрическая окружность. Как выучить?Скачать  А теперь подробно о тригонометрическом круге:Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций. Мы отсчитываем углы от положительного направления оси против часовой стрелки. Полный круг — градусов. Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу . Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу . Всё это легко увидеть на нашем рисунке. Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до : Простым следствием теоремы Пифагора является основное тригонометрическое тождество: Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ). Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы. Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке. Легко заметить, что Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть: где — целое число. То же самое можно записать в радианах: Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению, Видео:10 класс, 22 урок, Простейшие тригонометрические уравнения неравенстваСкачать  Геометрия. Урок 1. ТригонометрияСмотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно. Видео-уроки на канале Ёжику Понятно. Подпишись! Содержание страницы: Видео:ЗНАЧЕНИЯ СИНУСА И КОСИНУСА НА ОКРУЖНОСТИСкачать  Тригонометрия в прямоугольном треугольникеРассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий. Синус угла – отношение противолежащего катета к гипотенузе. sin α = Противолежащий катет гипотенуза Косинус угла – отношение прилежащего катета к гипотенузе. cos α = Прилежащий катет гипотенуза Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу). tg α = Противолежащий катет Прилежащий катет Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу). ctg α = Прилежащий катет Противолежащий катет Рассмотрим прямоугольный треугольник A B C , угол C равен 90 °: sin ∠ A = C B A B cos ∠ A = A C A B tg ∠ A = sin ∠ A cos ∠ A = C B A C ctg ∠ A = cos ∠ A sin ∠ A = A C C B sin ∠ B = A C A B cos ∠ B = B C A B tg ∠ B = sin ∠ B cos ∠ B = A C C B ctg ∠ B = cos ∠ B sin ∠ B = C B A C Видео:9 класс. Геометрия. Тригонометрические функции угла от 0° до 180°. Единичная окружность. Урок #1Скачать  Тригонометрия: Тригонометрический кругТригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга. Тригонометрический круг – это окружность единичного радиуса с центром в начале координат. Такая окружность пересекает ось х в точках ( − 1 ; 0 ) и ( 1 ; 0 ) , ось y в точках ( 0 ; − 1 ) и ( 0 ; 1 ) На данной окружности будет три шкалы отсчета – ось x , ось y и сама окружность, на которой мы будем откладывать углы. Углы на тригонометрической окружности откладываются от точки с координатами ( 1 ; 0 ) , – то есть от положительного направления оси x , против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A . Рассмотрим ∠ S O A , обозначим его за α . Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠ S O A = α = ∪ S A . Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B ) и на ось игрек (точка C ) . Отрезок O B является проекцией отрезка O A на ось x , отрезок O C является проекцией отрезка O A на ось y . Рассмотрим прямоугольный треугольник A O B : cos α = O B O A = O B 1 = O B sin α = A B O A = A B 1 = A B Поскольку O C A B – прямоугольник, A B = C O . Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат). Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° : Опускаем из точки A перпендикуляры к осям x и y . Точка B в этом случае будет иметь отрицательную координату по оси x . Косинус тупого угла отрицательный . Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0 ° до 180 ° . Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x . (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0 ° , 30 ° , 45 ° , 60 ° , 90 ° , 120 ° , 135 ° , 150 ° , 180 ° . Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y . Координата по оси x – косинус угла , координата по оси y – синус угла . Ещё одно замечание. Синус тупого угла – положительная величина, а косинус – отрицательная. Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный . Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный . Видео:Как видеть тангенс? Тангенс угла с помощью единичного круга.Скачать  Основное тригонометрическое тождествоsin 2 α + cos 2 α = 1 Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B : A B 2 + O B 2 = O A 2 sin 2 α + cos 2 α = R 2 sin 2 α + cos 2 α = 1 Видео:10 класс, 11 урок, Числовая окружностьСкачать  Тригонометрия: Таблица значений тригонометрических функций | 0 ° | 30 ° | 45 ° | 60 ° | 90 ° |
|---|---|---|---|---|---|
| sin α | 0 | 1 2 | 2 2 | 3 2 | 1 |
| cos α | 1 | 3 2 | 2 2 | 1 2 | 0 |
| tg α | 0 | 3 3 | 1 | 3 | нет |
| ctg α | нет | 3 | 1 | 3 3 | 0 |
Видео:Синус, косинус произвольного угла. 9 класс.Скачать

Тригонометрия: градусы и радианы
Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!
Видео:Решение неравенства sin t меньше √2/2Скачать

Тригонометрия: Формулы приведения
Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,
можно заметить, что:
sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °
sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °
sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °
sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °
cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °
cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °
cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °
cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °
Рассмотрим тупой угол β :
Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:
sin ( 180 ° − α ) = sin α
cos ( 180 ° − α ) = − cos α
tg ( 180 ° − α ) = − tg α
ctg ( 180 ° − α ) = − ctg α
Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Тригонометрия: Теорема синусов
В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.
a sin ∠ A = b sin ∠ B = c sin ∠ C
Видео:ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ — Синус, Косинус, Тангенс, Котангенс // Подготовка к ЕГЭ по МатематикеСкачать

Тригонометрия: Расширенная теорема синусов
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R
Видео:🔴 ТРИГОНОМЕТРИЯ С НУЛЯ (Тригонометрическая Окружность на ЕГЭ 2024 по математике)Скачать

Тригонометрия: Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A
b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B
c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C
Видео:ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать

Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с тригонометрией.
Видео:Алгебра 10 класс (Урок№31 - Знаки синуса, косинуса и тангенса.)Скачать

Тригонометрия: Тригонометрические уравнения
Это тема 10-11 классов.
Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!
💡 Видео
Решить неравенство tg xСкачать
Решение тригонометрических неравенств. 10 класс.Скачать

Синус, косинус, тангенс и котангенс углов от 0 до 180 градусов.Скачать
Как найти значения синуса и косинуса, НЕ запоминая!Скачать

ТРИГОНОМЕТРИЧЕСКИЕ НЕРАВЕНСТВА 10 класс тригонометрияСкачать







