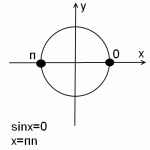Знание — сила. Познавательная информация
Видео:Отбор корней по окружностиСкачать

sinx=0
Эта ассоциация позволяет легко запомнить, где синус равен 0, и быстро решить уравнение sin x=0.
Как обычно, частные случаи синуса рассматриваем на единичной окружности.
Используем ассоциацию косинус-колобок. Оба начинаются с ко-, в названии cos x буква o тоже косвенно на колобка указывает. Колобок движется по горизонтали. На координатной плоскости движение по горизонтали происходит вдоль оси x.
Поэтому cos x — это x, соответственно, sin x — это y.
Таким образом, чтобы найти, где синус равен 0, нужно выяснить, в каких точках y=0.
Раз y=0, то движения вверх-вниз не происходит.
На единичной окружности условию sin x=0 удовлетворяют две точки: 0 и π.
Чтобы из одной точки попасть в другую, надо пройти половину окружности, то есть π.
Поскольку таких точек, в которых синус равен 0, бесконечное множество, прибавляем не π, а πn, где n — целое число (то есть n принадлежит Z): x=0+πn.
Следовательно, решение уравнения sin x=0, есть множество точек
Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Решение тригонометрических уравнений
Данный калькулятор предназначен для решения тригонометрических уравнений.
Тригонометрические уравнения – это уравнения, которые содержат в себе тригонометрические функции неизвестного аргумента. Под тригонометрическими функциями понимают математические функции от величины угла. Как правило, тригонометрические функции определяются как отношения сторон прямоугольного треугольника или длины определенных отрезков в единичной окружности.
К основным видам тригонометрических уравнений относят простейшие уравнения, содержащие модуль, с параметрами, с целой и дробной частью, со сложными аргументами, с обратными тригонометрическими функциями.
С помощью калькулятора можно вычислить корни тригонометрического уравнения.
Для получения полного хода решения нажимаем в ответе Step-by-step.
Видео:РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ😉 #shorts #егэ #огэ #математика #профильныйегэСкачать

Функция y = sin x, её свойства и график
п.1. Развертка ординаты движения точки по числовой окружности в функцию от угла
При движении точки по числовой окружности её ордината является синусом соответствующего угла (см. §2 данного справочника).
Рассмотрим, как изменяется синус, если точка описывает полный круг, и угол x изменяется в пределах: 0≤x≤2π и построим график y=sinx на этом отрезке.
Если мы продолжим движение по окружности для углов x > 2π, кривая продолжится вправо; если будем обходить числовую окружность в отрицательном направлении (по часовой стрелке) для углов x синусоидой .
Часть синусоиды для 0≤x≤2π называют волной синусоиды .
Часть синусоиды для 0≤x≤π называют полуволной или аркой синусоиды .
п.2. Свойства функции y=sinx
1. Область определения (xinmathbb) — множество действительных чисел.
2. Функция ограничена сверху и снизу
Область значений (yin[-1;1])
3. Функция нечётная
4. Функция периодическая с периодом 2π
5. Максимальные значения (y_=1) достигаются в точках
Минимальные значения (y_=-1) достигаются в точках
Нули функции (y_=sinx_0=0) достигаются в точках (x_0=pi k)
6. Функция возрастает на отрезках
$$ -fracpi2+2pi kleq xleqfracpi2+2pi k $$
Функция убывает на отрезках
$$ fracpi2+2pi kleq xleqfrac+2pi k $$
7. Функция непрерывна.
п.3. Примеры
Пример 1. Найдите наименьшее и наибольшее значение функции y=sinx на отрезке:
a) (left[fracpi6; fracright]) $$ y_=sinleft(fracpi6right)=frac12, y_=sinleft(fracpi2right)=1 $$ б) (left[frac; fracright]) $$ y_=sinleft(fracright)=-1, y_=sinleft(fracright)=frac12 $$
Пример 2. Решите уравнение графически:
a) (sinx=3x)
Один корень: x = 0
б) (sinx=2x-2pi)
Один корень: x = π
в) (sinx-sqrt=0)
(sinx=sqrt)
Один корень: x = π
г*) (sinx=left(x-fracpi2right)^2-frac)
(y=left(x-fracpi2right)^2-frac) – парабола ветками вверх, с осью симметрии (x_0=fracpi2) и вершиной (left(fracpi2; -fracright)) (см. §29 справочника для 8 класса)
Два корня: (x_1=0, x_2=pi)
Пример 3. Постройте в одной системе координат графики функций $$ y=sinx, y=-sinx, y=2sinx, y=sinx+2 $$
(y=-sinx) – отражение исходной функции (y=sinx) относительно оси OX. Область значений (yin[-1;1]).
(y=2sinx) – исходная функция растягивается в 2 раза по оси OY. Область значений (yin[-2;2]).
(y=sinx+2) — исходная функция поднимается вверх на 2. Область значений (yin[1;3]).
Пример 4. Постройте в одной системе координат графики функций $$ y=sinx, y=sin2x, y=sinfrac $$
Амплитуда колебаний у всех трёх функций одинакова, область значений (yin[-1;1]).
Множитель под синусом изменяет период колебаний.
(y=sin2x) — период уменьшается в 2 раза, полная волна укладывается в отрезок (0leq xleq pi).
(y=sinfrac) — период увеличивается в 2 раза, полная волна укладывается в отрезок (0leq xleq 4pi).
🎥 Видео
Тригонометрическая окружность. Как выучить?Скачать

Отбор корней по окружностиСкачать

Как решать тригонометрические неравенства?Скачать

Решить тригонометрические неравенства sinxСкачать

🔴 ТРИГОНОМЕТРИЯ С НУЛЯ (Тригонометрическая Окружность на ЕГЭ 2024 по математике)Скачать

Математика| Преобразование тригонометрических выражений. Формулы и задачиСкачать

Простейшие тригонометрические уравнения. y=sinx. 1 часть. 10 класс.Скачать

Уравнение sinx=aСкачать

ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ — Arcsin, Arccos, Arctg, Arcсtg // Обратные тригонометрические функцииСкачать

ТРИГОНОМЕТРИЯ С НУЛЯ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

КОГДА ПИСАТЬ +Пк, а когда +2Пк? (Задание 13 по Тригонометрии ЕГЭ 2024 по Математике Профиль)Скачать

Как решать тригонометрическое уравнение 3cos^2x-sinx-1=0 Замена sinx=t Уравнение с косинусом и синусСкачать

ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ - Решение Тригонометрических уравнений / Подготовка к ЕГЭ по МатематикеСкачать

sinx=0 *BAD MATH*Скачать

4 способа решить уравнение sinx = cosxСкачать
Тригонометрия. Значения синуса и косинуса углов 0°,90°,180°, 270 °, 360° . 10-11 классСкачать

Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать