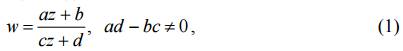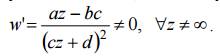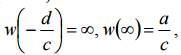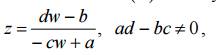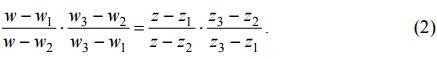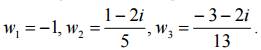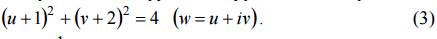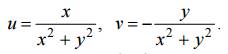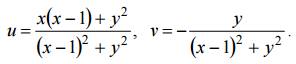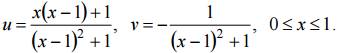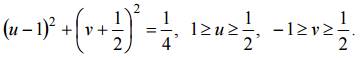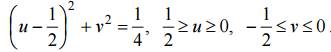Симметрия относительно окружности тфкп

II. Дробно-линейная функция , где ad-dc 0.

Эта функция конформно отображает плоскость на плоскость .

Основные свойства дробно-линейного отображения:

1. Групповые свойства – совокупность дробно-линейных отображений образует группу по отношению к операции суперпозиции.

2. Круговое свойство – дробно-линейное отображение преобразует любую окружность плоскости в окружность плоскости

Замечание . Любая прямая в плоскости считается окружностью бесконечно большого радиуса, проходящей через точку z= .

3 . Свойство сохранения симметрии – при дробно-линейном отображении пара точек, симметричных относительно некоторой окружности, переходит в пару точек, симметричных относительно образа этой окружности.

Замечание. Точки z 1 и z 2 называются симметричными относительно окружности Г, если они лежат на одном луче, выходящем из точки z 0 – центра окружности и | z 1 — z 0 | × | z 2 -z 0 |= r 2 , где r – радиус окружности Г.

4. Существует единственное дробно-линейное отображение, удовлетворяющее условиям: w( z 1 )=w 1 , w( z 2 )=w 2 , w( z 3 )=w 3 , где z 1 , z 2 , z 3 С z , w 1 , w 2 , w 3 C w и это отображение определяется формулой

.

Замечание. Если одна из точек z 1 , z 2 или z 3 , либо w 1 , w 2 или w 3 равна бесконечности, то в последней формуле все разности, содержащие эту точку, следует заменять единицами.

Легко показать, что любую дробно-линейную функцию можно представить в виде , где p , s , q – комплексные числа.

Таким образом дробно-линейная функция есть суперпозиция функций а) t 1 = z + q ; б) ; в) w= p+s t 2 .

Опишем для дробно-линейной функции процесс построения образа Q w области D z , граница g z которой состоит только из дуг окружностей или частей прямых:

а) находим образы угловых точек границы g z , в которых соединяются два соседних участка границы g z ;

б) если дуга окружности (часть прямой) границы g _z расположена на окружности (на прямой), содержащей прообраз бесконечной точки, то соответствующая часть границы Г w образа Q w области D z будет частью прямой. Эта прямая определяется двумя конечными точками плоскости С w ;

в) если дуга окружности (часть прямой) границы g _z расположена на окружности (на прямой), не содержащей прообраз бесконечной точки, то соответствующая часть границы Г w будет частью окружности.

Эта окружность определяется либо по трем конечным точкам плоскости С w , либо по радиусу и центру, который можно найти по свойству сохранения симметрии как точку, симметричную бесконечной точке относительно данной окружности.

г) образ Q w определяется как часть плоскости С w , расположенная слева от кривой Г w , ориентированной в соответствии с ориентацией кривой g _z , либо как часть плоскости С w , ограниченная кривой Г w и содержащая образ какой-нибудь точки области D z .

Видео:ТФКП 14. Свойства ДЛОСкачать

Конформные отображения. Дробно-линейная функция

Видео:Осевая симметрия. 6 класс.Скачать

Конформные отображения. Дробно-линейная функция

Определение 1. Функция вида

где a, b, c, d – комплексные числа, называется дробно-линейной.

Отображение, задаваемое этой функцией, называется дробно- линейным.

Условие ad − bc ≠ 0 означает, что w ≠ const . Функция (1) осуществляет конформное отображение расширенной комплексной плоскости Z на расширенную комплексную плоскость w, так как производная

Для 0 c ≠ предполагаем, что

для c = 0 функция (1) становится линейной, т. е. w = az + b и w(∞) = ∞. Функция

является обратной к функции (1). Она также является дробно-линейной и однозначной на расширенной комплексной плоскости, т. е. здесь функция (1) является однолистной.

Каждое дробно-линейное отображение может быть получено в результате последовательного выполнения трех отображений: линейного, отображения w = 1/z и снова линейного отображения.

Дробно-линейные отображения переводят:

1) окружность или прямую в окружность или прямую (круговое свойство);

2) пару точек, симметричных относительно окружности, – в пару то- чек, симметричных относительно образа этой окружности (свойство сохранения симметрии). Здесь «окружность», в частности, может быть прямой, если под последней понимать окружность бесконечного радиуса.

Существует единственное дробно-линейное отображение, которое три разных точки z₁, z₂, z₃ переводит соответственно в три разные точки w₁, w₂, w₃. Это отображение задается формулой

Если одна из точек z_k или w_k (k =1, 2, 3) является бесконечно удаленной точкой, то в формуле (2) разности, в которые входит z_k или w_k, требуется заменить единицами.

Существует бесконечно много дробно-линейных отображений, которые заданную окружность γ отображают на заданную окружность Г, причем область D, для которой γ является границей, отображается на одну из областей, для которой Г является границей.

Для обеспечения единственности дробно-линейного отображения достаточно выполнение одного из условий:

1) заданная точка z₀ ∈ D отображается в заданную точку w₀ ∈ D’, а любая кривая, выходящая из точки z₀, поворачивается на заданный угол α w₀ = f (z₀), α = arg(f ‘(z₀));

2) точки z₀ ∈ D и z₁ ∈ γ отображаются соответственно в заданные точки w₀ ∈ D’ и w₁ ∈ Γ.

Пример 1. Найти образ окружности, заданной уравнением

x 2 + y 2 + 2x − 4y + 1 = 0,

при отображении w = 1/z.

Решение. На основании кругового свойства дробно-линейного отображения окружность переходит в окружность. Для ее нахождения на заданной окружности x 2 + y 2 + 2x − 4y + 1 = 0, выберем три точки, например: z₁ = −1 z₂ = 1 + 2i, z₃ = −3 + 2i, образами которых при отображении w = 1/z будут точки

Точками w₁, w₂, w₃ однозначно определяется образ данной окружности, уравнение которой:

Для отображения w = 1/z имеем

Выразив отсюда x = x(u, v), y = (u, v) и подставив в уравнение заданной окружности, получим искомый образ (3).

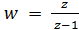
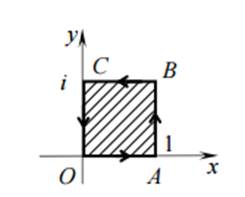
Пример 2. Найти образ области D при отображении , где D = <z, 0

Будем искать образ границы области D (рис. 1).

Сторона OA: y = 0, 0 ≤ x ≤ 1 отображается на отрицательную часть действительной оси (v = 0, − ∞

Рис. 1. Область D

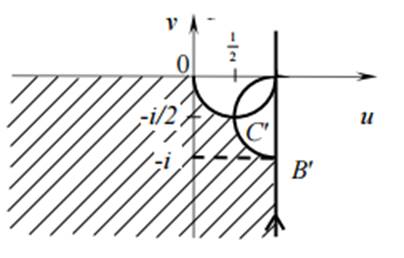
Рис. 2. Образ области D

Сторона AB: x = 1, 0

Сторона BC: y =1, 1 ≥ x ≥ 0, отображается в линию, параметрическое уравнение которой имеет вид

Исключив параметр x, получим

Аналогично образ стороны CO определяется уравнением

В соответствии с принципом соответствия границ образом квадрата будет заштрихованная область на рис. 1.

Пример 3. Найти дробно-линейное отображение, которое точки z₁ = 1 и z₂ = −1 оставляет неподвижными, а точку z₃ = i переводит в точку w₃ = 0.

Найти образ полуплоскости Im(z) > 0 при данном отображении.

Решение. По условию имеем три пары соответствующих точек

Применяя формулу (2), получим искомое дробно-линейное отображение .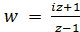

Найдем теперь образ верхней полуплоскости, границей которой является действительная ось. Согласно круговому свойству действительная ось отображается в окружность. Чтобы найти ее, на действительной оси выберем три точки, например: z₁ =1, z₂ = 0, z₃ = −1, образами которых бу- дут точки w₁ = 1, w₂ = −i, w₃ = −1. Они лежат на окружности |w| =1. По принципу соответствия границ получаем, что образом верхней полуплоскости будет область D’= <w, |w|

Пример 4. Найти дробно-линейное отображение, которое круг |z − 4i| u так, что w(4i) = −4, w(2i) = 0.

Решение. Условие задачи определяет две пары соответствующих точек. Третью пару найдем, пользуясь свойством симметрии дробно линейного отображения, согласно которому точки z₁ = 4i и z₃ = ∞, симметричные относительно окружности |z − 4i| = 2, перейдут в точки w₁ = −4 и w₃ = − 4i, симметричные относительно прямой u = v . Таким образом, найдена третья пара точек z₃ = ∞ и w₃ = −4i. По формуле (2) найдем искомое отображение .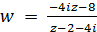

Видео:Ось симметрииСкачать

Сохранение симметрии при дробно-линейном отображении.

Замечание 2. Дробно-линейное отображение преобразует окружность в прямую, если проходит через точку , которая переходит в бесконечно удаленную точку. Если окружность не проходит через точку , то при указанном дробно-линейном отображении перейдет в окружность. Аналогичным образом преобразуются и прямые: прямая при отображении переходит в прямую, если проходит через точку . Иначе переходит в окружность.

Определение 5. Точки и называют симметричными относительно окружности в , если они лежат на одном луче, выходящем из центра окружности , и произведение их расстояний до центра окружности равно квадрату радиуса окружности, т.е. и .

Так как для точек и , симметричных относительно окружности , верно соотношение , то равно действительному положительному числу. А поскольку, согласно определению,

Так как при приближении точки к центру окружности симметричная ей точка стремится к бесконечно удаленной точке, то центр окружности и бесконечности удаленную точку естественно считать симметричными относительно окружности .

Теорема 11. Произвольное дробно-линейное отображение преобразует любые точки и , симметричные относительно окружности на , в точки и , симметричные относительно образа этой окружности.

Рассмотрим семейство всех окружностей на , проходящих через и . Каждая из этих окружностей перпендикулярна . Дробно-линейное отображение переводит каждую окружность в окружность в , перпендикулярную (в силу теоремы : Функция с дополнением и осуществляет взаимно однозначное и непрерывное отображение расширенной комплексной плоскости на расширенную коплексную плоскость ) образу окружности . Согласно критерию симметричности точек, получаем, что точки и , через которые проходят все окружности семейства , симметричны относительно окружности .

🌟 Видео

Лекция №13 по ТФКП. Функция Жуковского. Конформные отображения. Городецкий С.Е.Скачать

Симметрия относительно прямойСкачать

Центральная симметрия. 6 класс.Скачать

Теория функций комплексного переменного 20. Принцип симметрии. Задача Дирихле на плокостиСкачать

СИММЕТРИЯ | осевая симметрия | центральная симметрияСкачать

Белошапка В. К. - Теория функции комплексного переменного I - Лемма Шварца. Принцип симметрииСкачать

Симметрия относительно точки (центральная симметрия). Пример 2Скачать

Савчук А.М. - ТФКП.Часть 1.Семинары - 3. Анализ функций комплексного переменного. ОтображенияСкачать

Нахождение точки, симметричной данной относительно плоскости в пространствеСкачать

лекция 16: принцип симметрииСкачать

Федоровский К.Ю. - ТФКП. Лекции - 13. Конформные отображенияСкачать

Попов В.Ю. - ТФКП. Лекции - 14. Конформные отображенияСкачать

Центральная и осевая симметрии. Геометрия 7 класс.Скачать

Лекция №12 по ТФКП. Дробно-линейные отображения и их свойства. Городецкий С.Е.Скачать

Савчук А.М. - ТФКП.Часть 1.Семинары - 5. Прямая и обратная функция ЖуковскогоСкачать

11 класс, 9 урок, Центральная симметрияСкачать

Консультация по ТФКП. Городецкий С.Е.Скачать