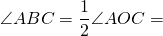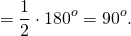Если угол опирается на диаметр окружности то он равен 90 (6 видео)

Вписанный угол, опирающийся на диаметр

Вписанный угол, опирающийся на диаметр, обладает полезным свойством, вытекающим из теоремы о вписанном угле.

Свойство вписанного угла, опирающегося на диаметр

(следствие из теоремы о вписанном угле)

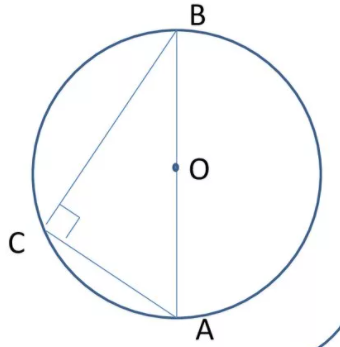
Вписанный угол, опирающийся на диаметр, прямой.

Дано:

Так как AC- диаметр, то ∠AOC=180º.

∠AOC — центральный, ∠ABC — соответствующий ему вписанный угол.

Следовательно, по теореме о вписанном угле,

Что и требовалось доказать.

Из этого следует, например, что если центр описанной окружности лежит на стороне треугольника, то угол напротив этой стороны — прямой.

Если центр описанной окружности лежит на диагонали четырехугольника, то угол напротив этой диагонали — прямой.

Другой вариант формулировки следствия:

Диаметр виден из любой точки окружности под углом 90º.

Если вписанный угол связать с дугой, то следствие из теоремы о вписанном угле звучит так:

Вписанный угол, опирающийся на полуокружность — прямой.

Содержание

Вписанный угол окружности
Теорема о вписанном угле
Следствия из теоремы
Вписанные и центральные углы, их свойства
теория по математике 📈 планиметрия
Вписанный угол
Свойства вписанных углов
Центральный угол
Свойства центральных углов
💡 Видео

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Вписанный угол окружности

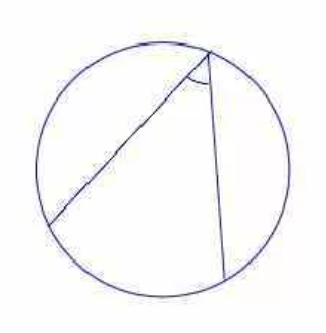
Вписанный угол окружности — это угол, образованный двумя хордами, исходящими из одной точки, то есть вписанным углом называется угол, вершина которого лежит на окружности.

Угол ABC — вписанный угол. ∠ABC опирается на дугу AC, заключённую между его сторонами.

Видео:Вписанный угол, который опирается на диаметрСкачать

Теорема о вписанном угле

Теорема:

Вписанный угол измеряется половиной дуги, на которую он опирается.

Это следует понимать так: вписанный угол содержит в два раза меньше градусов, чем дуга, на которую он опирается:

∠ABC =	1	AC.
	2

При доказательстве этой теоремы следует рассмотреть три возможных случая расположения вписанного угла относительно центра окружности.

Первый случай. Сторона вписанного угла проходит через центр окружности.

Соединим точку A с центром круга (точкой O). Получим равнобедренный треугольник AOB, в котором AO = OB, как радиусы одной окружности. Следовательно, ∠A = ∠B, как углы при основании равнобедренного треугольника.

Так как ∠AOC — внешний угол равнобедренного треугольника, то:

а так как углы A и B равны, то

∠B =	1	∠AOC.
	2

Но ∠AOC — центральный угол, значит ∠AOC = AC, следовательно ∠B измеряется половиной дуги AC:

∠ABC = ∠B =	1	AC.
	2

Второй случай. Центр окружности лежит между сторонами вписанного угла.

Проведём диаметр BD. Угол ABC разбился на два угла: ∠1 и ∠2.

Точка D разделяет дугу AC на две дуги: AD и DC. По доказательству, рассмотренному в первом случае:

∠1 =	1	AD и ∠2 =	1	DC.
	2		2

Следовательно, весь угол ABC будет измеряться половиной дуги AC:

∠1 + ∠2 =	1	AD +	1	DC
	2		2

∠ABC =	1	AC.
	2

Третий случай. Центр окружности лежит вне вписанного угла.

Проведём диаметр BD.

Но ∠ABD измеряется половиной дуги AD , а ∠CBD измеряется половиной дуги CD. Следовательно,

∠ABC =	1	(AD — CD),
	2

∠ABC =	1	AC.
	2

Видео:Вписанные и центральные углы #огэ #огэматематика #математикаСкачать

Следствия из теоремы

1. Все вписанные углы, опирающиеся на одну и ту же дугу, равны между собой, так как они измеряются половиной одной и той же дуги.

2. Вписанный угол, опирающийся на диаметр, — прямой, так как он опирается на половину окружности.

Половина окружности содержит 180°, значит, угол, опирающийся на диаметр, содержит 90°.

Видео:Свойство вписанного угла, опирающегося на диаметрСкачать

Вписанные и центральные углы, их свойства

теория по математике 📈 планиметрия

Видео:Геометрия Докажите что если вершина угла лежит внутри окружности а угол опирается на диаметрСкачать

Вписанный угол

Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают эту окружность.

Свойства вписанных углов

Вписанный угол равен половине дуги, на которую он опирается.

На рисунке показан вписанный угол АСВ и дуга АВ, на которую он опирается. Если, например, дуга АВ=60 0 , то угол АСВ будет равен 30 0 . И наоборот, например, если угол АСВ равен 50 0 , то дуга АВ будет равна 100 0 .

Свойство вписанного угла №2

Вписанные углы, которые опираются на одну и ту же дугу, равны.

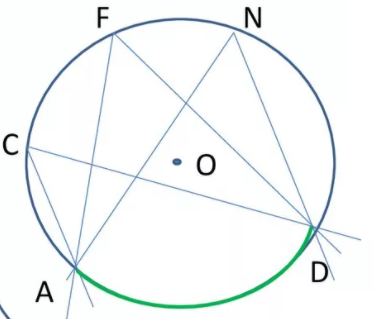
На рисунке показаны три вписанных угла – ACD, AFD, AND, которые опираются на одну и ту же дугу AD, поэтому эти углы равны.

Свойство вписанного угла №2

Вписанный угол, который опирается на диаметр, прямой.

На рисунке угол ВСА опирается на диаметр АВ, следовательно, он равен 90 0 .

Видео:Геометрия Докажите что если вершина угла лежит вне окружности а угол опирается на диаметр окружностиСкачать

Центральный угол

Центральный угол – это угол, вершина которого лежит в центре окружности.

Свойства центральных углов

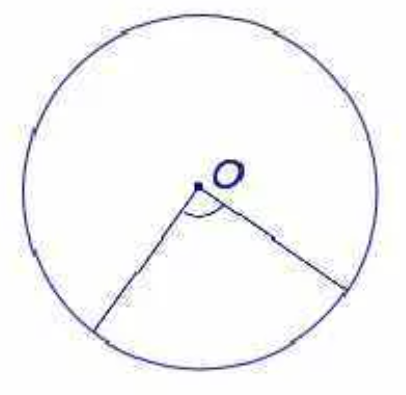
Центральный угол равен дуге, на которую он опирается.

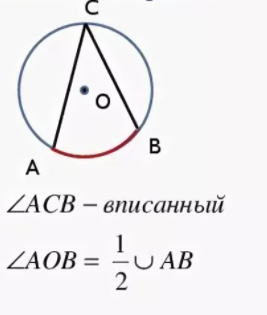
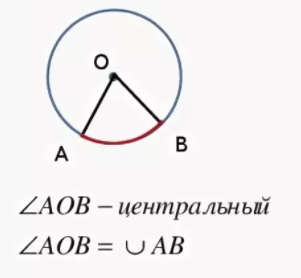
На рисунке показан центральный угол АОВ, который опирается на дугу АВ. Например, дуга АВ равна 80 0 , тогда угол АОВ равен также 80 0 . И наоборот, например, если центральный угол АОВ будет равен 70 0 , то и дуга АВ также будет равна 70 0 .

Свойства вписанного и центрального угла

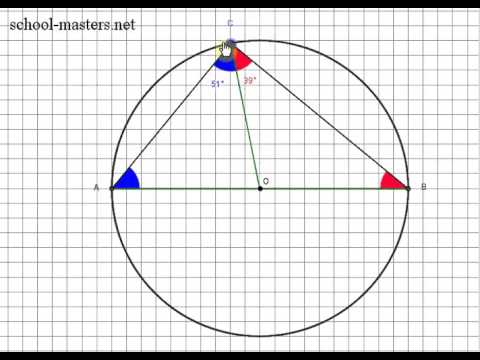
Если центральный и вписанный угол опираются на одну и ту же дугу, то вписанный угол равен половине центрального угла. И наоборот, центральный угол в 2 раза больше вписанного, если они опираются на одну и ту же дугу.

На рисунке показаны вписанный угол АВС и центральный угол АОС, которые опираются на одну и ту же дугу АС. Например, если величина угла АОС равна 120 0 , то величина угла АВС будет равна 60 0 .