Силы равномерно распределенные по дуге окружности (8 видео)

Сосредоточенные силы и распределенные нагрузки

Содержание:

Такие силы называются сосредоточенными. Однако в инженерных расчетах часто приходится встречаться с нагрузками, распределенными вдоль данной поверхности или линии по тому или иному закону. Распределенные силы прежде всего характеризуются интенсивностью q, т.е. величиной силы, приходящейся на единицу поверхности или линии.

На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.

Содержание

Сосредоточенные силы и распределенные нагрузки
Плоская система параллельных сил
Равновесие системы тел
Статически обозначенные и статически неопределенные задачи
Методика решения задач на равновесие системы тел
Силы равномерно распределенные по дуге окружности
Линейно распределенная нагрузка на балку. Построение эпюр в рамах
2 вариант
Распределенные силы
🔥 Видео

Видео:Нагрузка, распределенная по дугеСкачать

Сосредоточенные силы и распределенные нагрузки

Мы рассматривали силы, которые были представлены в виде вектора, приложенного к точке. Однако в природе существует большое количество взаимодействий тел, осуществляются не в точке и которые нельзя представить в виде вектора, приложенного к точке.

Такими силовыми факторами являются силы давления жидкости или газа в поверхность твердых тел, силы тяжести, как массовые силы, электромагнитные силы тому подобное. Поэтому в теоретической механике вводится понятие о распределенных силах, которые делятся на поверхностные и объемные.

Поверхностные силы действуют на некоторую поверхность тела. Объемные силы действуют на каждый элемент объема тела, рассматривается. Примером последних сил является сила притяжения.

В теоретической механике рассматривается воздействие на тело только сосредоточенных сил, приложенных к абсолютно твердым телам. А потому
распределенную нагрузку необходимо заменить его равнодействующей, то есть
сосредоточенной силой. Введем несколько общих положений.

Распределенная нагрузка характеризуется его интенсивностью , то есть величиной силы, приходящейся на единицу объема тела (в случае объемных сил), на единицу площади (в случае поверхностных сил) и на единицу длины (если поверхность, на которую действует нагрузка, можно считать линией, то есть шириной поверхности можно пренебречь). В последнем случае распределенная нагрузка называется плоской, на
силовых схемах оно изображается в виде эпюры элементарных сил, то есть графика интенсивности нагрузки, приложенная к линейному элементу тела.

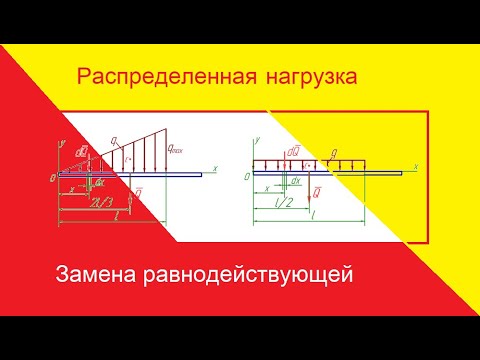
В общем случае распределенная нагрузка изображается в виде определенной кривой, отражающей данный закон изменения интенсивности нагрузки на участке тела (рис. 1.20). Направление действия нагрузки показывается стрелками.

Сначала рассмотрим равномерно распределенную нагрузку и нагрузку, распределенную по линейному закону. Заменяем распределенную нагрузку сосредоточенной силой.

Рассмотрим эти два случая:

— равномерно распределенная нагрузка (или нагрузка, распределенная по закону прямоугольника) изображается на схемах в виде прямоугольника, размеры которого таковы: высота — это интенсивность нагрузки , длина — это длина l участка тела, на которой действует нагрузка. Стрелки показывают направление действия нагрузки (рис. 1.21). Для того, чтобы заменить эту нагрузку равнодействующей силой , надо определить ее. В данном случае

где q — интенсивность нагрузки, Н/м; l — длина участка тела, на которой приложенная нагрузка, м.

Точка C приложения равнодействующей силы размещается посередине участка тела, на которой действует нагрузка. То есть , а направление совпадает с направлением распределенной нагрузки.

— нагрузка распределена по линейному закону (то есть по закону треугольника). В этом случае (рис. 1.22) интенсивность распределенной нагрузки на участке l меняется от 0 до максимального значения q_max. Равнодействующая сила от этой нагрузки по величине равна

Точка C приложения равнодействующей расположена на расстоянии или , а направление совпадает с направлением нагрузки.

Плоская система параллельных сил

Когда линии действия всех сил параллельны, то всегда в плоскости можно так
расположить оси координат, одна из них будет обязательно параллельной заданным силам, а вторая — перпендикулярной. А потому, чтобы тело под действием плоской системы параллельных сил находилось в равновесии, необходимо приравнять к нулю алгебраическую сумму проекций всех сил на параллельную ось и алгебраическую сумму моментов всех сил относительно произвольной точки. В данном случае система условий равновесия (1.54) упрощается и будет иметь такой вид

Для равновесия тела, находящегося под действием системы параллельных сил
на плоскости, необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил
на ось, параллельная силам, и алгебраическая сумма моментов всех сил относительно произвольной точки А плоскости равны нулю.

Для системы параллельных сил на плоскости можно использовать и такие условия равновесия

Для равновесия тела, находящегося под действием системы параллельных сил на плоскости, необходимо и достаточно, чтобы алгебраические суммы моментов всех
сил относительно любых двух точек плоскости равны нулю.

Однако для этих условиях существует ограничение: линия АВ, которой можно соединить
центры моментов, не должна быть параллельной силам.

Данные условия наиболее пригодны при расчетах двухопорных балок. Используя эти условия, составляют алгебраические суммы моментов всех сил относительно точек A и B, в которых установлены опоры балки.

Рассмотрим примеры задач на равновесие тела под действием плоской системы произвольных сил.

Пример:

Однородная балка АВ прямоугольного сечения весом 400 Н имеет один конец А, который закреплен шарнирно, и опирается на точечную опору O (рис. 1.23). Ко второму концу балки В подвешен груз весом 200 Н. Длина балки 4 м, точечная опора расположена на расстоянии ¾ длины балки от шарнирной опоры. Угол наклона балки к горизонту составляет α = 30º.

Определить реакции опор балки.

Краткое условие задачи:

Решение.

Составляем расчетно–силовую схему задачи. Приложим к оси балки заданные активные силы: силу тяжести самой балки и силу притяжения груза. Сила притяжения балки приложена посередине балки в точке C (поскольку балка однородна) и направлена вертикально вниз. Сила притяжения груза приложена к концу балки В и направлена вертикально вниз.

Далее условно освобождаем балку от связей и заменяем их соответствующими реакциями связей. В точке A размещена неподвижная шарнирная опора, она имеет
две составляющие реакции _A и _A, которые расположены вдоль соответствующих осей
координат. В точке O — точечная опора, которая имеет одну реакцию _o, что направлена перпендикулярно к балке.

Таким образом, балка находится в равновесии под действием плоской системы произвольных сил. Для решения этой задачи используем условия равновесия (1.54),

Поскольку оси координат x и y заданные по условию задачи, то составим соответствующие уравнения равновесия

Если подставить значения известных величин в эти уравнения равновесия, то получим

С третьего уравнения вычислим реакцию R_o:

R_o = = 461,86 Н,

и подставим ее значение в первые два уравнения. Будем иметь

Х_А = = R_o = 230,93 Н;

Y_А = 400 + 200 – 0,866 · 461,86 = 160,04 Н.

Поскольку определены две составляющие реакции, приложенные в точке A, — Х_А и Y_А, то геометрическим добавлением можно вычислить модуль полной реакции R_A. А именно:

Таким образом определении все искомые реакции.

Пример.

Определить реакции опоры однородной балки АВ прямоугольного сечения, один конец которого A жестко закреплен в стене и находящийся под действием сосредоточенной силы P = 4,0 kH, пары сил с моментом m = 2,0 kH · м и равномерно распределенной нагрузки интенсивностью q = 1,5 . Длина балки АВ — 5 м, равномерно распределенная
нагрузка действует на участке 3 м от точки A. Угол наклона сосредоточенной силы к горизонту составляет α = 30º, оси x и y показаны на рис. 1.24.

Краткое условие задачи:

q = 1,5 ;

Решение.

Составляем расчетно-силовую схему. Покажем все силы, приложенные к балке АВ. Прежде всего, это заданные активные силы — сила , приложена к концу балки В и направлена под углом α к горизонту. Равномерно распределенную нагрузка заменяем сосредоточенной силой , которая равна

= q · AC =1,5 · 3 = 4,5 kH .

Сила приложена посредине участка AC и направлена в ту же сторону, что и сама нагрузка, то есть вертикально вниз. Покажем на силовой схеме пару сил, которая определяется моментом m.

Далее условно освобождаем балку от вязи и заменяем ее соответствующими реакциями вязи. В точке A — жесткое закрепление балки в стене, а потому оно имеет две составляющие реакции: _A, _A, которые расположены вдоль соответствующих осей
координат, и реактивный момент M_A. Направление этого неизвестного момента
показываем на силовой схеме произвольно, например, — против направления стрелки
часов. Если же при окончательном определении момента M_A получим отрицательный знак, то получим, что действительное направление момента — противоположно. Покажем на силовой схеме линейные и угловые размеры. Оси координат показаны на схеме.

Как видно из построенной расчетно–силовой схемы, балка находится под действием плоской системы произвольных сил. Используем условия равновесия (1.54). А именно = 0.

Составим соответствующие уравнения равновесия

Если подставить значения известных величин в эти уравнения равновесия, то получаем

Из первого уравнения вычислим X_A:

X_A = 4,0 = = 3,46 kH.

Из второго уравнения вычислим Y_A:

Y_A = 4,5 + 4,0 · = 6,50 kH.

С третьего уравнения вычислим M_A:

M_A = 2,0 + 4,5 + 4,0 · 5 = 2,0 + 6,75 + 10,0 = 18,75 kH.

Поскольку составляющие реакций X_A и Y_A, приложенных в точке A, вычислены, то можно найти модуль R_A полной реакции в точке A. Будем иметь

Таким образом, определены все искомые реакции.

Равновесие системы тел

Системой тел называется совокупность нескольких тел, или которые опираются друг на друга, или соединены шарнирами, которые дают возможность относительного движения тел.

При решении задач на систему тел различают силы внешние и внутренние.

Внешние силы — это силы взаимодействия тел данной системы с другими телами, которые не входят в состав системы.

Внутренние силы — это силы взаимодействия между отдельными телами, которые входят в состав данной системы. Внутренние силы существуют попарно, как действие и
противодействие.

Статически обозначенные и статически неопределенные задачи

Задача является статически обозначенной, если для нее можно составить такое
количество уравнений равновесия материальной системы, не меньше, чем число
неизвестных.

Задача, является статически неопределенной, если число уравнений равновесия
системы меньше, чем число неизвестных.

В теоретической механике рассматриваются только статически обозначенные
материальные системы.

Методика решения задач на равновесие системы тел

Равновесие системы тел можно рассматривать в целом под действием только
внешних сил. Но может так случиться, что количество уравнений равновесия будет
меньше, чем количество неизвестных. Тогда необходимо рассматривать равновесие
отдельных тел системы, условно разделяя ее обязательно по внутренним связям. Причем необходимо учитывать, что внутренние силы реакций входят попарно, как действие и противодействие.

Рассмотрим пример решения задач на равновесие системы тел.

Пример.

На трех-шарнирную арку А В С (рис. 1.25) действует вертикальная сила Р = 10 kH. Вес каждой части балки Q₁ = Q₂ = 6 kH. Определить реакции шарниров А, В, С арки, размеры которой данные на рисунке.

Решение.

Как видно из схемы, заданная система тел состоит из двух пиварок I и II, которые соединены шарниром в точке С. Составим расчетно–силовую схему, где покажем заданные активные силы Q₁, Q₂, и реакции связей: в точках A и B (неподвижные шарнирные опоры) — _{A ,}_A и _{В ,} _В и в точке C (шарнирное соединение) — _C , ´_C и _{C ,} ´_С. Эти неизвестные реакции в точке С являются внутренними силами системы тел, а потому _C = ´_C и _C = ´_С.

Покажем оси прямоугольной декартовой системы координат Axy.

Условно разделяем систему тел на два отдельных тела по шарниру С. Действие отброшенной части заменяем двумя реакциями _C и _C, которые равны

Теперь рассмотрим отдельно равновесие каждого тела, для чего составим две системы уравнений равновесия. Используем условия равновесия.

Для первого тела (левая половина арки):

= 0; Х_А — Х_С = 0,

= 0; Y_A + Y_C — Q₁ — P = 0,

= 0; Х_С · 4 + Y_C · 5 — Q₁ · 1 — P · 4 = 0.

Для второго тела (правая половина арки):

= 0; Х_B — Х´_С = 0,

= 0; Y_B + Y´_C — Q₂ — P = 0,

= 0; Q₂ · 1 — Х´_{С ·} 4 + Y´_C · 5 = 0.

Определим эти неизвестные величины. С третьего уравнения второй системы определим Y´_{C .} Перепишем это уравнение следующим образом:

Поскольку численно Y´_C = Y_C , а Х_С = Х´_С, то подставив значения этих реакций в третье уравнение первой системы, получаем

Теперь есть возможность определить неизвестную реакцию Y´_C . Подставив значение X_C в третье уравнение второй системы, будем иметь

Из первого уравнения первой системы имеем X_A = X_C = 6,5 kH. А с первого уравнения второй системы должны X_B = – X´_C = – 6,5 kH. Направление этой реакции противоположно показанному на силовой схеме. Из второго уравнения первой системы получаем

Из второго уравнения второй системы вычислим последнюю неизвестную реакцию Y_B. Она будет равняться Y_B = Y´_C + Q₂ = 4,0 + 6,0 = 10,0 kH.

Таким образом вычислено все искомые величины.

Ответ:

Услуги по теоретической механике:

Учебные лекции:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Распределенная нагрузкаСкачать

Силы равномерно распределенные по дуге окружности

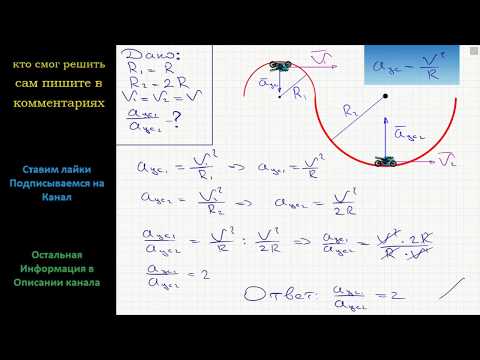
Видео:Физика Тело, равномерно двигавшееся по дуге окружности, перешло на дугу окружности, радиус которойСкачать

Линейно распределенная нагрузка на балку. Построение эпюр в рамах

Post author:writer
Запись опубликована: 05.03.2020
Post category:Заборы и ограждения / Коммуникации / Крыша / Стены и перегородки

Расстояние между сосредоточенными нагрузками одинаковое, при этом расстояние от начала пролета до первой сосредоточенной нагрузки равно расстоянию между сосредоточенными нагрузками. В этом случае сосредоточенные нагрузки также попадают на начало и на конец пролета, но при этом вызывают только увеличение опорной реакции, на значение изгибающих моментов и на прогиб крайние сосредоточенные нагрузки никак не влияют, а потому при расчетах несущей способности конструкции не учитываются. Рассмотрим это на примере балок перекрытия опирающихся на перемычку. Кирпичная кладка, которая может быть между перемычкой и балками перекрытия, и создавать при этом равномерно распределенную нагрузку, для простоты восприятия не показана.

Рисунок 1 . Приведение сосредоточенных нагрузок к эквивалентной равномерно распределенной нагрузке.

Как видно из рисунка 1, определяющим является изгибающий момент, который используется при расчетах конструкций на прочность. Таким образом, чтобы равномерно распределенная нагрузка создавала такой же изгибающий момент, как и сосредоточенная нагрузка, ее нужно умножить на соответствующий коэффициент перехода (коэффициент эквивалентности). А определяется этот коэффициент из условий равенства моментов. Думаю, рисунок 1 это очень хорошо иллюстрирует. А еще, анализируя полученные зависимости, можно вывести общую формулу для определения коэффициента перехода. Так, если количество приложенных сосредоточенных нагрузок является нечетным, т.е. одна из сосредоточенных нагрузок обязательно попадает на середину пролета, то для определения коэффициента эквивалентности можно использовать формулу:

где n — количество пролетов между сосредоточенными нагрузками.

где (n-1) — количество сосредоточенных нагрузок.

Впрочем, иногда удобнее производить расчеты, исходя из количества сосредоточенных нагрузок. Если это количество выразить переменной m, то тогда

При этом эквивалентная равномерно распределенная нагрузка будет равна:

q экв = γmQ/l (305.1.4)

Когда количество сосредоточенных нагрузок является четным, т.е. ни одна из сосредоточенных нагрузок не попадает на середину пролета, то значение коэффициента можно принимать, как для следующего нечетного значения количества сосредоточенных нагрузок. В целом при соблюдении указанных условий загружения можно принимать следующие коэффициенты перехода:

γ = 2 — если на рассматриваемую конструкцию, например, балку попадает только одна сосредоточенная нагрузка посредине перемычки.

γ = 1.33 — для балки, на которую действуют 2 или 3 сосредоточенные нагрузки;

γ = 1.2 — для балки, на которую действуют 4 или 5 сосредоточенных нагрузок;

γ = 1.142 — для балки, на которую действуют 6 или 7 сосредоточенных нагрузок;

γ = 1.11 — для балки, на которую действуют 8 или 9 сосредоточенных нагрузок.

Видео:Преобразование равномерно распределенной нагрузки.Скачать

2 вариант

Расстояние между сосредоточенными нагрузками одинаковое, при этом расстояние от начала пролета до первой сосредоточенной нагрузки равно половине расстояния между сосредоточенными нагрузками. В этом случае сосредоточенные нагрузки не попадают на начало и на конец пролета.

Рисунок 2 . Значения коэффициентов перехода при 2 варианте приложения сосредоточенных нагрузок.

Как видно из рисунка 2, при таком варианте загружения значение коэффициента перехода будет значительно меньше. Так, например, при четном количестве сосредоточенных нагрузок, коэффициент перехода вообще можно принимать равным единице. При нечетном количестве сосредоточенных нагрузок для определения коэффициента эквивалентности можно использовать формулу:

где m — количество сосредоточенных нагрузок.

При этом эквивалентная равномерно распределенная нагрузка все также будет равна:

q экв = γmQ/l (305.1.4)

В целом при соблюдении указанных условий загружения можно принимать следующие коэффициенты перехода:

γ = 2 — если на рассматриваемую конструкцию, например, балку попадает только одна сосредоточенная нагрузка посредине перемычки, а попадают ли балки перекрытия на начало или конец пролета или расположены сколь угодно далеко от начала и конца пролета, в данном случае значения не имеет. А значение это имеет при определении сосредоточенной нагрузки.

γ = 1 — если на рассматриваемую конструкцию, действует четное количество нагрузок.

γ = 1.11 — для балки, на которую действуют 3 сосредоточенные нагрузки;

γ = 1.091 — для балки, на которую действуют 5 сосредоточенных нагрузок;

γ = 1.076 — для балки, на которую действуют 7 сосредоточенных нагрузок;

γ = 1.067 — для балки, на которую действуют 9 сосредоточенных нагрузок.

Не смотря на некоторую заковыристость определения, коэффициенты эквивалентности очень просты и удобны. Так как при расчетах очень часто известна распределенная нагрузка, действующая на квадратный или погонный метр, то чтобы не переводить распределенную нагрузку сначала в сосредоточенную, а потом снова в эквивалентную распределенную, достаточно просто умножить значение распределенной нагрузки на соответствующий коэффициент. Например, на перекрытие будет действовать нормативная распределенная нагрузка 400 кг/м 2 , при этом собственный вес перекрытия составит еще 300 кг/м 2 . Тогда при длине балок перекрытия 6 м на перемычку могла бы действовать равномерно распределенная нагрузка q = 6(400 + 300)/2 = 2100 кг/м. А дальше, если будет только одна балка перекрытия посредине пролета, то γ = 2, а

q экв = γq = 2q (305.2.2)

Если ни одно из двух вышеприведенных условий не соблюдается, то использовать коэффициенты перехода в чистом виде нельзя, нужно добавить еще пару дополнительных коэффициентов, учитывающих расстояние до балок, не попадающих на начало и конец пролета перемычки, а также возможную несимметричность приложения сосредоточенных нагрузок. Вывести такие коэффициенты в принципе можно, однако в любом случае они будут понижающими во всех случаях, если рассматривать 1 вариант загружения и в 50% случаев, если рассматривать 2 вариант загружения, т.е. значения таких коэффициентов будут

В инженерных расчетах часто приходится встречаться с нагрузками, распределенными вдоль данной поверхности по тому или иному закону. Рассмотрим некоторые простейшие примеры распределенных сил, лежащих в одной плоскости.

Плоская система распределенных сил характеризуется ее интенсивностью q, т. е. значением силы, приходящейся на единицу длины нагруженного отрезка. Измеряется интенсивность в ньютонах, деленных на метры

1) Силы, равномерно распределенные вдоль отрезка прямой (рис. 69, а). Для такой системы сил интенсивность q имеет постоянное значение. При статических расчетах эту систему сил можно заменить равнодействующей

Приложена сила Q в середине отрезка АВ.

2) Силы, распределенные вдоль отрезка прямой по линейному закону (рис. 69, б). Примером такой нагрузки могут служить силы давления воды на плотину, имеющие наибольшее значение у дна и падающие до нуля у поверхности воды. Для этих сил интенсивность q является величиной переменной, растущей от нуля до максимального значения Равнодействующая Q таких сил определяется аналогично равнодействующей сил тяжести, действующих на однородную треугольную пластину ABC. Так как вес однородной пластины пропорционален ее площади, то, по модулю,

Приложена сила Q на расстоянии от стороны ВС треугольника ABC (см. § 35, п. 2).

3) Силы, распределенные вдоль отрезка прямой по произвольному закону (рис. 69, в). Равнодействующая Q таких сил, по аналогии с силой тяжести, по модулю равна площади фигуры ABDE, измеренной в соответствующем масштабе, и проходит через центр тяжести этой площади (вопрос об определении центров тяжести площадей будет рассмотрен в § 33).

4) Силы, равномерно распределенные по дуге окружности (рис. 70). Примером таких сил могут служить силы гидростатического давления на боковые стенки цилиндрического сосуда.

Пусть радиус дуги равен , где — ось симметрии, вдоль которой направим ось Действующая на дугу система сходящихся сил имеет равнодействующую Q, направленную в силу симметрии вдоль оси при этом численно

Для определения величины Q выделим на дуге элемент, положение которого определяется углом а длина Действующая на этот элемент сила численно равна а проекция этой силы на ось будет Тогда

Но из рис. 70 видно, что Следовательно, так как то

где — длина хорды, стягивающей дугу АВ; q — интенсивность.

Для определения величины Q выделим на дуге элемент, положение которого определяется углом а длина Действующая на этот элемент сила

Задача 27. На консольную балку А В, размеры которой указаны на чертеже (рис. 71), действует равномерно распределенная нагрузка интенсивностью Пренебрегая весом балки и считая, что силы давления на заделанный конец — определены по линейному закону, определить значения наибольших интенсивностей этих сил, если

Решение. Заменяем распределенные силы их равнодействующими Q, R и R, где согласно формулам (35) и (36)

и составляем условия равновесия (33) для действующих на балку параллельны сил

Подставляя сюда вместо Q, R я R их значения и решая полученные уравнения, найдем окончательно

Например, при получим а при

Задача 28. Цилиндрический баллон, высота которого равна Н, а внутренний диаметр d, наполнен газом под давлением Толщина цилиндрических стенок баллона а. Определить испытываемые этими стенками растягивающие напряжения в направлениях: 1) продольном и 2) поперечном (напряжение равно отношению растягивающей силы к площади поперечного сечения), считая малым.

Решение. 1) Рассечем цилиндр плоскостью, перпендикулярной его оси, на две части и рассмотрим равновесие одной из них (рис.

72, а). На нее в направлении оси цилиндра действуют сила давления на дно и распределенные по площади сечения силы (действие отброшенной половины), равнодействующую которых обозначим Q. При равновесии

Воздействие на детали, конструкции, элементы механизмов может быть задано распределенными нагрузками: в плоской системе задается интенсивность действия по длине конструкции, в пространственной системе – по площади.

Размерность для линейной нагрузки — Н/м, для нагрузки распределенной по площади — Н/м 2 , для объемной (например при учете собственного веса элементов конструкции) — Н/м 3 .

Например, на рисунке 1.23, а приведена равномерно распределенная по длине , измеряемая в Н/м. Эта нагрузка может быть заменена сосредоточенной силой

приложенной в середине отрезка AB .

На рисунке 1.23, б показана равномерно убывающая (возрастающая) нагрузка, которая может быть заменена равнодействующей силой

приложенной в точке C , причем AC = 2/3AB .

В произвольном случае, зная функцию q(x) (рисунок 1.23, в), рассчитываем эквивалентную силу

Эта сила приложена в центре тяжести площади, ограниченной сверху от балки AB линией q(x) .

Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquip ex ea commodo consequat…

Примером может служить расчет усилий, разрывающих стенки баллона со сжатым газом. Определим результирующую силу давления в секторе трубы при интенсивности q [Н/м]; R – радиус трубы, 2α – центральный угол, ось Ox – ось симметрии (рисунок 1.24).

Выделим элемент сектора с углом ∆φ и определим силу ∆Q , действующую на плоский элемент дуги:

∆Q = q ∙ ∆l = q ∙ R ∙ ∆φ . (1.14)

∆Q x = q ∙ R ∙ ∆φ∙ cosφ . (1.15)

В силу симметрии элемента трубы (с дугой AB ) относительно оси Ox проекция результирующей силы на ось Oy :

Q y = 0 , т.е. Q = Q x , (1.16)

где АВ – хорда, стягивающая концы дуги.

Для цилиндрической емкости высотой h и внутренним давлением P на стенки действует нагрузка интенсивностью q = p [Н/м, 2 ] . Если цилиндр рассечен по диаметру (рисунок 1.25), то равна F = q ∙ d ∙ h (d – внутренний диаметр) или

Разрывающие баллон по диаметру усилия:

S 1 = S 2 = S;
2S = F;
S = p∙h∙R . (1.18)

приложенной в середине отрезка AB .

приложенной в точке C , причем AC = 2/3AB .

В произвольном случае, зная функцию q(x) (рисунок 1.23, в), рассчитываем эквивалентную силу

Эта сила приложена в центре тяжести площади, ограниченной сверху от балки AB линией q(x) .

Выделим элемент сектора с углом ∆φ и определим силу ∆Q , действующую на плоский элемент дуги:

∆Q = q ∙ ∆l = q ∙ R ∙ ∆φ . (1.14)

∆Q x = q ∙ R ∙ ∆φ∙ cosφ . (1.15)

В силу симметрии элемента трубы (с дугой AB ) относительно оси Ox проекция результирующей силы на ось Oy :

Q y = 0 , т.е. Q = Q x , (1.16)

где АВ – хорда, стягивающая концы дуги.

Разрывающие баллон по диаметру усилия:

S 1 = S 2 = S;
2S = F;
S = p∙h∙R . (1.18)

Поверхностные и объёмные силы представляют собой нагрузку, распределённую по некоторой поверхности или объёму. Такая нагрузка задаётся интенсивностью , которая представляет собой силу, приходящуюся на единицу некоторого объёма, или некоторой площади, или некоторой длины.

Особое место при решении ряда практически интересных задач занимает случай плоской распределённой нагрузки, приложенной по норма

Плоская фигура, ограниченная балкой и графиком интенсивности нагрузки, называется эпюрой распределённой нагрузки (Рис. 1.28). Если по характеру решаемой задачи можно не учитывать деформации, т.е. можно считать тело абсолютно твёрдым, то распределённую нагрузку можно (и нужно) заменить равнодействующей.

если система сил имеет равнодействующую, то момент равнодействующей относительно любого центра (любой оси) равен сумме моментов всех сил системы относительно этого центра (этой оси)

Очевидно, модуль равнодействующей численно равен площади эпюры распределённой нагрузки, а точка её приложения совпадает с центром тяжести однородной пластины, имеющей форму эпюры распределённой нагрузки.

Отметим два часто встречающихся случая.

В инженерной практике такая нагрузка встречается довольно часто. Равномерно распределённой в большинстве случаев можно считать весовую и ветровую нагрузку.

(Рис. 1.31). В этом случае:

В инженерной практике такая нагрузка встречается довольно часто. Равномерно распределённой в большинстве случаев можно считать в

Найдём равнодействующую распределённой нагрузки. Модуль равнодействующей равен

Определить реакцию заделки консольной балки, находящейся под действием сосредоточенной силы, пары сил и распределённой нагрузки (Рис. 1.34).

Заменим распределённую нагрузку тремя сосредоточенными силами. Для этого разобъём эпюру распределённой нагрузки на два треугольника и прямоугольник. Находим

Силовая схема представлена на Рис. 1.35.

Условия равновесия в рассматриваемом случае имеют вид:

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ:

1. Что называется интенсивностью распределённой нагрузки?

2. Как вычислить модуль равнодействующей распределённой нагрузки?

3. Как вычислить координату точки приложения равнодействующей распределённой

4. Чему равен модуль и какова координата точки приложения равномерно распределённой нагрузки?

5. Чему равен модуль и какова координата точки приложения линейно распределённой нагрузки?

Из сборника задач И.В.Мещерского: 4.28; 4.29; 4.30; 4.33; 4.34.

Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА — теория и практика»: комплекты СР-2; СР-3.

Видео:Определение реакций опор в балке. Сопромат.Скачать

Распределенные силы

Реальные физические взаимодействия тел всегда распределяются по некоторой части их объема или поверхности. Сила, приложенная в геометрической точке. — это лишь удобная абстракция. Покажем способ перехода от распределенной силы к эквивалентной ей сосредоточенной силе — равнодействующей.

Пусть на прямолинейный участок АВ длиной L тонкого стержня действует распределенная сила интенсивностью q(x) Н/м. Это означает, что вблизи точки с координатой .v распределенная сила такова, что на 1 метр длины стержня действует сила с/(х) Н.

Зависимость интенсивности силы от координаты х показана на рис. 4.9 в виде диаграммы АА’В’В — эпюры распределенной силы. Стрелки на эпюре указывают направление распределенной силы.

Разделим отрезок АВ на элементарные участки длиной dx каждый. На элементарный участок [л, x+dx] действует сосредоточенная сила величиной q(x)dx, направленная параллельно распределенной силе (рис. 4.9). Для такой системы параллельных и одинаково направленных сил, так же как и для сил тяжести, можно указать точку С, через которую проходит их равнодействующая. Координату Хс этой точки можно найти, используя равенство величин сил q(x)dx и весов (или площадей) соответствующих элементарных полосок фигуры АА’В’В. В результате точка С определяется как центр тяжести фигуры АА’В’В, а величина равнодействующей — как площадь этой фигуры.

Таким образом, величина равнодействующей силы Q равна площади эпюры распределенной силы, а её линия действия проходит через центр тяжести С этой эпюры.

Рассмотрим наиболее важные для приложений частные случаи.

1. Величина Q равнодействующей равномерно распределенной силы (рис. 4.10) находится как площадь сё прямоугольной эпюры

а линия действия равнодействующей Q проходит через середину нагруженного участка.

2. Величина равнодействующей линейно распределенной силы (рис. 4.11) находится как площадь треугольника

а линия действия равнодействующей проходит через центр тяжести этого треугольника, т.е. на расстоянии Z73 от его основания.

🔥 Видео

Балка с линейно распределенной нагрузкойСкачать

Определение усилий в сечениях арки с треугольной нагрузкойСкачать

Физика | Равномерное движение по окружностиСкачать

Определение реакций опор простой рамыСкачать

Составная рама с распределенной нагрузкойСкачать

Правило знаков для поперечных силСкачать

Классификация сил. Волшебное преобразование нагрузок. Сопромат-Тайные Знания 3.Скачать

Правило рук 👋 КАК ЛЕГКО определять НАПРАВЛЕНИЕ ЛИНИЙ МАГНИТНОГО ПОЛЯ??Скачать

Электрическое поле. Напряженность электрического поля. Силовые линии электрического поля. 10 класс.Скачать

4. Построение эпюр в раме ( практический курс по сопромату )Скачать

Определяем реакции опор рамыСкачать

Сопромат. Часть 1. Растяжение (сжатие). Построение эпюр продольных сил и нормальных напряжений.Скачать

Урок 93. Основное уравнение динамики вращательного движенияСкачать

Термех. Статика. Расчётно-графическая работа по статике №2. Задание 1 и решениеСкачать

Статически определимая рама. Эпюры внутренних сил. Часть 1Скачать