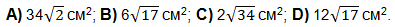Сечением тетраэдра могут быть треугольник четырехугольник пятиугольник (3 видео)

Какие многоугольники могут получиться в сечении тетраэдра, параллелепипеда? Вопрос №16 к 1 главе, Геометрия, 10-11 класс, Атанасян Л.С.

Последний вопрос главы.

Какие многоугольники могут получиться в сечении: а) тетраэдра; б) параллелепипеда?

Ловите!
а) Треугольники и 4-угольники; б) 3-, 4-, 5-, 6-угольники.

Привет. Запуталась при решении, нужна помощь знатоков.

Три прямые, проходящие через одну точку и не лежащие в одной ( Подробнее. )

Содержание

Методы построения сечений многогранников
СТЕРЕОМЕТРИЧЕСКИЕ ЗАДАЧИ НА ПОСТРОЕНИЕ СЕЧЕНИЙ МНОГОГРАННИКОВ И МЕТОДИКА ИХ ИСПОЛЬЗОВАНИЯ НА УРОКАХ В 10-11 КЛАССАХ.
(система уроков и факультативных занятий по теме “Построение сечений многогранников”)
Г10(I)-4. Тетраэдр и параллелепипед
🔥 Видео

Видео:Геометрия 10 класс (Урок№7 - Тетраэдр и параллелепипед.)Скачать

Методы построения сечений многогранников

Разделы: Математика

Метод сечений многогранников в стереометрии используется в задачах на построение. В его основе лежит умение строить сечение многогранника и определять вид сечения.

Данный материал характеризуется следующим особенностями:

Метод сечений применяется только для многогранников, так как различные сложные (наклонные) виды сечений тел вращения не входят в программу средней школы.
В задачах используются в основном простейшие многогранники.
Задачи представлены в основном без числовых данных, чтобы создать возможность их многовариантного использования.

Чтобы решить задачу построения сечения многогранника ученик должен знать:

что значит построить сечение многогранника плоскостью;
как могут располагаться относительно друг друга многогранник и плоскость;
как задается плоскость;
когда задача на построение сечения многогранника плоскостью считается решенной.

Поскольку плоскость определяется:

тремя точками;
прямой и точкой;
двумя параллельными прямыми;
двумя пересекающимися прямыми,

построение плоскости сечения проходит в зависимости от задания этой плоскости. Поэтому все способы построения сечений многогранников можно разделить на методы.

Существует три основных метода построения сечений многогранников:

Метод следов.
Метод вспомогательных сечений.
Комбинированный метод.

Первые два метода являются разновидностями Аксиоматического метода построения сечений.

Можно также выделить следующие методы построения сечений многогранников:

построение сечения многогранника плоскостью, проходящей через заданную точку параллельно заданной плоскости;
построение сечения, проходящего через заданную прямую параллельно другой заданной прямой;
построение сечения, проходящего через заданную точку параллельно двум заданным скрещивающимся прямым;
построение сечения многогранника плоскостью, проходящей через заданную прямую перпендикулярно заданной плоскости;
построение сечения многогранника плоскостью, проходящей через заданную точку перпендикулярно заданной прямой.

В федеральный перечень учебников по геометрии для 10-11 класов входят учебники авторов:

Атанасяна Л.С., Бутузова В.Ф., Кадомцева С.Б. и др (Геометрия, 10-11);
Погорелова А.В. (Геометрия, 7-11);
Александрова А.Д., Вернера А.Л., Рыжик В.И. (Геометрия, 10-11);
Смирновой И.М. (Геометрия, 10-11);
Шарыгина И.Ф. (Геометрия, 10-11).

Рассмотрим подробнее учебники Л.С, Атанасяна и Погорелова А.В.

В учебнике Л.С. Атанасяна на тему “Построение сечений многогранников” выделено два часа. В 10 классе в теме “Параллельность прямых и плоскостей” после изучения тетраэдра и параллелепипеда отводится один час на изложение параграфа “Задачи на построение сечений”. Рассматриваются сечения тетраэдра и параллелепипеда. И тема “Параллельность прямых и плоскостей” завершается решением задач на одном или двух часах (всего задач на построение сечений в учебнике восемь).

В учебнике Погорелова А.В. на построение сечений отводится около трех часов в главе “Многогранники”: один – на изучение темы “Изображение призмы и построение ее сечений”, второй – на изучение темы “Построение пирамиды и ее плоских сечений” и третий – на решение задач. В списке задач, приведенных после темы, задач на сечение насчитывается всего около десяти.

Мы предлагаем систему уроков по теме “Построение сечений многогранников” для учебника Погорелова А.В.

Материал предлагается расположить в той последовательности, в какой он может применяться для обучения учащихся. Из изложения темы “Многогранники” предлагается исключить следующие параграфы: “Построение сечений призмы” и “Построение сечений пирамиды” с тем, чтобы систематизировать данный материал в конце этой темы “Многогранники”. Классифицировать его по тематике задач с примерным соблюдением принципа “от простого к сложному” можно весьма условно следующим образом:

Определение сечения многогранников.
Построение сечений призмы, параллелепипеда, пирамиды методом следов. (Как правило в школьном курсе стереометрии используются задачи на построение сечений многогранников, решаемые основными методами. Остальные методы, в связи с их более высоким уровнем сложности, учитель может оставить для рассмотрения на факультативных занятиях или на самостоятельное изучение. В задачах на построение основными методами требуется построить плоскость сечения, проходящую через три точки).
Нахождение площади сечений в многогранниках (без использования теоремы о площади ортогональной проекции многоугольника).
Нахождение площади сечений в многогранниках (с применением теоремы о площади ортогональной проекции многоугольника).

СТЕРЕОМЕТРИЧЕСКИЕ ЗАДАЧИ НА ПОСТРОЕНИЕ СЕЧЕНИЙ МНОГОГРАННИКОВ И МЕТОДИКА ИХ ИСПОЛЬЗОВАНИЯ НА УРОКАХ В 10-11 КЛАССАХ.

(система уроков и факультативных занятий по теме “Построение сечений многогранников”)

Тема урока: “Построение сечений многогранников”.

Цель урока: ознакомление с методами построений сечений многогранников.

Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Г10(I)-4. Тетраэдр и параллелепипед

Геометрия 10 класс. Глава I. Тест 4.

Вариант 1.

1. Выбрать верные утверждения.

1) Грани тетраэдра – это треугольники, из которых состоит тетраэдр.

3) Диагональю параллелепипеда называется отрезок, соединяющий две вершины любой грани.

4) Сечением тетраэдра могут быть только треугольники и четырёхугольники, так как тетраэдр имеет 4 грани.

5) Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.

A) 1; 3; 4; B) 1; 2; 3; C) 1; 3; 5; D) 1; 4; 5.

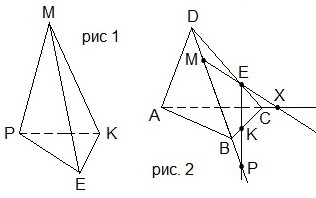
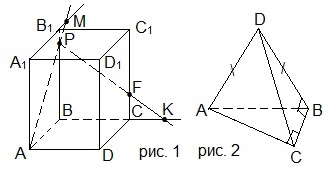
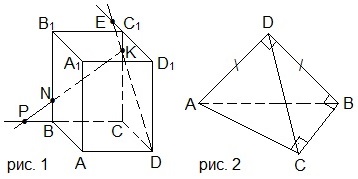
2. Назвать все пары скрещивающихся рёбер тетраэдра MPEK на рисунке 1.

A) MP и KE; MK и PE; ME и PK; B) MP и PE; MK и PE; ME и PK;

C) MP и KE; MK и KE; ME и PK; D) MP и KE; MK и PE; ME и EK.

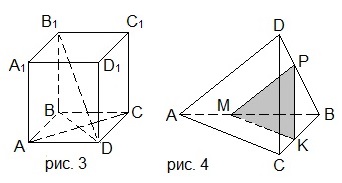
3. Выбрать верные утверждения, используя рисунок 2.

1) Х – точка пересечения прямой МЕ и плоскости АВС.

2) Р – точка пересечения прямой ЕК и плоскости АВD.

3) Точки Х и Р лежат в одной плоскости.

A) 2 и 3; B) 1 и 3; C) 1 и 2; D) 1; 2 и 3.

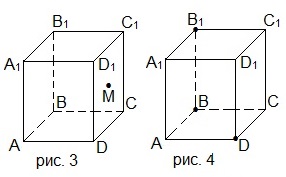
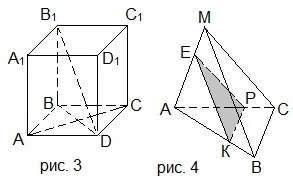
4. На рисунке 3 точка М принадлежит боковой грани CC₁D₁D прямоугольного параллелепипеда ABCDA₁B₁C₁D₁. Через точку М проведите сечение параллелепипеда плоскостью, параллельной плоскости АВС. Найдите площадь этого сечения, если АВ=5 см, AD=7 см, AA₁=9 см.

A) 45 см 2 ; B) 35 см 2 ; C) 63 см 2 ; D) 21 см 2 .

5. Основанием параллелепипеда ABCDA₁B₁C₁D₁ на рисунке 4 является квадрат со стороной 10 см и боковым ребром, равным 12 см. Угол B₁BD – прямой. Проведите сечение параллелепипеда через точки B, D и В₁ и найдите площадь этого сечения.

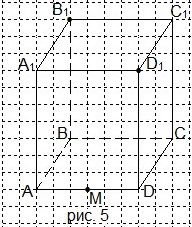
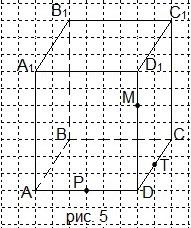
6. Перечертите рисунок 5 в тетрадь и проведите сечение параллелепипеда через точки B₁, D₁ и М. Какая фигура получилась в сечении?

A) треугольник; B) четырёхугольник; C) пятиугольник; D) шестиугольник.

Вариант 2.

1. Выбрать верные утверждения.

1) Поверхность, составленная из четырёх треугольников, называется тетраэдром.

2) Два ребра тетраэдра, не имеющие общих вершин, называют смежными.

3) Грани параллелепипеда – это параллелограммы, из которых составлен параллелепипед.

4) Секущей плоскостью параллелепипеда называют любую плоскость, по обе стороны от которой имеются точки данного параллелепипеда.

5) Две грани параллелепипеда, имеющие общие рёбра, называются противоположными.

A) 1; 3; 4; B) 1; 2; 3; C) 1; 3; 5; D) 1; 4; 5.

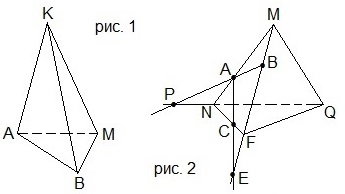
2. Назвать все пары скрещивающихся рёбер тетраэдра KABM на рисунке 1.

A) AK и AB; BK и AM; MK и AB; B) AK и BM; BK и AB; MK и AB;

C) AK и BM; BK и AM; MK и AB; D) AK и BM; BK и AM; MK и MB.

3. Выбрать верные утверждения, используя рисунок 2.

1) Р – точка пересечения прямой АВ и плоскости NMQ.

2) E – точка пересечения прямой AC и плоскости MFQ.

3) Точки E и Р лежат в различных плоскостях.

A) 1; 2 и 3; B) 1 и 3; C) 1 и 2; D) 2 и 3.

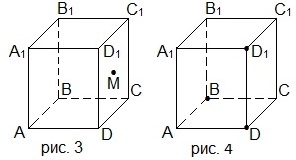
4. На рисунке 3 точка М принадлежит боковой грани CC₁D₁D прямоугольного параллелепипеда ABCDA₁B₁C₁D₁. Через точку М проведите сечение параллелепипеда плоскостью, параллельной плоскости АА₁D₁. Найдите площадь этого сечения, если АВ=5 см, AD=7 см, AA₁=9 см.

A) 45 см 2 ; B) 35 см 2 ; C) 63 см 2 ; D) 21 см 2 .

5. Основанием параллелепипеда ABCDA₁B₁C₁D₁ на рисунке 4 является квадрат со стороной 8 см и боковым ребром, равным 7 см. Угол B₁BD – прямой. Проведите сечение параллелепипеда через точки B, D и D₁ и найдите площадь этого сечения.

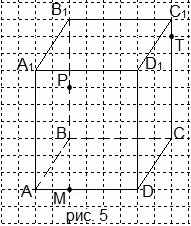
6. Перечертите рисунок 5 в тетрадь и проведите сечение параллелепипеда через точки М, Р и Т. Какая фигура получилась в сечении?

A) треугольник; B) четырёхугольник; C) пятиугольник; D) шестиугольник.

Вариант 3.

1. Выбрать верные утверждения.

1) Тетраэдр имеет 4 грани, 6 рёбер и 4 вершины.

2) Параллелепипед имеет 6 граней, 12 рёбер и 8 вершин.

3) Противоположные грани параллелепипеда параллельны и равны.

4) Секущей плоскостью тетраэдра называют любую плоскость, по одну сторону от которой имеются точки данного тетраэдра.

5) Секущая плоскость пересекает грани параллелепипеда по отрезкам-рёбрам параллелепипеда. Многоугольник, сторонами которого являются эти отрезки, называется сечением параллелепипеда.

A) 1; 3; 4; B) 1; 2; 3; C) 1; 3; 5; D) 1; 4; 5.

2. Выбрать верные утверждения, используя рисунок 1.

1) M – точка пересечения прямой АP и плоскости A₁B₁C₁.

2) K – точка пересечения прямой PF и плоскости ABD.

3) Точки M и K лежат в одной плоскости.

A) 1; 2 и 3; B) 1 и 3; C) 2 и 3; D) 1 и 2.

3. В тетраэдре DABC на рисунке 2 угол ADB равен 60°, углы АСВ и CBD прямые, AD=BD, АВ=26, DC=31. Найти АС. В ответе записать квадрат получившегося значения.

A) 391; B) 625; C) 380; D) 576.

4. Основанием параллелепипеда ABCDA₁B₁C₁D₁ на рисунке 3 является квадрат со стороной 4 см и боковым ребром, равным 6 см. Угол B₁BD – прямой. Проведите сечение параллелепипеда через прямую АС параллельно B₁D и найдите площадь этого сечения.

5. В тетраэдре МАВС на рисунке 4 проведено сечение КЕР параллельно грани ВСМ. Площадь треугольника ВСМ равна 60 см 2 . Найти площадь треугольника КЕР, если АК:КВ=7:3.

A) 29,4 см 2 ; B) 58,8 см 2 ; C) 294 см 2 ; D) 30,4 см 2 .

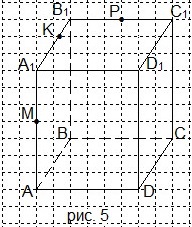
6. Перечертите рисунок 5 в тетрадь и проведите сечение параллелепипеда через точки М, Р и Т. Какая фигура получилась в сечении? A) треугольник; B) четырёхугольник; C) пятиугольник; D) шестиугольник.

Вариант 4.

1. Выбрать верные утверждения.

1) Две грани параллелепипеда, имеющие общее ребро, называются смежными.

2) Все рёбра параллелепипеда называются боковыми рёбрами.

3) Секущая плоскость пересекает грани тетраэдра по отрезкам прямых, содержащих рёбра тетраэдра. Многоугольник, сторонами которого являются эти отрезки, называется сечением тетраэдра.

4) Сечением параллелепипеда могут быть треугольники, четырёхугольники, пятиугольники и шестиугольники, так как параллелепипеда имеет 6 граней.

5) Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.

A) 1; 3; 4; B) 1; 2; 3; C) 1; 3; 5; D) 1; 4; 5.

2. Выбрать верные утверждения, используя рисунок 1.

1) Р – точка пересечения прямой NK и плоскости ACD.

2) E – точка пересечения прямой DK и плоскости A₁B₁C₁.

3) Точки E и Р лежат в различных плоскостях.

A) 2 и 3; B) 1 и 3; C) 1; 2 и 3; D) 1 и 2.

3. В тетраэдре DABC на рисунке 2 углы АСВ, АDВ и CBD — прямые, AD=BD=8, DC=11. Найти АС. В ответе записать квадрат получившегося значения.

A) 72; B) 71; C) 57; D) 64.

4. Основанием параллелепипеда ABCDA₁B₁C₁D₁ на рисунке 3 является квадрат со стороной 6 см и боковым ребром, равным 8 см. Угол B₁BD – прямой. Проведите сечение параллелепипеда через прямую АС параллельно B₁D и найдите площадь этого сечения.

5. В тетраэдре DАВС на рисунке 4 проведено сечение MPK параллельно грани АDС. Площадь треугольника МРК равна 4 см 2 . Найти площадь треугольника АDС, если СК:ВК=3:5.

A) 10,24 см 2 ; B) 20,48 см 2 ; C) 6,4 см 2 ; D) 8,64 см 2 .

6. Перечертите рисунок 5 в тетрадь и проведите сечение параллелепипеда через точки М, Р и К. Какая фигура получилась в сечении? A) треугольник; B) четырёхугольник; C) пятиугольник; D) шестиугольник.

1) Поверхность, составленная из четырёх треугольников, называется тетраэдром.

2) Грани тетраэдра – это треугольники, из которых состоит тетраэдр.

3) Тетраэдр имеет 4 грани, 6 рёбер и 4 вершины.

4) Два ребра тетраэдра, не имеющие общих вершин, называют противоположными.

6) Грани параллелепипеда – это параллелограммы, из которых составлен параллелепипед.

7) Параллелепипед имеет 6 граней, 12 рёбер и 8 вершин.

8) Две грани параллелепипеда, имеющие общее ребро, называются смежными.

9) Две грани параллелепипеда, не имеющие общих рёбер, называются противоположными.

10) Диагональю параллелепипеда называется отрезок, соединяющий две вершины, не принадлежащие одной грани.

11) Рёбра параллелепипеда, не принадлежащие основаниям, называются боковыми рёбрами.

12) Противоположные грани параллелепипеда параллельны и равны.

13) Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.

14) Секущей плоскостью тетраэдра называют любую плоскость, по обе стороны от которой имеются точки данного тетраэдра.

15) Секущей плоскостью параллелепипеда называют любую плоскость, по обе стороны от которой имеются точки данного параллелепипеда.

16) Секущая плоскость пересекает грани тетраэдра по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением тетраэдра.

17) Секущая плоскость пересекает грани параллелепипеда по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением параллелепипеда.

18) Сечением тетраэдра могут быть только треугольники и четырёхугольники, так как тетраэдр имеет 4 грани.

19) Сечением параллелепипеда могут быть треугольники, четырёхугольники, пятиугольники и шестиугольники, так как параллелепипеда имеет 6 граней.