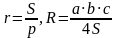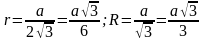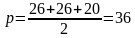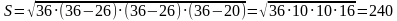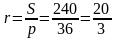Боковая сторона равнобедренного треугольника равна 4. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника.
Воспользуемся теоремой косинусов:
(здесь a и b — боковые стороны равнобедренного треугольника, c — основание.
Диаметр описанной окружности найдем по обобщенной теореме синусов:
Вместо того, чтобы искать основание треугольника, можно было найти угол при основании. Действительно, сумма углов при основании данного равнобедренного треугольника равна 60°. Эти углы равны, поэтому каждый из них равен 30°. Применяя обобщенную теорему синусов для боковой стороны и противолежащего ей угла, получаем:
Приведем решение Андрея Ларионова.
Угол при основании равен
Следовательно, дуга описанной окружности, на которую он опирается, равна 2 · 30° = 60°. Эту дугу стягивает боковая сторона треугольника.
Хорда, стягивающая дугу в 60°, равна радиусу окружности, поэтому радиус описанной окружности равен боковой стороне треугольника, тогда D = 2 · 4 = 8.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Решение задач по теме «Вписанная и описанная окружности»
Урок №7. СКАЧИВАЙТЕ файл на устройства, чтобы все знаки и формулы были видны и распознаны. Во время чтения файла онлайн происходит потеря формул.
Просмотр содержимого документа
«Решение задач по теме «Вписанная и описанная окружности»»
Тема: Решение задач по теме «Вписанная и описанная окружности»
Задачи: продолжить формирование навыков решения задач по теме.
Центр вписанной в треугольник окружности находится в точке пересечения его биссектрис.
Центр описанной около треугольника окружности находится в точке пересечения серединных перпендикуляров.
Формулы нахождения радиуса вписанной r и описанной R около треугольника окружностей.
Для любого треугольника:
Для равностороннего треугольника.
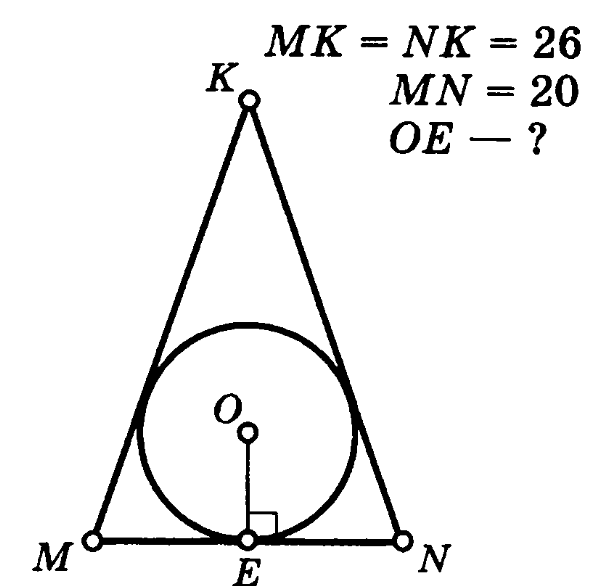
Задача 1. В равнобедренном треугольнике MKN боковые стороны равны 26, а основание – 20. В треугольник вписана окружность с радиусом ОЕ. Найти длину ОЕ.
Решение (краткое). Радиус окружности, вписанной в равнобедренный треугольник можно вычислить по стандартной формуле 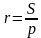
Ответ: 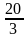
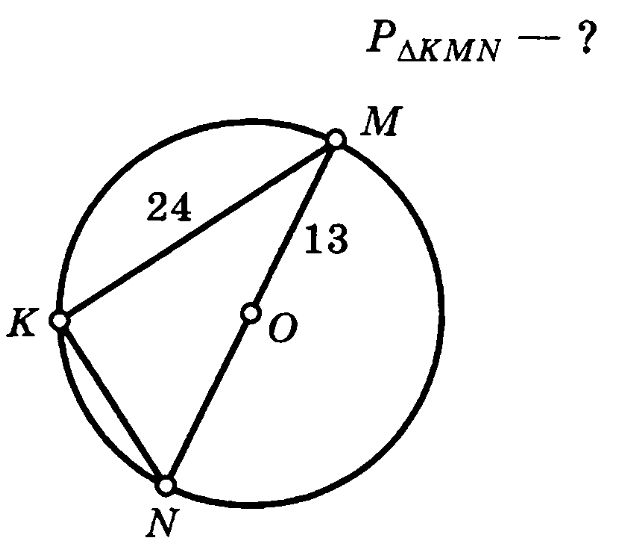
Задача 2. Прямоугольный треугольник KMN описан около окружности радиуса 13. Один из катетов треугольника равен 24. Найти периметр треугольника.
Решение (краткое). MN=d=2r=26, по теореме Пифагора KN=10, Р=60.
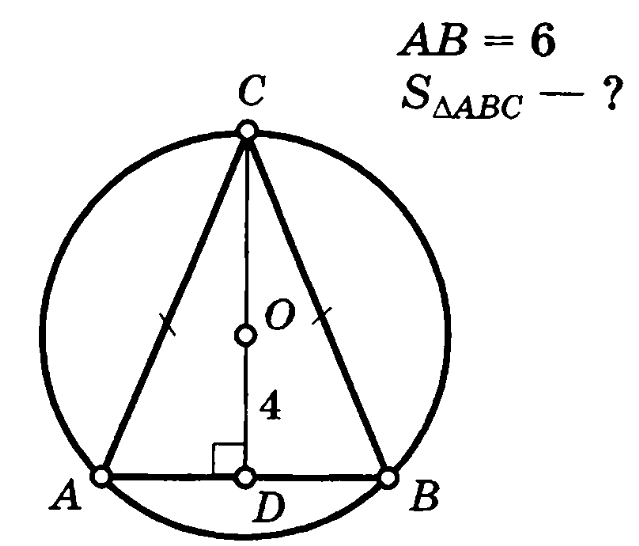
Задача 3. Равнобедренный треугольник АВС вписан в окружность, отрезок ОD=4. Найти площадь треугольника.
Решение (краткое). ОВ=5, ОС=ОВ=5, СD=9, S=0.5*9*6=27.
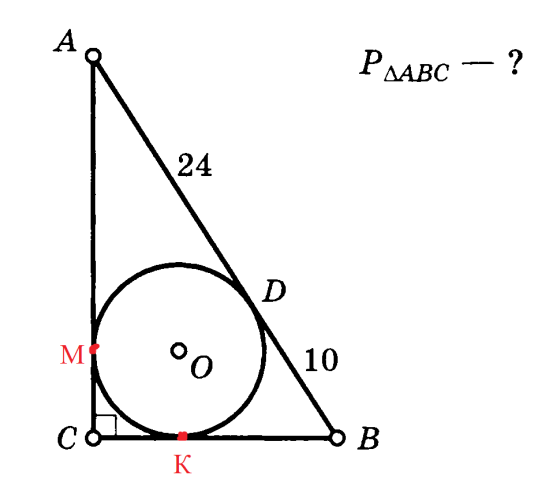
Задача 4. Прямоугольный треугольник описан около окружности. Точка D делит гипотенузу на две части, длинами по 10 и 24. Найти периметр треугольника.
Решение (краткое). DB=DK=10, AD=AM=24.
KOMC – квадрат, т.к. ОК перпендикулярен СВ, ОМ перпендикулярен АС и KC=CM, OK=OM=r.
Пусть KC=CM=х, тогда ВС=10+х, АС=24+х, АВ=24+10=34.
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

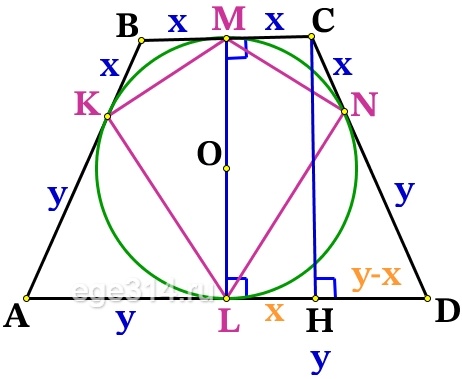
Решение №2583 Около окружности с центром О описана трапеция ABCD с основаниями AD и ВС.
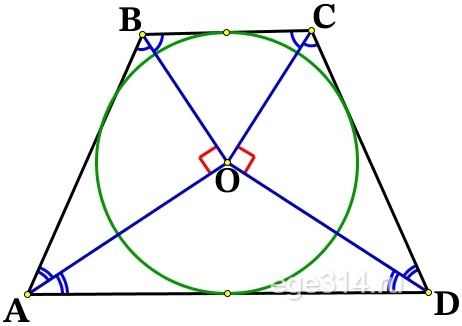
Около окружности с центром О описана трапеция ABCD с основаниями AD и ВС.
а) Докажите, что треугольник АОВ прямоугольный.
б) Найдите отношение большего основания трапеции к меньшему, если известно, что АВ = CD, а площадь четырёхугольника с вершинами в точках касания окружности со сторонами трапеции составляет frac площади трапеции ABCD.
Источник: Ященко ЕГЭ 2022 (36 вар)
а) Доказать , что в ΔАОВ ∠АОВ = 90° (тогда он прямоугольный) .
Окружность вписана в углы: ∠ВAD, ∠ADC, ∠DCB и ∠CBA. Центр окружности, которая вписана в угол, расположен на биссектрисе этого угла, значит АО, DO, СО, ВО – биссектрисы и делят соответствующие углы пополам.
∠ВAD + ∠CBA = 180°
∠ADC + ∠DCB = 180°
Как односторонние углы, при параллельных прямых AD||ВС (основания трапеции) и секущих AB и СD соответственно.
Зная о биссектрисах поделим всё на 2:
Рассмотрим треугольники ΔАВО и ΔDCO, сумма углов любого треугольника равна 180°, тогда:
∠AOB = ∠COD = 90°
Что и требовалось доказать.
б) Найти: frac , если АВ = СD, S_=fraccdot S_ :
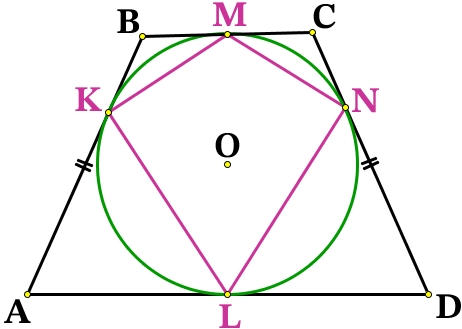
Отрезки касательных к окружности, проведённые из одной точки, равны:
BM = BK
CM = CN
AK = AL
DL = DN
Т.к. AB = CD, то:
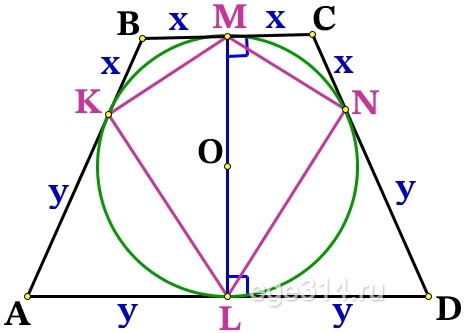
BK = СN = BM = CM = x
AK = DN = AL = DL = y
Проведём радиусы из точки О к касательным ВС и AD, тогда ОМ⊥ВС, OL⊥AD, точка О∈OM, O∈OL, значит МL это одна прямая и высота трапеции:
Проведём ещё одну высоту трапеции СН:
MC = LH, МCHL – прямоугольник, значит MC = LH = x , найдём HD:
HD = LD – LH = y – x
Из прямоугольного ΔСHD по теореме Пифагора найдём СН:
СН 2 + HD 2 = CD 2
CH 2 + (y – x) 2 = (y + x) 2
CH 2 = (y + x) 2 – (y – x) 2 = y 2 + 2xy + x 2 – y 2 + 2xy – x 2 = 4xy
CH=sqrt=2sqrt
Выразим площадь SABCD :
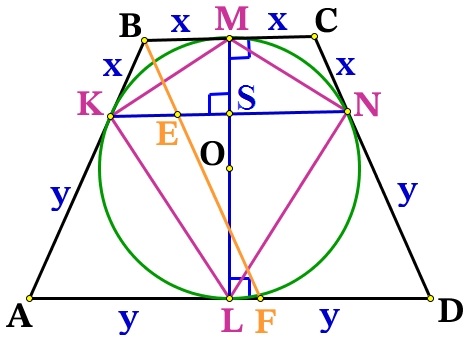
В четырёхугольнике проведём KMNL диагональ KN, прямые ВС и KN отсекают равные отрезки ВК = СN = x, значит они по теорема Фалеса параллельны ВС||KN, т.к. BC⊥LM, то KM⊥ML, значит угол между диагоналями ∠MSK = 90°.
Диагональ ML = 2sqrt , как высота трапеции.
Проведём BF||CD и пересекающая KN в точке Е. BCDF – параллелограмм, значит EN = BC = 2x.
ΔАВF подобен ΔВКЕ (∠В – общий, ∠ВКЕ = ∠ВАF – соответственные). Из пропорциональности сторон найдём КЕ:
Найдём диагональ KN:
Выразим площадь SKMNL :
S_=fraccdot MLcdot KNcdot sin angle MSK=fraccdot 2sqrtcdot fraccdot sin 90^=sqrtcdot fraccdot 1= frac<4xysqrt>
Подставим выраженные площади с исходное отношение:
Т.к. у нас у большее основание, а х меньшее, то их отношение равно 8.
🎦 Видео
Задача про трапецию, описанную около окружностиСкачать

Окружность. 7 класс.Скачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

9 класс, 22 урок, Окружность, описанная около правильного многоугольникаСкачать

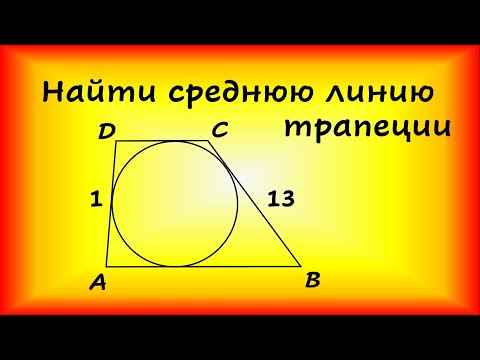
Боковые стороны трапеции, описанной около окружности, равны 13 и 1. Найдите среднюю линию трапеции.Скачать
ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать

Геометрия 7 класс (Урок№16 - Окружность. Задачи на построение.)Скачать

Вписанная и описанная окружность - от bezbotvyСкачать

Задача 6 №27916 ЕГЭ по математике. Урок 133Скачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Как решать задания на окружность ОГЭ 2021? / Разбор всех видов окружностей на ОГЭ по математикеСкачать

ЕГЭ математика 2023 Вариант 2 задача 1Скачать
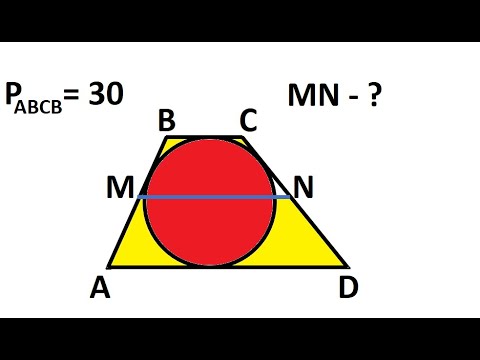
ОГЭ 2023. РАЗБОР ЗАДАНИЯ №16 "Окружность"Скачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Задача на окружности из ОГЭ-2023!! Разбор за 30 секСкачать

✓ Радиус описанной окружности | ЕГЭ. Задание 1. Математика. Профильный уровень | Борис ТрушинСкачать

Построить описанную окружность (Задача 1)Скачать