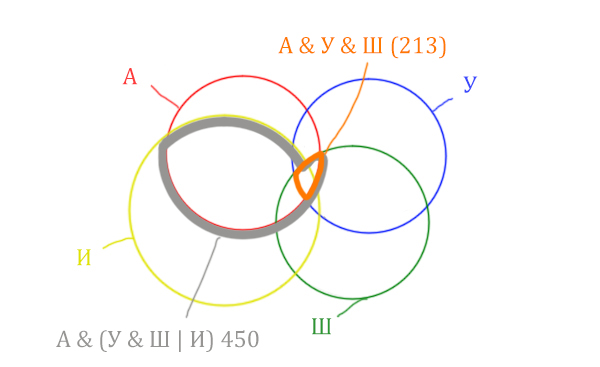Решение задач с окружностями информатика (3 видео)

Круги Эйлера в информатике

Сегодня разберём задачи на круги Эйлера в информатике.

Леонард Эйлер — швейцарский, немецкий и российский математик и механик, сыгравший огромную роль в развитии этих наук.

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
Пушкин	3500
Лермонтов	2000
Пушкин \| Лермонтов	4500

Какое количество страниц (в тысячах) будет найдено по запросу Пушкин & Лермонтов? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

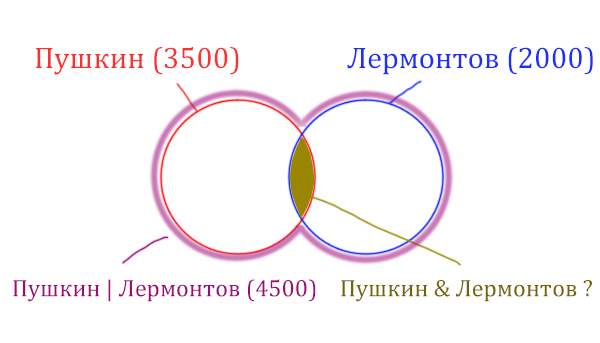
Видим, что по запросу «Пушкин» в поисковике нашлось 3500 страниц. По запросу «Лермонтов» — 2000 страниц.

Запрос «Пушкин | Лермонтов» обозначает, что поисковик выдаст страницы, где есть слова про «Пушкина», и страницы, где есть слова про «Лермонтова», а так же могут быть страницы, где написано и про «Пушкина», и про «Лермонтова» одновременно.

Если сложить страницы, в которых написано про «Пушкина» и про «Лермонтова» получается 3500 + 2000 = 5500 страниц. Но почему же при запросе «Пушкин | Лермонтов» получается меньше страниц, всего 4500 ?

Этот факт обозначает то, что когда мы подсчитывали страницы про «Пушкина» (3500 страниц), мы подсчитали и те страницы, где было написано и про «Пушкина», и про «Лермонтова» одновременно.

Тоже самое и для количества страниц, где написано про «Лермонтова» (2000 страниц). В этом числе находятся и те, в которых одновременно упоминается и про «Пушкина», и про «Лермонтова».

В вопросе спрашивается, сколько страниц будет по запросу «Пушкин & Лермонтов«. Это обозначает, что как раз нужно найти количество страниц, где будет одновременно написано и про «Пушкина», и про «Лермонтова».

Пушкин & Лермонтов = (3500 + 2000) — 4500 = 5500 — 4500 = 1000 страниц.

Это и будет ответ!

Содержание

Теперь решим эту задачу с помощью Кругов Эйлера!
Решение задач с окружностями информатика
«Разработка алгоритмов и программ для решения задач с геометрическим содержанием по теме «Окружность и круг» с учетом требований ФГОС» методическая разработка по информатике и икт (9 класс) на тему
Скачать:
Предварительный просмотр:
Введение
Основная часть
Задания, которые рассматриваются на занятии:
Проверяемые элементы содержания
Основное содержание теоретической части
Задания на этапе первичного закрепления
📺 Видео

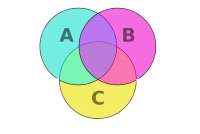
Теперь решим эту задачу с помощью Кругов Эйлера!

У нас всего есть две сущности: «Пушкин» и «Лермонтов». Поэтому рисуем два пересекающихся круга, желательно разными цветами.

Объединение двух кругов в общую фигуру ( показано фиолетовым цветом), показывает операцию «Пушкин | Лермонтов». Эта операция всегда стремится увеличить площадь, объединить площади других фигур!

Обратите внимание, что круги пересекаются, из-за этого сумма площадей двух кругов по отдельности (3500 + 2000 = 5500) больше чем у фигуры, которая характеризует логическую операцию «ИЛИ» «Пушкин | Лермонтов» (4500).

Нужно найти площадь фигуры Пушкин & Лермонтов, которая закрашена золотистым цветом. Данная логическая операция «И» стремится уменьшить площадь. Она обозначает общую площадь других фигур.

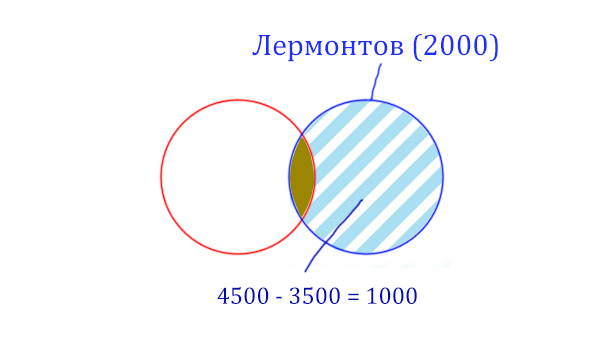
Найдём сначала заштрихованную часть синего круга. Она равна: площадь фиолетовой фигуры (4500) минус площадь красного круга (3500).

Теперь легко найти площадь золотистой фигуры. Для этого нужно от площади синего круга вычесть площадь заштрихованной части. Получается:

Пушкин & Лермонтов (Количество страниц) = 2000 — 1000 = 1000

Получается, что по запросу Пушкин & Лермонтов будет найдено 1000 страниц.

Рассмотрим ещё одну не сложную разминочную задачу.

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
Кокос \| Ананас	3400
Кокос & Ананас	900
Кокос	2100

Какое количество страниц (в тысячах) будет найдено по запросу Ананас?

Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

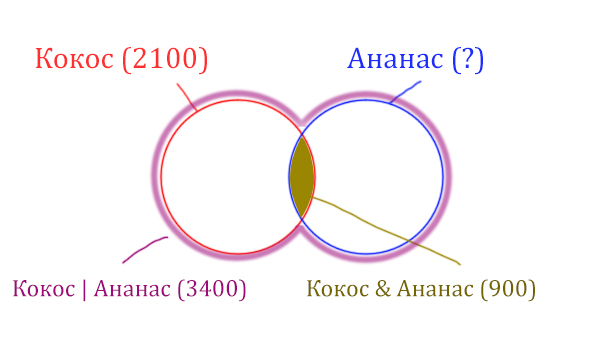
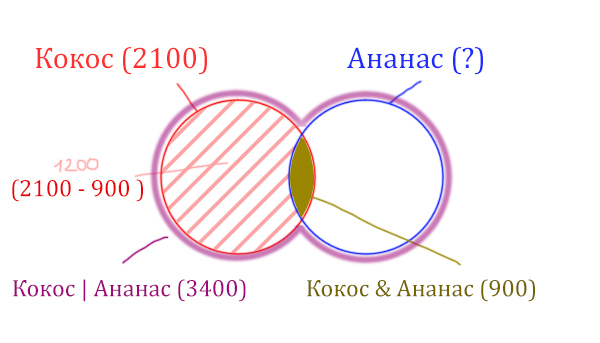
У нас две сущности: Кокос и Ананас. Нарисуем два круга Эйлера, которые пересекаются между собой. Так же отменим все имеющееся данные.

Найдём заштрихованную часть красного круга.

Весь красный круг 2100. Золотистая область равна 900. Заштрихованная часть равна 2100 — 900 = 1200.

После того, как нашли заштрихованную часть (такой полумесяц), можно найти уже площадь синего круга. Для этого нужно от площади фиолетовой фигуры отнять площадь заштрихованной части!

Ананас (Количество страниц) = 3400 — 1200 = 2200
Ответ: 2200

Разберём классическую задачу из информатики по кругам Эйлера.

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
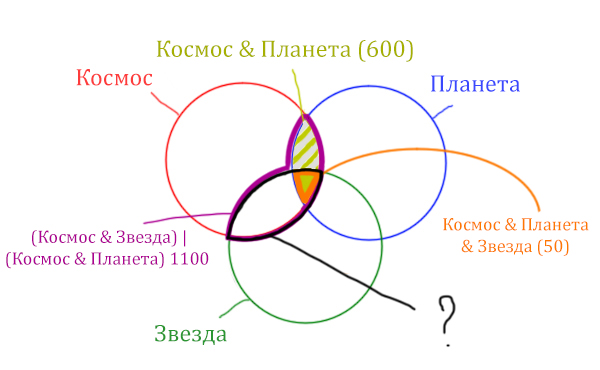
(Космос & Звезда) \| (Космос & Планета)	1100
Космос & Планета	600
Космос & Планета & Звезда	50

Какое количество страниц (в тыс.) будет найдено по запросу Космос & Звезда?

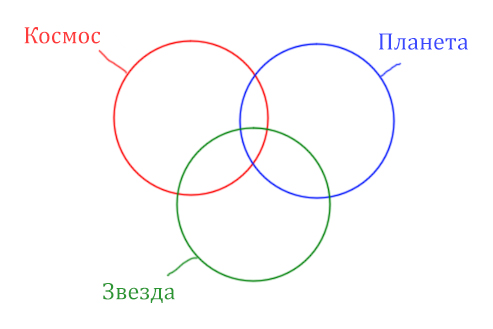
В этой задаче у нас три сущности: Космос, Планета, Звезда. Поэтому рисуем три круга Эйлера, которые пересекаются между собой.

Могут ли круги не пересекаться ? Могут! Если мы докажем, что площади по отдельности двух кругов в сумме дают площадь фигуры, которая получается при применении операции логического «ИЛИ».

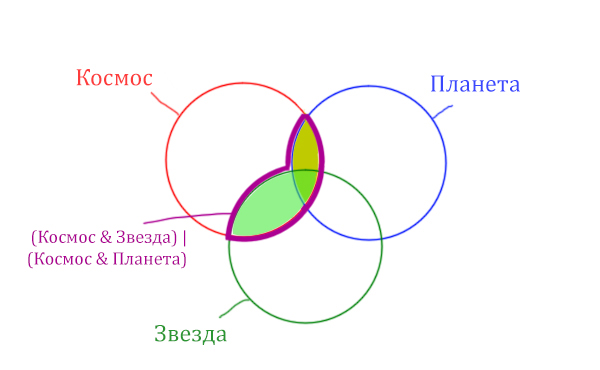
Теперь отметим на нашем рисунке запрос (Космос & Звезда) | (Космос & Планета).

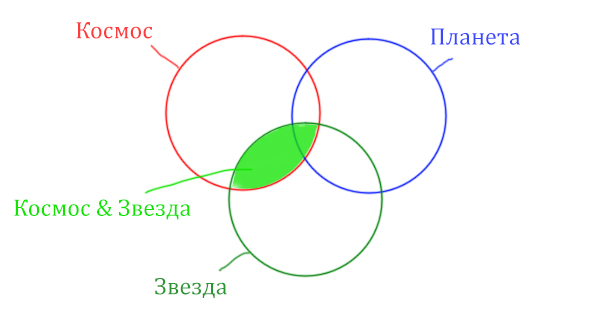
Сначала отменим для себя то, что находится в скобках. Первое Космос & Звезда

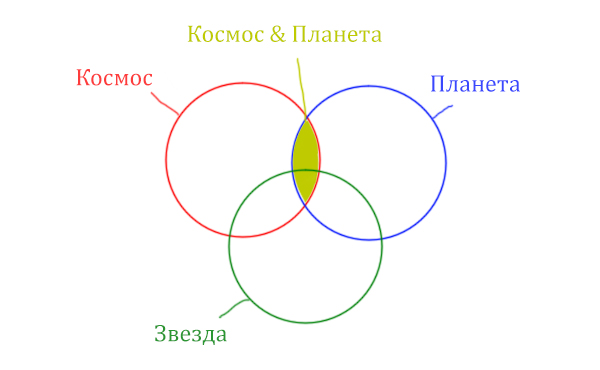
Теперь отметим вторую скобку Космос & Планета.

В выражении (Космос & Звезда) | (Космос & Планета) две скобки соединяет знак логического «ИЛИ». Значит, эти две области нужно объединить! Область (Космос & Звезда) | (Космос & Планета) отмечена фиолетовым цветом!

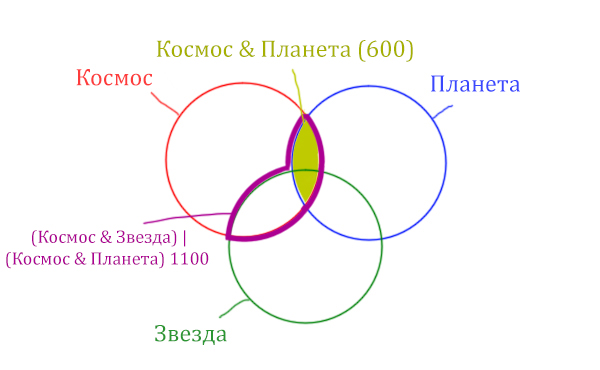
Отметим Космос & Планета ещё раз, т.к. для этого выражения известно количество страниц.

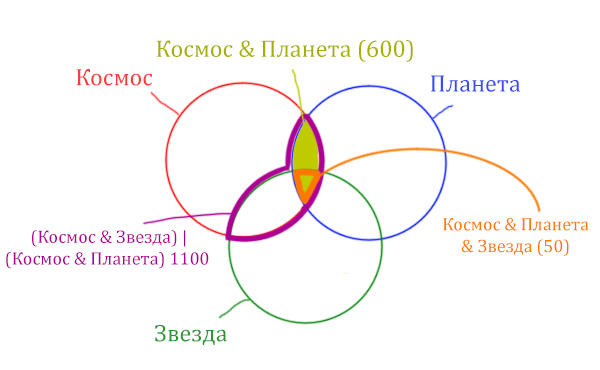
Площадь фигуры для выражения Космос & Планета & Звезда будет очень маленькая. Это общая часть для всех трёх кругов. Отметим её оранжевым цветом! Каждая точка этой фигуры должна одновременно быть в трёх кругах!

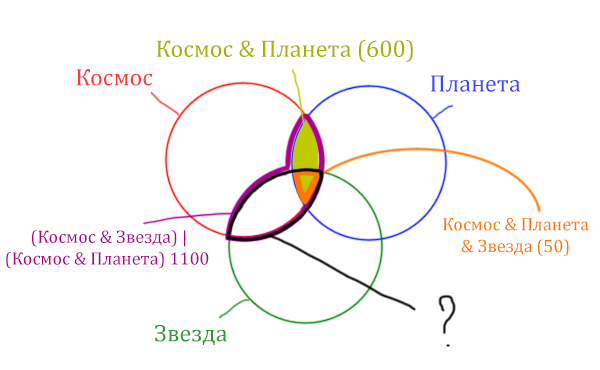
Найти нужно Космос & Звезда. Отменим на рисунке чёрным цветом ту область, которую нужно найти. Мы эту область уже отмечали салатовым цветом.

Теперь у нас есть все компоненты, чтобы решить эту задачу.

Найдём заштрихованную область.

Вся область Космос & Планета равна 600. А заштрихованная часть равна: область Космос & Планета (600) минус оранжевая область (50).

Количество страниц в заштрихованной части = 600 — 50 = 550

Тогда черная область легко находится: фиолетовая область (1100) минус заштрихованная область (550).

Количество страниц (при запросе Космос & Звезда) = 1100 — 550 = 550
Ответ: 550

Закрепляем материал по задачам на Круги Эйлера.

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
Море & Солнце	290
Море & Пляж	355
Море & (Пляж \| Солнце)	465

Какое количество страниц (в тысячах) будет найдено по запросу Море & Пляж & Солнце? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

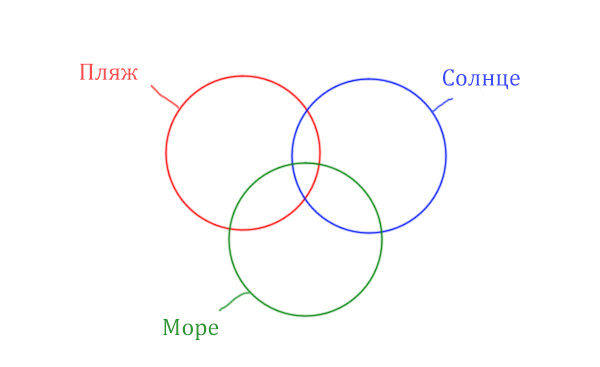
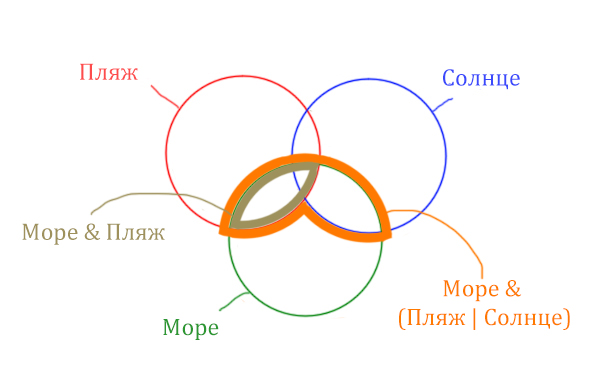
В задаче используются три сущности: Море, Пляж, Солнце. Поэтому нарисуем три пересекающихся круга Эйлера.

Отметим все области для которых нам даны количество страниц.

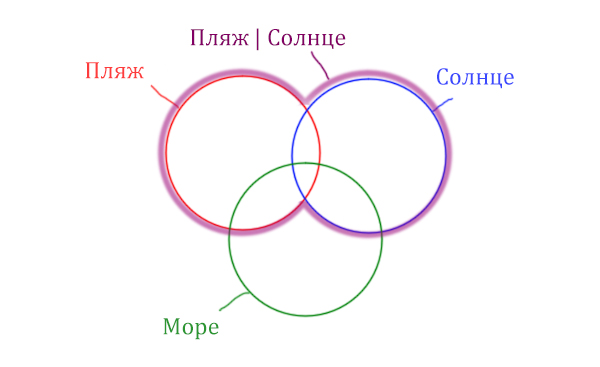
В начале отметим Море & (Пляж | Солнце). Для начало нарисуем область, которая в скобках (Пляж | Солнце)

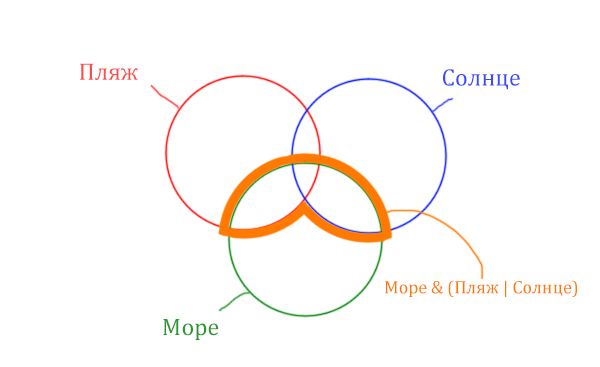
Теперь нужно очертить общую часть фиолетовой области и зелёного круга и получится Море & (Пляж | Солнце). Отметим оранжевым цветом.

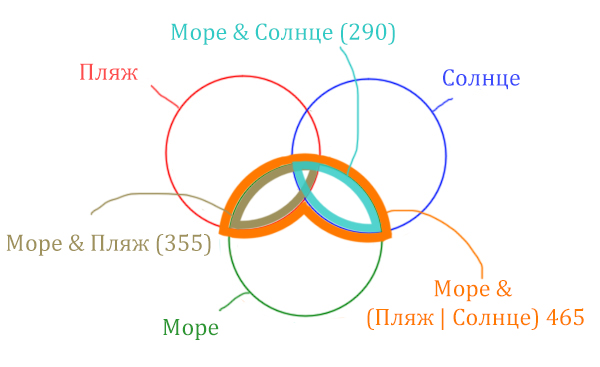
Теперь отметим Море & Пляж.

Теперь отметим Море & Солнце.

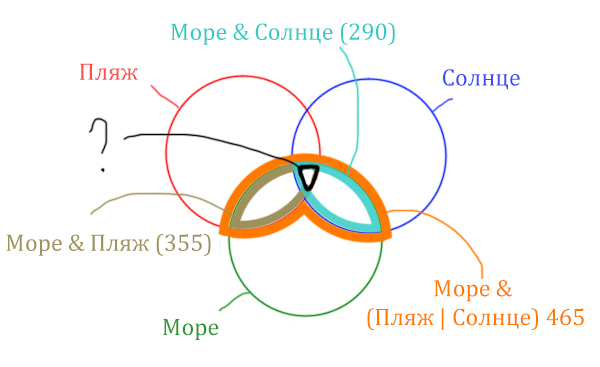
Найти нужно ту область, которая получается в результате выделения общей части для всех трёх кругов! Обозначим её чёрным цветом!

Найдём заштрихованную область!

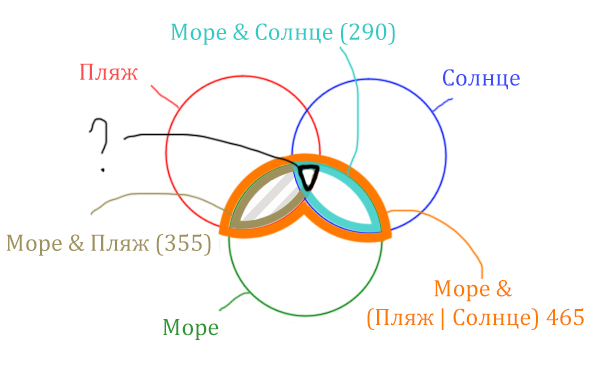
Количество страниц (в заштрихованной области) =
= Количество страниц (В оранжевой области) — Море & Солнце =
= 465 — 290 = 175

Чтобы найти искомую чёрную область, нужно из Море & Пляж (355) вычесть заштрихованную область (175).

Количество страниц (Море & Пляж & Солнце) =
= Море & Пляж (355) — Количество страниц (в заштрихованной области) 175 =
= 355 — 175 = 180
Ответ: 180

Решим ещё одну тренировочную задачу из информатики на Круги Эйлера.

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&».

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
Англия & (Уэльс & Шотландия \| Ирландия)	450
Англия & Уэльс & Шотландия	213
Англия & Уэльс & Шотландия & Ирландия	87

Какое количество страниц (в тысячах) будет найдено по запросу

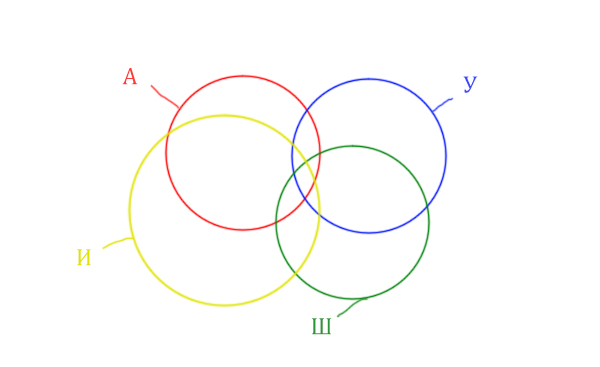
Нужно нарисовать 4 пересекающихся круга. Сначала нарисуем три круга, как обычно, оставив немного места для четвёртого круга.

Четвёртый круг для Ирландии нужно нарисовать так, чтобы он проходил через область (Англия & Уэльс & Шотландия). Это нам подсказывает сама таблица, где есть количество страниц для Англия & Уэльс & Шотландия, а так же для Англия & Уэльс & Шотландия & Ирландия.

Нужно отметить на рисунке Англия & (Уэльс & Шотландия | Ирландия). Это будем делать, как всегда поэтапно.

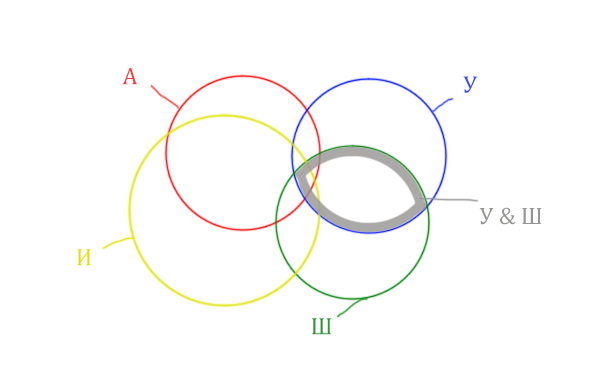
Область Уэльс & Шотландия выглядит так:

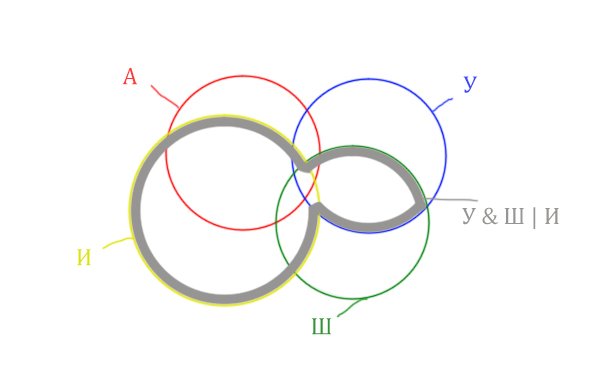
Добавим к этой области Ирландию через логическое «ИЛИ». Получается область (Уэльс & Шотландия | Ирландия). Произошло объединение серой области и жёлтого круга!

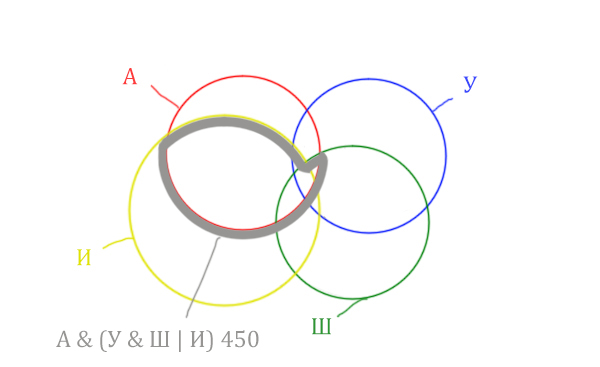
Теперь нужно сделать операцию логического «И» получившийся области с «Англией». Тогда область Англия & (Уэльс & Шотландия | Ирландия) примет вид:

Т.е. это общее между предыдущем серым контуром и красным кругом!

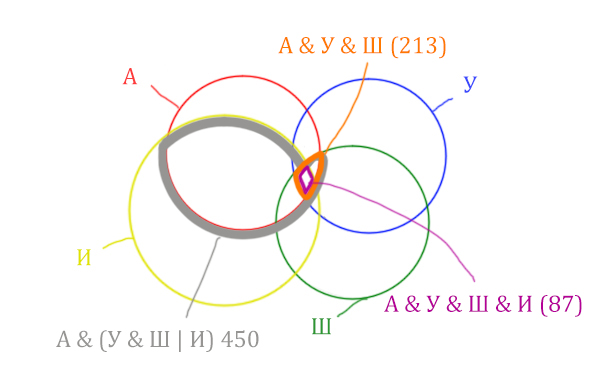
Отметим Англия & Уэльс & Шотландия — это общая территория трёх кругов: Красного, Синего и Зелёного. Отмечено оранжевым цветом.

Отметим Англия & Уэльс & Шотландия & Ирландия — это общая территория четырёх кругов. Область получается ещё меньше. Если взять точку в этой области, то мы будем находится сразу в четырёх кругах одновременно. Отмечено фиолетовым цветом.

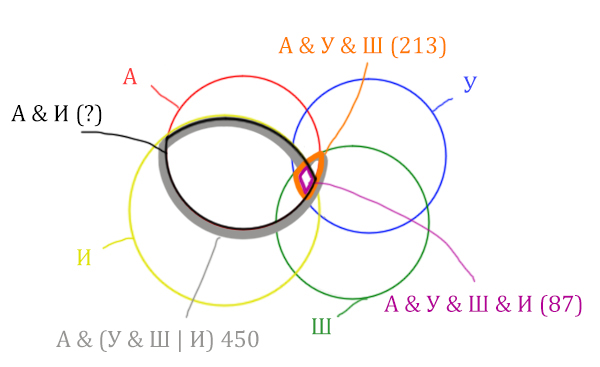
Отметим то, что нужно найти Англия & Ирландия чёрным цветом.

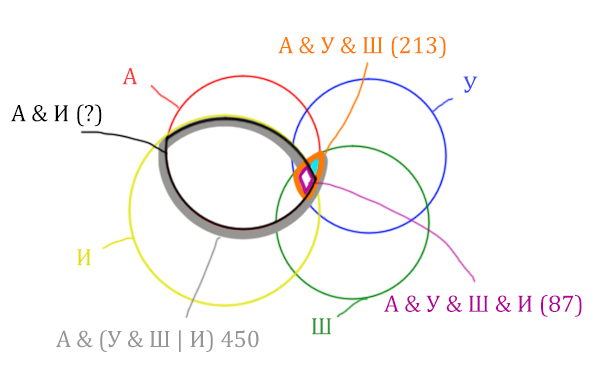
Искомую чёрную область легко найти, если из серой области вычесть кусочек, окрашенный в бирюзовый цвет!

Найдём, сколько страниц приходится на бирюзовый кусочек:

Количество страниц (для бирюзового кусочка) =
= Англия & Уэльс & Шотландия (213) — Англия & Уэльс & Шотландия & Ирландия (87) =
= 213 — 87 = 126

Найдём искомую чёрную область.

Количество станиц (для чёрной области) =
= Англия & (Уэльс & Шотландия | Ирландия) (450) — Количество (для бирюзового кусочка) =
450 — 126 = 324

Это и будет ответ!

Разберём задачу из реального экзамена по информатике, которая была в 2019 году в Москве! (Сейчас в 2021 задачи не встречаются на Круги Эйлера)

Задача (ЕГЭ по информатике, 2019, Москва)

В таблице приведены запросы и количество страниц, которые нашёл поисковый сервер по этим запросам в некоторым сегменте Интернета:

Запрос	Найдено страниц (в тысячах)
Суфле	450
Корзина	200
Эклер	490
Суфле & Корзина	70
Суфле & Эклер	160
Корзина & Эклер	0

Сколько страниц (в тысячах) будет найдено по запросу

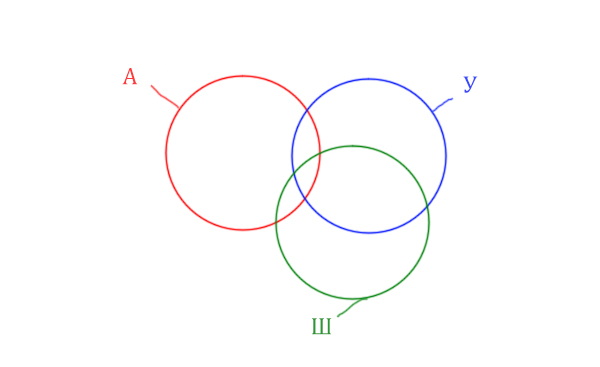
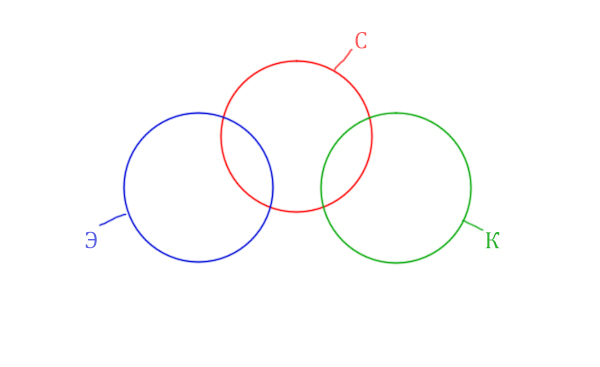
Видим, что у нас три поисковых разных слова, поэтому будет три разных круга Эйлера!

Так же видим, что логическое «И» между словами Корзина и Эклер даёт 0 страниц. Это значит, что эти круги не пересекаются! Так же круги бы не пересекались, если бы операция логического «ИЛИ» совпадала бы с суммой этих кругов.

Видим, что Суфле имеет с двумя кругами пересечения, а Корзина и Эклер не пересекаются.

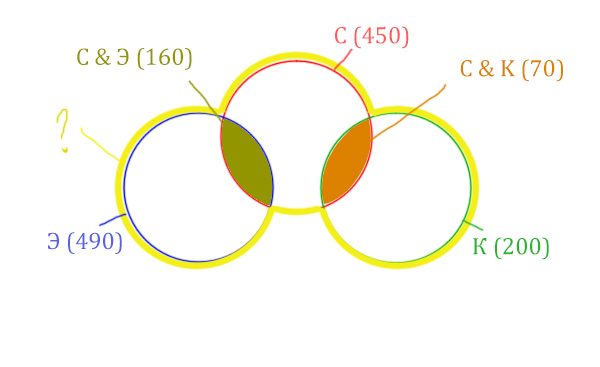
Отметим всё, что нам дано в условии.

Жёлтым цветом отмечено Суфле | Корзина | Эклер . Объединение всех трёх кругов. Это то, что нужно найти.

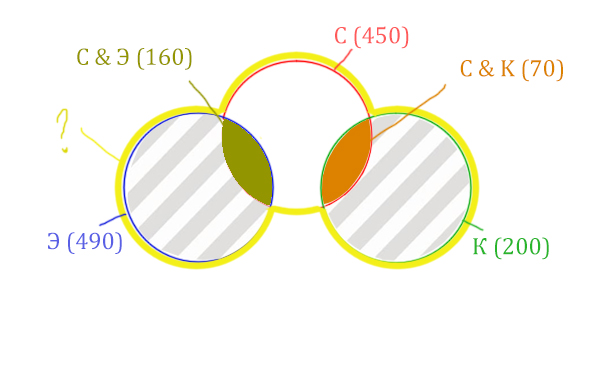
Искомая жёлтая фигура складывается из заштрихованных областей и красного круга! Площадь красного круга мы знаем. Нужно найти площади заштрихованных частей.

Левая заштрихованная область находится просто:

Количество страниц (лев. заштрих. область) =
= Эклер (490) — Суфле & Эклер (160) = 330

Так же найдём площадь правой заштрихованной области:

Количество страниц (прав. заштрих. область) =
= Корзина (200) — Суфле & Корзина (70) = 130

Теперь можно найти искомую жёлтую область

Количество страниц (Суфле | Корзина | Эклер) =
= Красный круг (450) + лев. заштрих. область (310) + прав. заштрих. область (130) =
= 450 + 330 + 130 = 910

Задача решена, можно писать ответ.

Разберём ещё одну задачу из реального ЕГЭ уже 2020 года

Задача (ЕГЭ по информатике, 2020, Москва)

Запрос	Найдено страниц (в тысячах)
Аврора	50
Крейсер	45
Заря	23
Аврора & Заря	9
Заря & Крейсер	0
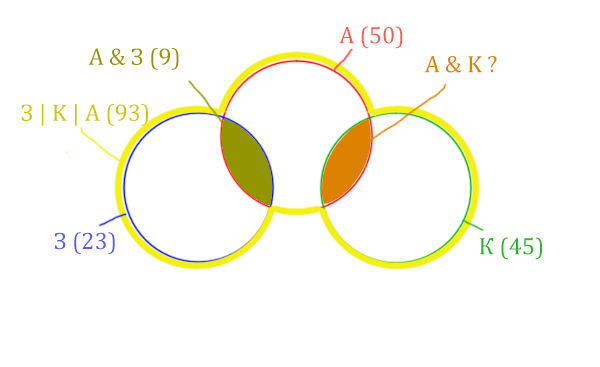
Заря \| Крейсер \| Аврора	93

Сколько страниц (в тысячах) будет найдено по запросу

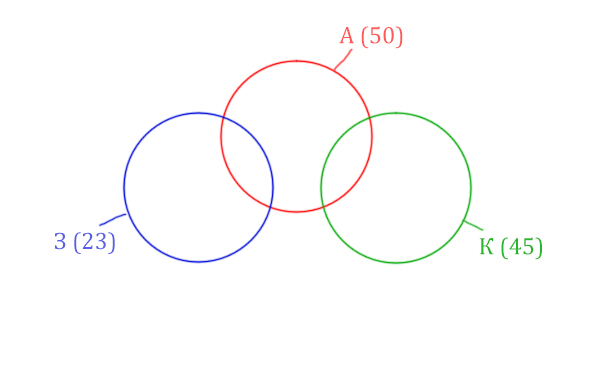
Количество страниц при запросе Заря & Крейсер равно нулю. Значит, эти два круга не будут пересекаться.

Нарисуем все данные на рисунке.

Нужно найти для начала заштрихованную правую часть.

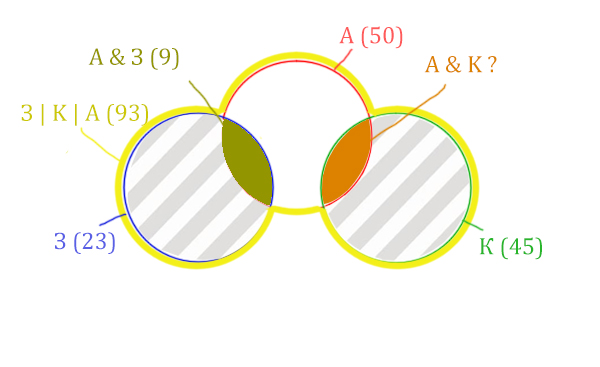
Количество страниц (для двух заштрих. частей) =
З | К | А (93) — Красный круг (50) = 43

Левую заштрихованную область легко найти.

Количество страниц (для левой заштрих. части) =
Синий круг (23) — А & З (9) = 14

Тогда для правой заштрихованной области получается:

Колич. страниц (для правой заштрих. части) =
Колич. страниц (для двух заштрих. частей) (43) — Колич. страниц (для лев. заштрих. части) (14) =
= 43 — 14 = 29

Тогда искомую область легко найти:

Колич. страниц (А & K) =
Зелёный круг (45) — Колич. страниц (для правой заштрих. части) (29) =
45 — 29 = 16
Ответ: 16

На этом всё! Надеюсь, вы теперь будете с удовольствием решать задачи по информатике с помощью Кругов Эйлера.

Видео:Решение задачи по теме "Информационный объём сообщения"Скачать

Решение задач с окружностями информатика

Требовалось написать программу, которая вводит с клавиатуры координаты точки на плоскости (x, y — действительные числа) и определяет принадлежность точки заштрихованной области, включая её границы. Программист торопился и написал программу неправильно.

Последовательно выполните следующее.

1. Перерисуйте и заполните таблицу, которая показывает, как работает программа при аргументах, принадлежащих различным областям (A, B, C, D, E, F, G и H).

Точки, лежащие на границах областей, отдельно не рассматривать. В столбцах условий укажите «да», если условие выполнится, «нет», если условие не выполнится, «—» (прочерк), если условие не будет проверяться, «не изв.», если программа ведет себя по-разному для разных значений, принадлежащих данной области. В столбце «Программа выведет» укажите, что программа выведет на экран. Если программа ничего не выводит, напишите «—» (прочерк). Если для разных значений, принадлежащих области, будут выведены разные тексты, напишите «не изв». В последнем столбце укажите «да» или «нет».

2. Укажите, как нужно доработать программу, чтобы не было случаев ее неправильной работы. (Это можно сделать несколькими способами, достаточно указать любой способ доработки исходной программы.)

Паскаль	Бейсик
Си++	Алгоритмический

Область

Условие 1

(x*x+y*y>=4)

Условие 2

(x>= –2)

Условие 3

(y =4)

Условие 2

(x>= –2)

Условие 3

(y if (x*x+y*y>=4) and (x>= –2) and (y =0) then

(могут быть и другие способы доработки).

Требовалось написать программу, которая вводит с клавиатуры координаты точки на плоскости (х, у — действительные числа) и определяет принадлежность точки заштрихованной области. Программист торопился и написал программу неправильно.

if x*x+y*y >= 4 then

IF x*x+y*y >= 4 THEN

если x*x+y*y >= 4 то

Последовательно выполните следующее:

Паскаль	Бейсик
Си++	Алгоритмический язык

Область

Условие 1

(x*x+y*y >= 4)

Условие 2

(у >= −2)

Условие 3

(у = 4)

Условие 2

(у >= −2)

Условие 3

(у if (х * х + у * у >= 4) and (у >= −2) and (у

Видео:Множества и круги Эйлера для 8 задания на ОГЭ по информатике 2024 | УмскулСкачать

«Разработка алгоритмов и программ для решения задач с геометрическим содержанием по теме «Окружность и круг» с учетом требований ФГОС»
методическая разработка по информатике и икт (9 класс) на тему

Занятие, на котором решаются геометрические задачи с использованием алгоритмики и программирования.

Практическая работа на тему

«Разработка алгоритмов и программ для решения задач с геометрическим содержанием по теме «Окружность и круг» с учетом требований ФГОС»

В данной разработке представлены задачи с геометрическим содержанием по теме «Окружность и круг» для 9 класса. Для этих задач разработаны алгоритмы и программы на псевдокоде и языке Паскаль. Предмет информатики и ИКТ можно рассматривать как метапредмет, позволяющий более глубоко развивать межпредметные связи учебных дисциплин в средней общеобразовательной школе.

Видео:Информатика 9 класс (Урок№5 - Решение задач на компьютере.)Скачать

Скачать:

Вложение	Размер
prakticheskoe_zanyatie_algoritmy_geom_zadachi_shirobokovagi.docx	566.42 КБ

Видео:ВСЕ ТИПЫ 8 задания | Информатика ОГЭ 2023 | УмскулСкачать

Предварительный просмотр:

учитель математики информатики

Видео:7 класс. Задачи на измерение информацииСкачать

Введение

Одна из главная задач ФГОС, которые призваны реализовать развивающий потенциал общего среднего образования — готовить своих учеников к жизни, обеспечить ребенку общекультурное, личностное и познавательное развитие, вооружить умением учиться. Перед выпускниками, вступающими в самостоятельную жизнь, встаёт проблема решать новые, неизвестные задачи, которые неизбежно встанут перед ними. Результат образования можно «измерить» умением успешно решать такие задачи.

В новых стандартах метапредметным результатам уделено особое внимание, поскольку именно они обеспечивают более качественную подготовку учащихся к самостоятельному решению проблем, с которыми встречается каждый человек на разных этапах своего жизненного пути в условиях быстро меняющегося общества. Предмет информатики и ИКТ можно рассматривать как метапредмет, позволяющий более глубоко развивать межпредметные связи учебных дисциплин в средней общеобразовательной школе. Программирование обучает методам мышления, общим подходам к постановке и решению задач. Поэтому выбрана тема занятия, на котором решаются геометрические задачи с использованием алгоритмики и программирования.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Основная часть

Тема занятия : Разработка алгоритмов и программ для решения задач с геометрическим содержанием по теме «Окружность и круг».

Видео:Информатика ЕГЭ. Поиск оптимального маршрута по таблицеСкачать

Задания, которые рассматриваются на занятии:

вычисление длины окружности по заданному радиусу;
нахождение площади круга, ограниченного окружностью заданного радиуса;
нахождение площади кольца по внутреннему и внешнему радиусам;
вычисление расстояния между двумя точками с заданными координатами;
найти площади сектора по радиусу и дуге;
определение минимального радиуса круга, в который попадают точки, заданные координатами на плоскости;

Для решения задач используем линейные структуры, ветвления и циклы.

Видео:Круги Эйлера. Логическая задача на множества. Иностранные языкиСкачать

Проверяемые элементы содержания

Формальное исполнение алгоритма, записанного на естественном языке или умение создавать линейный алгоритм для формального исполнителя с ограниченным набором команд.

Знание основных конструкций языка программирования, понятия переменной, оператора присваивания.

Умение исполнить алгоритм для конкретного исполнителя с фиксированным набором команд.

Анализ алгоритма, содержащего вспомогательные алгоритмы, цикл и ветвление.

Умение анализировать результат исполнения алгоритма.

Видео:Решаем ОГЭ по информатике на 4 за 10 минут | Информатика ОГЭ УмскулСкачать

Основное содержание теоретической части

Алгоритмы работы с величинами: константы, переменные, понятие типов данных, ввод и вывод данных.

Структура программы на языке Паскаль. Представление данных в программе. Правила записи основных операторов: присваивания, ввода, вывода, ветвления, циклов.

Этапы решения задачи с использованием программирования: постановка задачи, формализация, алгоритмизация, кодирование, отладка, тестирование.

Практика на компьютере: знакомство с системой программирования на языке Паскаль; ввод, трансляция и исполнение данной программы; разработка и исполнение линейных, ветвящихся и циклических программ.

Переменная, константа, операторы ввода/вывода, оператор присваивания, арифметические операции с переменными.

Создание с использованием свойств геометрических фигур математических моделей для решения задач практического характера и задач из смежных дисциплин (для данного занятия – конкретно геометрии), исследовать полученные модели и интерпретировать результат.

Задачи на применение линейных алгоритмических структур. В ходе решения задач повторяются формулы курса геометрии 9 класса: вычисление длины окружности, площади круга, площади кольца, площади сектора, расстояния между двумя точками на плоскости, заданных координатами (метод координат в курсе геометрии).

Видео:Как решать задания на окружность ОГЭ 2021? / Разбор всех видов окружностей на ОГЭ по математикеСкачать

Задания на этапе первичного закрепления

Рассмотрим подробно задачи геометрического содержания с постановкой, математической моделью, алгоритмом, программой на языке Паскаль и полученными результатами (скриншот).

Задача 1. Вычислить длину окружности по заданному радиусу.

Результат – найти длину окружности.
Исходные данные – радиус окружности.
Ограничения на результат – положительное число.
Ограничения на исходные данные – положительное число.

Математическая модель. Вычислить длину окружности по формуле

Описать переменные. Ввести данные.

Вычислить по формуле длины окружности C= 2*π*R.

Write( ‘Введите радиус окружности R= ‘ );

WriteLn( ‘Длина окружности С= ‘ ,C: 5 : 3 );

Скриншот программы с результатами решения

Вывод. Программа работоспособна. Проверим результат с помощью калькулятора, получим число 37, 57344814. Верно.

Задача 2. Известна длина окружности. Найти площадь круга, ограниченного этой окружностью.

Результат – площадь круга.
Исходные данные – длина окружности.
Ограничения на результат – положительное число.
Ограничения на исходные данные – положительное число.

Математическая модель. Выразить радиус R из формулы длины окружности C= 2*π*R. Вычислить радиус R=C/(2* π). Вычислить площадь круга по формуле S= .

Описать переменные. Ввести данные.

Выразить радиус R из формулы длины окружности.

Вычислить радиус по формуле R=C/(2* π). Вычислить площадь круга по формуле S= .

Write( ‘Введите длину окружности С= ‘ );

WriteLn( ‘Площадь круга = ‘ , S: 5 : 3 );

Скриншот программы с результатами решения

Вывод. Программа работоспособна. Проверка результата с помощью калькулятора, получим число 426, 5116724. Значит, программа правильна.

Задача 3. Найти площадь кольца, внутренний радиус которого равен r, а внешний – заданному числу R (R> r).

Результат – найти площадь кольца.
Исходные данные – внутренний радиус равен r, а внешний – R (R> r).
Ограничения на результат – положительное число.
Ограничения на исходные данные – положительные числа.

Математическая модель. Найдём площадь кольца по формуле S к =π*(R*R-r*r), где – R — внешний радиус, r-внутренний радиуc, (R> r).

Описать переменные. Ввести данные.

Вычислить по формуле площадь кольца по формуле S к =π*(R*R-r*r).

Writeln( ‘Введите радиусы окружностей R2 и R1 ‘ );

S := pi * (R2 * R2 — R1 * R1);

WriteLn( ‘Площадь кольца S = ‘ , S: 5 : 3 );

Скриншот программы с результатами решения

Вывод. Программа работоспособна. Проверим результат с помощью калькулятора, получим число 12, 56637061. Верно.

Задача 4. Вычислить расстояние между двумя точками с координатами X1, Y1 и X2, Y2.

Результат – найти расстояние R между двумя точками на плоскости.
Исходные данные – даны координаты точек (X1, Y1) и (X2, Y2).
Ограничения на результат – ограничение на расстояние R>=0
Ограничения на исходные данные — ограничений на координаты нет.

Математическая модель. Выведем формулу для вычисления расстояния между двумя точками на плоскости.

Из точек A и B опустим перпендикуляры на оси координат.

Рассмотрим прямоугольный треугольник ∆ABC. Катеты этого треугольника равны:

AC = x b — x a ;
BC = y b — y a .

Воспользовавшись теоремой Пифагора, вычислим длину отрезка AB:

Подставив в это выражение длины отрезков AC и BC, выраженные через координаты точек A и B, получим формулу для вычисления расстояния между точками на плоскости: AB = .

Описать переменные. Ввести данные.

Вычислить расстояние между точками по формуле R= .

Напишем алгоритм на псевдокоде

* вывод (‘Введите координаты (x и y) точки 1’)

* вывод (‘Введите координаты (x и y) точки 2’)

* R := Sqrt(Sqr(X2 — X1) + Sqr(Y2 — Y1));

* вывод (‘расстояние между точками 1 и 2 равно ‘, R:10:3);

X1, X2, Y1, Y2, R: Real ;

Writeln( ‘Введите координаты (x и y) точки 1’ );

Writeln( ‘Введите координаты (x и y) точки 2’ );

R := Sqrt(Sqr(X2 — X1) + Sqr(Y2 — Y1));

Write( ‘расстояние между точками 1 и 2 равно ‘ , R: 10 : 3 );

Скриншот программы с результатами решения

Вывод. Программа работоспособна. Проверим результат с помощью калькулятора, получим число 4. Верно.

Задача 5. Найти площадь сектора, радиус которого равен 15.4, а дуга содержит заданное число радиан ϕ .

Результат – площадь сектора.
Исходные данные – величина угла в радианах.
Ограничения на результат – положительное число.
Ограничения на исходные данные – значение дуги в радианах меньше, чем 2π ≈ 6.28. Иначе сектор будет по величине больше круга.

Модель. Выведем формулу для вычисления площади сектора через угол, выраженный в радианах. Сектор круга ограничивается дугой между двумя точками А и В на окружности и двумя радиусами, проведёнными из концов дуги (точек А и В) к центру круга.

Два радиуса делят всю площадь круга на 2 сектора. Если угол между этими радиусами будет развёрнутым (180 0 ), то эти секторы будут между собой равны. Площадь сектора круга – это часть площади всей плоской фигуры, ограниченной окружностью с радиусом r. Площадь круга равна произведению квадрата радиуса на число S= . Площадь кругового сектора в радиан (полукруга) равна . Поэтому площадь сектора в один радиан в π раз меньше, т.е. равна : π. Значит, площадь сектора в α радиан равна =

* вывод (‘Введите величину дуги кругового сектора (в радианах)’)

* вывод (‘Площадь кругового сектора =’, S:8:2)

write(‘Введите величину дуги кругового сектора (в радианах) ‘);

writeln(‘Площадь кругового сектора = ‘, S:8:2)

Скриншот программы с результатами решения

Вывод. Программа работоспособна. Проверим результат с помощью калькулятора.

Задача 6. Даны координаты N точек на плоскости (x1,y1), (x2,y2), (x3,y3), . (xn,yn). Определить минимальный радиус круга, в который попадают все эти точки. Центр круга находится в начале координат.

Результат – определить минимальный радиус круга, в который попадают точки с заданными координатами.
Исходные данные – координаты N точек на плоскости (x1,y1), (x2,y2), (x3,y3), . (xn, yn).
Ограничения на результат – неотрицательное действительное число.
Ограничения на исходные данные – координаты точек выражаются действительными числами, количество точек N — натуральное число.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ И МЕТОД: Радиус круга с центром в начале координат вычисляется по формуле R= . Для наглядности рисунок.

АЛГОРИТМ. Вычисляем радиус (расстояние от начала координат до точки) для каждой точки, выбираем минимальное значение. Сравниваем два числа, наименьшее значение записываем как минимум. Это и будет минимальным значением радиуса. Так как количество точек известно, организуем цикл с параметром.