Радиус описанной окружности r 6 5 найдите sabc

Репетитор
по алгебре

Видео:найти радиус окружности, описанной вокруг треугольникаСкачать

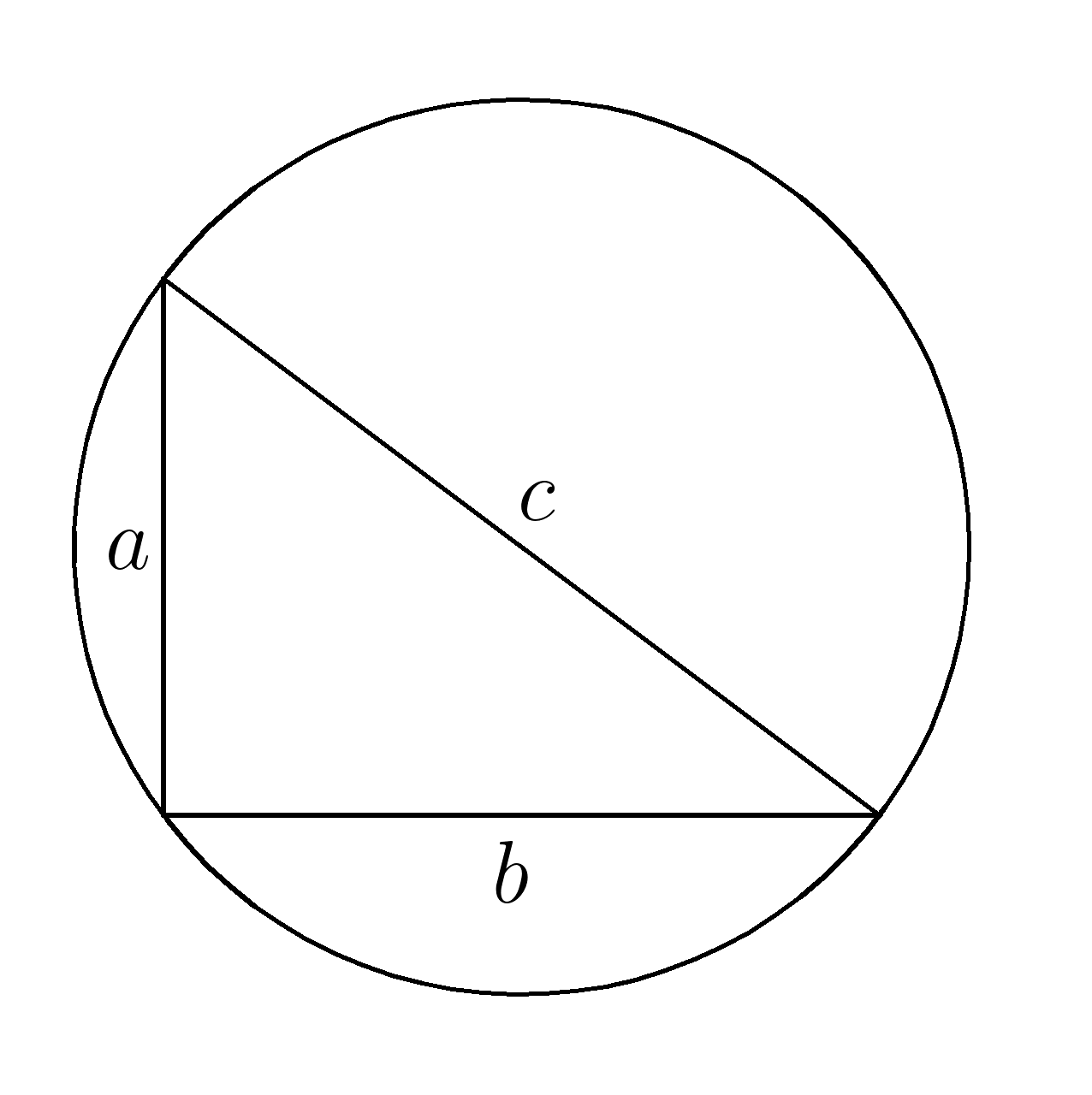
Описанная окружность

Около любого треугольника можно описать окружность

Центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров к сторонам треугольника.

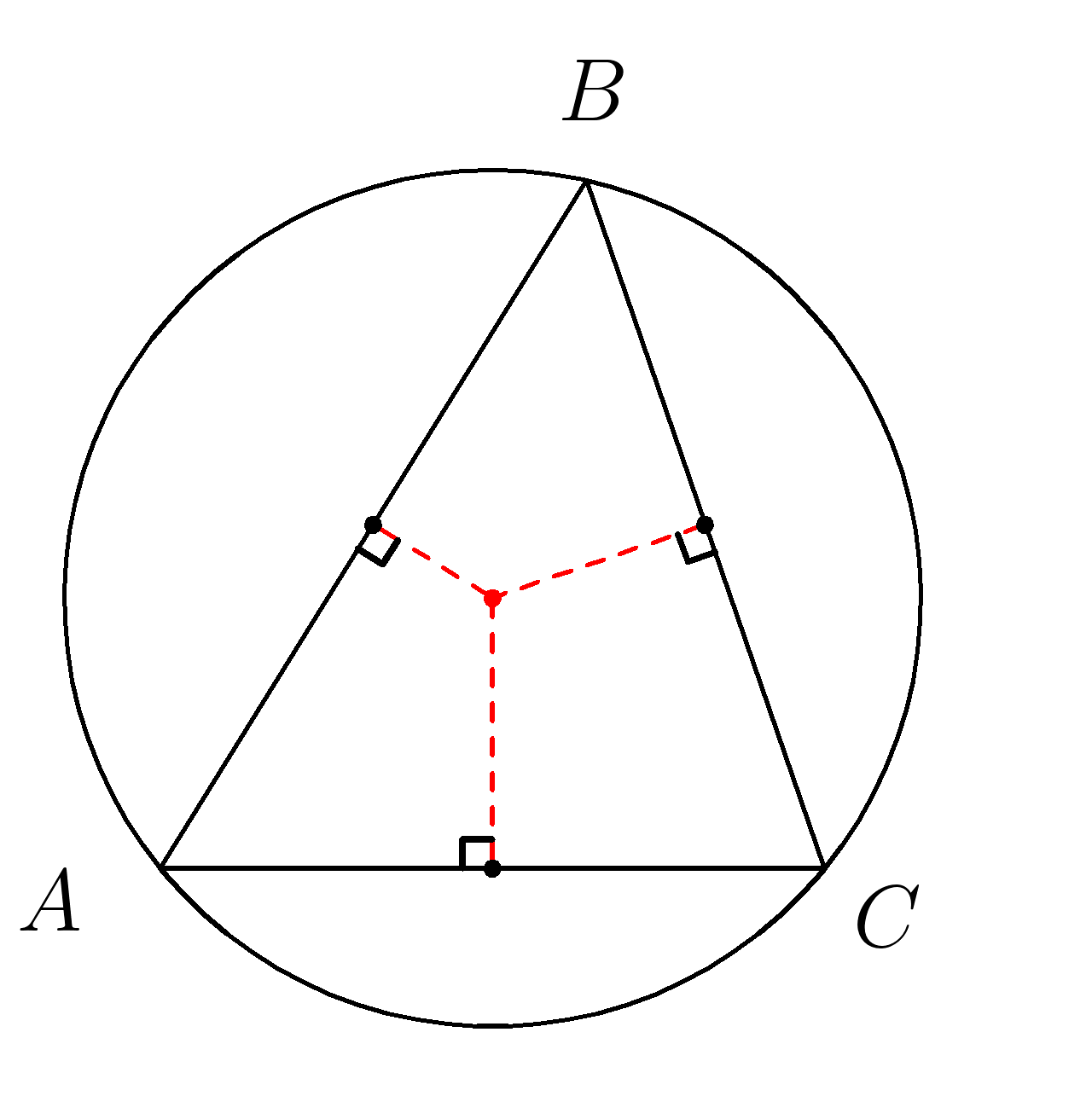
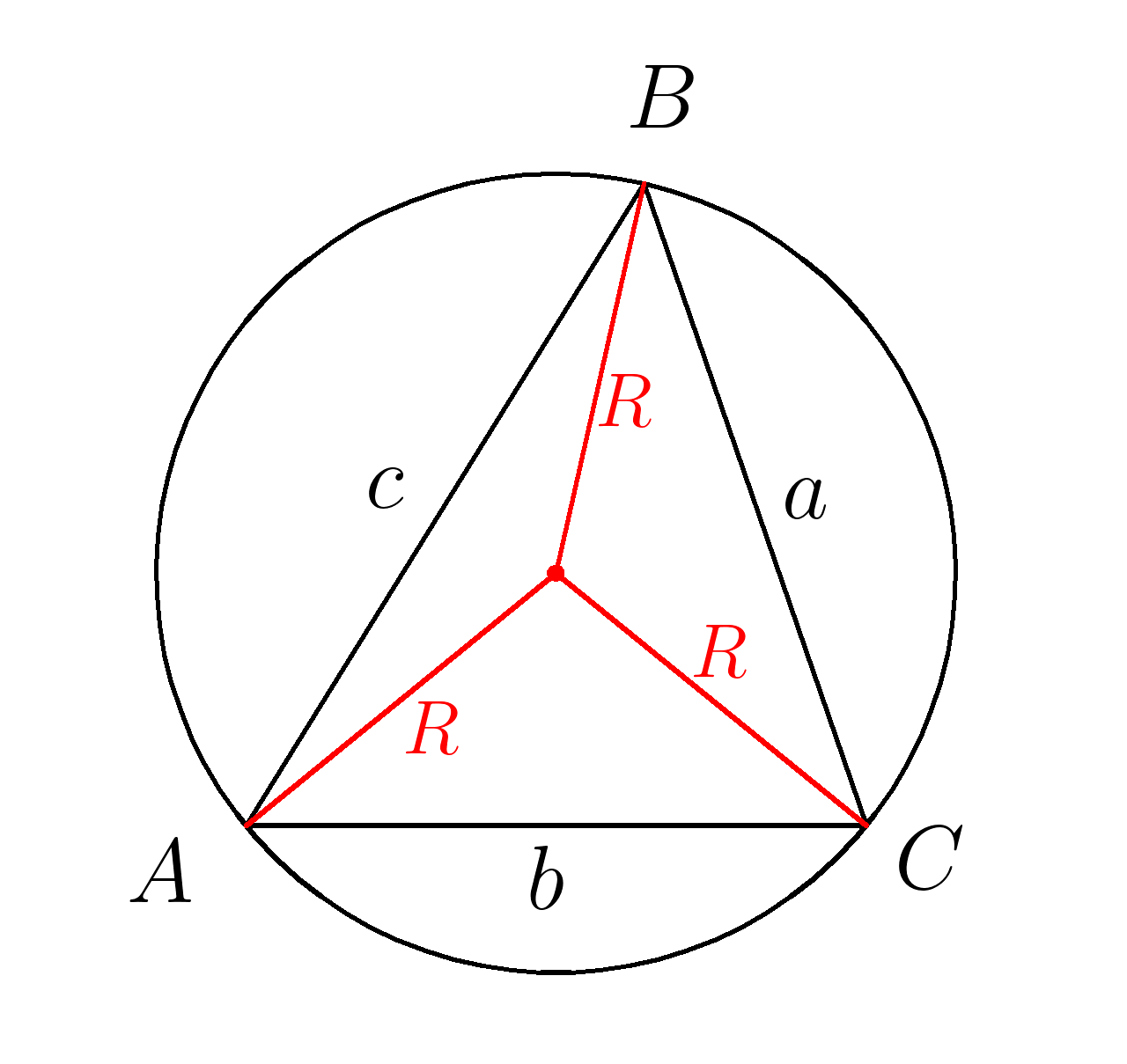
(R= dfrac )

(R) -радиус описанной окружности
(S) -площадь треугольника
(a) — сторона (BC)
(b) — сторона (AC)
(c) — сторона (AB)

1. Найти радиус описанной окружности, если площадь треугольника (S=6 ; ), а стороны (; a=3, ; b=4, ; c=5 )
Показать ответ Показать решение Видеорешение

Видео:Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

Треугольник описанный около окружности

Видео:№706. Найдите сторону равностороннего треугольника, если радиус описанной около него окружностиСкачать

Определение

Треугольник, описанный около окружности — это треугольник,
который находится около окружности и соприкасается
с ней всеми тремя сторонами.

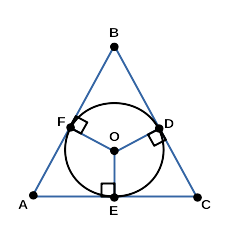
На рисунке ниже изображена окружность, вписанная в треугольник;
и треугольник, описанный около окружности.

△ ABC — треугольник, описанный около окружности;
A, B, C — вершины треугольника, описанного около окружности;
F, D, E — точки касания треугольника, описанного около окружности;
O — центр окружности, вписанной в треугольник;
OD = OF = OE — радиусы треугольника, описанного около окружности;
AB, BC, CA — касательные;
FA = AE, EC = CD, FB = BD — отрезки касательных;
OF ⟂ AB, OD ⟂ BC, OE ⟂ AC;

Треугольник ABC имеет три точки, где соприкасаются
стороны и сама окружность, эти точки называют точками
касания. У данного треугольника их всего три.

В любой треугольник можно вписать окружность, причем
только одну. Треугольник, в который вписана окружность
называется треугольником описанным около окружности.

Треугольники, описанные около окружности, обладают рядом
рядом отличительных свойств, характерных признаков, уникальными
терминами, а также формулам, по которым можно найти разные величины.

Формулы радиуса вписанной окружности, радиуса описанной окружности,
диаметра, средней линии, периметра, площади стороны позволяют выразить
одни величины через другие, рассчитать длину величины, узнать во сколько
раз одна величина отличается от другой, какая прослеживается взаимосвязь.

Длина любой величины произвольного
треугольника может измеряется в мм, см, м, км.

Видео:Задача 6 №27923 ЕГЭ по математике. Урок 140Скачать

Формулы

Радиус вписанной окружности в треугольник

r — радиус вписанной окружности треугольника, описанного около окружности.

1. Радиус вписанной окружности в треугольник,
   если известна площадь и все стороны:

Радиус вписанной окружности в треугольник,
если известны площадь и периметр:

Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:

Радиус описанной окружности около треугольника

R — радиус описанной окружности треугольника, описанного около окружности.

1. Радиус описанной окружности около треугольника,
   если известна одна из сторон и синус противолежащего стороне угла:

Радиус описанной окружности около треугольника,
если известны все стороны и площадь:

Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:

Площадь треугольника

S — площадь треугольника, описанного около окружности.

1. Площадь треугольника вписанного в окружность,
   если известен полупериметр и радиус вписанной окружности:

Площадь треугольника вписанного в окружность,
если известен полупериметр:

Площадь треугольника вписанного в окружность,
если известен высота и основание:

Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:

Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:

[ S = fracab cdot sin angle C ]

Периметр треугольника

P — периметр треугольника, описанного около окружности.

1. Периметр треугольника вписанного в окружность,
   если известны все стороны:
   

Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:

Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:

Сторона треугольника

a — сторона треугольника, описанного около окружности.

1. Сторона треугольника вписанного в окружность,
   если известны две стороны и косинус угла между ними:

Сторона треугольника вписанного в
окружность, если известна сторона и два угла:

Средняя линия треугольника

l — средняя линия треугольника, описанного около окружности.

1. Средняя линия треугольника вписанного
   в окружность, если известно основание:
   

Средняя линия треугольника вписанного в окружность,
если известны две стороны, ни одна из них не является
основанием, и косинус угла между ними:

Высота треугольника

h — высота треугольника, описанного около окружности.

1. Высота треугольника вписанного в окружность,
   если известна площадь и основание:

Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:

[ h = b cdot sin alpha ]

Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:

Видео:Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Свойства

Свойства треугольника, описанного около окружности,
а также окружности, вписанной в треугольник, медиан,
высот, биссектрис, радиусов-перпендикуляров.

Свойство 1. Окружность, можно вписать
в любой треугольник, только один раз.

Свойство 2. Центр окружности, вписанной в треугольник —
точка пересечения биссектрис, центр окружности.

Свойство 3. Центр окружности, описанной около треугольника —
точка пересечения серединных перпендикуляров.

Свойство 4. Центры вписанной и описанной окружностей
равностороннего треугольника, описанного около
окружности совпадают, имеют одну общую точку.

Свойство 5. Отрезок, проведенный из центра треугольника,
описанного около окружности, к любой из сторон,
является радиусом.

Свойство 6. У любого треугольника центр
вписанной окружности находится только внутри.

Свойство 7. Окружность находящаяся внутри
треугольника, описанного около окружности,
касается всех его сторон.

Свойство 8. Вписанная окружность и треугольник,
описанный около окружности, имеют три общие точки,
которые лежат на трех сторонах треугольника.

Свойство 9. Формула радиуса вписанной окружности
у треугольника, описанного около окружности, и четырехугольника,
у которого суммы противоположных равны, совпадает.

Свойство 10. Радиус описанной около треугольника окружности,
можно выразить и рассчитать через Теорему Синусов.

Свойство 11. У треугольника, описанного около
окружности, радиус вписанной окружности, можно
рассчитать через площадь и полупериметр.

Свойство 12. Радиус в точку касания есть перпендикуляр.

Свойство 13. Окружность, вписанная в треугольник, разделяет
стороны треугольника на 3 пары равных отрезков.

Свойство 14. Стороны треугольника, описанного около
окружности, можно также называть касательными.

Свойство 15. Отрезки, которые проведены из центра вписанной
окружности, к точкам касания, перпендикулярны сторонам.

Свойство 16. Сумма углов треугольника, описанного
около окружности, равна 180 градусам.

Свойство 17. Центр вписанной окружности
равноудален от всех сторон треугольника.

Свойство 18. Центр вписанной в треугольник окружности в научных
кругах называется замечательной точкой треугольника, либо инцентром.

Свойство 19. Правильный треугольник, описанный около
окружности, имеет точки касания с окружность, в серединах сторон.

Свойство 20. Равнобедренный, прямоугольный, равносторонний
треугольники, описанные около окружности, в точке пересечения
биссектрис и центре окружности, имеют одну общую точку.

Видео:Радиус описанной окружностиСкачать

Признаки существования

Признак 1. Центр вписанной окружности —
это точка пересечения биссектрис.

Признак 2. На сторонах треугольника лежат
три точки касания вписанной окружности.

Признак 3. Вписанная окружность делит смежные
стороны треугольника на равные отрезки касательных.

Признак 4. У вписанной окружности три радиуса в точку касания быть перпендикулярами.

Исходя из вышеперечисленных признаков, исходных
данных, внешнего вида, можно определить является ли
треугольник описанным около окружности или же нет.

Видео:Задача 6 №27926 ЕГЭ по математике. Урок 141Скачать

Признаки равенства

Признак 1. По двум сторонам и углу между ними.

Если две стороны и угол между ними одного треугольника, описанного
около окружности, равны двум сторонам и углу между ними другого
треугольника, описанного около окружности, то такие треугольники равны.

Признак 2. По стороне и двум прилежащим к ней углам.

Если сторона и два прилежащих к ней угла одного треугольника, описанного
около окружности, равны стороне и двум прилежащим к ней углам другого
треугольника, описанного около окружности, то такие треугольники равны.

Признак 3. По трем сторонам.

Если три стороны одного треугольника, описанного
около окружности, равны трем сторонам другого
треугольника, описанного около окружности.

Как мы знаем, любой треугольник может быть описан около
окружности, исходя из этого можно сказать, что около
окружности, могут быть описаны следующие виды треугольников:

1. Разносторонний треугольник
2. Равносторонний / правильный треугольник
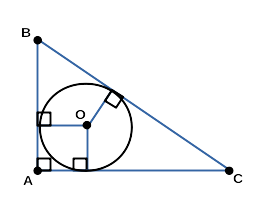
3. Прямоугольный треугольник
4. Равнобедренный треугольник
5. Равнобедренныйпрямоугольный треугольник

• Прямоугольный треугольник, описанный около окружности

Характерные признаки: один из углов прямой,
длину сторон можно найти через Теорему
Пифагора, сумма острых углов 90 градусов.

Основные формулы:

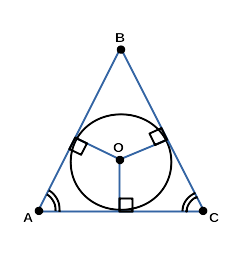
• Равнобедренный треугольник, описанный около окружности
  

Характерные признаки: два угла равны,
две стороны равны, третий угол можно
найти зная два других.

Основные формулы:

• Равносторонний треугольник, описанный около треугольника

Характерные признаки: три угла и три стороны равны, точки пересечения медиан, высот, биссектрис совпадают.

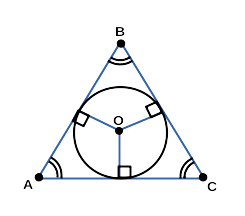
Основные формулы:

Видео:Геометрия Радиус окружности описанной около треугольника ABC равен 6 см Найдите радиус окружностиСкачать

Термины

Точка касания — это точка, где соприкасается вписанная
окружность с треугольником; это общая точка, для окружности
и треугольника, которая лежит на любой из сторон треугольника.

Инцентр — это точка, где пересекаются три биссектрисы
треугольника; это центр вписанной окружности в треугольник;
это одна из замечательных точек в геометрии.

Касательная — это сторона треугольника, которая имеет с
вписанной окружностью одну общую точку — точку касания.

Ортоцентр — точка, где пересекаются высоты треугольника.

Ось симметрии — это прямая, которая делит
треугольник на равные половины.

Замечательная точка — это точка пересечения медиан,
высот, биссектрис, серединных перпендикуляров.

Отрезок касательной — это отрезок, который берет начало
у одной из вершин треугольника, и имеет конец в точке касания.

Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Систематизация знаний по геометрии при подготовке к ЕГЭ по теме «Вписанные и описанные окружности. Треугольник. Четырехугольник»

Разделы: Математика

На итоговых уроках по геометрии времени на то, чтобы прорешать задачи по всему курсу в целом практически не остается. А в КИМы ЕГЭ традиционно включаются задачи, решение которых требует знаний планиметрии по теме «Вписанные и описанные окружности». Поэтому предложенный материал поможет не только вспомнить данную тему, но и систематизировать ранее полученные знания по решению планиметрических задач на вписанные и описанные окружности, а также подготовиться к решению подобных задач в ЕГЭ. При этом предполагается, что ученик хотя бы на минимальном уровне владеет всем курсом школьной геометрии (планиметрии).

Первым и важнейшим этапом решения геометрической задачи является построение чертежа. Нельзя научиться решать достаточно содержательные задачи, не выработав прочных навыков по изготовлению «хороших» чертежей, не выработав привычки (даже рефлекса) – не начинать решать задачу, пока не сделан «большой и красивый» чертеж. В качестве основного метода решения геометрических задач выдвигается алгебраический метод с составлением последующего алгоритма. Ставя во главу угла алгебраический метод, необходимо предостеречь от чрезмерного увлечения алгеброй и счетом, не забывать о том, что речь идет все же о геометрических задачах, а поэтому, работая над задачей, следует искать геометрические особенности, учиться смотреть и видеть геометрию. Выделив два слагаемых, определяющих умение решать геометрические задачи, – чертеж плюс метод, добавим сюда третье – владение определенными теоремами и опорными задачами, известными геометрическими фактами.

I. Необходимые теоремы и опорные задачи для окружности, вписанной в треугольник и четырехугольник, и окружности, описанной около треугольника и четырехугольника. (Приложение 1)

II. Решение задач по готовым чертежам (удобно воспользоваться кодоскопом).

При этом ученики устно объясняют ход решения задач, формулируют теоремы и опорные задачи, применяемые при решении задач по готовым чертежам.

Готовый чертеж

Дано
Найти

Решение
Ответ

AB = BC

P_ABC = ?Отрезки касательных равны: BM = BK = 5
AB = BC = 12
MC = CN = 7, AC = 14, AK = AN = 7,
PABC = 12 + 12 + 14 = 38
Ответ: P_ABC = 38

AB = 6,
АО =

P_ABC = ?Отрезки касательных равны: АВ = ВС
1) ,
2) АВ = ВС, , т.к. ВО – биссектриса
3) АВС – равносторонний, PABC = 6 • 3 = 18
Ответ: P_ABC = 18

AD – диаметр окружности,
АВ = 3,
ВД = 4
1. Доказать: NM AD
2. R = ?1. Т.к. AD – диаметр, то DB AN и AC DN, т.е. AC и DB – высоты АND, тогда NK – высота, т.к. они пересекаются в одной точке.
Значит NM AD.
2. AD = = 5, R =
Ответ: R = 2,5

R = ?AC – диаметр окружности и гипотенуза прямоугольного АВС, R = = 1,5
Ответ: R = 1,5

AB = 24,
ОК = 5

R = ?О – точка пересечения серединных перпендикуляров к сторонам .
BKO – прямоугольный, ВК = AK = 12,
КО = 5, ВО = = 13 = R
Ответ: R = 13

III. Решение задач.

1. Найти периметр прямоугольного треугольника, если радиус вписанной окружности 2 см, а гипотенуза 13 см.

Пусть AM = AN = x, тогда AC = x + 2, CB = 2 + 13 – x = 15 – x (x + 2) 2 + (15 – x) 2 = 169 x 2 – 13x + 30 = 0 x1 = 10, x2 = 3; AC = 6, CB = 12; P = 30 см Ответ: P = 30 см.

2. Радиус вписанной в прямоугольный треугольник окружности 3 см, О – центр вписанной окружности, , . Найти площадь треугольника.

АО – биссектриса, AKO – прямоугольный, sin = sin 30 о = , АО = 6, AN = AK = = 3, AC = 3 + 3, tg 60 о = , CB = SABC = = Ответ: S = см2.

3. Периметр треугольника 84. Точка касания вписанной окружности делит одну из сторон на отрезки 12 и 14. Найти радиус вписанной окружности и площадь АВС, если ОВ = 18, О – центр вписанной окружности.

P = 84, KB = BN = 16, ON = = = r AB = 28, BC = 30, AC = 26 По формуле Герона: SABC = = 336 Ответ: r = ; S = 336.

4. В равнобедренном треугольнике расстояние от центра вписанной окружности до вершины не равного угла 5 см. Большая сторона 10 см. Найти радиус вписанной окружности.

OB = 5, , OM = OB . = , BH = 5 + r, AH = 2r, AHB – прямоугольный, 4r 2 = 100 – (5 + r) 2 , r 2 + 2r – 15 = 0, r1 = – 5, r2 = 3 Ответ: r = 3 см.

5. Основание равнобедренного треугольника, вписанного в окружность радиуса 5 см, равно 6 см. Найти периметр треугольника.

AHO – прямоугольный: OH = 4, BH = 4 + 5 =9, AB = BC = = P = Ответ: P = см.

6. Периметр треугольника АВС равен 72 см. AB = BC, AB:AC = 13:10. Найти радиус описанной около треугольника окружности.

AB + BC + AC = 72, , AC = 20, AB = BC = = 26, BH = = 24 BN = NA = 13, , R = Ответ: R = см.

7. Основание тупоугольного равнобедренного треугольника равно 24 см, а радиус описанной окружности 13 см. Найти боковую сторону треугольника.

OC = 13, AC = 24, HC = 12 HOC – прямоугольный, OH = = 5 BH = BO – OH =13 – 5 = 8 BHC – прямоугольный, BC = Ответ: см.

8. Окружность, диаметром которой служит АС треугольника АВС, проходит через точку пересечения медиан этого треугольника. Найти отношение длины стороны АС к длине проведенной к ней медианы.

AO = OC = R = OM, BM = 2R, BO = 3R, Ответ: .

9. Найдите площадь равнобедренной трапеции, описанной около окружности с радиусом 4, если известно, что боковая сторона трапеции равна 10.

SABCD = Т.к. окружность вписанная, то AB + CD = AD + BC = 20 h = 2r = 8, , SABCD = 10 • 8 = 80 Ответ: 80.

10. Дан ромб ABCD. Окружность, описанная около треугольника ABD, пересекает большую диагональ ромба AC в точке E. Найдите CE, если AB = , BD = 16.

AOB – прямоугольный: AO = = 16 AD = 32 По теореме об отрезках пересекающихся хорд: BO • OD = AO • OE, 8 • 8 = 16 • OE, OE = 4, CE = 16 – 4 = 12 Ответ: 12.

IV. Задачи для самостоятельного решения.

1. Радиус окружности, вписанной в прямоугольный треугольник, равен 2 см, а радиус описанной окружности равен 5 см. Найдите больший катет треугольника.

2. Около равнобедренного треугольника с основанием АС и углом при основании 75о описана окружность с центром О. Найдите ее радиус, если площадь треугольника ВОС равна 16.

3. Найдите радиус окружности, вписанной в остроугольный треугольник АВС, если высота BH равна 12 и известно, что , .

4. Один из катетов прямоугольного треугольника равен 15, а проекция второго катета на гипотенузу равна 16. Найдите диаметр окружности, описанной около этого треугольника.

5. В равнобедренный треугольник АВС вписана окружность. Параллельно его основанию АС проведена касательная к окружности, пересекающая боковые стороны в точках D и E. Найдите радиус окружности, если DE = 8, AC = 18.

6. Около треугольника ABC описана окружность. Медиана треугольника AM продлена до пересечения с окружностью в точке K. Найдите сторону AC, если AM= 18, MK = 8, BK = 10.

7. Окружность, вписанная в равнобедренный треугольник, касается его боковых сторон в точках K и A. Точка K делит сторону этого треугольника на отрезки 15 и 10, считая от основания. Найдите длину отрезка KA.

8. Угол В треугольника АВС равен 60 о , радиус окружности, описанной около АВС, равен 2. Найти радиус окружности, проходящей через точки А и С и центр окружности, вписанной в АВС.

9. Стороны треугольника равны 5, 6 и 7. Найти отношение отрезков, на которые биссектриса большего угла этого треугольника разделена центром окружности, вписанной в треугольник.

10. Радиус окружности, вписанной в прямоугольный треугольник, равен полуразности его катетов. Найти отношение большего катета к меньшему.

Ответ: ().

11. Диагонали четырехугольника ABCD, вписанного в окружность, пересекаются в точке М, прямые AB и CD пересекаются в точке N. Известно, что , . Найти и .

12. Высоты AH и BK остроугольного треугольника ABC пересекаются в точке M, . Найдите градусную меру угла ABO, где O – центр окружности, описанной около треугольника ABC.

13. Около окружности описана равнобочная трапеция с основаниями 5 и 3. Найти радиус окружности.

Ответ: ().

14. В равнобедренный АВС с основанием BC вписана окружность. Она касается стороны AB в точке M. Найдите радиус окружности, если AM = 6, BM = 24.

15. Дан прямоугольный треугольник ABC с прямым углом C. Через центр O вписанной в треугольник окружности проведен луч BO, пересекающий катет AC в точке M. Известно, что AM = , . Найдите гипотенузу и радиус окружности, описанной около треугольника.

🔥 Видео

Окружность вписанная в треугольник и описанная около треугольника.Скачать

Задача 6 №27932 ЕГЭ по математике. Урок 146Скачать

Задача 6 №27913 ЕГЭ по математике. Урок 131Скачать

Задача 6 №27909 ЕГЭ по математике. Урок 129Скачать

Задача 6 №27900 ЕГЭ по математике. Урок 128Скачать

Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать

Задача 6 №27910 ЕГЭ по математике. Урок 130Скачать

ЕГЭ Математика Задание 6#27935Скачать

ЕГЭ профиль #3 / Радиус описанной окружности / Равносторонний треугольник / решу егэСкачать

2047 радиус окружности описанной около правильного треугольника равна 36 корней из 3Скачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать