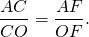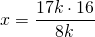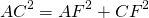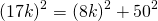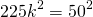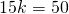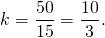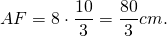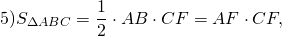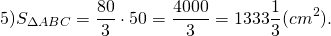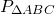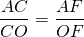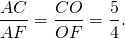Решение задач на вписанную окружность в равнобедренный треугольник

Знание — сила. Познавательная информация

Видео:Геометрия К окружности, вписанной в равнобедренный треугольник с основанием 12 см и высотой 8 смСкачать

Окружность, вписанная в равнобедренный треугольник

Если в задача дана окружность, вписанная в равнобедренный треугольник, в ее решении могут быть использованы свойства касательных и свойство биссектрисы треугольника.

Центр вписанной в треугольник окружности является точкой пересечения его биссектрис. Поскольку в равнобедренном треугольнике биссектриса, проведенная к основанию, совпадает с медианой и высотой, то центр вписанной в равнобедренный треугольник окружности лежит на высоте и медиане, проведенных к основанию .

Рассмотрим две задачи на вписанную в равнобедренный треугольник окружность.

Боковая сторона равнобедренного треугольника делится точкой касания вписанной окружности в отношении 8:9, считая от вершины угла при основании треугольника. Найти площадь треугольника, если радиус вписанной окружности равен 16 см.

окружность (O, r) — вписанная,

F, K, M, — точки касания со сторонами AB, BC, AC,

1) Пусть k — коэффициент пропорциональности (k>0). Тогда AM=8k см, MC=9k см.

2) По свойству касательных, проведенных из одной точки,

AF=AM=8k см, CK=MC=9k см.

Так как AC=BC, то BK=AM и BF=BK=8k см.

3) Центр вписанной окружности является точкой пересечения биссектрис треугольника.

Так как ∆ ABC — равнобедренный с основанием AB, то CF — высота, медиана и биссектриса ∆ ABC.

4) Рассмотрим треугольник AFC.

∠AFC=90, AF=8k см, AC=AM+MC=17k см.

OF=r. Пусть CO=x см, тогда

CO=34 см, CF=CO+OF=34+16=50 см.

По теореме Пифагора:

Ответ: 1333 1/3 кв.см.

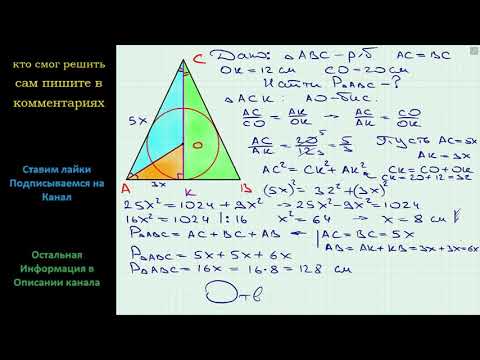
Центр окружности, вписанной в равнобедренный треугольник, делит высоту, проведенную к основанию, в отношении 5:4. Найти периметр треугольника, если боковая сторона меньше основания на 15 см.

Дано: ∆ ABC, AC=BC,

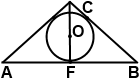
окружность (O, r) — вписанная,

CF — высота, CO:OF=5:4, AC

1) Рассмотрим ∆ ACF — прямоугольный (так как CF — высота треугольника по условию).

Центр вписанной в треугольник окружности есть точка пересечения его биссектрис.

По свойству биссектрисы треугольника,

Пусть k — коэффициент пропорциональности, тогда AC=5k см, AF=4k см, AB=2AF=8k см.

Следовательно, AC=BC=5∙5=25 см, AB=8∙5=40 см.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Решение задач на вписанную окружность в равнобедренный треугольник

Радиус окружности, вписанной в правильный треугольник, равен 6. Найдите высоту этого треугольника.

значит,

Приведем другое решение.

Высота правильного треугольника равна 3 радиусам вписанной окружности, поэтому она равна 18.

Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60°, большее основание равно 12. Найдите радиус описанной окружности этой трапеции.

Окружность, описанная вокруг трапеции, описана и вокруг треугольника Это треугольник равнобедренный, угол при вершине равен 120°, углы при основании равны 30°. Найдем его боковую сторону:

откуда Тогда по теореме синусов:

Приведем другое решение (Р. А., СПб.).

Хорды AD, DC и CB равны, поэтому равны и стягиваемые ими дуги. Вписанный угол А равен 60°, он опирается на две из этих дуг и равен половине их суммы. Поэтому каждая из дуг равна 60°, их сумма равна 180°, а хорда АВ является диаметром. Отсюда получаем, что искомый радиус равен 6.

Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Урок одной задачи (вписанная и описанная окружность в р/б треуг-к)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся

Сертификат и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Тема урока: «Вписанная и описанная окружность. Решение задач. (Урок одной задачи.)». Цель урока: обобщить и систематизировать знания по теме «вписанная и описанная окружность». Задачи урока: привитие навыков в отыскании различных способов решения задач, развитие исследовательских способностей у учащихся. Учитель ГОУ СОШ № 250: Самсонова М. Н. Санкт-Петербург

Тема урока: «Вписанная и описанная окружность. Решение задач. (Урок одной задачи.)». План урока: 1. Постановка цели и задач урока. 2. Повторение. Подготовка к решению задачи. 3. Решение одной задачи несколькими способами. 4. Подведение итогов урока. 5. Домашнее задание.

Определение подобных треугольников. Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника. С А В A1 C1 B1 AB и A1B1, BC и B1C1, AC и A1C1 – сходственные стороны

A B C A1 B1 C1 I. Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны. Признаки подобия треугольников.

A B C A1 B1 C1 II. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то такие треугольники подобны. Признаки подобия треугольников.

A B C A1 B1 C1 III. Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны. Признаки подобия треугольников.

A B C Биссектриса угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам. Свойство биссектрисы угла треугольника. D

Свойство пересекающихся хорд. Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. АЕ  ЕВ = СЕ  ЕD

А M B C Свойство касательной и секущей, проведённых их одной точки. Если из точки М к окружности проведены касательная и секущая, то квадрат отрезка касательной от точки М до точки касания равен произведению длин отрезков секущей от точки М до точек её пересечения с окружностью.

А О B C Теорема о вписанном угле. Вписанный угол измеряется половиной дуги, на которую он опирается.

Формулы для нахождения площади треугольника.

Задача: Найдите радиус r вписанной и радиус R описанной окружности для равнобедренного треугольника с основанием 10 см и боковой стороной 13 см. Способ 1. Из находим по теореме Пифагора см, точка О – центр описанной окружности, и . Из по теореме Пифагора , а , следовательно, см, откуда см.

Задача: Найдите радиус r вписанной и радиус R описанной окружности для равнобедренного треугольника с основанием 10 см и боковой стороной 13 см. Способ 1. О1 – центр вписанной окружности, . Так как , то и см, а . Из по теореме Пифагора , т. е. , откуда см.

Задача: Найдите радиус r вписанной и радиус R описанной окружности для равнобедренного треугольника с основанием 10 см и боковой стороной 13 см. α Способ 2. Пусть имеем тогда из следует, что т. е. и Пусть , тогда . Из см.

Задача: Найдите радиус r вписанной и радиус R описанной окружности для равнобедренного треугольника с основанием 10 см и боковой стороной 13 см. Способ 3. Из подобия треугольников ОВК и CBD имеем , т. е. и см. Так как

Задача: Найдите радиус r вписанной и радиус R описанной окружности для равнобедренного треугольника с основанием 10 см и боковой стороной 13 см. Способ 4. Используя свойство двух пересекающихся хорд АС и ВЕ окружности, получаем: , т. е. , отсюда см. Используя свойство биссектрисы СО1 треугольника BDC, имеем , ,откуда см.

Задача: Найдите радиус r вписанной и радиус R описанной окружности для равнобедренного треугольника с основанием 10 см и боковой стороной 13 см. Способ 5. Продолжив BD до пересечения с описанной окружностью, получим прямоугольный треугольник ВСЕ, откуда и см.

Задача: Найдите радиус r вписанной и радиус R описанной окружности для равнобедренного треугольника с основанием 10 см и боковой стороной 13 см. Способ 5. Для нахождения r этим способом учащихся предварительно надо познакомить с зависимостью между касательной и секущей, проведёнными из одной точки к окружности. Используя эту зависимость, имеем , т. е. , откуда см.

Задача: Найдите радиус r вписанной и радиус R описанной окружности для равнобедренного треугольника с основанием 10 см и боковой стороной 13 см. Способ 6. Если , то , как внешний угол равнобедренного (другое обоснование: так как точка В лежит по одну сторону с центром О относительно прямой ЕС, то по свойству вписанного угла ). Из см

Задача: Найдите радиус r вписанной и радиус R описанной окружности для равнобедренного треугольника с основанием 10 см и боковой стороной 13 см. Способ 6. Из имеем . Так как , то и см.

Задача: Найдите радиус r вписанной и радиус R описанной окружности для равнобедренного треугольника с основанием 10 см и боковой стороной 13 см. Способ 7. Вычислив см и см², найдём R и r по формулам и , где a, b, c – стороны треугольника, S – его площадь.

При решении задач только одним способом единственная цель – найти правильный ответ. Если же требуется применить при этом несколько способов, стараешься отыскать наиболее оригинальное, красивое, экономичное решение. Для этого приходится вспоминать многие теоретические факты, методы и приёмы, анализировать их с точки зрения применимости к данной в задаче ситуации, накапливается определённый опыт применения одних и тех же знаний к различным вопросам. Всё это активизирует учебную деятельность, прививает интерес к предмету. Подведение итогов урока.

Домашнее задание: № 689 (рассмотреть задачу тремя наиболее понравившимися способами).

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 989 человек из 79 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 681 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 313 человек из 70 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Геометрия Центр окружности, вписанной в равнобедренный треугольник, делит его высоту, проведеннуюСкачать

Дистанционные курсы для педагогов

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 523 489 материалов в базе

Материал подходит для УМК

«Геометрия. 7-9 класс», Волович М.Б., Атанасян Л.С.

Глава 4. Окружность

Другие материалы

• 26.01.2018
• 4597
• 15

• 25.01.2018
• 323
• 0

• 25.01.2018
• 2018
• 76

• 24.01.2018
• 1800
• 18

• 24.01.2018
• 1749
• 8

• 24.01.2018
• 3527
• 6

• 22.01.2018
• 813
• 0

• 22.01.2018
• 459
• 5

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 26.01.2018 2710
• PPTX 1.5 мбайт
• 9 скачиваний
• Рейтинг: 5 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Самсонова Мария Николаевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 5 лет и 3 месяца
• Подписчики: 0
• Всего просмотров: 2766
• Всего материалов: 1

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:№691. Точка касания окружности, вписанной в равнобедренный треугольник, делит однуСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Ставропольских школьников с 1 по 8 класс перевели на дистанционное обучение

Время чтения: 2 минуты

В Рособрнадзоре видят предпосылки к снижению качества знаний у школьников на фоне пандемии

Время чтения: 1 минута

Онлайн-тренинг о способах взаимодействия с разными категориями учащихся

Время чтения: 2 минуты

Петербургских школьников с 7 по 11 классы перевели на дистанционное обучение

Время чтения: 1 минута

В Петербурге введут новые COVID-ограничения для несовершеннолетних

Время чтения: 2 минуты

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

📹 Видео

Геометрия Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковыхСкачать

Вписанная и описанная около равнобедренного треугольника, окружностьСкачать

Геометрия Найдите отношение радиуса окружности, вписанной в равнобедренный прямоугольный треугольникСкачать

Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Геометрия Радиус окружности вписанной в равнобедренный треугольник, составляет 2/9 высотыСкачать

Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

ЕГЭ ВАУ ХАУ ВПИСАННАЯ ОКРУЖНОСТЬ В РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК ПОЩЕЧИНА | ГАРМАШУК 007Скачать

Строим вписанную в данный треугольник окружность (Задача 2).Скачать

Геометрия 8 класс : Решение задач. Вписанная окружностьСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Геометрия В равнобедренный треугольник вписана окружность Точка касания делит боковую сторонуСкачать

Планиметрия 28 | mathus.ru | Радиус окружности, вписанной в равнобедренный треугольникСкачать

Свойство окружности, описанной около равнобедренного треугольникаСкачать

Геометрия Радиус окружности, вписанной в равнобедренный треугольник, равен 12 см, а расстояние отСкачать