Число векторов фундаментальной системы решений

Видео:ФСР. Система однородных уравнений. Общее решениеСкачать

Однородные СЛАУ

Однородной СЛАУ называется система, все правые части которой равны нулю одновременно.

Однородная СЛАУ, записанная в матричном виде, $A X=Theta$ всегда совместна, так как $X=Theta$ всегда является ее решением.

Заметим, что если $x_, x_$ — это два решения однородной СЛАУ, то их линейная комбинация также будет решением однородной СЛАУ:

$$Y=lambda_ x_+lambda_ x_$$ $$A Y=Aleft(lambda_ x_+lambda_ x_right)=lambda_ A x_+lambda_ A x_=lambda_ Theta+lambda_ Theta=Theta$$

Если однородная квадратная СЛАУ имеет ненулевое решение, то определитель матрицы системы равен нулю.

Задание. Выяснить, имеет ли однородная СЛАУ $left<begin 3 x-2 y=-1 \ x+3 y=7 endright.$ ненулевые решения.

$$Delta=left|begin 3 & -2 \ 1 & 3 endright|=9-(-2)=9+2=11 neq 0$$

Так как определитель не равен нулю, то система имеет только нулевое решение $x=y=0$

Ответ. Система имеет только нулевое решение.

Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Фундаментальная система решений

Рассмотрим множество всех столбцов, которые являются решениями исходной системы.

Фундаментальной системой решений (ФСР) однородной СЛАУ называется базис этой системы столбцов.

Количество элементов в ФСР равно количеству неизвестных системы минус ранг матрицы системы. Любое решение исходной системы есть линейная комбинация решений ФСР.

Общее решение неоднородной СЛАУ равно сумме частного решения неоднородной СЛАУ и общего решения соответствующей однородной СЛАУ.

Задание. Найти общее решение и ФСР однородной системы $left<begin x_+x_-3 x_-x_=0 \ x_-x_+2 x_-x_=0 \ 4 x_-2 x_+6 x_+3 x_-4 x_=0 \ 2 x_+4 x_-2 x_+4 x_-7 x_=0 endright.$

Решение. Приведем систему к ступенчатому виду с помощью метода Гаусса. Для этого записываем матрицу системы (в данном случае, так как система однородная, то ее правые части равны нулю, в этом случае столбец свободных коэффициентов можно не выписывать, так как при любых элементарных преобразованиях в правых частях будут получаться нули):

$$A=left(begin 1 & 1 & 0 & -3 & -1 \ 1 & -2 & 2 & -1 & 0 \ 4 & -2 & 6 & 3 & -4 \ 2 & 4 & -2 & 4 & -7 endright)$$

с помощью элементарных преобразований приводим данную матрицу к ступенчатому виду. От второй строки отнимаем первую, от третьей — четыре первых, от четвертой — две первых:

$$A simleft(begin 1 & 1 & 0 & -3 & -1 \ 0 & -2 & 2 & 2 & 1 \ 0 & -6 & 6 & 15 & 0 \ 0 & 2 & -2 & 10 & -5 endright)$$

Обнуляем элементы второго столбца, стоящие под главной диагональю, для этого от третьей строки отнимаем три вторых, к четвертой прибавляем вторую:

$$A simleft(begin 1 & 1 & 0 & -3 & -1 \ 0 & -2 & 2 & 2 & 1 \ 0 & 0 & 0 & 9 & -3 \ 0 & 0 & 0 & 12 & -4 endright)$$

От четвертой строки отнимем $frac$ третьей и третью строку умножим на $frac$ :

$$A simleft(begin 1 & 1 & 0 & -3 & -1 \ 0 & -2 & 2 & 2 & 1 \ 0 & 0 & 0 & 3 & -1 \ 0 & 0 & 0 & 0 & 0 endright)$$

Нулевые строки можно далее не рассматривать, тогда получаем, что

$$A simleft(begin 1 & 1 & 0 & -3 & -1 \ 0 & -2 & 2 & 2 & 1 \ 0 & 0 & 0 & 3 & -1 endright)$$

Далее делаем нули над главной диагональю, для этого от первой строки отнимаем третью, а ко второй строке прибавляем третью:

$$A simleft(begin 1 & 1 & 0 & -6 & 0 \ 0 & -2 & 2 & 5 & 0 \ 0 & 0 & 0 & 3 & -1 endright)$$

то есть получаем систему, соответствующую данной матрице:

Или, выразив одни переменные через другие, будем иметь:

Здесь $x_, x_$ — независимые (или свободные) переменные (это те переменные, через которые мы выражаем остальные переменные), $x_, x_, x_$ — зависимые (связанные) переменные (то есть те, которые выражаются через свободные). Количество свободных переменных равно разности общего количества переменных $n$ (в рассматриваемом примере $n=5$ , так как система зависит от пяти переменных) и ранга матрицы $r$ (в этом случае получили, что $r=3$ — количество ненулевых строк после приведения матрицы к ступенчатому виду): $n-r=5-3=2$

Так как ранг матрицы $r=3$ , а количество неизвестных системы $n=5$ , то тогда количество решений в ФСР $n-r=5-3=2$ (для проверки, это число должно равняться количеству свободных переменных).

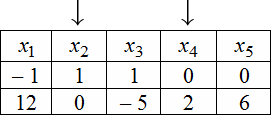
Для нахождения ФСР составляем таблицу, количество столбцов которой соответствует количеству неизвестных (то есть для рассматриваемого примера равно 5), а количество строк равно количеству решений ФСР (то есть имеем две строки). В заголовке таблицы выписываются переменные, свободные переменные отмечаются стрелкой. Далее свободным переменным придаются любые, одновременно не равные нулю значений и из зависимости между свободными и связанными переменными находятся значения остальных переменных. Для рассматриваемой задачи эта зависимость имеет вид:

Тогда придавая в первом случае, например, независимым переменным значения $x_=1$ , $x_=0$ получаем, что $left<begin x_=-1+6 cdot 0=-1 \ x_=1-frac cdot 0=1 \ x_=3 cdot 0=0 endright.$ . Полученные значения записываем в первую строку таблицы. Аналогично, беря $x_=0$ , $x_=2$, будем иметь, что <x_=12, x_=-5, x_=6> , что и определяет второе решение ФСР. В итоге получаем следующую таблицу:

Эти две строчки и есть фундаментальным решением заданной однородной СЛАУ. Частное решение системы:

$$X_=left(begin -1 \ 1 \ 1 \ 0 \ 0 endright), X_=left(begin 12 \ 0 \ -5 \ 2 \ 6 endright)$$

Общее решение является линейной комбинацией частных решений:

$$X=C_ X_+C_ X_=C_left(begin -1 \ 1 \ 1 \ 0 \ 0 endright)+C_left(begin 12 \ 0 \ -5 \ 2 \ 6 endright)$$

где коэффициенты $C_, C_$ не равны нулю одновременно. Или запишем общее решение в таком виде:

Придавая константам $C_, C_$ определенные значения и подставляя их в общее решение, можно будет находить частные решения однородной СЛАУ.

Видео:Фундаментальная система решений системы линейных уравнений ФСР СЛАУСкачать

Фундаментальная система решений СЛАУ

Вы будете перенаправлены на Автор24

Системой линейных уравнений называется система вида: $begin a_ cdot x_1 +. + a_ cdot x_n = b_1 \ . \ a_ cdot x_1 + a_ cdot x_n = b_m end$

Здесь каждая буква относится к своей группе обозначений, $x_1. x_n$ — это неизвестные числа или переменные, подлежащие поиску, $a_11. a_$ — множители, содержащиеся при неизвестных, $b_1. b_m$ — свободные члены таблицы из чисел, получаемой на основе приведённой СЛАУ.

В компактной форме СЛАУ принято записывать в виде формулы вида $A cdot X = B$. В этой формуле под большой буквой $A$ подразумевается матрица множителей при неизвестных системы, а буквами $X$ и $B$ обозначены вектор-столбец неизвестных системы и свободных членов.

Матрица $A$ называется основной матрицей системы, вот как она будет выглядеть:

$A = begin a_ & … & a_ \ vdots & … & vdots \ a_ & … & a_ end$, $b=begin b_1 \ vdots \ b_m end$

Если через длинную черту после матрицы множителей при неизвестных записан столбец свободных членов, то матрицу называют расширенной матрицей системы.

Видео:ФСР системы линейных уравнений. Алгоритм ГауссаСкачать

Необходимая терминология

Решением системы называют такие $n$ значений неизвестных $x_1=c_1, x_2=c_2…x_n-c_n$, что при их использовании все её уравнения становятся верными соблюдающимися равенствами. Найденное решение системы можно записать в виде таблицы неизвестных одним столбцом:

$C= begin c_1 \ c_2 \ vdots \ c_n end$.

В зависимости от количеств групп переменных, подходящих для соблюдения всей системы, различают совместные и несовместные СЛАУ. Объединённая в систему группа равенств называется совместной, если она имеет хотя бы одно решение и несовместной, если она не имеет решений.

Готовые работы на аналогичную тему

Среди первого типа существуют определённые СЛАУ, имеющие только одно решение и неопределённые, под такие подпадают все, которые можно решить с получением больше одного ответа.

Видео:Фундаментальная система решений видео-урок!Скачать

Однородные и неоднородные системы линейных уравнений

Система линейных уравнений называется однородной, если все её свободные члены равны нулю. Если в системе хотя бы один из свободных членов ненулевой, то она называется неоднородной, другие же СЛАУ с нулевым $B$ наоборот однородны.

Однородные системы совместны, так как $x_1=x_2=. x_n=0$ будет решением для систем, имеющих особенность в виде нулевого столбца $B$. Иначе такая группа ответов называется нулевым или тривиальным способом решения.

Нетривиальными же называются ответы на СЛАУ, детерминант матрицы которой не $0$. В группе ответов таких систем хотя бы одно из неизвестных подходит под $x_i$ ≠ $0$. Для поиска детерминанта можно воспользоваться $LU$ разложениями, гаусовым методом или его модификацией в виде способа Жордана-Гаусса.

Видео:Неоднородная система линейных уравненийСкачать

Общее, частное и фундаментальное решения

Частным решением системы называется индивидуальное записанное в одну строчку, тогда как общее $X_o$ записывается через свободные переменные в одну строчку, оно представляет собой некое множество чисел, подходящих под данные условия. Общее $X_o$ включает в себя все индивидуальные.

Фундаментальной же системой решений (ФСР) называется совокупность $(n-r)$ векторов, являющихся линейно независимыми векторами системы. Здесь $r$ — это ранг исследуемой матрицы, согласно теореме Капелли, он равен количеству её основных неизвестных. Найти его можно путём разрешённых преобразований над изучаемым объектом, в частности, можно использовать метод Гаусса или другие.

Фундаментальная система решений частенько представлена как сумма всех возможных решений:

Здесь $С_1, C_2. C_$ — некоторые постоянные.

Приведена пример, в котором все свободные члены ненулевые:

$begin x_1 – x_2 + x_3-x_4=4 \ x_1+x_2+2x_3+3x_4=8 \ 2x_1+4x_2+5x_3+10x_4=20 \ 2x_1-4x_2+x_3-6x_4=4\ end$.

Ранг всех матриц соответсвует двойке, рассчитаем базисный минор:

Избавимся от двух нижних равенств из примера и получим:

$begin x_1 – x_2=4-c_3+c_4 \ x_1+x_2=8-2c_3-3c_4 \ end$

Общим решением системы будет строчка $(6-fracc_3-c_4; 2-fracc_3-2c_4;c_3; c_4)$.

Теперь посмотрим, что буде в случае с нулевым столбцом за чертой:

$begin x_1 – x_2 + x_3-x_4=0 \ x_1+x_2+2x_3+3x_4=0 \ 2x_1+4x_2+5x_3+10x_4=0 \ 2x_1-4x_2+x_3-6x_4=0 end$.

Ранг также соответствует двойке, а её решениями будут

$c_1=-frac c_3-c_4; c_2=-fracc_3-2c_4$. Константы же $c_3$ и $c_4$ выберем любые, например, возьмём их равными $c_3=0;c_4=1$.

Итак, используя приведённые выше значения $c_3=0;c_4=1$:

Фундаментальное решение системы можно записать так:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 17 04 2022

Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Фундаментальная система решений

Содержание:

Одним из важнейших понятий в теории однородных систем линейных ОДУ является понятие фундаментальной системы решений.

Определение 5.2. Линейно независимую в промежутке систему из вектор-функций вида (5.7), каждая из которых является в нем решением однородной системы п линейных ОДУ (5.3), называют фундаментальной системой решений для (5.3) в этом промежутке.

Теорема 5.7. Фундаментальные системы решений существуют.

Пусть чисел

образуют единичную матрицу размера n, определитель которой Рассмотрим n решений однородной системы (5.3), которые определены в некотором промежутке числовой прямой точке удовлетворяют начальным условиям Тогда получим в промежутке Т.

На основании теоремы 5.5 и определения 5.1 отсюда следует, что эти решения линейно независимы в промежутке Т и, согласно определению 5.2, образуют в нем фундаментальную систему решений для (5.3).

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Запись в виде (5.3) соответствует нормальной однородной системе линейных ОДУ с переменными коэффициентами, поскольку элементы матрицы A(t) этой системы являются функциями независимого переменного t.

• Такие системы удается проинтегрировать и получить решение в виде аналитической зависимости лишь в исключительных случаях. Однако существует одна замечательная формула, связывающая между собой решения произвольной однородной системы (5.3) ОДУ с переменными коэффициентами.

Вычислим производную по t от определителя Вронского (5.6), составленного из решений системы ОДУ (5.3):

В (5.8) использовано правило вычисления производной от определителя квадратной матрицы размера п [II]. Так как определитель представляет собой сумму слагаемых с соответствующими знаками, а каждое слагаемое есть произведение п элементов, то, используя правило дифференцирования произведения п функций [II], приходим к записи (5.8). Вектор-функция является решением однородной системы (5.3), т.е. Поэтому первый определитель в правой части (5.8) имеет вид

Здесь использовано правило сложения определителей, а также то, что определитель, имеющий две одинаковые строки, равен нулю.

Возможно вам будут полезны данные страницы:

Аналогично второе, третье и т.д. (вплоть до последнего) слагаемые в (5.8) равны: С учетом этих выражений (5.8) принимает вид Отсюда следует, что определитель Вронского удовлетворяет линейному однородному ОДУ первого порядка с разделяющимися переменными. Разделяя переменные и интегрируя, получаем соотношение которое называют формулой Остроградского — Лиувил-ля (Ж. Лиувилль (1809-1882) — французский математик и механик, а о русском математике и механике М.В. Остроградском (1801-1861) см. Краткий исторический очерк.

Пример с решением №1

Рассмотрим нормальную систему ОДУ где — произвольная функция, непрерывная в некотором промежутке .

Решение:

Матрица этой системы Отсюда следует, что и формула Остроградского — Лиувилля принимает вид где

Итак, для двух произвольных решений рассматриваемой системы справедливо (5.11). Отметим, что (5.11) можно использовать для контроля точности получаемых решений системы

ОДУ при ее численном интегрировании

ОПРЕДЕЛЕНИЕ. Система m линейных уравнений с п переменными называется однородной, если во всех ее уравнениях свободные члены равны нулю.

В общем случае однородная система (или система однородных уравнений) имеет вид:

Система линейных однородных уравнений всегда совместна, так как она всегда имеет, по крайней мере, нулевое (тривиальное) решение (0; 0; 0). Действительно, набор значений неизвестных

удовлетворяет всем уравнениям системы.

ОПРЕДЕЛЕНИЕ. По отношению к системе (1.25) система (1.34) называется приведенной.

Если в системе (1.34) то она имеет только одно нулевое решение (см. теорему 1.7).

ТЕОРЕМА 1.11. Система линейных однородных уравнений имеет ненулевое решение тогда и только тогда, когда ранг этой системы меньше числа ее неизвестных, т.е. при

Следствие 1. Если число уравнений однородной системы меньше числа ее неизвестных, то эта система имеет ненулевое решение. Следствие 2. Если в однородной системе число уравнений равно числу неизвестных, то она имеет ненулевое решение тогда и только тогда, когда определитель матрицы системы равен нулю.

Обозначим решение системы (1.34) в виде строки

Решения системы линейных однородных уравнений обладают следующими свойствами:

1. Если строка — решение системы (1.34), то и строка — также решение этой системы.

2. Если строки — решения системы (1.34), то при любых с> и с2 их линейная комбинация — также решение данной системы.

Убедиться в справедливости указанных свойств решений системы линейных однородных уравнений можно непосредственной подстановкой их в уравнения системы.

Из сформулированных свойств следует, что всякая линейная комбинация решений системы линейных однородных уравнений также является решением этой системы. Поэтому целесообразно найти такие линейно независимые решения системы (1.34), через которые линейно выражались бы все остальные ее решения.

ОПРЕДЕЛЕНИЕ. Система линейно независимых решений называется фундаментальной, если каждое решение системы (1.34) является линейной комбинацией решений

ТЕОРЕМА 1.12. Если ранг г матрицы однородной системы линейных уравнений (1.34) меньше числа неизвестных n, то всякая ее фундаментальная система решений состоит из решений (или матрица фундаментальной системы имеет столбцов).

Поэтому общее решение системы (1.34) линейных однородных уравнений имеет вид:

(1.35)

где —любая фундаментальная система решений; — произвольные числа и Замечание. Общее решение системы линейных уравнений с п неизвестными (1.25) равно сумме общего решения соответствующей ей приведенной системы линейных уравнений (1.34) и произвольного частного решения этой системы (1.25).

Для нахождения фундаментальной системы решений предположим, что ранг Тогда базисные неизвестные этой системы линейно выражаются через свободные переменные Положим значения свободных переменных Затем находим второе решение, принимая Иными словами, мы последовательно присваиваем каждой свободной переменной единичное значение, положив остальные нулями.

Пример с решением №2

Найти решение и фундаментальную систему решения системы линейных однородных уравнений: Решение:

Составим матрицу системы, и прямым ходом метода Гаусса приведем ее к ступенчатому виду:

Выпишем систему уравнений: Обратный ход метода Гаусса дает значения базисных неизвестных выраженные через свободную переменную . Обозначим ее

Из последнего уравнения находим Затем, поднимаясь вверх по системе, определяем все неизвестные

Эти последние выражения представляют запись общего решения нашей однородной системы. Если теперь давать переменной с числовые значения, можно получить фундаментальное решение системы.

Поскольку ранг однородной системы равен четырем, то фундаментальная система решений для нее состоит из решения.

Положив значение свободной переменной (других свободных переменных у нас нет), получим фундаментальное решение системы:

Заметим, что если и решением будет нулевой вектор о; его называют тривиальным решением; этот вектор всегда есть среди решений однородной системы.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

💥 Видео

Фундаментальная система решений для однородной системы линейных уравненийСкачать

Математика без Ху!ни. Метод Гаусса.Скачать

Решение системы уравнений методом ГауссаСкачать

Аржанцев И. В. - Алгебра. Часть 1 - Фундаментальная система решенийСкачать

Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Математика это не ИсламСкачать

Лекция 13. Исследование систем линейных уравнений. Теорема Кронекера — Капелли.Скачать

Базисные решения систем линейных уравнений (03)Скачать

Решение неоднородных линейных систем. ТемаСкачать

Теорема о существовании фундаментальной системы решений системы линейных однородных уравнений.Скачать

Собственные векторы и собственные числа линейного оператораСкачать

Решение системы дифференциальных уравнений методом ЭйлераСкачать