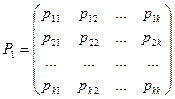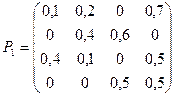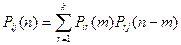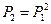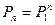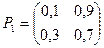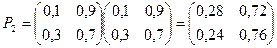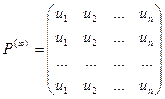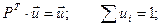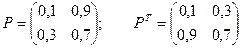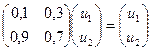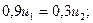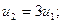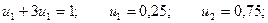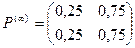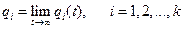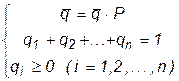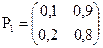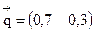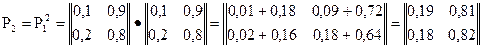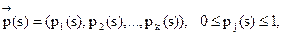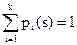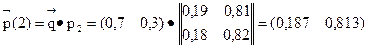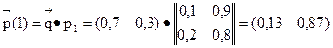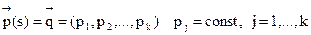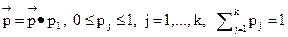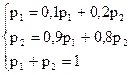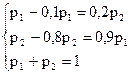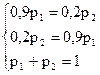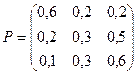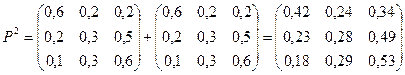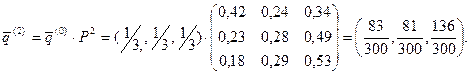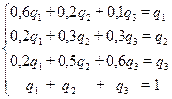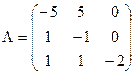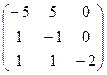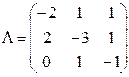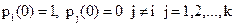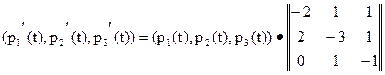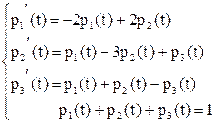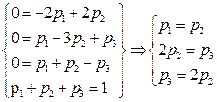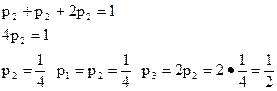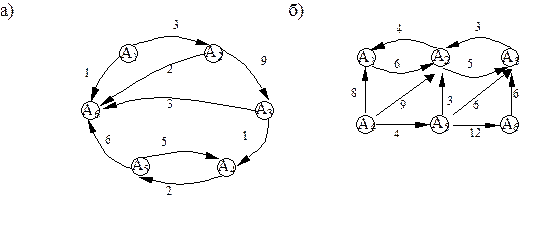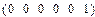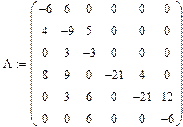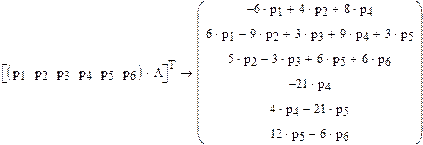Размеченный граф состояний вектор вероятностей

Определение. Случайный процесс с дискретным временем называется марковским, если на любом шаге S вероятность P (S) перехода системы из состояния i , в состояние jзависитлишь от состояния А в которое попала система на (S—1) шаге, и не зависит от того, как и когда она в это состояние попала. Кратко это свойство формулируют так: при задан­ном настоящем будущее не зависит от прошлого. В силу это­го марковский процесс еще называют процессомбез после­действияили однородным.

Определение. Цепью Маркова называется последовательность испытаний, в каждом из которых появляется только одно из k несовместных событий A_i из полной группы. При этом условная вероятность p_ij(s) того, что в s –ом испытании наступит событие A_j при условии, что в (s – 1) – ом испытании наступило событие A_i, не зависит от результатов предшествующих испытаний.

Независимые испытания являются частным случаем цепи Маркова. События называются состояниями системы, а испытания – изменениями состояний системы.

По характеру изменений состояний цепи Маркова можно разделить на две группы.

Определение. Цепью Маркова с дискретным временемназывается цепь, изменение состояний которой происходит в определенные фиксированные моменты времени. Цепью Маркова с непрерывным временемназывается цепь, изменение состояний которой возможно в любые случайные моменты времени.

Определение. Однороднойназывается цепь Маркова, если условная вероятность p_ij перехода системы из состояния i в состояние j не зависит от номера испытания. Вероятность p_ij называется переходной вероятностью.

Пусть, число состояний конечно и равно k.

Тогда матрица, составленная из условных вероятностей перехода будет иметь вид:

Эта матрица называется матрицей перехода системы.

Т.к. в каждой строке содержаться вероятности событий, которые образуют полную группу, то сумма элементов каждой строки матрицы равна единице.

На основе матрицы перехода системы можно построить граф состояний системы,или размеченный граф состояний.

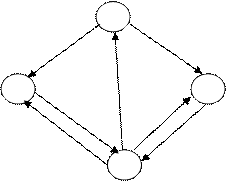
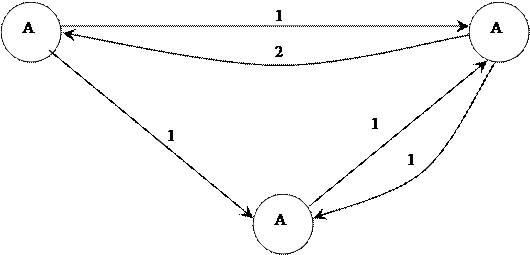
Пример. По заданной матрице перехода построить граф состояний.

Т.к. матрица четвертого порядка, то, соответственно, система имеет 4 возможных состояния.

На графе не отмечаются вероятности перехода системы из одного состояния в то же самое.

Пусть P_ij(n) – вероятность того, что в результате n испытаний система перейдет из состояния i в состояние j, r – некоторое промежуточное состояние между состояниями i и j. Вероятности перехода из одного состояния в другое p_ij(1) = p_ij.

Тогда вероятность P_ij(n) может быть найдена по формуле, называемой равенством Маркова:

Здесь т – число шагов (испытаний), за которое система перешла из состояния i в состояние r.

Равенство Маркова можно трактовать как видоизмененную формулу полной вероятности.

Используя матрицу перехода Р₁, можно найти вероятности P_ij(2) перехода из состояния i в состояние j за два шага , т.е. матрицу Р₂:

так как при n=2 равенство Маркова – формула умножения матрицы P₁ на P₁ , следовательно, можно получить:

Пример. Задана матрица переходов Р₁. Найти матрицу Р2.

Определение. Матрицы, суммы элементов всех строк которых равны единице, называются стохастическими.

Если при некотором п все элементы матрицы Р п не равны нулю, то такая матрица переходов называется регулярной.

Регулярные матрицы переходов задают цепь Маркова, в которой каждое состояние может быть достигнуто через п шагов из любого состояния. Такие цепи Маркова также называются регулярными.

Теорема. (теорема о предельных вероятностях) Пусть дана регулярная цепь Маркова с п состояниями и Р – ее матрица вероятностей перехода. Тогда существует предел 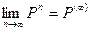и матрица Р ( ¥) имеет вид:

Т.о. матрица Р ( ¥) состоит из одинаковых строк. Числа u₁, u₂, …, u_n называются предельными вероятностями.Эти вероятности не зависят от исходного состояния системы и являются компонентами собственного вектора матрицы Р Т (транспонированной к матрице Р).

Собственный вектор полностью определяется из условий:

Пример. Найдем предельные вероятности для рассмотренного выше примера.

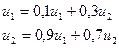
C учетом того, что u₁ + u₂ = 1, получаем:

Итак:

Возможные состояния системы в момент t=m можно охарактеризовать векторами 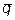(m) =(q₁ (m) , q₂ (m) , . q_k (m) ),

где q_i (m) – это вероятность того, что в момент t=m система находится в состоянии А_i.

Используя формулу полной вероятности, нетрудно показать, что имеет место равенство:

(m+1) = (m) ×Р.

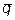
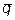
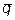
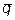
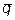
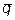
Применяя эту формулу последовательно при m=0, 1, 2. , можно получить выражение для вектора (m) через вектор начальных состояний (0) и матрицу вероятностей переходов Р, а именно:

(m)= (0) × Р m .

Предельным распределением вероятностей цепи Маркова называется вектор q p =<q₁, q₂, . q_k> такой, что

Стационарным распределением называется вектор q=<q₁, q₂, . q_k>, который удовлетворяет условиям:

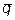
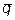
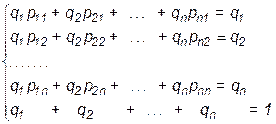
Вектор определяет распределение вероятностей, которое с течением времени не меняется, т.е. стационарное распределение является также предельным распределением. В развернутом виде система для нахождения координат вектора , т.е. имеет следующий вид:

(*)

Первые n уравнений этой системы являются линейно зависимыми, поэтому любое одно из них можно отбросить. В результате получится система n линейных уравнений, которая почти всегда имеет единственное решение.

По теореме о предельных вероятностях регулярная цепь Маркова имеет предельное распределение вероятностей, которое может быть найдено из системы (*).

Задача 1. Задана матрица P₁ вероятностей перехода дис­кретной цепи Маркова из i-ro в j-oe состояние за один шаг (i, j = 1, 2). Распределение вероятностей по состояниям в началь­ный момент t = 0 определяется вектором .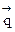

1) матрицу P₂ перехода цепи из состояния i в со­стояние j за два шага;

2) распределение вероятностей по состоя­ниям в момент t = 2;

3) вероятность того, что в момент t = 1 со­стоянием будет i = 2;

4) стационарное распределение.

Решение: Для дискретной цепи Маркова в случае её однородности справедливо соотношение ,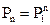

где P₁ – матрица переходных вероятностей за один шаг

P_n – матрица переходных вероятностей за n шагов;

1) Найдем матрицу P₂ перехода за 2 шага.

Пусть распределение вероятностей по состояниям на S-ом шаге определяется вектором

Зная матрицу P_n перехода за n шагов можно определить распределение вероятностей по состоянием на (s+n)-ом шаге.

,

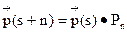
2) Найдем распределение вероятностей по состоянием системы в момент t=2. Положим (4) S=0 и n=2. Тогда .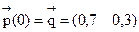

Получим

3) Найдем распределение вероятностей по состояниям системы в момент t=1. Положим в (4) S(0) и n=1, тогда

Откуда видно, что вероятность того, что в момент t=1 состоянием цепи будет A₂, равна p₂(1)=0,87.

Распределением вероятностей по состояниям называется стационарным, если оно не меняется от шага к шагу, то есть

Тогда из соотношения (4) при n=1 получим 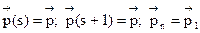или

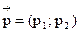
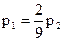
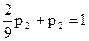
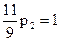
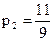
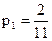
4) Найдем стационарное распределение. Так как k=2 имеем . Запишем систему линейных уравнений (5) в координатной форме:

; ; ; ; .

Следовательно, .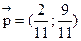

1) матрица перехода за два шага для данной цепи Маркова имеет вид ;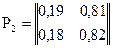

2) распределение вероятностей по состояниям в момент t=2 равно ;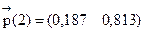

3) вероятность того, что в момент t=1 состоянием цепи будет A₂, равна p₂(1)=0,87;

4) Стационарное распределение имеет вид .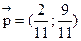

Задача 2. Ремонтная мастерская располагает двумя диагностическими приборами. Известно, что если в какой-то день оба прибора были незаняты, то на следующий день с вероятностью 0,6 они снова окажутся незанятыми и с одинаковыми вероятностями будет занят один или два прибора. Если был занят один прибор, то назавтра с вероятностью 0,2 оба будут свободны и с вероятностью 0,5 – оба заняты. Наконец, если оба прибора были заняты, то назавтра с вероятностью 0,6 оба опять будут заняты и с вероятностью, вдвое меньшей, будет занят только один прибор. Предполагая, что в начале недели (в понедельник) нет никакой информации о занятости приборов, найти вероятность того, что в среду оба прибора будут заняты. Кроме того, найти предельное распределение вероятностей.

Решение. Рассмотрим следующие состояния:

Е₀ – не занят ни один прибор;

Исходя из условия задачи матрица вероятностей переходов имеет вид:

Отсутствие информации в понедельник фактически означает, что вероятности начальных состояний одинаковые, т.е.:

=(1/3; 1/3; 1/3).

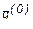
Вероятности состояний в среду определяются вектором q (2) .

Таким образом, вероятность занятости сразу двух приборов будет равна 136/300.

Предельные вероятности найдем как решение системы:

Решая эту систему методом Гаусса, найдем:

Марковские цепи с конечным числом состоянии и непрерывным временем

Пусть физическая система, возможные состояния которой А₁,А₂, . , А_k может переходить из со­стояния в состояние не в определенные моменты времени, а в любой момент времени случайным образом. При этом воз­никает случайный процесс (цепь) с непрерывным временем.

Если процесс с непрерывным временем обладает отсутствием последействия, то его называют марковским случайным процессом с непрерыв­ным временем или непрерывной цепью Маркова.

Для непрерывной цепи Маркова. вероятность перехода из состояния А_i в состояние А_j в любой момент времени равна нулю. Поэтому вместо вероятности перехода Р_ij рассматривают плотность вероят­ности перехода l_ij которая определяется как предел отно­шения вероятности перехода Р_ij за время Dt из состо­яния A_i в состояние A_j; к длине промежутка Dt при Dt 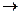0, т. е.

l_ij = 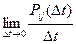. (1)

Плотность вероятности l_ij может быть как постоянной величиной, так и величиной, зависящей от момента времени t, с которого начинается промежуток Dt.

Если плотность ве­роятности перехода l_ij не зависит от t, марковский процесс(цепь) называетсяоднородным.

В дальнейшем будем пред­полагать, что рассматриваемые процессы удовлетворяют ус­ловиюординарности: в один и тот же момент времени t си­стема не может изменить свое состояние более чем один раз.

Из курса дифференциального исчисления известно, что соотношение (1) можно записать в виде Р_ij(Dt)=l_ijDt + a_ij(Dt), где a_ij(Dt)— бесконечно малая высшего порядка по сравнению с Dt. Тогда с точностью до бесконеч­но малой имеем:

P_ij(Dt) = l_ijDt, i 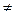j (2)

т. е. вероятность перехода Р_ij(Dt) за малое время Dt равна произведению плотности вероятности перехода l_ij на Dt. По­этому l_ij еще называютинтенсивностью перехода системы из А_i в Aj.

Из величин l_ij составим квадратнуюматрицу интенсивностей переходов:

L = 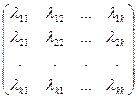(3)

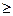
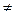
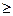
1) l_ij 0, i j, это следует из (2), так как P_ij(Dt) 0;

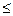
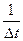
2) l_ij 0, i=j, так как l_ii = (P_ii(Dt) – 1);

3) = 0 действительно, (l_i1 + l_i2 + … l_ii + … l_ik)Dt = P_i1(Dt) + P_i2(Dt) +…+( P_ii(Dt) – 1) + …+ P_ik(Dt)) = 0.

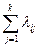
Интенсивности переходов l_ij удобно задавать на графе состояний. На графе указывают обычно интенсивности l_ij >0.

Зная матрицу интенсивностей переходов или размеченный граф состояний, можно определить вероятности состояний:

p₁ (t), p₂ (t), …, p_k(t), 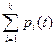= 1, (4)

т. е. вероятности нахождения системы в состоянии А₁, А₂, … , А_k в момент времени t. Вероятности p_i(t) как функции t удовлетворяютсистеме дифференциальных уравнении Колмо­горова, которая в матричной форме имеет вид

матрица интенсивностей переходов (З).

Распределение вероятностей состояний системы называетсястационарным, если оно не меняется с течением времени, т. е. если

где p = ( p₁, p₂, …, p_k) = const, j = 1, 2, . k. Дифференцируя равенство (6) по t, получим: p ’ (t) = 0.

С учетом уравнения (5) приходим к выводу, что стационар­ное распределение удовлетворяет соотно­шению

т. е. для получения стационарного распределения достаточно в системе дифференциальных уравнений Колмогорова поло­жить p ‘ _j =0; j =1, 2. k.

Уравнения системы (7) не в матричной форме удобно вы­писывать непосредственно по размеченному графику состоя­ний в соответствии со следующим правилом:

сумма произведений l_jip_i, j 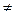i для стрелок, выходящих из i-го состояния, рав­на сумме произведений l_ijp_j, j iдля стрелок, входящих в i—е состояние.

Задача 2. Задана матрица

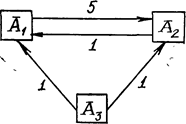
интенсивностей переходов непрерывной цепи Маркова. Со­ставить размеченный граф состояний, соответствующий мат­рице L; выписать систему дифференциальных уравнений Колмогорова для вероятностей состояний; найти стационар­ное распределение вероятностей.

Решение. Размеченный граф должен иметь 3 состояния А₁, А₂, А₃. Из матрицы L находим интенсивности переходов l_ij>0, i j и отмечаем их над соответствующими стрелка­ми (рис. 2). Имеем l₁₂=5, соединяем состояния А₁ и А₂ стрел­кой, направленной от А₁ к А₂, отмечая интенсивность перехода над стрелкой; l₁₃=0, следовательно, состояния А₁ и А₃ стрелкой не соединяем и т. д. Составляем

(p₁ ’ (t), p₂ ’ (t), p₃ ’ (t)) = (p₁(t), p₂(t), p₃(t))

умножая вектор p(t) на матрицу L будем иметь:

p₁ ’ (t) = — 5 p₁(t) + p₂(t) + p₃(t);

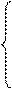
Для нахождения стационарного распределения достаточ­но в последней системе дифференциальных уравнений положить все производные p_i ’ (t ) = 0, i = 1, 2, 3. Пусть p = (p₁, p₂, p₃)есть стационарное распределение, тогда:

0 = — 5 p₁ + p₂ + p₃;

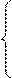
Решая систему, получим p₃ = 0, p₂= 5p₁. В силу уравнения (4) p₁ + p₂ + p₃ = 1,следовательно, p = ( 1/6; 5/6; 0).

Заметим, что для определения стационарного распределе­ния мы получили бы такую же систему, если бы воспользо­вались правилом, приведенным выше. Действительно, для состояния А₁ имеем 5 p_{1 =} 1 p₂ + 1 p₃ , для состояния А₂: 1 p₂ = 5p₁ + 1 p₃, для состояния A₃: 1 p₃ + 1p₃ = 0. Составляя из этих уравнений систему, убедимся, что она эквивалентна си­стеме(8).

Для многих практических случаев важно знать, как ведут себя вероятности p_i(t>, i=l, 2. k при большом времени работы системы, т. е. при t 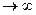. Если при определенных ус­ловиях существуютпредельные вероятности состояний

p_i = 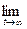p_i(t), i = 1, 2, …, k, (9)

не зависящие от того, в каком состоянии система находилась в начальный момент, то это означает, что с течением времени в системе устанавливаетсяпредельный стационарный режим.

Система, для которой существуют предельные вероятно­сти, называетсяэргодической, а возникающий в ней случай­ный процессэргодическим.

Выясним условия, при которых существуют предельные вероятности состояний. Введем ряд понятий.

Состояние А_i называетсянесущественным, если найдется такое состояние А_j что из A_i в А_j, перейти можно, а из Aj в A_i — нельзя. Состояние A_i называетсясущественным,если оно не является несущественным. Например, для систе­мы, граф состояний которой дан на рис. 2, состояние А₃ не­существенно (так как из него можно перейти в состояние А₁или А₂ но обратно вернуться нельзя), состояния А₁ и A₂ — существенны. Два существенных состояния A_i и A_j назы­ваютсясообщающимися, если из A_i можно попасть в A_j и из A_j в A_i. На рис. 2 представлены сообщающиеся состоя­ния A₁ и А₂.

Теорема 1. Если A_i — несущественное состояние, то

p_i(t) = 0. (10)

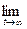
Смысл этой теоремы состоит в том, что в конечном итоге система выйдет из несущественного состояния A_i и больше в него не вернется.

Теорема 2. Чтобы цепь (процесс) с конечным числом состояний имела единственное стационарное распределение вероятностей, совпадающее с предельным, необходимо и до­статочно, чтобы все ее существенные состояния сообщались между собой.

Пример. В условиях задачи 2 найти предельные веро­ятности состояний.

Решение. В рассматриваемой цепи состояния A₁ и A₂ являются существенными сообщающимися состояниями, A₃ — несущественно. Следовательно, по теореме 2 предель­ное распределение совпадает со стационарным и имеет вид p = ( 1/6; 5/6; 0). Заметим, что результат 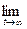p₃(t) = 0 можно было получить непосредственно из теоремы 1, так как состояние A₃ несущественно.

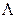
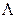
Пример. Задана матрица интенсивностей переходов непрерывной цепи Маркова. Составить размеченный граф со­стояний, соответствующий матрице ; составить систему диф­ференциальных уравнений Колмогорова для вероятностей состояний; найти предельное распределение вероятностей.

Решение: Однородная цепь Маркова с конечным числом состояний A₁,A₂,…,A_k характеризуется матрицей интенсивностей переходов

,

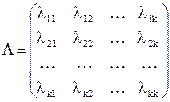
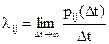
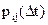
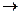
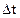
где — интенсивность перехода цепи Маркова из состояния A_i в состояние A_j;

— вероятность перехода A_i A_j за интервал времени .

Переходы системы из состояния в состояние удобно задавать с помощью размеченного графа состояний, на котором отмечаются дуги, соответствующие интенсивностям .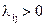

Составим размеченный граф состояний для заданной матрицы интенсивностей переходов.

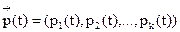
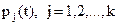
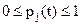
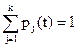
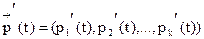
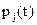
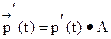
Пусть — вектор вероятностей , нахождения системы в состоянии A_j в момент t. Очевидно, что и . Тогда по правилу дифференцирования векторной функции скалярного аргумента получим . Вероятности удовлетворяют системе дифференциальных уравнений Колмогорова (СДУК), которая в матричной форме имеет вид

,

Если в начальный момент система находилась в состоянии A_j, то СДУК следует решать при начальных условиях

Совокупность СДУК (6) и начальных условий (7) однозначно описывает однородную цепь Маркова непрерывным временем и конечным числом состояний.

Составим СДУК для заданной цепи Маркова. Поскольку k=3, то j=1,2,3. Из соотношения (6) получим

Отсюда будем иметь:

Последнее условие называется нормировочным.

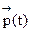
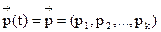
Распределение вероятностей по состояниям называется стационарным, если оно не меняется с течением времени, то есть , где p_j=const, j=1,2,…,k.

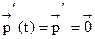
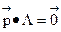
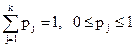
Отсюда . Тогда из СДУК (6) получаем систему для нахождения стационарного распределения , где .

Для данной задачи из СДУК будет иметь

Из нормировочного условия получим

Ответ: предельное распределение имеет вид .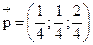

Пример. Определить, существует ли стационарный режим для марковского случайного процесса, размеченный граф состояний которого изображен на рисунке. Если стационарный режим существует, то найти стационарное распределение вероятностей.

Указание.Проведите классификацию состояний системы и примените следствия из теоремы Маркова.

а) Состояние 6 — существенное. Остальные — несущественные состояния. Поэтому единственное стационарное распределение совпадает с предельным.

Для несущественных состояний предельные вероятности равны нулю. Учитывая, что сумма всех вероятностей = 1 получим искомое стационарное распределение:

б) Несущественные состояния 1, 2, 6. Состояния 3, 4, 5 — существенные сообщающиеся поэтому единственное стационарное распределение совпадает с предельным.

Приравнивая к каждую из строк-уравнений к 0 и учитывая, что сумма вероятностей = 1 получим:

Видео:Графы, вершины, ребра, инцидентность, смежностьСкачать

Тема 5. Случайные процессы с дискретными состояниями и непрерывным временем.
Статистическое моделирование экономических систем
(метод Монте-Карло)

Оглавление

Видео:теория вероятности ГРАФЫ математикаСкачать

Вступление

На прошлой лекции мы начали рассматривать вероятностные модели.

Первая группа моделей, которые мы рассмотрели, относится к системам с конечным числом состояний, в которых переходы из состояния в состояние осуществляются в дискретные моменты времени (заранее заданные и, как правило, с равными промежутками).

С такими системами связывается матрица переходных вероятностей. Если эти вероятности постоянны (не зависят от времени), то цепь Маркова называется однородной. Кроме этого должен быть задан вектор начальных вероятностей.

Была дана формула, которая позволяет получить вектор вероятностей оказаться в том или ином состоянии после k-го шага функционирования процесса.

Видео:Графы и их применение | Теория ВероятностиСкачать

Непрерывные цепи Маркова

Теперь рассмотрим процессы, в которых переход из узла в узел (из состояния в состояние) может произойти через любой случайный промежуток времени.

В этом случае мы должны ввести в рассмотрение непрерывное время, чтобы отслеживать (ловить) эти случайные моменты срабатывания переходов.

Марковский случайный процесс с дискретными состояниями и непрерывным временем называется при условии, что переход системы из состояния в состояние происходит не в фиксированные, а в случайные моменты времени.

Примеры

Поступление заявок на выполнение банковских операций.

Поломка машины в дороге.

Задание системы с конечным числом состояний и непрерывным временем наступления события (перехода из состояния в состояние)

Пусть система характеризуется n состояниями S₀, S₁, S₂. S_n, а переход из состояния в состояние может осуществляться в любой момент времени. Обозначим через P_i(t) вероятность того, что в момент времени t система S будет находиться в состоянии S_i (i = 0,1. n). Требуется определить для любого t вероятности состояний P₀(t), P₁ (t), …P_n(t). Очевидно, что

Определение плотности вероятностей перехода

Для процесса с непрерывным временем вместо переходных вероятностей Р_ij рассматриваются плотности вероятностей перехода λ_ij, представляющие собой предел отношения вероятности перехода системы за время из состояния S_i в состояние S_j к длине промежутка :

Если λ_ij=const, то процесс называется однородным.

Если плотность вероятности λ_ij(t), то процесс — неоднородный.

При рассмотрении непрерывных марковских процессов принято представлять переходы системы S из состояния в состояние как происходящие под влиянием некоторых потоков событий.

Потоки событий

Поток событий – последовательность однородных событий, следующих одно за другим в какие-то случайные моменты времени.

В предыдущем примере – это поток отказов машины и поток восстановлений. Другие примеры: поток заявок в банкомат, поток покупателей в магазине, поток документов и т. д.

Поток событий можно наглядно изобразить рядом точек на оси времени Ot (рис. 1).

Рис. 1

Положение каждой точки случайно, и здесь изображена лишь какая-то одна реализация потока.

Интенсивность потока событий (λ) – это среднее число событий, приходящееся на единицу времени.

Пусть задан момент времени t и промежуток времени .

Обозначим – среднее число событий на промежутке .

Тогда .

Свойства потока событий

Рассмотрим некоторые свойства (виды) потоков событий.

Различают следующие основные свойства, которыми могут обладать случайные потоки событий:

• стационарность;
• ординарность;
• отсутствие последействия.

Стационарность

Свойство стационарности проявляется в том, что вероятность попадания того или иного числа событий на участок времени зависит только от длины участка и не зависит от расположения на оси 0t (времени). Другими словами, стационарность означает неизменность вероятностного режима потока событий во времени. Поток, обладающий свойством стационарности, называют стационарным. Для стационарного потока среднее число событий, воздействующих на систему в течение единицы времени, остается постоянным.

В частности, интенсивность стационарного потока постоянна λ=const. Поток событий неизбежно имеет сгущения или разрежения, но они не носят закономерного характера, и среднее число событий, приходящееся на единицу времени, постоянно и от времени не зависит.

Поток событий называется стационарным, если его вероятностные характеристики не зависят от времени.

Реальные потоки событий в экономике предприятия являются в действительности стационарными лишь на ограниченных участках времени. Поэтому, чтобы применить свойство стационарности, модели исследуют на ограниченных участках времени.

Ординарность

Свойство ординарности потока присутствует, если вероятность попадания на элементарный участок времени двух и более событий пренебрежимо мала по сравнению с длиной этого участка. Свойство ординарности означает, что за малый промежуток времени практически невозможно появление более одного события. Поток, обладающий свойством ординарности, называют ординарным.

Можно сказать, что для любого t на сколь угодно малом промежутке два события не произойдут.

Поток событий называется ординарным, если события в нем появляются поодиночке, а не группами по нескольку сразу. Иначе говоря, два события не происходят в один и тот же момент времени. Например, две машины не подъедут одновременно к стоянке, два человека не подойдут к банкомату, не обратятся с запросом к одной и той же БД и т.д.

За промежуток времени что может произойти?

• ни одного события;
• 1 событие;
• > 1 события.

Если рассмотреть очень маленький промежуток времени (0), то на нем можно выписать вероятности, которые зависят от времени t и от :

– вероятность того, что ничего не случится;

– вероятность, что случится 1 событие;

– вероятность, что случится больше 1-го события.

По природе вероятности можно записать

Последним слагаемым пренебрегаем в виду его малости.

Можно сформулировать свойство ординарности таким образом: для любого момента времени t можно указать две вероятности: (ничего не произойдет), (произойдет 1 событие)

Реальные потоки событий в различных экономических системах либо являются ординарными, либо могут быть достаточно просто приведены к ординарным.

Для ординарных потоков интенсивность (математическое ожидание числа событий в единицу времени) (число событий может быть либо 0, либо 1)

Таким образом, интенсивность потока – это вероятность появления одного события на бесконечно малом промежутке времени. На практике интенсивность замеряют на некотором конечном промежутке времени и она приводится к этому промежутку.

Отсутствие последействия

Данное свойство потока состоит в том, что для любых непересекающихся участков времени ₁ и ₂(см. рис. ниже) число событий, попадающих на один из них, не зависит от того, сколько событий попало на другой. Другими словами, это означает, что события, образующие поток, появляются в те или иные моменты времени независимо друг от друга и вызваны каждое своими собственными причинами. Иначе говоря, количество событий, попадающих на один из них, не зависит от того, сколько событий попало на другие участки времени. Поток, обладающий свойством отсутствия последействия, называют потоком без последействия.

Например, поставили сачок в двух местах реки. Можно ли утверждать, что если в первый сачок поймали 10 рыб, то и во второй попадутся 10 рыб?

Простейший поток

Поток событий называется простейшим (или стационарным пуассоновским), если он обладает сразу тремя свойствами:

• стационарен;
• ординарен;
• не имеет последействия.

Простейший поток имеет наиболее простое математическое описание. Он играет среди потоков такую же особую роль, как и закон нормального распределения среди других законов распределения. А именно, при наложении достаточно большого числа независимых, стационарных и ординарных потоков (сравнимых между собой по интенсивности) получается поток, близкий к простейшему.

Если поток событий не имеет последействия, ординарен, но не стационарен, то его называют нестационарным пуассоновским потоком, а его интенсивность зависит от времени, т. е. .

Если поток событий удовлетворяет описанным выше свойствам, то справедлива теорема Цинлара.

Теорема. Пусть <N (t), > – простейший поток событий. Пусть некоторый фиксированный интервал времени. Тогда количество событий k, приходящихся на промежуток, является случайной величиной с распределением Пуассона, имеющим параметр a = (), т.е.

а — среднее число событий, приходящееся на промежуток времени.

Для простейшего потока , где – длина участка времени; – интенсивность потока:

Отметим еще одно важное свойство простейшего потока событий. Промежуток времени t между соседними событиями распределен по показательному закону, а его среднее значение T и среднее квадратичное отклонение равны.

Для простейшего потока с интенсивностью λ=const интервал T между соседними событиями имеет так называемое показательное (экспоненциальное) распределение с плотностью

Для случайной величины T, имеющей показательное распределение, математическое ожидание m_T есть величина, обратная параметру, а среднее квадратичное отклонение σ_T равно математическому ожиданию

Если в системе все потоки пуассоновские, то процесс, протекающий в системе S, будет марковским. И к нему применима теория непрерывных цепей Маркова.

Задача

Банкомат обслуживает одного человека в среднем 2 мин. К банкомату подходит в среднем 20 чел/ч. Считая поток клиентов к банкомату и поток выдачи денег из банкомата простейшими пуассоновскими, определить интенсивности этих потоков в одних единицах измерения (единиц/мин).

– интенсивность потока клиентов к банкомату = 1/3 чел/мин;

μ – интенсивность потока выдачи денег = 0,5 операции/мин.

Модель 8. Гараж-непрерывный

Автомобиль может находиться в двух состояниях – Исправен S₁ или Ремонт S₂. Поток событий, при котором автомобиль переходит из состояния Исправен в состояние Ремонт, является простейшим и характеризуется заданной интенсивностью λ, которую можно трактовать как количество поломок (отказов) в единицу времени. Поток восстановлений автомобиля также является простейшим и характеризуется заданной интенсивностью µ, которую можно трактовать как количество отремонтированных машин в единицу времени.

Рис. 2

Интенсивность потока отказов – λ.

Интенсивность потока восстановлений – μ.

Введем вектор вероятностей наступления событий

Начинаем выписывать производные:

Поясним смысл слагаемых в правой части этих выражений.

Событие (состояние) S₁ наступает за счет того, что осуществляется переход из узла (состояния) S₂ с интенсивностью μ, таким образом 1-е слагаемое показывает приращение вероятности, а уменьшение вероятности происходит от того, что осуществляется обратный переход к другому узлу с интенсивностью.

Пояснение на примере автомобиля. p₁(t)– вероятность того, что автомобиль исправен, может быть определено как отношение промежутка нахождения в исправном состоянии на общее время протекания процесса. Что увеличивает промежуток исправного состояния? Переход из неисправного состояния в исправное с интенсивностью μ. А что уменьшает этот промежуток? Соответственно, обратный переход с интенсивностью. Если автомобили ломаются и чинятся с одинаковой интенсивностью, то можно предположить, что вероятности нахождения в обоих состояниях будут равны 1/2.

Если автомобили ломаются часто, а ремонт происходит медленно, то вероятность быть в неисправном состоянии будет больше чем в исправном.

Таким образом, изменение вероятности p₁(t) (т. е. производная функции) увеличивается за счет выхода из ремонта и уменьшается за счет нахождения в ремонте. Это и отражают слагаемые в 1-м уравнении (соответственно со знаком «+» и «–»).

p₂(t) – вероятность того, что автомобиль неисправен, может быть определено как отношение времени неисправного состояния на общее время протекания процесса.

Если сложим эти равенства, то получим

Интегрируя ДУ, получим, .

Если забудем, что функции – это вероятности, то получим систему ДУ, которые можно решить и получить законы вероятности нахождения в состояниях.

Одно из ДУ можно заменить соотношением вида, т. е., например, решать такую систему уравнений

Что может интересовать исследователя при решении таких ДУ?

Например, устойчивые решения, т. е. параметры, при которых имеют место устойчивые решения. То есть если есть устойчивое решение, то переходные процессы заканчиваются и, начиная с некоторого T*, функции p₁(t),p₂(t) выходят на стационарное значение (финальная вероятность).

Таким образом исследователя может интересовать, можно ли заранее предсказать, что система выйдет на стационар. И если да, то чему он будет равен.

Другое направление исследования – это собственно сами эти переходные процессы.

Если в рассмотренном примере считать, что описаны два возможных состояния автомобиля, то можно определить подвижной состав для автопредприятия. Та же ситуация с оборудованием, со штатным составом сотрудников и пр.

Уравнения Колмогорова

Пусть система характеризуется n состояниями S₀, S₁, S₂. S_n, а переход из состояния в состояние может осуществляться в любой момент времени и является простейшим потоком событий. Обозначим через Р_i(t) вероятность того, что в момент времени t система S будет находиться в состоянии S_i(i = 0,1. n). Требуется определить для любого t вероятности состояний P₀(t), P₁ (t), …P_n(t).

Прежде всего, построим граф состояний системы.

Итак, на систему, находящуюся в состоянии S_i, действует простейший поток событий. Как только появится первое событие этого потока, происходит «перескок» системы из состояния S_i в состояние S_j(на графе состояний по стрелке S_iS_j).

Для наглядности на графе состояний системы у каждой дуги проставляют интенсивности того потока событий, который переводит систему по данной дуге (стрелке). λ_ij– интенсивность потока событий, переводящий систему из состояния S_i в S_j. Такой граф называется размеченным.

Уравнения Колмогорова представляют собой систему ДУ для определения вероятностей P_i(t)

Слагаемые вида , которые входят в систему со знаками «+» и «–», называются потоком вероятности перехода. При этом λ_ij могут быть постоянными или зависящими от времени.

Производная вероятности каждого состояния равна сумме всех потоков вероятности, идущих из других состояний в данное, и минус сумма всех потоков вероятности, идущих из данного состояния в другие.

Сформулируем мнемоническое правило, по которому в ДУ включаются те или иные слагаемые и те или иные знаки.

К этой системе можно добавить нормирующее уравнение:

Это уравнение дает возможность составить на одно ДУ меньше.

Систему можно решить вручную или с помощью компьютера.

Если записать ДУ Колмогорова для системы «Гараж», то получатся именно такие уравнения, которые мы выписали исходя из эмпирических рассуждений.

Финальные вероятности состояний

Если процесс, протекающий в системе, длится достаточно долго, то имеет смысл говорить о предельном поведении вероятностей P₁ (t), P₂ (t)… при .

Что будет происходить с вероятностями состояний при ? Будут ли P₁ (t), P₂ (t)… стремиться к каким-либо пределам? Если эти пределы существуют и не зависят от начального состояния системы, то они называются финальными вероятностями состояний.

где n – конечное число состояний системы.

Финальные вероятности состояний – это уже не переменные величины (функции времени), а постоянные числа. Очевидно, что

Говорят, что в системе S устанавливается предельный стационарный режим, в ходе которого она переходит из состояния в состояние, но вероятности состояний уже не меняются. Система, для которой существуют финальные вероятности, называется эргодической, а соответствующий случайный процесс — эргодическим.

Финальные вероятности состояний (если они существуют) могут быть получены путем решения системы линейных алгебраических уравнений, которые получаются из дифференциальных уравнений Колмогорова, если приравнять производные к нулю, а вероятностные функции состояний P₁(t), P₂(t)… в правых частях уравнений заменить соответственно на неизвестные финальные вероятности p ₁, p ₂ …

Финальная вероятность состояния S_i – это, по существу, среднее относительное время пребывания системы в этом состоянии.

Сделать предположения, что будет с системой, в некоторых случаях можно по графу

Пример 1.

Например, рассмотрим граф системы:

Здесь мы видим однонаправленное движение (ухудшение или улучшение). Глядя на граф можно сказать, что в будущем система обязательно скатится в состояние 4, 5 или 6 и там останется (стационар).

Пример 2.

Здесь циклическое повторение событий.

На данном графе случайные блуждания из состояния в состояние.

Эргодичность может быть не по отношению ко всем узлам системы. Можно эргодическое поведение выделить в отдельную систему.

Пример. Составление ДУ Колмогорова

Система имеет размеченный граф. В начальный момент система находилась в состоянии S₁.

Написать над дугами обозначения интенсивностей, составить систему ДУ Колмогорова. Реализовать ее в среде MVS и найти финальные вероятности.

Граф после разметки

ДУ для состояния S₁:

Задание для самостоятельной работы.

Дописать систему ДУ Колмогорова.

Как найти финальные вероятности системы?

Вернемся к примеру состояний автомобиля (модель 8).

Мы выписали ДУ для вероятностей состояний исходя из здравого смысла. Но, зная уравнения Колмогорова, которые теоретически строго доказаны, мы видим, что полученная система уравнений соответствует этим уравнениям.

У нас записана система ДУ 1-го порядка, однородная с постоянными коэффициентами. Условие стационара для такой системы – равенство нулю правой части.

Это уравнения зависимые, т. к. в сумме дают 0.

Поэтому вместо одного используем равенство p₁+p₂=1, где p₁, p₂– финальные вероятности, т. е. система будет иметь вид:

Решив эту систему относительно p₁ и p₂, получим финальные вероятности системы:

Процессы гибели и размножения

Особый раздел теории — так называемые процессы гибели и размножения.

Встречается в разнообразных практических задачах.

Марковский процесс с дискретными состояниями S₀, S₁, S₂. S_n называется процессом гибели и размножения, если все состояния можно вытянуть в одну цепочку, в которой каждое из средних состояний (S₀, S₁, S₂. S_n) может переходить только в соседние состояния, которые, в свою очередь, переходят обратно, а крайние состояния (S₀, S_n) переходят только в соседние состояния (рис. 3).

Рис. 3. Граф состояний для процесса гибели и размножения

Название взято из биологических задач, где состояние популяции S_k означает наличие в ней k единиц особей.

Переход вправо связан с размножением единиц, а влево — с их гибелью.

У λ и μ индекс того состояния, из которого стрелка выходит.

С состоянием S_k связана неслучайная величина X_k: которая означает следующее: если система S в момент времени t находится в состоянии S_k, то дискретная случайная величина X(t), связанная с функционированием системы, принимает значение k. Таким образом, получаем случайный процесс X(t), который в случайные, заранее неизвестные моменты времени скачком изменяет свое состояние.

Марковским процессом гибели и размножения с непрерывным временем называется такой случайный процесс, который может принимать только целые неотрицательные значения. Изменения этого процесса могут происходить в любой момент времени, т. е. в любой момент времени он может либо увеличиться на единицу, либо уменьшиться на единицу, либо остаться неизменным.

В практике встречаются процессы чистого размножения и чистой гибели. Процессом чистого размножения называется такой процесс гибели и размножения, у которого интенсивности всех потоков гибели равны нулю; аналогично процессом чистой гибели называется такой процесс гибели и размножения, у которого интенсивности всех потоков размножения равны нулю.

Пример

Рассмотрим эксплуатацию компьютеров в вычислительном центре. Интенсивность приобретения новых компьютеров равна (t). Каждый поступивший компьютер списывается через случайное время Т_с. Срок службы компьютера Т_с распределен по показательному закону с параметром μ. Процесс эксплуатации компьютера является случайным процессом. А(t) – число компьютеров, находящихся в эксплуатации в момент t. Требуется вычислить вероятности P_i(t)=Р , если: 1) нет ограничений на число эксплуатируемых компьютеров, 2) может эксплуатироваться не более N компьютеров.

Пример

Процесс чистого размножения – производство товаров.

Видео:Вся теория вероятностей для экзамена за 20 минут. ЕГЭ профильный, Базовый, ОГЭСкачать

Статистическое моделирование экономических систем
(метод Монте-Карло)

Теоретические основы метода

Метод статистического моделирования (или метод Монте-Карло) – это способ исследования поведения вероятностных систем в условиях, когда неизвестны в полной мере внутренние взаимодействия в этих системах.

Метод основан на многократных испытаниях построенной вероятностной математической модели с последующей статистической обработкой полученных результатов.

Цель метода – определение числовых характеристик рассматриваемого процесса в виде статистических оценок его параметров.

Процесс моделирования функционирования экономической системы сводится к машинной имитации изучаемого процесса со всеми сопровождающими его случайностями.

Закон больших чисел

Основой метода статистического моделирования является закон больших чисел (ЗБЧ). ЗБЧ доказывает для различных условий сходимость по вероятности средних значений результатов большого числа наблюдений к некоторым постоянным величинам.

Практика изучения случайных явлений показывает, что хотя результаты отдельных наблюдений, даже проведенных в одинаковых условиях, могут сильно отличаться, в то же время средние результаты для достаточно большого числа наблюдений устойчивы и слабо зависят от результатов отдельных наблюдений.

Теоретическим обоснованием этого замечательного свойства случайных явлений является закон больших чисел. Названием «закон больших чисел» объединена группа теорем, устанавливающих устойчивость средних результатов большого количества случайных явлений и объясняющих причину этой устойчивости.

Центральная предельная теорема объясняет широкое распространение нормального закона распределения. Теорема утверждает, что всегда, когда случайная величина образуется в результате сложения большого числа независимых случайных величин с конечными дисперсиями, закон распределения этой случайной величины оказывается практически нормальным законом.

Предположим какой-то случайный процесс состоит из последовательности элементарных независимых процессов. Длительность каждого процесса t_i – является случайной величиной, распределенной по неизвестному закону с МО t_i и дисперсией . Допустим, что это непрерывное распределение, имеющее ограниченный (по абсолютной величине) третий момент. Тогда – случайная величина, являющаяся суммой n независимых случайных величин, распределенных по неизвестному закону и имеющих конечный третий момент.

Теорема (центральная предельная). Если сделать предельный переход, то распределение случайной величины t будет стремиться к нормальному с МО, равным сумме МО t_i и дисперсией, равной сумме дисперсий t_i

Рассматривается в различных математических постановках в литературе по теории вероятностей.

Пояснение. Практический смысл.

Любые сложные работы на объектах экономики (ввод информации их документа в компьютер, проведение переговоров, ремонт оборудования и пр.) состоят из множества коротких последовательных элементарных работ. Причем количество их велико, и требования теоремы можно считать выполняющимися. Поэтому при оценках трудозатрат всегда справедливо предположение о том, что их продолжительность – это случайная величина, распределенная по нормальному закону.

Предельная теорема о суперпозиции (наложении) потоков

Предположим, что можно наблюдать k независимых потоков событий. В каждом потоке можно наблюдать m_j элементарных событий. Интервалы между событиями – это независимые случайные величины, распределенные по неизвестному закону с МО . Если спроецировать на временную ось моменты наступления событий из наблюдаемых потоков, то получим случайные интервалы времени между событиями.

– случайный интервал между соседними событиями полученного суммарного потока.

Теорема. Если сделать предельный переход , то распределение случайной величины интервала t будет стремиться к показательному с МО, равным

Пример.

Имеется некая крупная фирма. Клиенты – физические и юридические лица. Каждый имеет свое расписание (набор планов и дел) на значительном интервале времени. Однако если рассмотреть суммарный поток обращений клиентов к служащим фирмы, то интервал между двумя последовательными обращениями будет случайной величиной, распределенной по экспоненциальному закону.

Примеры потоков, имеющих показательное (экспоненциальное) распределение:

• время поступления заказа на предприятие;
• посещение покупателями магазина;
• телефонные разговоры;
• срок службы деталей и узлов в компьютере.

Схема решения задачи методом статистического моделирования

1. Разработка и построение структурной схемы процесса, выявление основных взаимосвязей.
2. Формальное описание процесса.
3. Моделирование случайных явлений (случайных событий, случайных величин, случайных функций), сопровождающих функционирование исследуемой системы.
4. Моделирование функционирования системы – воспроизведение процесса в соответствии с разработанной структурной схемой и формальным описанием.
5. Накопление результатов моделирования, статистическая обработка, анализ и обобщение.

Результаты, получаемые при статистическом моделировании подвержены экспериментальным ошибкам.

Экспериментальные ошибки в значительной степени зависят от точности моделирования случайных явлений, сопровождающих функционирование системы. Моделирование случайных явлений сводится к моделированию случайных событий, случайных величин, случайных функций. Так как случайные события и случайные функции могут быть представлены через случайные величины, то моделирование случайных событий и случайных функций проводится с помощью случайных величин.

Видео:Теория вероятностей | Математика TutorOnlineСкачать

Моделирование случайных величин

Для моделирования случайной величины необходимо знать ее закон распределения.

Наиболее общим способом получения последовательности случайных чисел, распределенных по произвольному закону, является способ, основанный на формировании их из последовательности равномерно распределенных чисел на промежутке [0, 1].

Опишем этот способ более подробно на примере получения случайной величины с экспоненциальным распределением.

Экспоненциальное (показательное) распределение случайной величины задается плотностью распределения:

(мат.ожидание и среднеквадратическое отклонение равны 1/).

Существует связь между пуассоновским и экспоненциальным распределениями. Если случайная величина подчинена закону Пуассона и представляет собой число отказов в единицу времени, то случайная величина, которая определяет промежуток времени между двумя отказами, распределена по экспоненциальному закону. Чтобы получить величину этого интервала применяют следующий способ:

1. Генерируется случайное равномерно распределенное число ξ на промежутке [0,1]. В среде MVS это можно сделать с помощью функции uniform (0,1).
2. Для преобразования равномерно распределенного случайного числа в случайное число с заданным законом распределения F(t) надо решить уравнение вида. Если закон распределения задан плотностью распределения, то уравнение имеет вид.

Для показательного распределения уравнение имеет вид. Отсюда получаем величину , или поскольку выражение в скобках тоже равномерно распределенная случайная величина, то можно считать, что .

Такие же соотношения получены и для других законов распределения

Видео:Теория вероятностей #11: формула полной вероятности, формула БайесаСкачать

Уравнения Колмогорова.
Предельные вероятности состояний

Рассмотрим математическое описание марковского процесса с дискретными состояниями и непрерывным временем* на примере случайного процесса из примера 1, граф которого изображен на рис. 1. Будем полагать, что все переходы системы из состояния в происходят под воздействием простейших потоков событий с интенсивностями ; так, переход системы из состояния в будет происходить под воздействием потока отказов первого узла, а обратный переход из состояния в — под воздействием потока «окончаний ремонтов» первого узла и т.п.

Граф состояний системы с проставленными у стрелок интенсивностями будем называть размеченным (см. рис. 1). Рассматриваемая система имеет четыре возможных состояния: .

Вероятностью i-го состояния называется вероятность того, что в момент система будет находиться в состоянии . Очевидно, что для любого момента сумма вероятностей всех состояний равна единице:

Рассмотрим систему в момент и, задав малый промежуток , найдем вероятность того, что система в момент будет находиться в состоянии . Это достигается разными способами.

1. Система в момент с вероятностью находилась в состоянии , а за время не вышла из него.

Вывести систему из этого состояния (см. граф на рис. 1) можно суммарным простейшим потоком с интенсивностью , т.е. в соответствии с формулой (7), с вероятностью, приближенно равной . А вероятность того, что система не выйдет из состояния , равна . Вероятность того, что система будет находиться в состоянии по первому способу (т.е. того, что находилась в состоянии и не выйдет из него за время ), равна по теореме умножения вероятностей:

2. Система в момент с вероятностями (или ) находилась в состоянии или и за время перешла в состояние .

Потоком интенсивностью (или — с- рис. 1) система перейдет в состояние с вероятностью, приближенно равной (или ). Вероятность того, что система будет находиться в состоянии по этому способу, равна (или ).

Применяя теорему сложения вероятностей, получим

Переходя к пределу при (приближенные равенства, связанные с применением формулы (7), перейдут в точные), получим в левой части уравнения производную (обозначим ее для простоты ):

Получили дифференциальное уравнение первого порядка, т.е. уравнение, содержащее как саму неизвестную функцию, так и ее производную первого порядка.

Рассуждая аналогично для других состояний системы , можно получить систему дифференциальных уравнений Колмогорова для вероятностей состояний:

Сформулируем правило составления уравнений Колмогорова . В левой части каждого из них стоит производная вероятности i-го состояния. В правой части — сумма произведений вероятностей всех состояний (из которых идут стрелки в данное состояние) на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного (i-го состояния).

В системе (9) независимых уравнений на единицу меньше общего числа уравнений. Поэтому для решения системы необходимо добавить уравнение (8).

Особенность решения дифференциальных уравнений вообще состоит в том, что требуется задать так называемые начальные условия, т.е. в данном случае вероятности состояний системы в начальный момент . Так, например, систему уравнений (9) естественно решать при условии, что в начальный момент оба узла исправны и система находилась в состоянии , т.е. при начальных условиях .

Уравнения Колмогорова дают возможность найти все вероятности состояний как функции времени . Особый интерес представляют вероятности системы в предельном стационарном режиме , т.е. при , которые называются предельными (или финальными) вероятностями состояний.

В теории случайных процессов доказывается, что если число состояний системы конечно и из каждого из них можно (за конечное число шагов) перейти в любое другое состояние, то предельные вероятности существуют.

Предельная вероятность состояния имеет четкий смысл: она показывает среднее относительное время пребывания системы в этом состоянии . Например, если предельная вероятность состояния , т.е. , то это означает, что в среднем половину времени система находится в состоянии .

Так как предельные вероятности постоянны, то, заменяя в уравнениях Колмогорова их производные нулевыми значениями, получим систему линейных алгебраических уравнений, описывающих стационарный режим. Для системы с графом состояний, изображенном на рис. 1), такая система уравнений имеет вид:

Систему (10) можно составить непосредственно по размеченному графу состояний, если руководствоваться правилом , согласно которому слева в уравнениях стоит предельная вероятность данного состояния , умноженная на суммарную интенсивность всех потоков, ведущих из данного состояния, а справа — сумма произведений интенсивностей всех потоков, входящих в i-е состояние, на вероятности тех состояний, из которых эти потоки исходят.

Пример 2. Найти предельные вероятности для системы из примера 1, граф состояний которой приведен на рис. 1, при

Решение. Система алгебраических уравнений, описывающих стационарный режим для данной системы, имеет вид (10) или

(Здесь мы вместо одного «лишнего» уравнения системы (10) записали нормировочное условие (8)).

Решив систему (11), получим , т.е. в предельном, стационарном режиме система в среднем 40% времени будет находиться в состоянии (оба узла исправны), 20% — в состоянии (первый узел ремонтируется, второй работает), 27% — в состоянии (второй узел ремонтируется, первый работает) и 13% времени — в состоянии (оба узла ремонтируются)

Пример 3. Найти средний чистый доход от эксплуатации в стационарном режиме системы в условиях примеров 1 и 2, если известно, что в единицу времени исправная работа первого и второго узлов приносит доход соответственно в 10 и 6 ден.ед., а их ремонт требует затрат соответственно в 4 и 2 ден.ед. Оценить экономическую эффективность имеющейся возможности уменьшения вдвое среднего времени ремонта каждого из двух узлов, если при этом придется вдвое увеличить затраты на ремонт каждого узла (в единицу времени).

Решение. Из примера 2 следует, что в среднем первый узел исправно работает долю времени, равную , а второй узел — . В то же время первый узел находится в ремонте в среднем долю времени, равную , а второй узел — . Поэтому средний чистый доход в единицу времени от эксплуатации системы, т.е. разность между доходами и затратами, равен

Уменьшение вдвое среднего времени ремонта каждого из узлов в соответствии с (6) будет означать увеличение вдвое интенсивностей потока «окончаний ремонтов» каждого узла, т.е. теперь и система линейных алгебраических уравнений (10), описывающая стационарный режим системы , вместе с нормировочным условием (8) примет вид:

Решив систему, получим .

Учитывая, что , а затраты на ремонт первого и второго узла составляют теперь соответственно 8 и 4 ден.ед., вычислим средний чистый доход в единицу времени:

Так как больше (примерно на 20%), то экономическая целесообразность ускорения ремонтов узлов очевидна.

Видео:№3,4 Теория вероятностей из ЕГЭ по профильной математике | Интенсив "Щелчок"Скачать

Процесс гибели и размножения

В теории массового обслуживания широкое распространение имеет специальный класс случайных процессов — так называемый процесс гибели и размножения . Название этого процесса связано с рядом биологических задач, где он является математической моделью изменения численности биологических популяций.

Граф состояний процесса гибели и размножения имеет вид, показанный на рис. 4.

Рассмотрим упорядоченное множество состояний системы . Переходы могут осуществляться из любого состояния только в состояния с соседними номерами, т.е. из состояния возможны переходы только либо в состояние , либо в состояние .

Предположим, что все потоки событий, переводящие систему по стрелкам графа, простейшие с соответствующими интенсивностями или .

По графу, представленному на рис. 4, составим и решим алгебраические уравнения для предельных вероятностей состояний (их существование вытекает из возможности перехода из каждого состояния в каждое другое и конечности числа состояний).

В соответствии с правилом составления таких уравнений (см. 13) получим: для состояния

для состояния имеем , которое с учетом (12) приводится к виду

Аналогично, записывая уравнения для предельных вероятностей других состояний, можно получить следующую систему уравнений:

к которой добавляется нормировочное условие

При анализе численности популяций считают, что состояние соответствует численности популяции, равной , и переход системы из состояния в состояние происходит при рождении одного члена популяции, а переход в состояние — при гибели одного члена популяции.

Решая систему (14), (15), можно получить

Легко заметить, что в формулах (17) для коэффициенты при есть слагаемые, стоящие после единицы в формуле (16). Числители этих коэффициентов представляют произведение всех интенсивностей, стоящих у стрелок, ведущих слева направо до данного состояния , а знаменатели — произведение всех интенсивностей, стоящих у стрелок, ведущих справа налево до состояния .

Пример 4. Процесс гибели и размножения представлен графом (рис. 5). Найти предельные вероятности состояний.

📸 Видео

Математика без Ху!ни. Теория вероятностей, комбинаторная вероятность.Скачать

Теория вероятностей в профильном ЕГЭ 2022. Задача 10Скачать

Предельные вероятности состоянийСкачать

Функция распределения непрерывной случайной величины. Вероятность попадания в интервалСкачать

Теория вероятностей на пальцахСкачать

Теория вероятностей, задача с круглым столомСкачать

Теория вероятности 🔥 А полезный файлик в комментариях #математика #огэ #огэматематикаСкачать

Теория вероятностей #3: зависимые/независимые события, условная вероятность, их произведение.Скачать

Теория вероятностей #14: математ. ожидание, дисперсия, медиана, мода, начальные моментыСкачать

Вся суть теории вероятностей — за 900 секунд!Скачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

ТЕОРИЯ ВЕРОЯТНОСТИ НА ЭКЗАМЕНЕ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать